矩形截面空腹桁架拱平面外稳定性研究
荆 斓 石敏洁
(1.中铁建设集团有限公司 北京 100040;2.贵州大学空间结构研究中心 贵州贵阳 550025)
1 引言
与传统的桁架拱相比,空腹桁架拱外观更为简洁,透光性能更为良好,因此广泛应用于大跨结构中,如体育馆、展览馆和火车站等。与单一的平面内弯曲失稳不同,对于无支撑或支撑数量不足的钢拱,在承载过程中,钢拱可能会发生平面外弯曲-扭转失稳,因此,钢拱的平面外失稳问题较平面内更加复杂。自1961年,Timoshenko等[1]提出实腹式拱的平面外弹性屈曲荷载解之后,国内外一些学者针对拱的平面外稳定问题相继进行了研究。
Pi等[2]建立了钢拱的面外弯扭屈曲能量方程,得到纯压开口薄壁钢拱的弹性屈曲荷载。杨永华、窦超[3-5]等人采用平衡法确立单轴对称和双轴对称截面钢拱的平面外弹性屈曲荷载理论。Dou等[6]采用平衡法得到纯压、纯弯拱的面外弹性屈曲荷载解。Pi等[7-9]系统地研究了工形截面在各种荷载情况下的屈曲后性能及稳定承载性能。乔彩虹和郭彦林[10]建议对于钢拱的平面外稳定性可以采用正则化长细比进行验算。赵思远等[11-13]讨论了桁架拱和闭合截面钢拱的平面外稳定性能,分别建立了不同钢拱的平面外弹塑性稳定设计方法。王青蕊[14]研究了钢筋混凝土系杆拱桥在整个施工阶段位移和应力情况,发现系梁最大压应力出现在截面突变处,拱肋最大应力出现在1/8截面处。
然而,关于空腹桁架拱的平面外弹塑性稳定承载力的研究,目前尚未发现相关文献报道,其平面外失稳机理和设计方法尚不明晰。因此本文采用理论与数值模拟相结合的方法,对矩形截面空腹钢管桁架拱在全跨均布径向荷载、全跨均布竖向荷载和半跨均布竖向荷载作用下的平面外失稳机理和整体弹塑性稳定性能进行深入地研究,并提出相关的稳定承载力设计方程以供实际工程参考。
2 有限元模型
本文以矩形截面空腹钢管桁架拱为研究对象,其结构形式如图1所示,结构杆件均采用圆钢管。运用有限元软件进行模拟分析,选取梁单元beam189建立计算模型。图中,f为拱的矢高,L为跨度,S为拱弧全长,R为半径,Θ为圆心角,B和H分别为矩形桁架截面的宽和高,Lc为相邻腹杆轴线间的距离,即节间长度;Dc和tc为弦杆横截面的外径和壁厚,Dt和tt为腹杆横截面的外径和壁厚。
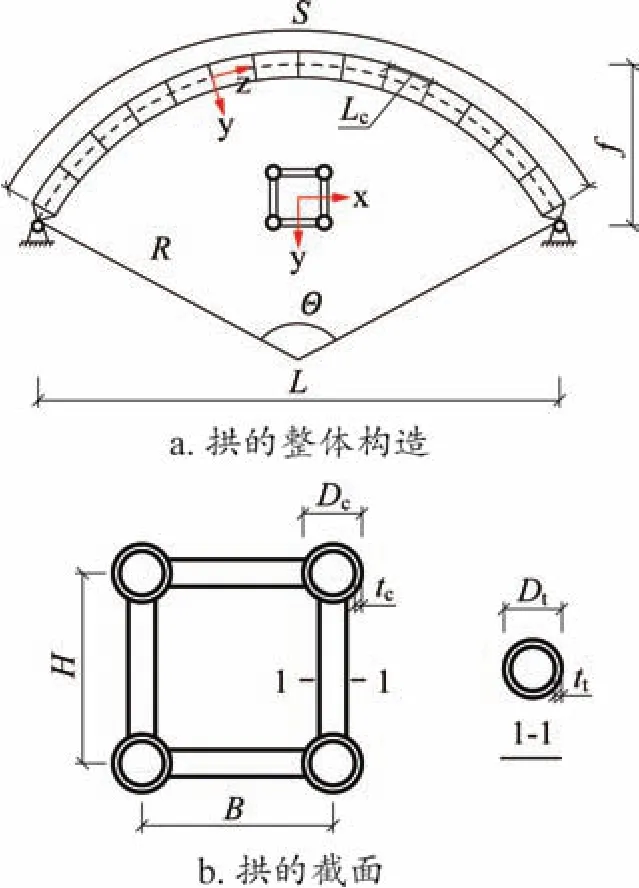
图1 矩形截面空腹钢管桁架拱
在进行空腹桁架拱的内力分析时,根据文献[15],为了得到拱的内力值,在进行空腹桁架拱的内力分析时,可以将矩形空腹桁架拱等效为矩形截面实腹式拱,二者具有相同截面面积和惯性矩,建立等效模型进行内力分析。等效的有限元模型仅用于分析拱的弹性内力和相应的变形。拱脚采用销轴支座,在有限元模型中,将空腹桁架拱两端的弦杆稍伸出并相交于一点,在此点施加边界约束:约束两端拱脚的平面外转动自由度、绕拱轴切向扭转的自由度以及沿三个主轴方向的平移,而平面内可以自由转动。
本文采用理想弹塑性材料模型,弹性模量E=206 GPa,弦杆屈服强度fyc=235 MPa,腹杆屈服强度fyt=345 MPa。考虑到平面外初始几何缺陷对拱的弯扭屈曲荷载影响较大,因此按照一致模态缺陷法在模型中引入面外初始几何缺陷,缺陷幅值统一取为S/1 000。文中考虑的荷载工况主要有:全跨均布径向荷载,全跨均布竖向荷载和半跨均布竖向荷载。
3 平面外整体弹性屈曲
3.1 剪切刚度
矩形截面空腹桁架拱的剪切机理与四肢缀板格构柱相似,截面的剪切变形对结构稳定性的影响不容忽视。从较短的拱轴线长度范围内取出一个节间以分析剪力作用下拱的变形,并假设反弯点位于弦杆节间段的中点。
在任意剪力V作用下,上、下弦杆均匀承担截面剪力,弦杆和腹杆共同承担剪力产生的弯矩。空腹桁架拱的剪切变形分为两部分:分别是弦杆弯曲和直腹杆弯曲产生的侧向变形δ1和侧向变形δ2,计算式如下:

得桁架拱的剪切角为:

因此,矩形空腹桁架拱的平面外剪切刚度为:

式中,Ic为弦杆截面惯性矩;It为腹杆截面惯性矩。
3.2 自由扭转刚度
在计算截面抗扭刚度时,由于空腹桁架拱为格构式截面,因此可折算为矩形薄壁闭合构件,即截面由4块具有一定厚度的薄板组成,按照薄壁闭合截面计算扭转刚度[16]。
取一个节间长度Lc为计算单元,根据扭转应变能相等原则,可得各边薄板的厚度为:

式中,li为各边的长度;G为材料的剪切模量,且G=E/2.6。
得截面的扭转刚度为:

式中,A0为薄壁矩形中心线围成的面积。
3.3 平面外弹性屈曲荷载
在全跨均布径向荷载作用下,拱处于均匀受压状态,确定其平面外弹性屈曲荷载计算公式是进行弹塑性稳定设计的基础。在平面外屈曲分析中,销轴支座拱与固支拱并无实质性区别,因此,为便于实际工程的应用,以两端嵌固实腹式拱的面外屈曲理论为基础,同时考虑剪切变形的影响,采用数值拟合的方法获得拱在均匀压力下的平面外弹性屈曲荷载:
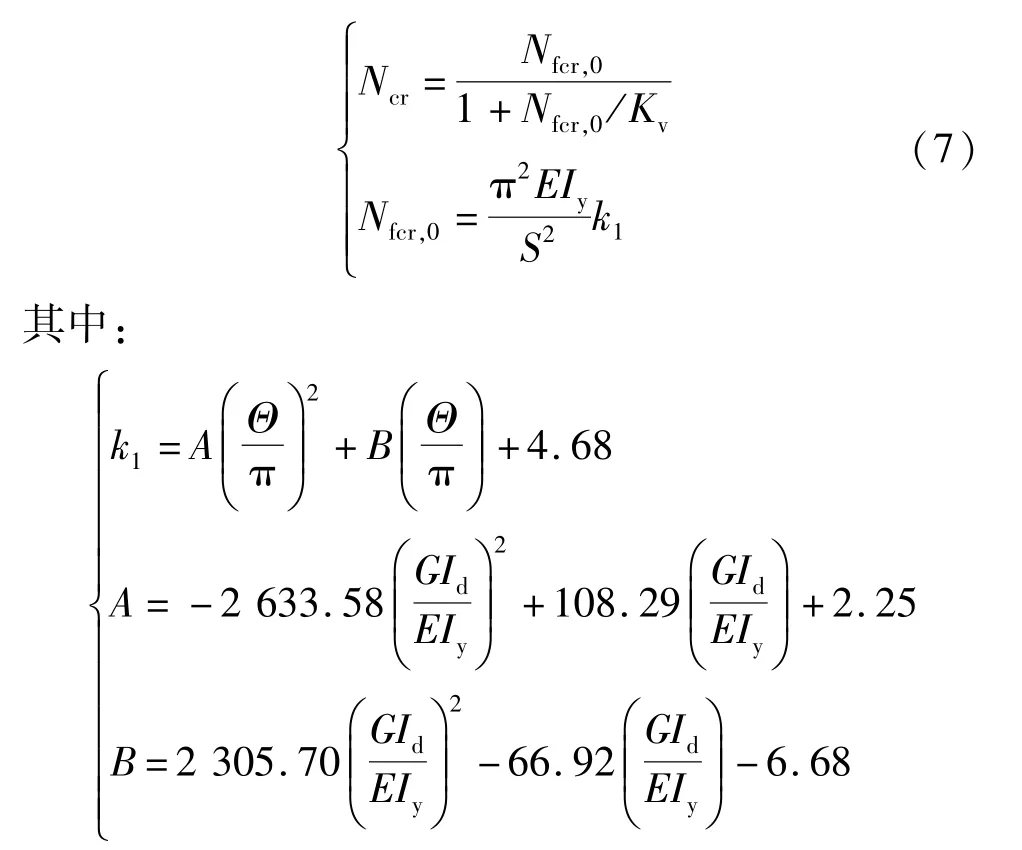
式中,EIy为截面的面外抗弯刚度,EIy=EAcB2。
为验证公式(7)的正确性,建立有限元模型并进行平面外屈曲分析。模型参数为:Dc×tc=0.121×0.01 m,Dt×tt=0.1×0.01 m,B=H=Lc=0.5 m,变化结构的跨度和矢跨比,有限元结果与公式(7)的对比如图2所示。
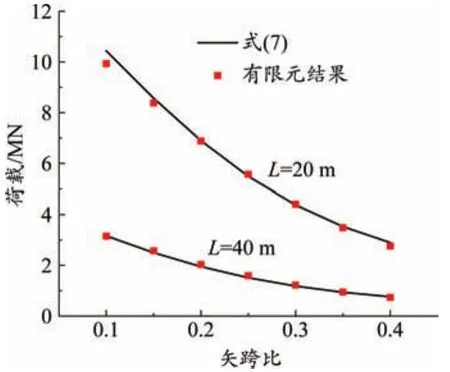
图2 式(7)与有限元结果的比较
由图2可知,保持其他参数不变,仅增大结构的跨度或矢跨比,可以看到桁架拱的平面外屈曲荷载也随之减小。数据显示,公式计算结果与有限元结果的最大误差不超过8%,表明两者具有良好的一致性。
4 平面外整体弹塑性稳定设计
4.1 全跨均布径向荷载作用
空腹桁架拱在全跨均布径向荷载作用下处于均匀受压状态,由弦杆承担所有轴力,为避免弦杆先于结构整体失去承载能力,应限制弦杆的长细比以避免弦杆先于结构整体失去承载能力,参考《钢结构设计规范》,弦杆长细比限制条件为:

式中,λoy为拱截面绕y轴的换算长细比,定义如下:

式中,λc为弦杆长细比,由式(10)计算;λy为结构整体的面外几何长细比;由式(11)计算。ib为同一截面处腹杆线刚度之和;ic为弦杆的线刚度;本节建立的有限元模型均需满足长细比限值条件。
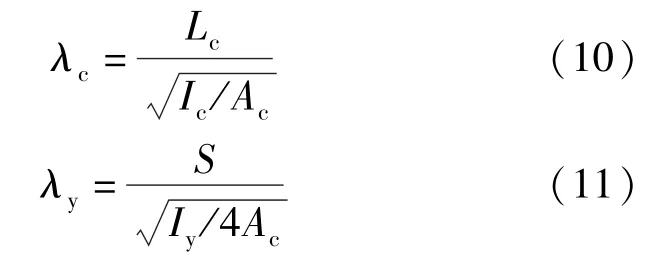
通过建立有限元模型进行弹塑性全过程分析,以了解矩形空腹桁架拱在均匀压力作用下的平面外整体失稳过程及破坏机理。模型的尺寸为:f/L=0.3,L=20 m,B=H=0.5 m,Lc=B,Dc×tc=0.121×0.01 m,Dt×tt=0.1×0.01 m,λc=19。拱顶处的荷载-位移曲线如图3所示。

图3 拱顶的荷载位移曲线
由图3可知,随着荷载的增加,拱顶处的平面外位移随之增大,当到达拱的极限承载力后,位移持续增大,而荷载逐渐减小。拱的变形在荷载作用下进一步扩展,由于存在平面外初始几何缺陷,拱截面会产生附加弯矩,弦杆同时承受轴压力和弯矩,因此最先到达屈服强度。随着荷载的增加,屈服区域逐渐发展直至达到拱的极限承载力,1/4和3/4跨处的弦杆完全屈服,之后,位移继续增大,直至桁架拱发生整体失稳破坏。在加载期间,腹杆始终保持弹性状态[17]。
引入正则化长细比以研究均匀受压桁架拱的稳定承载力。正则化长细比和稳定系数的定义如下:
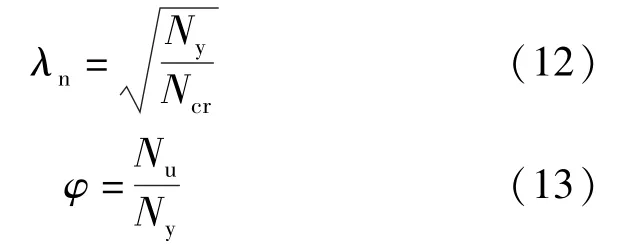
式中,Ncr为空腹桁架拱的平面外弹性屈曲荷载,按照式(7)计算;Ny为拱截面的塑性轴力,按照式(14)计算;Nu为均匀受压空腹桁架拱的极限荷载,通过有限元计算得到。

建立有限元模型进行非线性弹塑性分析,模型参数为:f/L=0.1~0.4,L=20~60 m,B=H=0.5 m,Lc=B和Lc=1.5B,Dc×tc=0.121×0.01 m,Dt×tt=0.1×0.01 m,弦杆长细比满足式(8)的限制条件。根据公式(12)和(13),并结合有限元分析结果,可得正则化长细比与稳定系数的关系曲线,如图4所示。图中也给出了《钢结构设计规范》中的a~c类柱子稳定曲线。

图4 纯压空腹桁架拱的稳定曲线
由图4可知,有限元计算结果均位于a类柱子曲线上,表明矩形截面空腹桁架拱在全跨均布径向荷载作用下处于均匀受压状态,因此可以根据《钢结构设计规范》(GB 50017—2017)中的a类柱子稳定曲线进行纯压拱的稳定承载力设计,其设计公式为:

4.2 整体稳定承载力设计
当空腹桁架拱的节间长度较小时,拱更易发生整体破坏,原因在于剪力在节间弦杆两端产生的弯矩较小。为研究矩形空腹桁架拱在压弯状态下的整体破坏模式,以全跨均布竖向荷载工况为例,进行有限元分析,模型参数为:f/L=0.3,L=40 m,B=H=0.5 m,Lc=B或Lc=1.5B,Dc×tc=0.121×0.01 m,Dt×tt=0.1×0.01 m,拱顶处的荷载-位移曲线如图5所示。

图5 拱顶的荷载位移曲线
由图5可知,当其他参数保持不变时,增大节间长度,拱的极限荷载随之降低,这是因为节间长度的增加会使拱的剪切刚度减小,最终会降低拱的极限荷载。拱的1/4跨处的下弦杆在轴力和弯矩的共同作用下,最先进入屈服。荷载继续增加,塑性区域逐渐扩大,并向拱脚扩展,当到达极限承载力后,拱表现为塑性破坏。
由于格构式截面存在较大的剪切变形,其造成的影响不容忽视,因此引入弯矩放大系数α以考虑二阶弯矩对矩形空腹桁架拱承载力的影响。在压弯荷载作用下,矩形空腹钢管桁架拱的整体稳定设计公式为:

式中,N为极限荷载作用下的轴力,由于拱内各段轴力分布不均匀,故N取最小轴力与最大轴力的平均值,M为极限荷载作用下的弯矩,M取最大值;φ为均匀压力作用下矩形空腹桁架拱的平面外稳定系数,可按照GB 50017—2017的a类柱子曲线获得;M为弦杆全截面塑性轴力,按照式(14)计算;My为塑性弯矩,且My=NyB/2;α为弯矩放大系数,且α≤1.4,其表达式见式(17)。

式中,Ncr为纯压矩形空腹桁架拱的平面外弹性屈曲荷载,由式(7)得到。若α>1.4,则需进行二阶弹性分析以获得最大弯矩αM。
采用有限元算例验证公式(16)能否用于计算矩形截面空腹桁架拱的平面外整体承载力,模型参数为:f/L=0.1~0.4,L=20~60 m,B=H=0.5 m,Lc=B和Lc=1.5B,Dt×tc=0.121×0.01 m,Dt×tt=0.1×0.01 m,有限元结果与公式(16)的比较如图6所示。
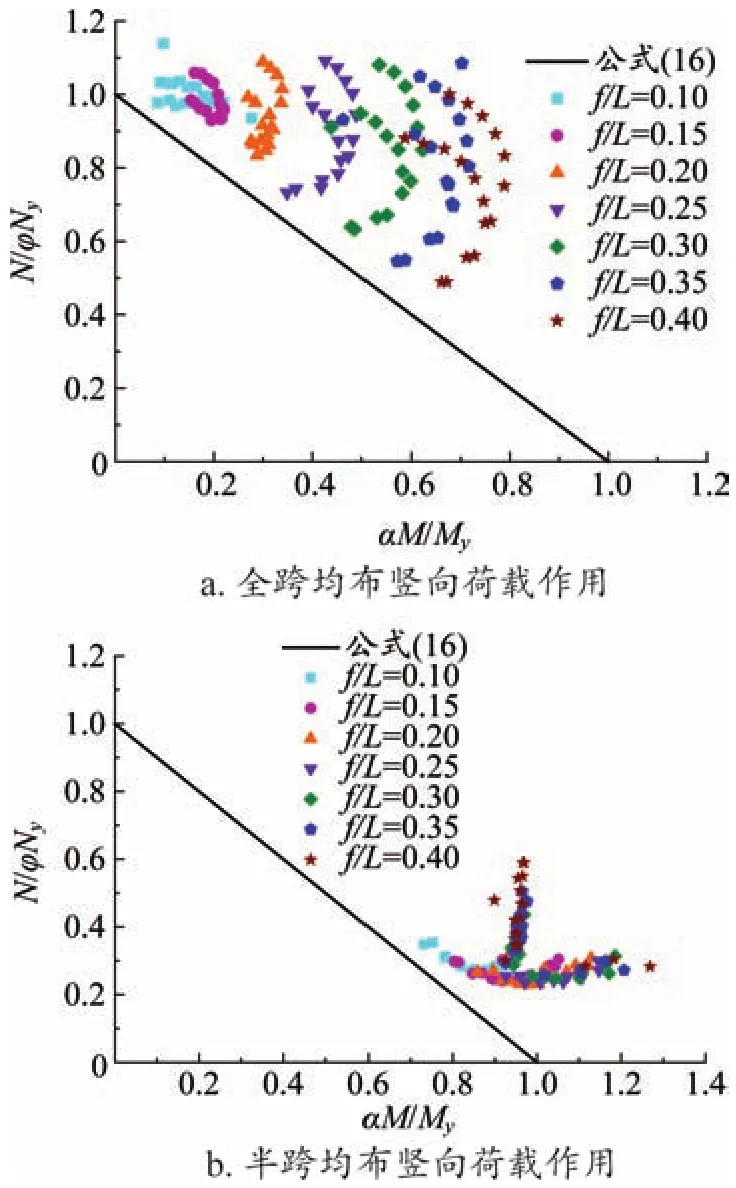
图6 公式(16)与有限元结果对比
由图6可知,拱在全跨荷载作用下发生整体破坏时,随着矢跨比的增加,弯矩所占比重逐渐增大;在半跨荷载作用下,计算结果都集中在坐标系的右下方,表明拱发生平面外整体破坏时,弯矩为主要影响因素,而轴压力为次要因素;两种荷载下的所有数值结果均位于设计曲线上方,表明可以采用公式(16)来保守估计矩形截面空腹桁架拱在压弯状态下的平面外整体稳定承载力。
5 结论
本文研究了矩形截面空腹钢管桁架拱的平面外稳定承载性能,所得结论如下:
(1)空腹桁架拱在均布径向荷载作用下处于均匀受压状态,通过引入正则化长细比,建立纯压拱的弹塑性平面外整体破坏设计公式。有限元计算结果表明,可采用《钢结构设计规范》(GB 50017—2017)中的a类柱子稳定曲线进行纯压拱的平面外整体稳定设计。
(2)在均匀压力或压弯作用下,弦杆作为主要的受力构件,既承受轴力同时也承受弯矩,因此纯压拱和压弯拱的整体破坏模式类似,都表现为1/4或3/4跨处的弦杆先屈服,位移继续增大,直至桁架拱发生整体弹塑性破坏。
(3)空腹桁架拱在全跨均布竖向荷载和半跨均布竖向荷载作用下均会发生平面外整体压弯破坏,提出的压弯稳定设计公式(16)对估计以上两种荷载工况下拱的承载力均适用。

