工业燃气锅炉使用过程中煤炭使用量预测方法

石 磊

(辛集市建投燃气有限公司，河北 辛集 052300)

在人类的发展中，能源一直处于极其重要的地位。只有实现能源安全，才能实现经济的稳定、持续、高效发展。在改革开放后，我国经济发展速度惊人，大幅改善了我国人民的生活[1]。而经济的高速、持续发展带来了能源消耗量的大幅增加。煤炭在我国一直是主要能源，煤炭消耗量在我国整体能源消耗量中一直占据很大占比。随着煤炭消耗量逐年攀升，其引发的环境问题也越来越严重[2]。可以说，煤炭消耗量的增加对于环境一直是一种巨大的压力，也已经成为社会环境保护、经济发展的瓶颈，在煤炭能源的使用中实现节能降耗早已是环境领域中一个重要的议题。

我国区域经济发展与整体煤炭分布不匹配，并且缺乏良好的煤炭运输能力，使燃煤电厂使用的煤种十分混杂，导致工业燃气锅炉使用过程中煤炭使用量与设计值有着较大偏离[3]。同时各地煤炭使用量的相关指标有着很大差异，包括灰熔融性、灰分、硫分、挥发分、发热量以及煤炭类别等，也间接导致了煤炭使用量与设计值的偏离问题。该问题会引发一系列更深层次的问题，包括引风系统、送风系统、制粉系统等锅炉辅助机组设备容易出现出力不足的问题，对锅炉出力造成严重影响；炉膛结渣，使技改工程与检修费用上升；增加环保压力。因此，对工业燃气锅炉使用过程中煤炭使用量预测问题进行研究。很多国家在工业燃气锅炉中都使用混煤，因此很早就开始对该问题进行研究，特别是一些煤炭硫分不均以及煤炭资源匮乏的国家。研究发现煤炭使用量预测与煤炭品质、混煤比例、氧浓度等因素相关，具体需要根据各国混煤情况来预测。在研究中应用了热分析技术、神经网络算法、模糊算法等，取得了一定研究成果。现综合以往取得的研究成果，针对我国国情设计一种工业燃气锅炉使用过程中煤炭使用量预测方法。

1 煤炭使用量预测方法设计

为实现工业燃气锅炉使用过程中，对煤炭使用量进行有效预测，先通过Simulink仿真工具构建工业燃气锅炉仿真模型，然后对原始煤炭使用量数据进行降噪处理，获取数据的波动成分与趋势成分时间序列，最后使用ARMA时间序列法构建煤炭使用量预测模型，完成工业燃气锅炉使用过程中煤炭使用量预测方法的设计。

1.1 构建工业燃气锅炉仿真模型

时间变化下焦化、烧结等工序实际用煤量的变化规律仿真，构建工业燃气锅炉仿真模型。在仿真模型的创建中，使用的仿真工具为Simulink，该工具可实现仿真的可视化，通过其图形用户接口即可对模型方块图进行构建，仅需拖动鼠标和单机操作即可完成[4]。为实现模型的动态展示，模型的建模展现形式为框图形式。随着实际情况的变化，各模块也会产生变化，以实现模型的补充、修改以及添加等操作。工业燃气锅炉Simulink仿真模型如图1所示。

通过分层设计方式创建该仿真模型，模型的最高层是工业燃气锅炉整体模型，下一层为锅炉的子模型，而子模型中包括下一个层次的对应子模型，一直到最底层。各个子模型均有其确定的运行功能和物理意义[5]。共构建10个一级子模型，分别为LDG动态调度模型、COG动态调度模型、BFG动态调度模型、稳定富余量分配优化模型、LDG主工序消耗模型、LDG产生模型、COG主工序消耗模型、COG产生模型、BFG主工序消耗以及BFG产生模型。模型总层数为4级，子模型总数量为106个。

以BFG产生模型一级子模型为例，对其子模型构造进行详细介绍。该模型中的子模型包括高炉煤气计算子模型、发生量显示子模型以及多个高炉对应的BFG二级子模型[6]。其中多个高炉对应的BFG二级子模型中包含的子模型为处理煤气发生量与输入脉冲信号的子模型、序列输入子模型、增长子模型、斜坡函数子模型、矩形波发生子模型、标量转换子模型、类型判断与函数关系选择与计算子模型、输入时间序列子模型、输入工况序列子模型。通过以上三级子模型，能够获取高炉BFG产生量的动态变化曲线与大小。

1.2 构建煤炭使用量预测的ARMA时间序列模型

1.2.1 ARMA时间序列模型构建

使用ARMA时间序列法实施工业燃气锅炉使用过程中煤炭使用量的预测，构建ARMA时间序列模型。ARMA时间序列模型的建模分为4步：第1步为序列分析，第2步为模型识别，第3步为参数估计，第4步为模型检验[7]。

(1)通过序列分析能够对时间序列是否满足模型构建条件进行判断，以及判断是否需要进一步处理序列，如进行序列差分处理等。当工业燃气锅炉使用过程中原始煤炭使用量数据时间序列{Yt}={y1，y2，…，yt}满足以下条件：①对于任意时间t，时间序列的均值永远是常数；②对于2个任意时间，其自相关系数仅与两者时间间隔有关[8]。则可称该原始煤炭使用量数据时间序列为平稳时间序列。利用自相关分析图可以对序列平稳性进行判断。当其不够平稳，需要进行建模前的数据处理，使其平稳性满足条件[9]。

(2)通过模型识别能够分析原始煤炭使用量数据时间序列中的偏自相关函数与自相关函数，对使用的ARMA时间序列模型进行确定[10]。ARMA时间序列模型共有3种：MA(q)、ARMA(p，q)、AR(p)。其中，MA(q)时间序列模型的偏自相关函数具体见式(1)：

yt=ut-θ1ut-1-θ2ut-2-…-θqut-q

(1)

式中，θq为第q个模型自相关阈值；ut-q为第q个模型偏自相关阈值。

MA(q)的自相关函数具体见式(2)：

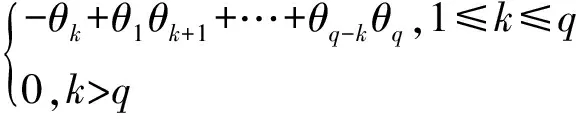
(2)

式中，k为滞后期。

对于MA(q)时间序列模型来说，其偏自相关函数伴随着q的增加表现出指数衰减或正弦波衰减倾向，具有拖尾性；而当k>q后其自相关函数的值一直为0，具有截尾性。对于ARMA(p，q)来说，2种函数均具有拖尾性。对于AR(p)时间序列模型来说，其两种函数的性质与MA(q)相反[11]。以原始煤炭使用量数据时间序列中的偏自相关函数与自相关函数性质为依据对ARMA时间序列模型进行选择，并进行模型定阶。

(3)模型定阶后通过软件实施参数估计。

(4)检验模型合适性，也就是对残差序列MA(q)实施白噪声检验。未通过检验时，需要进一步改进模型。

在检验中，通常侧重于检验随机性，也就是k≥1时，et的自相关系数应与0 相近[12]。随机性的检验中，使用χ2检验法，将et之间的相互独立作为检验的零假设。et的自相关函数具体见式(3)：

(3)

式中，rk(e)为et的自相关函数；n为序列观测值；m为最大滞后期。

et的检验统计量为：

(4)

对于不通过检验的情况，需要通过ARCH模型提取残差内的有用信息[13]。

1.2.2 数据处理

直接采用工业燃气锅炉使用过程中的原始煤炭使用量数据进行预测，会使预测性能受到数据噪声影响，使得预测精度受到影响。因此将原始数据分成2部分：波动成分与长期趋势。如何对原始序列进行分解成为关键问题，选用的方法为HP(Hodrick-Prescott)滤波法，以滤波序列为依据对稳定成分进行提取[14]。获取波动成分序列与长期趋势序列，并解决样本末端问题。

将Yt设为原始煤炭使用量数据时间序列，将其分解为长期趋势变动要素gt和周期变动要素ct，这里2种要素为不可观测的数值，则下式成立：

Yt=gt+ct，t=1，2，…，T

(5)

式中，t为原始煤炭使用量数据序列个数也就是时间序列中的时间；T为原始煤炭使用量数据序列最大个数。设序列平滑参数为λ，L为gt的延迟算子。可得出原时间序列的趋势循环分量B：

(6)

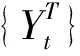
(7)

式中，γ为滤波最小化阈值；c(L)为延迟算子多项式，计算公式具体如下：

c(L)=(L-1-1)-(1-L)

(8)

则滤波问题可转化为最小损失函数问题，S为损失函数。具体为：

(9)

对于λ的取值，选择经验值10，完成趋势成分的分离后即可获得波动成分[15]。

通过以上数据处理过程，即可获取工业燃气锅炉使用过程中原始煤炭使用量数据的波动成分与趋势成分时间序列[16]。在此煤炭使用量预测的ARMA时间序列模型中输入以上2种时间序列，通能够使模型的预测性能不会受到数据噪声影响，从而提高预测精度。实现工业燃气锅炉使用过程中煤炭使用量的有效预测。

2 实例分析

2.1 高炉煤炭使用量预测实验

煤炭资源的开发为国家和地区带来了较大的经济效益，但是同时煤炭的过分使用也为当前生态环境带来了巨大的负担。因此通过对工业燃气锅炉使用过程中煤炭使用量进行预测，才能够实现经济的稳定、持续、高效发展。本文通过实例分析，对设计的工业燃气锅炉使用过程中煤炭使用量预测方法进行性能考核。以某市某钢铁企业的高炉以及焦炉为实验对象，分别实施工业燃气锅炉使用过程中煤炭使用量的预测实验。

此次实验选取高炉2个、焦炉2个，分别标号为高炉1、高炉2、焦炉1和焦炉2。实验对象现场如图2所示。

图2 实验高炉与焦炉现场Fig.2 Field diagram of experimental blast furnace and coke oven

对于该企业的高炉煤炭使用量预测实验，在预测前首先构建2个高炉的仿真模型，并实施2高炉使用过程中煤炭使用量原始时间序列数据的滤波处理，获取原始时间序列数据的波动成分与趋势成分，其处理结果具体如图3所示。

图3 高炉煤炭的滤波处理结果Fig.3 Filter processing results of blast furnace coal

使用原始煤炭使用量数据的波动成分与趋势成分时间序列进行煤炭使用量预测，预测结果具体见表1。

根据表1高炉煤炭使用量的预测结果，2个高炉在不同时间段的预测值都比较准确，与实际值较为贴近，整体平均绝对误差低于1.2%。说明设计的工业燃气锅炉使用过程中煤炭使用量预测方法具有良好的高炉煤炭使用量预测性能。

表1 高炉煤炭使用量预测结果Tab.1 Forecast results of coal consumption in blast furnace

2.2 焦炉煤炭使用量预测实验

在煤炭使用量预测实验中，共对2个焦炉300 h内的煤炭使用量进行预测。在预测前首先构建2个焦炉的仿真模型，并实施焦炉使用过程中煤炭使用量原始时间序列数据的滤波处理，获取原始时间序列数据的波动成分与趋势成分，其处理结果具体如图4所示。

图4 焦炉煤炭的滤波处理结果Fig.4 Filter processing results of coke oven coal

使用图4中的滤波处理数据进行煤炭使用量预测，预测结果具体见表2。由表2可知，2个焦炉在不同时间段的预测值都与实际值贴近，较为准确，整体平均绝对误差低于0.7%。说明设计方法具有良好的焦炉煤炭使用量预测性能。

2.3 转炉煤炭使用量预测实验

实验钢铁企业共有2种转炉，一种是顶吹转炉A，另一种是顶底复吹转炉B，如图5所示。分别对2种转炉进行煤炭使用量预测实验。

表2 焦炉煤炭使用量预测结果Tab.2 Forecast results of coal consumption in coke ovens

图5 顶吹转炉与顶底复吹转炉现场Fig.5 Site drawing of top blown converter and top bottom combined blown converter

在预测前，首先构建2种转炉的仿真模型，并实施2种转炉使用过程中煤炭使用量原始时间序列数据的滤波处理，获取原始时间序列数据的波动成分与趋势成分，其处理结果具体如图6所示。使用图6中的滤波处理数据进行2种转炉的煤炭使用量预测实验，实验结果具体如图7所示。由图7可知，2种转炉煤炭使用量预测结果与实际结果的差异都不大，整体预测比较准确，说明本文设计方法具有良好的转炉煤炭使用量预测性能，可以满足实际工业生产需要。

3 结语

在对工业燃气锅炉使用过程中煤炭使用量预测问题进行研究的过程中，构建了煤炭使用量预测模型，实现了各种煤炭燃气锅炉使用量较为准确地预测。并通过在某钢铁企业的高炉、焦炉和转炉的预测实验，证明了该方法的有效性与实际应用性能。由于研究尚不够深入，本文预测的准确性仍有提升空间，后续将进行更加深入的研究。

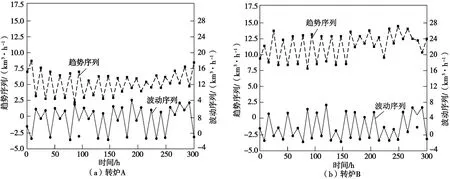
图6 转炉煤炭的滤波处理结果Fig.6 Filter processing results of converter coal

图7 两种转炉煤炭使用量预测实验结果Fig.7 Two kinds of converter coal consumption prediction experimental results