自然循环废液蒸发器液位测量分析及仿真

高永新，付 豪

(中国核电工程有限公司，北京 100840)

0 引言

在核电厂废液处理系统中，废液蒸发器是重要的工艺设备。核电厂废液蒸发器采用自然循环外加热式蒸发器。蒸发器液位通过连锁进料阀进行自动调节控制，使蒸发器液位保持在目标液位。蒸发器液位的平稳控制在废液蒸发处理时起关键作用。液位过高时，会因蒸汽带液影响汽水分离；液位过低时，会影响蒸汽和废液的自然循环，对系统稳定运行造成影响[1]。因此，保证蒸发器液位测量的准确、可靠非常重要。

1 废液蒸发器简介

废液蒸发器为外加热自然循环式，由加热器和蒸发器组成。加热器分为管程和壳程。加热器管程内，废液通过蒸汽加热至沸腾汽化，使汽液混合的废液密度显著降低，在加热器和蒸发器之间形成不平衡静压差，从而获得向上的推动力，再由加热器上出口流入蒸发器。废液在重度差的作用下循环蒸发。蒸汽流量越大，获得的推动力越强，循环速度越快[2]。由蒸发器顶部管道排出废液蒸发产生的二次蒸汽，由蒸发器底部管道补充废液，使液位达到动态平衡。正常运行时，蒸发量约为3.85 t/h。待废液中不可蒸发物浓度达到一定指标，再将废液全部排空。废液具有温度高、放射性高、化学物质多等特点。废液蒸发器如图1所示。

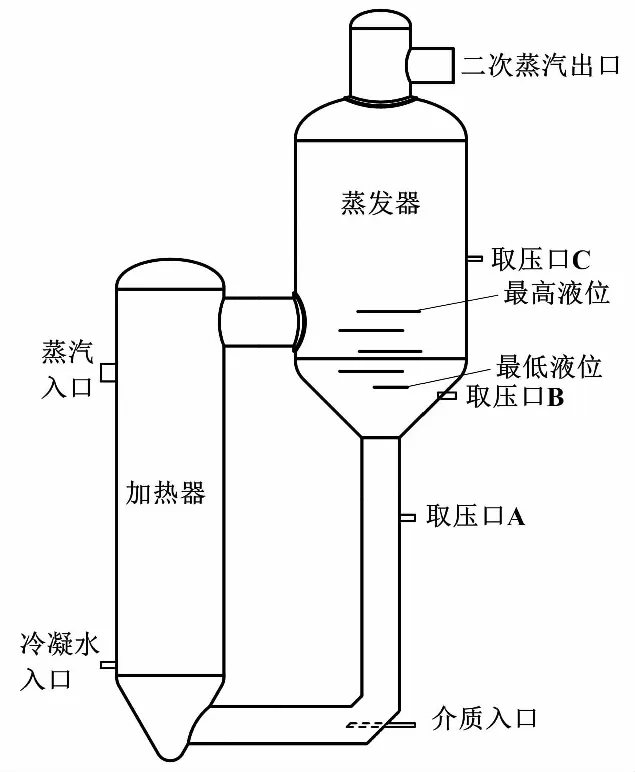
图1 废液蒸发器示意图

2 蒸发器液位测量

根据废液介质特性及测量条件，废液蒸发器液位测量选用差压式液位计。依据液体压强公式，通过测量蒸发器内液体侧与气体侧的压强差，计算得出蒸发器液位。废液中含有较多的化学物质。随着水分的蒸发，废液密度不断上升。如果仅用一个固定值来代表废液密度，液位计算值会有较大偏差。因此，需要连续监测废液密度，以提高液位测量精度，并减小密度变化带来的液位计算值偏差。另外，废液密度测量也用于辅助判断废液浓缩程度。

2.1 废液密度测量

废液密度一般为1.0～1.4 g/cm3。废液密度的测量同样采用差压法。依据液体压强公式，通过测量蒸发器内液体侧不同高度的两点压强差，计算得出蒸发器废液密度。

2.2 安装和计算方法

差压变送器的测量原理是：将来自引压管中的压力作用于传感器测量元件上；测量元件将测得的压差值转换成对应的电信号(4～20 mA信号)输出[3]。差压变送器安装示意图如图2所示。

图2 差压变送器安装示意图

蒸发器液位保持在取压口B与取压口C之间。取压口A、取压口B处为液相。取压口C处为气相。取压口A处为液位零点。依据液体压强公式：由差压变送器1测量值计算介质密度ρ；由差压变送器2测量值计算液位L2；由差压变送器3测量值计算液位L1。在取压口C设置充除盐水的冷凝罐，用于隔离高温蒸汽。差压变送器表头布置在低放射性区域。根据液体压强公式，可计算得出废液密度和液位[4]。

依据差压变送器1的测量值，废液密度ρ的计算公式为：

(1)

式中：ρ为蒸发器介质密度；ΔP1为差压变送器1测量值；H1为差压变送器1正负压侧法兰垂直间距；g为重力加速度；ρ1为毛细管硅油密度。

依据差压变送器3的测量值，L1的计算公式为：

(2)

式中：L1为蒸发器液位；ΔP3为差压变送器3的测量值；H2为差压变送器1负压侧法兰与差压变送器2正压侧法兰垂直间距；H3为差压变送器2正负压侧法兰垂直间距；H4为差压变送器3负压侧法兰至冷凝罐垂直间距；ρ2为仪表管除盐水密度。

依据差压变送器2的测量值，L2的计算公式为：

(3)

式中：L2为蒸发器液位；ΔP2为差压变送器2测量值。

2.3 调试运行测量值

在系统调试运行时，以除盐水代替废液。在常压下，20 ℃除盐水密度为0.998 g/cm3，100 ℃除盐水密度为0.958 g/cm3。温度越高，除盐水密度越低[5]。在常温下，除盐水密度值显示为1.0 g/cm3。随着加热器蒸汽流量逐渐增加，蒸发器内除盐水温度上升，除盐水密度计算值下降。在除盐水温度达到100 ℃时，继续增大蒸汽流量，温度不变后密度计算值持续下降。当蒸汽流量达到设计值后保持不变，待系统建立稳定自然循环，达到正常运行工况，介质温度100 ℃，介质密度值显示为0.82 g/cm3左右，小于理论值0.958 g/cm3。由于蒸发器液位是通过密度值计算得出的，密度计算值的偏差导致了液位计算值的偏差。

2.4 测量误差原因分析

经过现场勘查和工艺条件分析，本文得出可能的影响因素，即安装布置和介质流动。

2.4.1 安装布置引起的温度差

取压口B自蒸发器引出后，向下与差压变送器1负压侧毛细管连接，见图2中H2段。在运行中发现，当蒸发器内介质温度为100 ℃时，H2段引压管底部为28 ℃，顶部则为100 ℃左右，上下温度偏差大，导致有较大的密度差。而在密度计算公式中，认为H2段引压管内介质密度与蒸发器内相同，必然引起测量误差[6]。现场实测标高，H1为0.591 m、H2为0.759 m、硅油密度ρ1为0.98 g/cm3。根据密度计算公式，假设H2段引压管内介质温度分别为100 ℃和28 ℃时，H2段引压管温度差引起的密度差值可达0.049 g/cm3。H2段引压管内介质平均温度越低，密度计算值越小。

2.4.2 介质流动引起的压强差

蒸发器在取压口A与取压口B处截面直径不同，存在变径。由于废液蒸发器在蒸发处理时介质循环流动，且蒸发器存在变径，流束在变径处收缩集中，使流速增加，即取压口A处介质流速大于取压口B处介质流速。根据伯努利方程，有：

(4)

式中：P1为取压口A处压强；P2为取压口B处压强；V1为取压口A截面平均流速；V2为取压口B截面平均流速。

从而得到：

(5)

由于V1>V2，P1-P2<ρg(H1+H2)。流速越大，P1-P2越小，则计算得到的密度值越小。在密度及液位计算方法中，液体压强的大小只取决于液体的密度和深度，忽略了介质流速变化产生的压强变化，导致计算结果与理论值存在偏差。在实际运行中，V1、V2无法准确获得。此外，式(4)适用于理想不可压缩流体，在实际应用中还受摩擦阻力等因素的影响[7]，无法准确获得流速变化引起的压强偏差。

2.5 引压管布置问题验证和优化

H2段引压管内介质温度差造成的密度误差可以通过排放介质进行验证。在差压变送器1负压侧法兰连接处排水，用蒸发器内高温介质替换掉H2段引压管内低温介质，使其等温。

记录结果如下：在停蒸汽状态下，蒸发器内介质温度100 ℃，排水前密度值显示为0.93 g/cm3；排水后H2段引压管内介质温度与蒸发器内相同，密度值显示为0.96 g/cm3。排水前后密度测量值相差0.03 g/cm3。经多次验证，H2段引压管温度差对密度测量确有影响。

为消除H2段引压管温度差带来的密度测量影响，可将此段管道去除，使差压变送器法兰与蒸发器取压口水平相接，并对引压管作保温处理。优化引压管后差压变送器安装示意图如图3所示。

图3 优化引压管后差压变送器安装示意图

去除掉H2后再次用除盐水模拟运行，对比上次运行过程，测量密度值变化趋势相同，最小值相比增大。随着蒸汽流量增加，除盐水密度由1.0 g/cm3逐渐降低，在蒸汽流量达到设计值后保持不变。系统建立稳定自然循环后，达到正常运行工况，介质温度为100 ℃，介质密度值显示为0.86 g/cm3左右。

优化引压管后，蒸发运行时的密度测量值较理论值0.958 g/cm3仍有偏差，且蒸汽流量越大，密度测量值越小。而蒸汽流量与自然循环速度成正相关，故判断密度测量受自然循环的速度影响。为了更好地理解自然循环速度对密度测量及液位测量的影响，以下通过模拟软件对蒸发器流场进行模拟仿真。

3 模拟流场

蒸发器二维模型如图4所示。

图4 蒸发器二维模型

为直观了解废液蒸发器运行过程对密度和液位测量的影响，本文使用FLUENT软件进行建模计算。为简化模型，假设蒸发器液位始终保持在循环入口中心位置，即1.8 m液位处，流入与流出保持稳定平衡，省略加热器及蒸发器内气体部分。按实际尺寸建立蒸发器的二维几何模型，蒸发器直径为1.6 m，下出口管道直径为0.345 m。网格划分采用Quad/Tri，网格尺寸为0.01 m，共68 428个网格。

3.1 参数设定

本次模拟只针对蒸发器部分。图4中，入口1为进料口，入口2为循环入口，出口为循环出口，液位保持不变。设定边界条件，入口1为速度入口，入口2为速度入口，出口为自由出口，其他边界为墙。设置FLUENT求解器为压力基，瞬态，重力加速度为9.8 m/s2，计算模型为Realizable k-ε，介质为水，密度0.96 g/cm3，初始化速度、压力为零。本次仿真主要分析变径对流动介质静压的影响。为方便观察，设置操作密度为0.96 g/cm3，即静止状态下介质内部各点压强显示为0，忽略液体自重产生的静压力，计算时需加上液体静压强。

3.2 仿真计算结果

根据工艺设计参数：入口1在充液时最大可达流速约为2.3 m/s，正常蒸发运行时最大流速约为1.8 m/s；入口2最大流速约为2.7 m/s。设置求解器入口1为2 m/s，在入口2分别为0.5 m/s、1 m/s、1.5 m/s、2 m/s、2.5 m/s时，通过模拟计算得到取压口A和取压口B处压强。不同流速下取压口A、取压口B处压强变化趋势如图5所示。

图5 不同流速下取压口A、取压口B压强变化趋势

P1与P2压强差如图6所示。

图6 P1与P2压强差

分别用P1减去P2，计算P1与P2的压差。

由图5和图6可知， 在循环流速不变的情况下，仿真计算在40 s后，压强能保持相对稳定，因此可取40 s后压强的平均值作为密度及液位计算数值。在不同流速下，随着介质循环流速增加，B处压强变化较小，A处压强则大幅降低。模拟仿真中，不涉及差压变送器正负压侧的毛细管硅油及冷凝罐除盐水。将硅油密度及除盐水密度设为0。计算时，将仿真得到的各点压强加上液体静压强。根据式(1)～式(3)，各循环流速的仿真结果如表1所示。

表1 各循环流速的仿真结果

3.3 模拟仿真结论

各流速下流场稳定后，蒸发器侧壁处的压强偏差分布如图7所示。

图7 蒸发器侧壁压强偏差分布

根据表1计算结果可知，随着循环流速的增大，计算得出的介质密度逐渐变小，而液位则逐渐变大，且L1与L2计算得出的液位相同。经与实际运行测量结果相比较，仿真得到的介质密度与调试运行结果趋势相符。以1 800 mm作为液位目标值时，液位高、低报警阈值分别为1 900 mm和1 600 mm。当入口2流速大于2 m/s后，液位偏差已在100 mm以上，在蒸发运行中可能存在实际液位超出高、低阈值的情况。这使得系统安全、稳定运行存在较大风险。

在图7中，蒸发器侧壁压强在下出口最窄处(液位0.7 m)压强最小，循环流速越大，压强偏差越大。测量密度的上、下取压口都必须充满液体。根据压强变化趋势，在模型液位0.7 m上方压强变化最小。由于最低液位原因，取压口可选范围较小，仅有不到0.4 m高度，不满足差压变送器安装条件。如在液位0.7 m下方管道处测量密度，可分别选取液位-1.4 m和-0.5 m处为密度测量差压变送器取压口，压强值分别为P3和P4，据此计算密度值。此段压强变化较为平滑。差压变速器2和差压变送器3的取压口不变，压强值见表1中P1和P2，据此计算液位值。优化取压口位置后，密度与液位计算结果如表2所示。

表2 优化取压口位置后密度与液位计算结果

取压口位置优化后密度偏差变小，L2偏差变小，但L1偏差变大。L2的偏差范围很小，可以满足系统运行需求;但L1偏差范围过大，无法满足系统运行需求。液位偏差是由废液蒸发器的工艺条件和差压法测量原理决定的，可以减小但难以避免。由于优化取压口位置后L1偏差过大，故考虑在此处取消差压变送器，使用其他原理的液位计代替。

4 其他液位测量方法

除差压式液位计外，核电厂中常用的液位计还有浮球液位计、静压式液位计、电容式液位计、雷达液位计、磁翻板液位计和浮筒液位计等[8]。废液蒸发器可考虑选用其他测量原理的液位计。蒸发器内二次蒸汽设计温度160 ℃，设计压力0.5 MPa。蒸发器顶部距底最大距离为4 m。废液具有高放射性，其中的化学物质包括各种盐类及悬浮固体。根据废液蒸发器介质特性与安装条件，可选用分体式导波雷达液位计进行液位测量。

导波雷达液位计基于时域反射原理，高频率的微波脉冲沿导波杆传播。当遇到被测介质表面时，由于介电常数发生突变，微波脉冲被反射形成回波并沿相同路径返回，仪表电子部件通过分析微波脉冲运行时间算得出液位高度。高频率的导波雷达液位计对蒸汽不敏感，不受被测介质的密度、介电常数、温度、压强等工艺条件变化影响，在导波杆上粘附介质也不会影响测量结果，安装维护简单，测量精度高[9-11]。分体式导波雷达可将仪表电子部件安装在远离高放射性区域，以提高仪表使用寿命。导波雷达液位计安装示意图如图8所示。

图8 导波雷达液位计安装示意图

分体式导波雷达液位计安装在废液蒸发器顶部。由于其测量原理不同于差压变送器，避免了介质温度差异和流速变化导致的测量误差。如同时采用导波雷达液位计和差压式液位计，可以避免液位计共因失效的发生，增强液位测量的可靠性。

5 结论

自然循环废液蒸发器由于介质流动及上、下取压口存在变径的影响，差压变送器会产生测量偏差，流速越大，偏差越大。对密度及液位计的安装及选型可采用以下优化措施。

①重新选择取压口位置，测量密度的差压变送器上、下取压口优先布置于同管径位置，以及液位差压变送器下取压口优先布置于管径较大位置，从而减少由伯努利效应产生的压强偏差所带来的影响。

②增加其他液位测量方式。导波雷达液位计不受介质压强等工艺条件变化的影响，应用2种测量原理的液位计可以增加液位测量值可靠性，确保系统稳定运行。

在工程实践中，某些测点存在的缺陷和不足很难被发现和解决。对此，只有不断地吸取经验反馈，应用更先进、成熟的测量技术，持续优化和改进，才能提升核电厂安全性和自动化水平。