介质粗糙面与埋藏导体目标的电磁散射特性研究

张亚，何红杰

（郑州轻工业大学，河南郑州，450000）

0 引言

粗糙面与目标的复合电磁散射特性研究应用广泛，在雷达监控、遥感和目标识别等领域具有重要的实际应用价值。近几十年来，针对粗糙面与目标的复合电磁散射问题，各国学者提出了多种研究方法，根据其求解机制不同，这些方法大致可以分为三类：高频近似方法[1-3]、低频数值方法[4-7]和高低频混合算法[8-11]。随着计算机技术的飞速发展，数值算法由于其较高的计算精度受到越来越多学者的青睐。目前，求解三维复合电磁散射问题的常用数值方法主要包括矩量法(Method of Moment, MoM)[5-7,12]、时域有限差分方法(Finite Difference Time Domain, FDTD)[13,14]和有限元-边界元方法(Finite Element Method-Boundary Integral Method, FEM-BIM)[4,15]。例如，文献[5]将电场积分方程与局部粗糙表面的并矢格林函数结合研究了二维介质粗糙面下方埋藏介质目标的电磁散射特性，但随机粗糙表面的并矢格林函数一般是难以预知的，因此该方法不适用于处理随机粗糙表面的电磁散射问题；Wei等人采用基于单积分方程的MoM研究了介质粗糙面上/下方目标的电磁散射特性[12]，由于单积分方程的未知量仅为传统MoM未知量的一半，因此，基于单积分方程的MoM在求解时间和内存消耗方面都具有明显的优势；Lai等人将区域分解技术与FDTD方法结合，计算了大尺度粗糙面的电磁散射[13]；Tian等人采用改进的FDTD方法分析了强脉冲源入射下粗糙地面上方电介质涂层导线的瞬态耦合特性[16]。

FEM-BIM方法结合了FEM和BIM两种方法的优势，具备处理复杂结构非均匀媒质电磁散射问题的能力，该方法在目标与粗糙面复合电磁散射特性研究方面的应用也已有报道。Xu等人将采用FEM/MoM求解了一维/二维粗糙面上方二维/三维目标的电磁散射[4,17]，但Xu的工作均采用传统的LU分解算法求解复合模型的FEM/MoM矩阵方程组，虽然具有较高的计算精度，但内存消耗较大且求解效率不高；针对FEM-BIM矩阵方程组的特点，本文作者将FEMBIM与快速多极子技术(Fast Multipole Method, FMM)[18,19]结合计算了水平极化和垂直极化波入射下一维分层介质粗糙面上方二维涂覆目标的双站散射系数(Bistatic Scattering Coefficient, BSC)[20]，显著提高了仿真效率；Sun等人将FEM/MoM方法与多层快速多极子技术结合计算了二维介质粗糙面上方三维介质目标的电磁散射[15]，极大地提高了计算效率，减少了内存资源消耗。但上述工作均针对粗糙面上方目标的散射问题，将FEM-BIM-FMM应用于二维介质粗糙面下方导体目标电磁散射特性的研究还未见报道。

本文将三维矢量FEM-BIM与FMM结合研究了二维介质粗糙面下方导体目标的复合电磁散射特性，推导了复合模型电磁散射的FEM-BIM-FMM公式。在仿真中，采用FEMBIM处理导体目标的散射场，为了保证收敛速度，采用PMCHW积分方程组处理介质粗糙面的散射场，导体目标与粗糙面之间的耦合场通过复合模型表面的积分方程进行考虑；针对FEM-BIM矩阵方程组的特点，采用混合求解器求解复合模型的矩阵方程组，并采用FMM加速迭代求解过程；通过与MoM和传统FEM-BIM的对比，验证了本文算法的精确性和高效性；最后，结合Monte-Carlo方法，数值模拟了二维粗糙地面下方炸弹型导体目标的电磁散射，分析了土壤湿度、埋地深度和地面粗糙度等参数对复合模型电磁散射特性的影响。

1 理论模型及公式推导

图1为二维介质粗糙面下方埋藏导体目标的电磁散射模型，其中粗糙面Ss被截断为正方形区域，其长度为L，为粗糙面的外法向单位矢量，粗糙面上半空间 ΩU的相对介电常数和磁导率分别为εU和µU，下半空间 ΩD的相对介电常数和磁导率分别为εD和µD；锥形入射波Einc以入射角θinc和φinc照射到复合模型表面，Js和Ms为粗糙面上的感应电磁流。

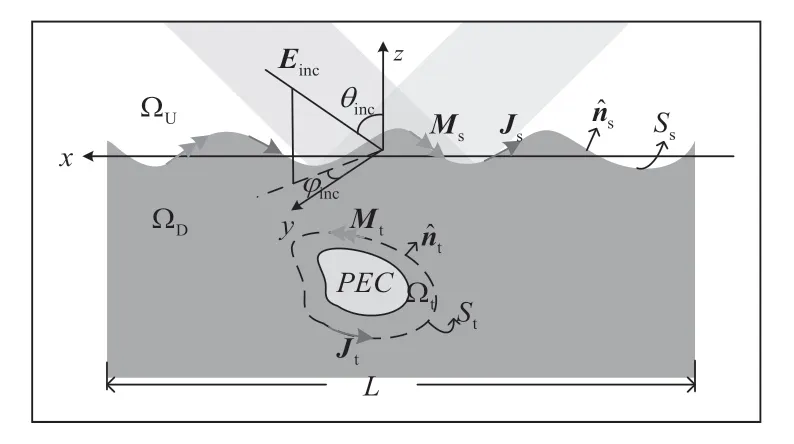
图1 二维介质粗糙面下方埋藏导体目标的电磁散射模型

采用FEM方法处理导体目标的内部场。取虚构边界 tS将导体目标包围，内部空间为 tΩ，tˆn为 tS的外法向单位矢量；tJ和 tM分别为目标表面的感应电磁流。根据有限元方法的基本思想， Ωt内部的电场E(r)可以通过求解下面的等效变分问题获得：

其中：

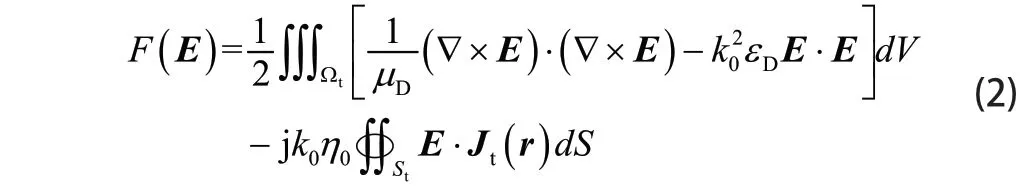
式中k0和η0分别表示真空中的波数和波阻抗。采用四面体单元和Whitney矢量基函数N(r)[21]将 Ωt内的电场E(r)离散，表达式为：

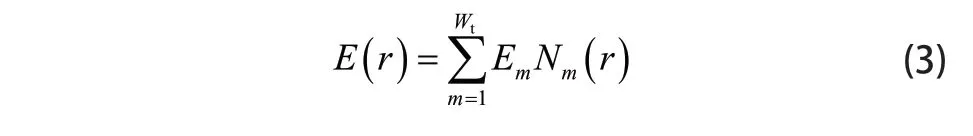
其中 tW表示四面体棱边的个数，mE为电场展开系数。同时采用RWG基函数f(r)[22]将St上的感应电磁流离散，表达式为：

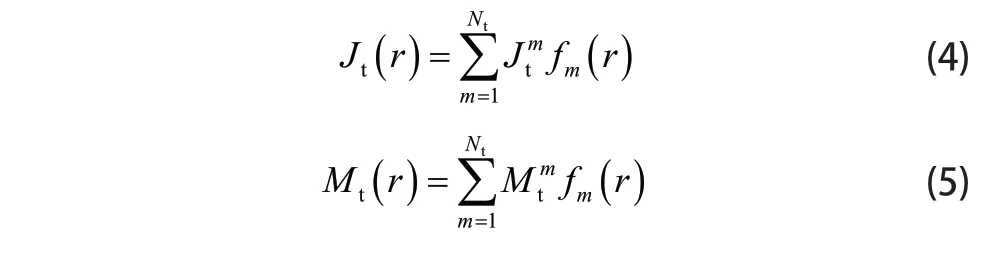
式中 tN为虚构边界上三角形棱边的个数。将(3)式和(4)式代入到(2)式可以得到下面的有限元矩阵方程组：

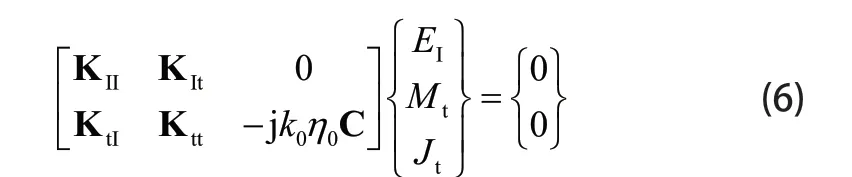
其中：

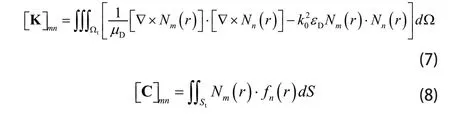
介质粗糙面及目标的耦合场采用BIM方法考虑。虚构面 tS上的场满足下面的电场积分方程：

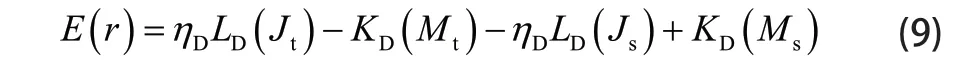
其中ηD为空间 ΩD的波阻抗，算子L(X)和K(X) 的表达式为：

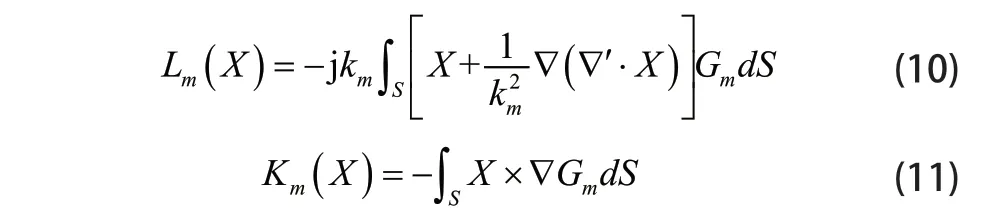
其中G表示格林函数。粗糙面上的场可以用PMCHW积分方程描述，表达式为：

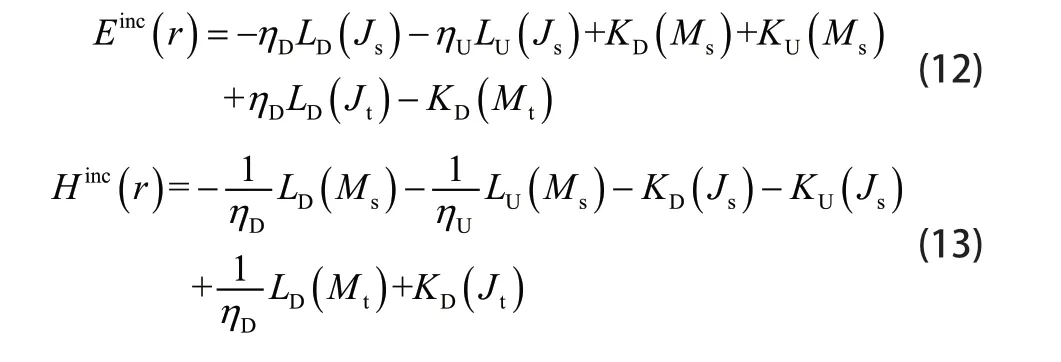
其中 Uη为空间 UΩ 的波阻抗。将粗糙面用三角形面元离散后，粗糙面上的未知量可以用RWG基函数展开为：

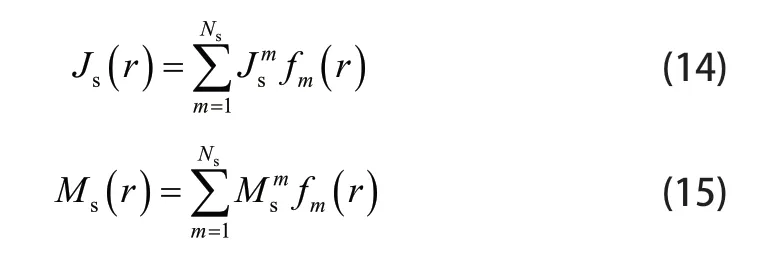
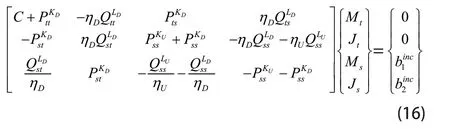
式中：

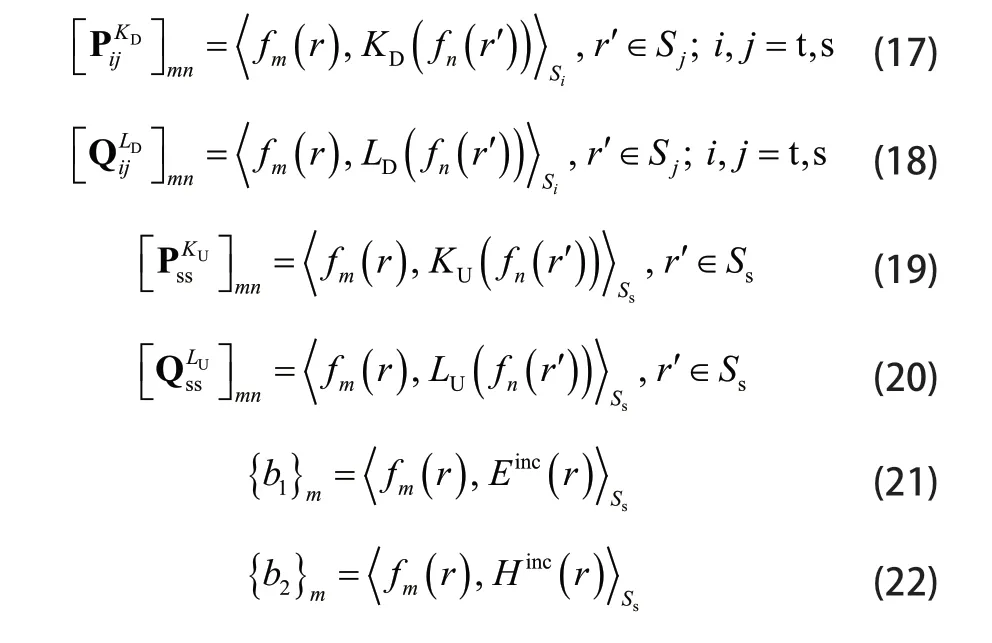
联立(6)式和(16)式即得到了复合模型的FEM-BIM矩阵方程组，求解该方程组即可得到模型表面的电磁流信息。为了提交求解效率，本文采用LU分解法和广义最小残差法（Generalized minimal residual method, GMRES）混合迭代求解FEM-BIM矩阵方程组，首先假定{Jt}= 0、 {Ms}=0和{Js} = 0，结合{Jt}采用LU分解法求解(6)式，得到{Mt}；然后结合{Jt}、{Mt}、{Js}和{Ms}用GMERS求解(16)式，得到新的{Jt}、 {Mt}、{Js}和{Ms}；直到迭代误差小于10-3。

获得模型表面的电磁流信息后，可以采用下式计算复合模型的BSC：

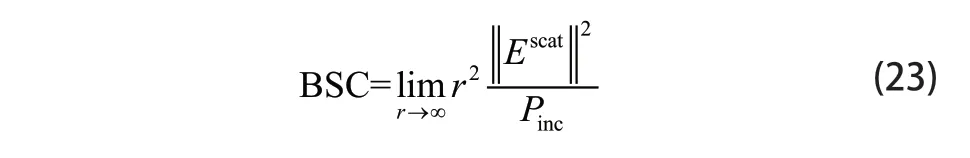
其中Escat(r)为复合模型在上半空间中的散射场，其计算表达式为：为入射波功率，式中g =L4表示锥形波因子。

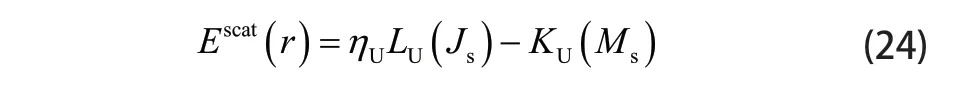
为了提高仿真效率，本文采用快速多极子技术加速GMRES迭代求解过程。按照快速多极子的思想将复合模型表面的未知量分组后，面元间的强相互作用仍然采用(17)~ (20)式计算，而弱相互作用则由下面各式计算。

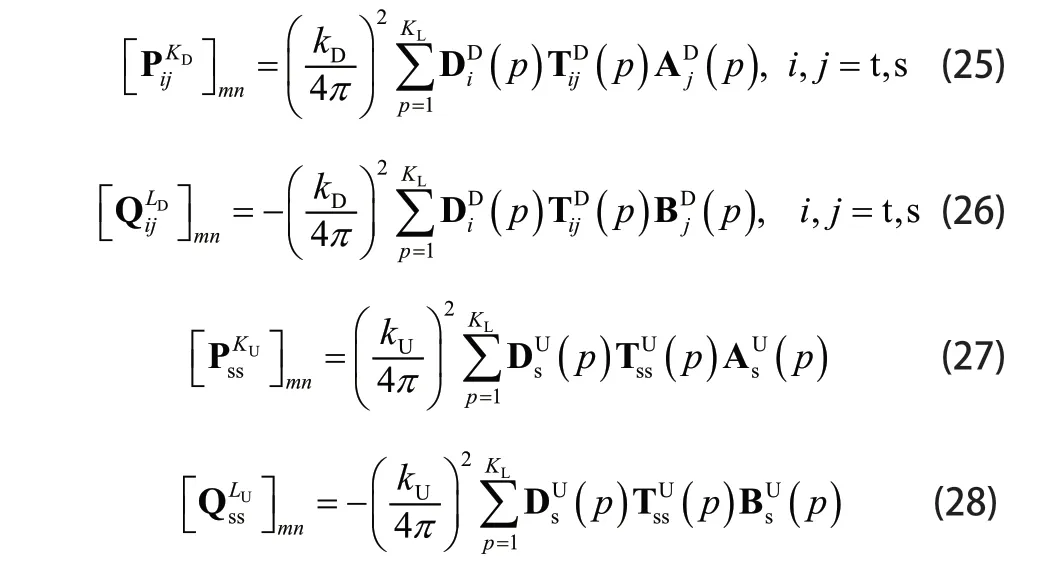
其中Uk和Dk分别为空间 UΩ 和 DΩ 中的波数，矩阵A、B、T和D的表达式如下：

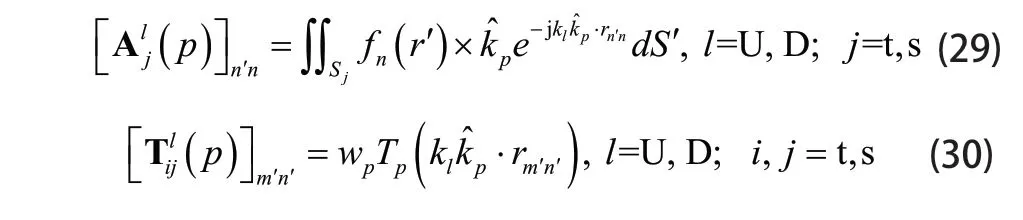
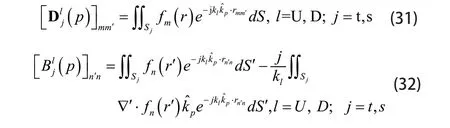
其中当l=U时，, sij= 。

2 数值算例

为了验证算法的正确性，分别采用FEM-BIM、MoM和FEM-BIM-FMM计算二维高斯介质粗糙面下方导体立方体的双站散射系数，仿真实现的硬件平台为：AMD Ryzen 9 5950X CPU， 内存：32 GB。模型参数设置如下：粗糙面尺寸8m × 8m，均方根高度δ= 0.05 m ，相关长度lc= 0.15 m ，εD= 2.0 - j0.2，µD= 1.0，立方体的边长为0.6 m，埋藏深度3.5 m，入射波为横电波（TE波），频率为0.3 GHz。图2给出了三种方法的对比结果，从图中可以看出，两种入射角下，三种方法的计算结果均吻合良好，验证了本文算法的正确性。表1给出了FEM-BIM和FEM-BIM-FMM的求解时间及内存需求对比，从表中可以看出，FEM-BIM-FMM的求解时间和内存需求分别为传统FEM-BIM的14.6%和9.2%，计算资源消耗明显减少，说明了本文算法的高效性。

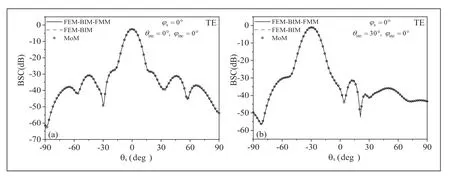
图2 二维介质粗糙面下方金属立方体的BSC:(a) inc=0θ °；(b) inc=30θ °

表1 不同方法计算介质粗糙面下方金属立方体BSC时的求解时间及内存需求对比

下面采用FEM-BIM-FMM方法分析地面下方炸弹型金属未爆物的电磁散射特性。炸弹型金属未爆物的几何尺寸如图3所示，埋地深度1.0 m；地面几何尺寸为10m10m× ，土壤是由空气、水和固态土壤等组成的介电混合体，其相对介电常数受土壤湿度、土壤温度、土壤含沙量和土壤黏土含量等因素的影响，本文采用Wang等人建立的四成分模型来描述土壤的介电常数[23]。在本文后面的算例中取土壤温度为T= 20°C ，土壤湿度mv= 0.1gcm3，土壤含沙量S= 17.2%，黏土含量C= 19.0%。入射波的参数与上例相同。

图3 金属炸弹型目标几何尺寸示意图

图4 分析了土壤湿度 vm变化对复合模型电磁散射特性的影响。从图中可以明显看出，两种入射角下，对于确定的土壤类型（土壤含沙量和黏土含量保持不变），随着土壤湿度 vm的增大，BSC在整体上呈现出明显增大的趋势。这主要是因为，土壤湿度变化对土壤介电常数有较大的影响，且随着湿度的增大，土壤介电常数实部增加明显，导致反射增强，BSC增大。

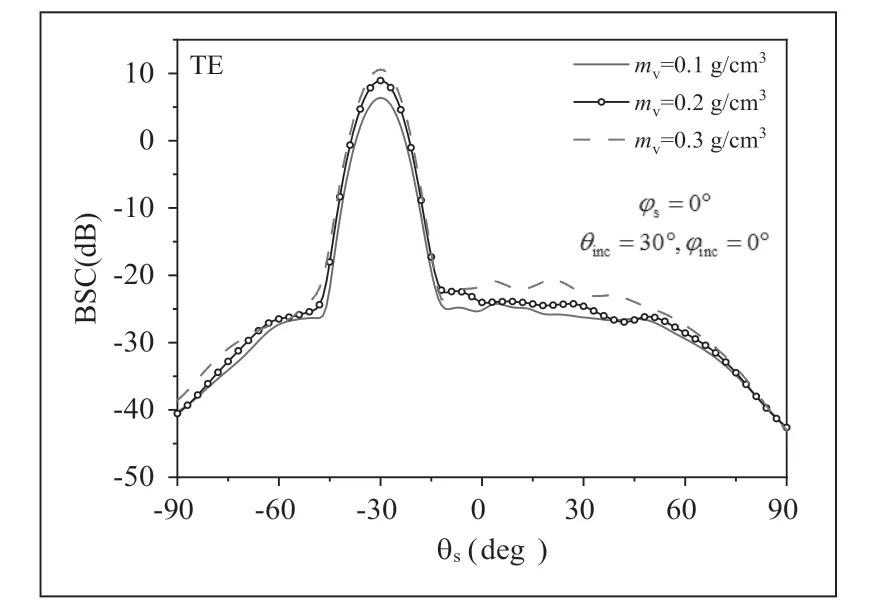
图4 不同土壤湿度mv时地面下方埋藏炸弹型目标的BSC

图5 分析了炸弹型目标的埋地深度变化对复合模型电磁散射特性的影响。如图所示，两种入射小下，埋地深度变化对镜向散射角附近的BSC几乎没有影响，但对其它散射角方向的BSC影响较大，且随着埋地深度的增大BSC呈现出减小的趋势。这主要是由于镜向散射角附近的散射场主要来源于地面反射，而目标的存在主要影响非镜向方向的散射场，因此埋地深度变化主要影响非镜向角方向的BSC。

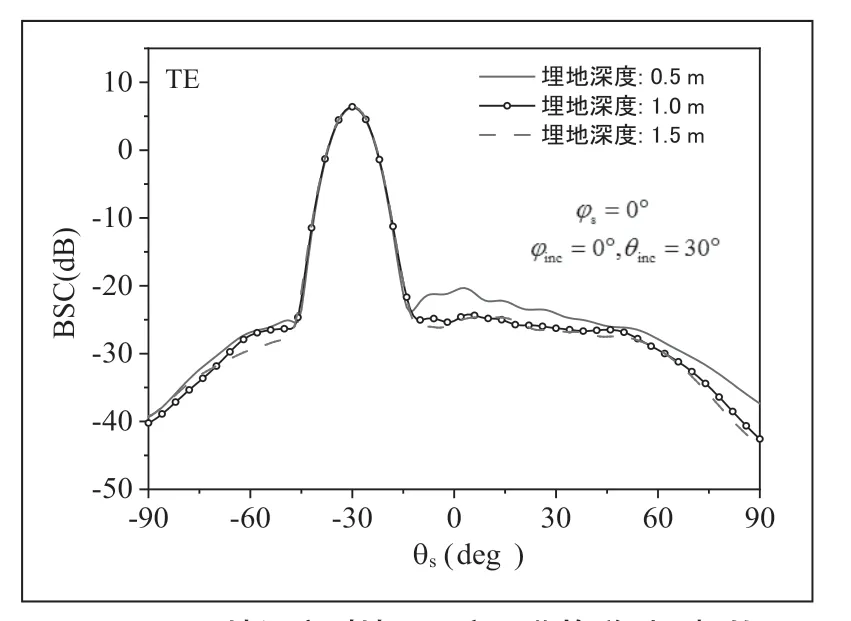
图5 不同埋地深度时地面下方埋藏炸弹型目标的BSC

图6 分析了地面粗糙度变化对复合模型BSC的影响，其中相关长度lc= 1.0m ，从图中可以看出，随着均方根高度δ的增大，镜向方向的BSC明显减小而其它散射角方向的BSC明显增大，这主要是由于当δ增大时，地面粗糙度增加，镜向反射减弱而漫反射增加，导致非镜向角方向的BSC增大。

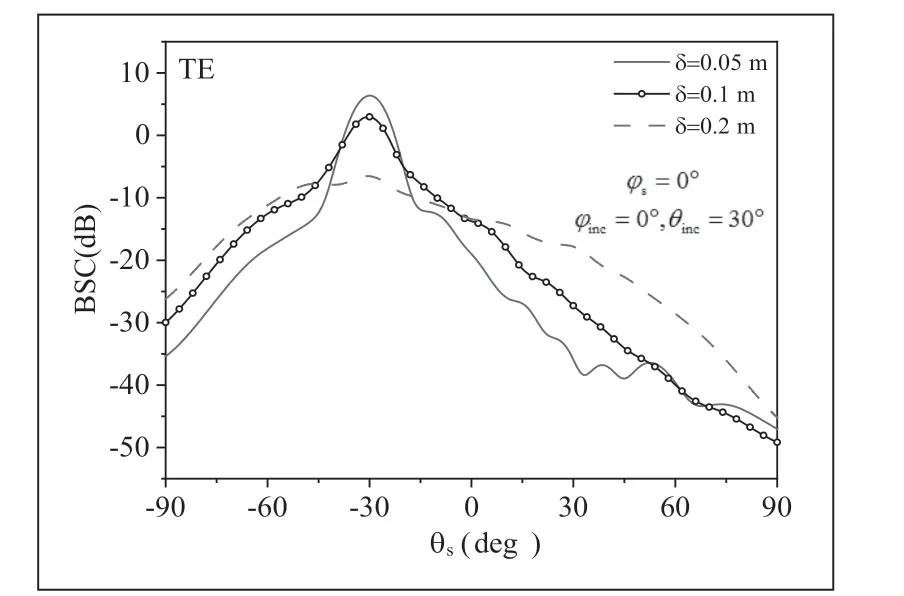
图6 不同均方根高度时地面下方埋藏炸弹型目标的BSC

3 结论

本文将FEM-BIM与FMM结合，提出了一种用于研究二维介质粗糙面下方金属目标电磁散射特性的高效数值算法，推导了FEM-BIM-FMM的理论公式，采用PMCHW积分方程处理粗糙面的散射场，埋地目标的散射场采用FEMBIM处理，目标和粗糙面之间的耦合场通过模型表面的积分方程进行考虑。根据模型矩阵方程组的特点，采用用FMM加速的混合求解器求解FEM-BIM矩阵方程组。与传统FEM-BIM方法相比，在保证计算精度的前提下，FEM-BIMFMM可以极大地提高仿真效率，降低计算机内存需求。最后，结合Monte-Carlo方法，数值分析了二维介质高斯粗糙面下方炸弹型金属目标的电磁散射特性，研究了土壤湿度、炸弹埋地深度和地面粗糙度对复合模型BSC的影响，并给出了一些有意义的结论。