基于HOG特征的加权稀疏表示人脸识别算法
高纪东,王正群,夏 进
(扬州大学 信息工程学院,江苏 扬州 225127)
0 引 言
随着科学技术的不断发展,图像识别技术在计算机视觉和模式识别以及人工智能等领域受到了广泛的关注,在生物识别、人脸检测以及身份验证等方面拥有广阔的应用前景。然而,采集的图像会受到多种不稳定因素的影响,导致系统识别性能受到干扰[1]。近年来,随着压缩感知理论[2]的发展,使得稀疏表示受到了广泛的关注。Wright等人[3]首先提出基于稀疏表示分类(sparse representation classification,SRC)的识别算法,该算法利用测试样本和训练样本之间的重构残差进行样本的识别分类,在一定程度上,该算法提高了人脸识别的性能。随后,Wagner等人[4]提出一种新的稀疏表示算法。该算法在不同光照下采集训练样本,提高了人脸识别效果,但算法复杂性高。虽然稀疏表示理论提供了一种新的特征提取模式,但传统的稀疏表示算法容易忽视样本间的距离相似性。对此,Fan等人[5]提出一种加权稀疏表示(weighted sparse representation classification,WSRC)的识别算法,将训练样本和测试样本的距离作为训练样本的权重,利用加权训练样本对测试样本进行表示并分类。该方法在解的稀疏性上优于上述稀疏表示算法,但算法耗时且不符合实时性要求。Wang等人[6]提出基于自步学习的加权稀疏表示算法,一方面剔除与测试样本相差较大的训练样本,另一方面考虑了样本的局部信息,提高了稳定性,但在模型学习过程中较依赖数据标签。
Dalal等人[7]提出一种基于HOG特征的行人检测算法,指出HOG算子可以有效提取行人图像的局部梯度和方向信息,描述行人图像的局部特征和外部轮廓,提高行人检测识别效率。而Zhao等人[8]将稀疏表示和HOG特征提取相融合,提出基于稀疏表示和HOG特征的掌纹识别方法,该方法降低了算法的复杂度,一定程度上提高了识别性能。近年来,HOG算子被广泛应用于特征提取方面并取得了很好的效果。但在对HOG特征的相关研究中,往往是简单的将HOG特征应用到人脸的全局特征和局部特征中,并没有考虑到光照等不同噪声因素以及对人脸识别效果造成的影响。
为了提高系统的识别效果,该文提出一种基于随机投影[9]和HOG特征提取的加权稀疏表示算法(weighted sparse representation algorithm based on random projection and hog feature extraction,RPH-WSRC)。该算法首先利用HOG算子对图像进行特征提取,清晰地描述出图像的局部信息;其次,引入随机投影矩阵对得到的样本进行多次投影,充分挖掘数据样本潜在的信息,保持样本的结构信息[10];最后,RPH-WSRC算法将训练样本和测试样本之间的相似性作为权重,设计加权稀疏表示方法。在多次随机投影的过程中,会产生多个样本残差,将同类别的样本残差融合得到稳定性更高的残差和,从而实现更加稳定和鲁棒的人脸识别效果。
1 方向梯度直方图
方向梯度直方图(histogram of oriented gradient,HOG)根据图像轮廓处的梯度方向的直方图提取图像的特征,通过提取图像中的关键信息进而简化图像。因此HOG特征是描述图像特征局部信息的一种非常有效的方法[11]。Dalal等人首次将HOG算子用于行人图像中,提出基于HOG特征的行人检测算法,并将其与分类器配合,用于行人检测。近年来,很多学者将HOG算子用于人脸检测识别[12],并且提高了人脸图像的识别性能。
方向梯度直方图是一种非常有效的图像特征描述子,其主要目的就是将图像进行灰度化、归一化以及梯度计算,从而统计图像的梯度信息[13]。由于方向梯度对部分噪声相当敏感,而高斯平滑滤波器可以平滑带有噪声的图像,并且可以去除图像中的噪声[14],故在该算法中引入高斯函数,利用高斯函数对图像进行卷积,获得水平和垂直两个方向的梯度。以下为HOG特征提取的步骤:
(1)将原始图像进行灰度化、归一化处理。
(2)分别计算处理后的图像中的每个像素梯度方向和幅值大小。
(1)
其中,Ix,Iy和H(x,y)分别为像素点的水平梯度、垂直梯度和像素值。
(2)
其中,M(x,y)为梯度的幅值大小,θ(x,y)为像素的梯度方向。加入高斯函数后获得新的水平和垂直梯度为:
(3)
其中,G为高斯函数,I为图像的灰度图。Gx,Gy为高斯函数在水平和垂直方向上的一阶导数,Fx(x,y)和Fy(x,y)为经过高斯函数平滑后的图像水平和垂直方向的梯度。
(4)
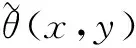
(3)将图像划分为同等大小的细胞单元(cell)。
(4)将360度分为9个区域,即图像的直方图分为9个bin,将每一个cell的幅值按梯度方向对应的区域进行累加,然后统计每一个cell的bin,最后统计出该cell的直方图,形成每一个cell的HOG特征。
(5)将几个cell合成一个block,把一个block内的所有cell的HOG特征串联起来归一化便得到该block的HOG特征。
(6)将所有block的HOG特征串接起来作为整幅图像的HOG特征。
2 基于HOG特征的加权稀疏表示人脸识别算法
传统的稀疏表示是利用训练样本和测试样本间的重构残差来判断测试样本的类别,虽然在一定程度上识别效果有所提升,但是在不同影响因素下,同一类人脸图像差异很大,使得仅靠单一的残差判断测试样本的所属类别的方法变得不可靠。因此,该文在加权稀疏表示的基础上引入随机投影矩阵,获得多个残差,利用残差和识别分类。
2.1 随机投影
随机投影(random projection,RP)是一种有效的降维方法,在降低维数的同时,能够保持数据的结构特性,并且能够在一定程度上降低样本的噪音,而且不依赖数据样本,投影矩阵能够随机产生。因此将随机投影引入稀疏表示中,更能够提高其识别效率。
随机投影用来降维和数据投影的理论依据来源于 Johnson-Lindenstrauss定理[15]。该定理指出:对任意常数0<ε<1和任意正整数n,设k是一个正整数,有:
k≥4(ε2/2-ε3/3)-1lnn
(5)
那么对于任意Rd空间中的n个点构成的集合V,始终存在一个映射f:Rd→Rk使得对所有的u,v∈V,有:
(6)
其中,ε为随机投影误差,是一个正常数,即 0<ε<1。该定理表示任意n维样本可以通过随机矩阵R∈Rd×q映射至d维空间。
2.2 算法(RPH-WSRC)实现
将测试样本和训练样本进行多次随机投影,进而得出投影后的训练样本和测试样本,利用高斯核函数计算测试样本和训练样本间的相似度作为稀疏系数的权重,进而进行稀疏表示识别分类,在很大程度上降低了系统的计算量。RPH-WSRC算法的具体步骤如下:

(2)引入随机投影矩阵Q。利用随机投影矩阵将训练样本和测试样本迭代T次,T≥2。假设第t次样本的投影的随机矩阵为Qt∈Rd×q,其中d (7) (3)计算权重。在进行第t次迭代时利用高斯核函数计算测试样本和每一个训练样本的相似性,即权重为: (8) yt=Xta (9) 其中,a=(0,0,…,ai1,ai2,…,ain,…,0,0),表示与第i类样本同类的稀疏系数不为0,不同类样本的系数为0,此时根据稀疏系数a中的分布就可以判别出测试样本属于训练样本中的哪一类。 (5)引入权重,构造新的稀疏系数,即: (10) (6)求解L0最小化问题: (11) (12) (13) 此时第t次随机投影及稀疏表示结束。 (8)计算迭代t次以内的同类样本的重构残差和。当样本迭代T次,产生T个随机投影矩阵时,会进行多次稀疏表示,并且每个样本经过迭代后得到该样本对应的重构误差,并且经过t次迭代后的误差之和为: (14) (15) 其中,identity(y)为测试样本y所属的类别。当迭代第t-1次和第t次的识别结果相同或者t=T时,迭代结束。 算法:基于随机投影和HOG特征提取的加权稀疏表示算法。 (1)提取特征图像。提取每一个训练样本和测试样本的HOG特征图像。经过处理后的训练样本为X={x1,x2,…,xc}∈Rq×n,测试样本为y。 (2)将训练样本中的每一列进行归一化。 (4)计算权重。利用等式(8)计算第t次迭代时测试样本和每一个训练样本间的相似性,即权重。 (5)利用式(10)计算加权后的稀疏系数。 (6)利用式(13)计算第i次迭代时测试样本和每一个训练样本的残差。 (7)通过式(14)计算t次迭代过程的重构残差之和。 (8)当迭代第t-1次和迭代t次的结果相同,即identity(y)t-1=identity(y)t时,停止迭代或当t=T时,停止迭代。此时通过式(15)来判断测试样本的类别。 该实验在两个常用的数据集上进行,即ORL以及GT人脸数据库。为验证该算法的有效性,将RPH-WSRC与PCA-SRC[16]、WSRC以及HOG-SRC[8]算法进行对比。在人脸数据集中分别加入均值为0、方差为0.1的高斯噪声以及密度为0.1的椒盐噪声,进行仿真实验,检验该算法的可行性。 ORL人脸数据库:该数据集共有400张图像,其中包含40组人脸图像,每组图像由10张图像组成,在不同角度不同环境不同面部表情方面各不相同,并且每张图像尺寸大小为112×92。图1展示了ORL数据集部分人脸图像和添加高斯噪声后的人脸图像,以及添加椒盐噪声后的人脸图像。在每组图像中选取T(T=4)幅人脸图像作为训练样本,剩下的作为测试样本。对每组实验分别重复进行10次,取10次实验的平均识别率,比较在不同维度下几种算法的识别率,结果如表1所示。 图1 ORL数据集下添加噪声的人脸图像 表1 ORL库上各算法在不同噪声下的平均识别率 % 表1展示了PCA-SRC、WSRC、HOG-SRC以及RPH-WSRC的实验结果。可以看出,文中方法RPH-WSRC在是否存在噪声的情况下均有很好的识别效果。当训练样本相同时,在无噪声的情况下,RPH-WSRC分别高了16.10%、13.26%和11.16%。当样本加入不同类型的噪声后,各算法的识别率均受到不同程度的影响,但RPH-WSRC算法的平均识别率仍能达到最高,说明RPH-WSRC算法具有较强的抗干扰能力。另外在本次实验中,文中算法与WSRC算法的识别率总是高于PCA-SRC的,说明对PCA-SRC给予合适的权值确实能提高人脸识别率;而WSRC算法识别率略低于HOG-SRC方法,说明提取局部特征在一定程度上更有利于识别分类。从表1的结果进一步表明,RPH-WSRC算法在局部特征的提取以及识别方面都有很大的提高。 图2为在ORL数据集下各算法的识别率曲线。从图中可以看出,在总体上,几种算法的识别率随着特征维数的增加呈上升趋势,最后逐渐走上稳定趋势,虽有一些波动,说明并不是所有的特征都有利于分类识别。在对人脸图像添加噪声后,图像受到污染遮挡,但RPH-WSRC算法识别率高于其他算法,说明文中算法对噪声具有一定程度的鲁棒性。 图2 ORL数据集下的各算法实验识别率曲线 GT人脸数据库[17]:Georgia Tech database(GT)数据库包含50组人脸图像,每组包含不同表情不同姿势的15组图像,共750幅图像,并且将图像尺寸大小调整为120×80。图3展示了GT数据集部分人脸图像和添加高斯噪声后的人脸图像,以及添加椒盐噪声后的人脸图像。对每组实验分别进行10次,取10次实验的平均识别率,比较在不同维度下几种算法的识别率,结果如表2所示。 图3 GT数据集下添加噪声的人脸图像 表2 GT库上各算法在不同噪声下的平均识别率 % 表2展示了各算法在GT人脸数据库上的平均识别率,由于GT人脸数据库中的同类样本间在笑的程度、是否扭头以及扭头的程度和光照强度上有很大的差异,导致各算法在GT人脸数据库上的平均识别率要远远小于在ORL数据库上的识别率。该实验是选取T(T=6)幅图像作为训练样本,其余的为测试样本。在表2中可以看出,文中算法要优于其他几种算法;虽然稀疏表示对噪声具有一定的鲁棒性,但当图像遭受的损坏程度较大时,则识别效果会下降很多,而HOG-SRC算法对光照具有很好的鲁棒性,其识别效果会优于单独的稀疏表示。而文中算法的识别率比其他几种算法高,说明了RPH-WSRC算法对一些被损坏程度较大的图像有着更好的识别效果。图4为各算法在不同噪声下的识别率曲线,可以看出RPH-WSRC的识别率保持最高,其抗噪声能力均优于其他几种算法。 图4 GT数据集下各算法的识别率曲线 为了提高人脸图像对光照等外界因素的鲁棒性,该文提出一种基于随机投影和HOG特征提取的加权稀疏表示算法RPH-WSRC。该算法首先对图像进行预处理并利用HOG算子对原始图像进行特征提取,之后,利用随机矩阵对得到的样本图像进行多次投影,用来挖掘数据信息,保持样本结构信息;最后考虑样本之间的相似性,将这种相似性作为稀疏系数权重,利用同类别样本的残差和最小值判断测试样本类别。在ORL人脸数据库和GT人脸数据库上的实验证明,该方法不仅有较好的局部特征提取能力,而且在噪声的干扰下也有很好的鲁棒性。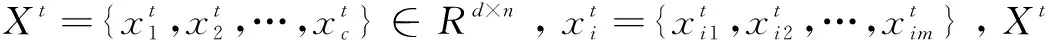


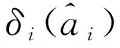
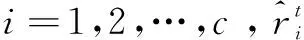

3 实 验
3.1 ORL人脸数据库实验
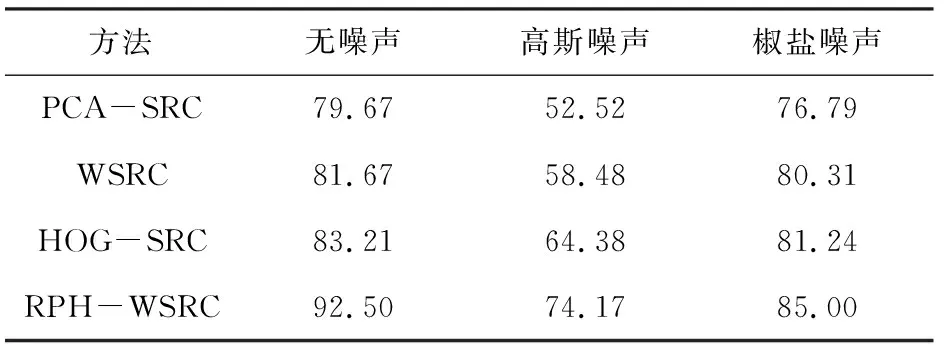
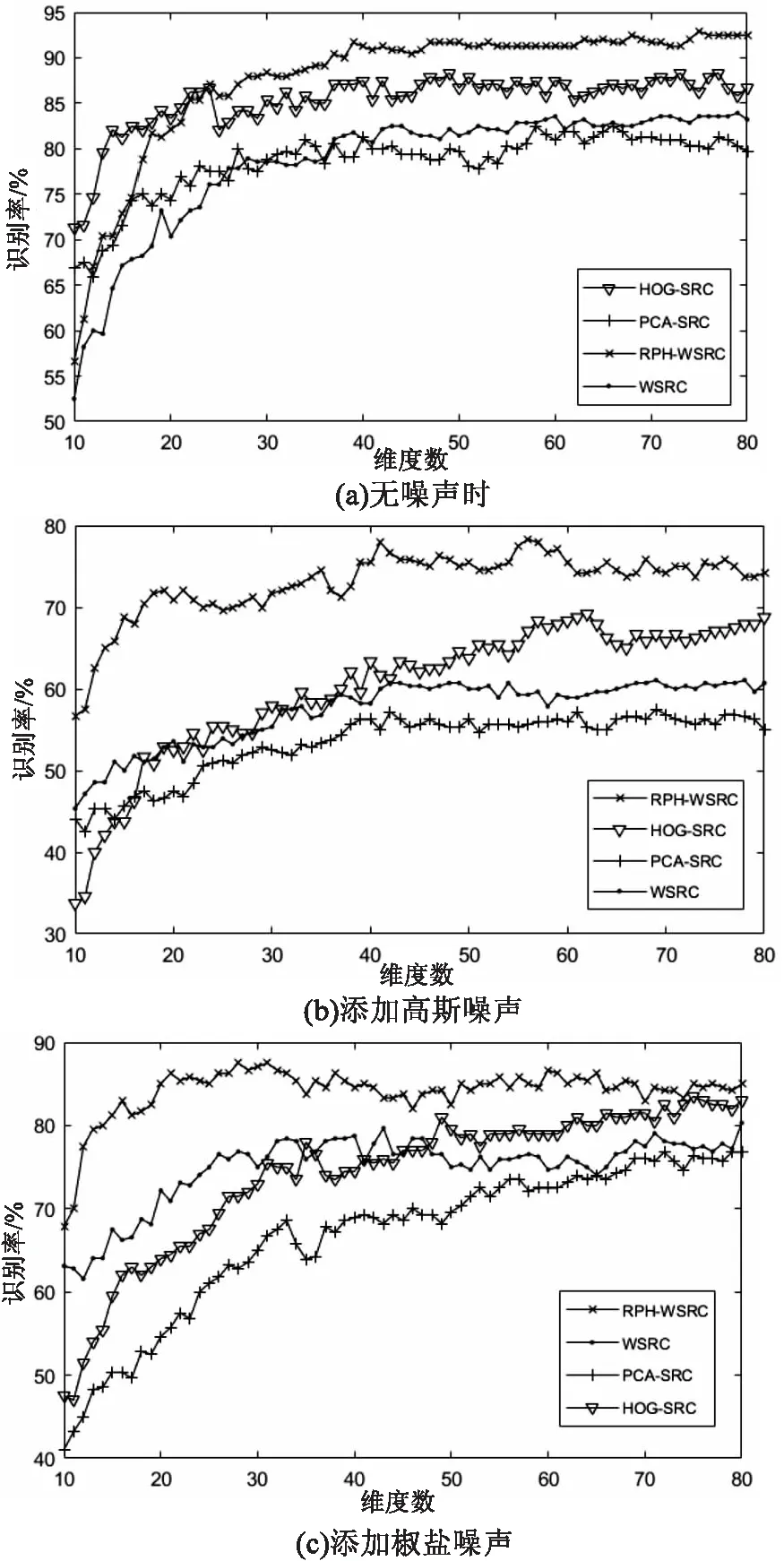
3.2 GT人脸数据库实验


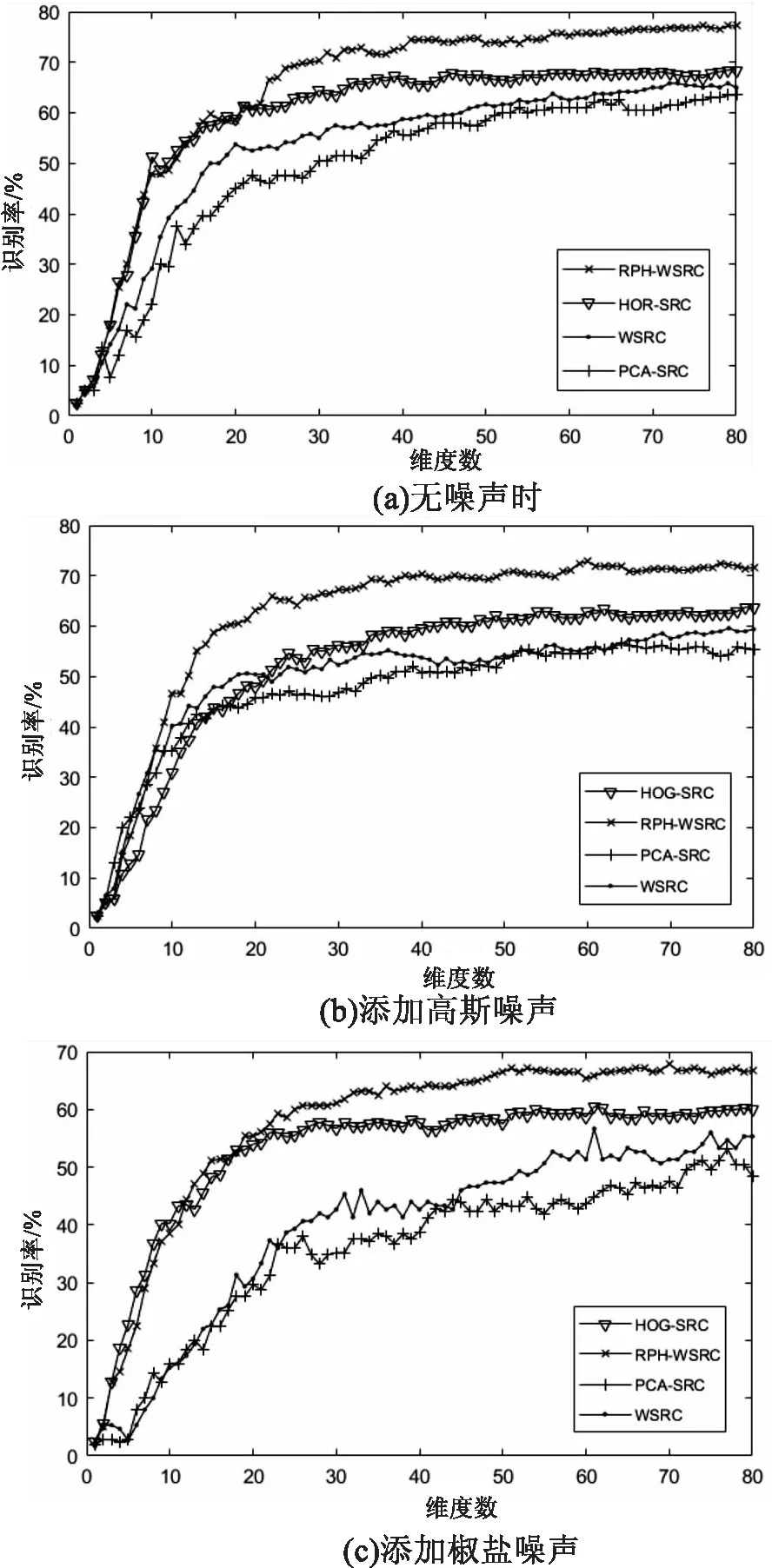
4 结束语

