一种基于SuperGlue 的兵力部署估计方法*
高顺凯
(武汉市江夏区藏龙大道709号 武汉 430205)
1 引言
未来战场需要较高的自动化指控能力[1],从而提高部队的反应速度,战术辅助决策正是实现此能力的关键技术。在作战前进行辅助决策时,会根据作战对象和作战地点的具体情况,对作战态势进行感知[2];在作战过程中,辅助决策可以帮助指挥员快速、准确地进行决策,为我方作战提高优势。
对敌方兵力部署[3]进行估计是战术辅助决策的一个重要环节。每次作战前,我方侦察分队可以侦察到敌方部分兵力,还有一部分兵力则不能被侦察出来。兵力部署估计[4~6]可以根据已侦察出来的敌方兵力情况,预测出敌方未被侦察出来的兵力的位置及属性。
2 兵力部署估计问题阐述
2.1 兵力部署估计模型
完整的兵力部署估计模型原理流程图如图1所示。
侦察分队侦察总结出侦察信息后,系统首先进行规范化方便计算机进行处理。针对规范化的侦察信息,系统进入兵力聚合模块,对一个个作战实体进行分群和识别,即实体聚合和属性估计,最终形成各个作战群体。兵力聚合模块得到的输出再作为兵力部署估计模块的输入,由已知的侦察信息估计敌方在其他地域可能的配置,在理想情况下该配置信息对应于概率最大的数个兵力部署方案。最后经过经验模板筛选和地形模板筛选,输出当前战场上实际的兵力部署估计结果。
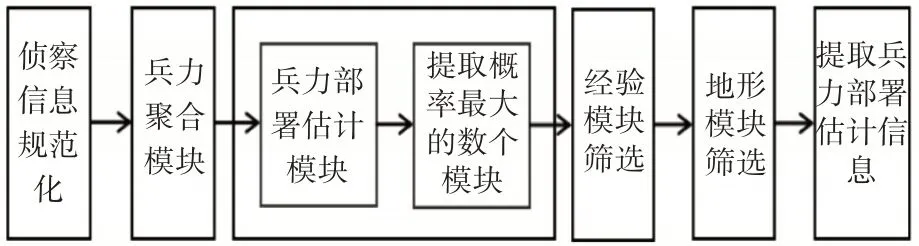
图1 兵力部署估计模型原理流程图
2.2 兵力部署估计方法
兵力部署估计的目标是为了找出未被侦察到的兵力部署的位置和可能的属性。以兵力聚合的分群解释作为输入,其属性包括群体名称、群体类型、群体位置(横坐标、纵坐标)、跨度、可信度,构成的特征向量如下:
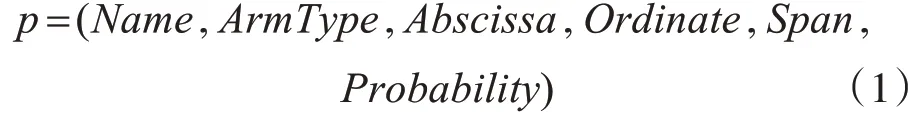
兵力部署估计方法的核心思路是:
1)首先建立兵力部署模板库,该库中的每一个模板包含各个群体的构成信息和(相对)位置信息;
2)接着将兵力聚合后的分群解释输入兵力部署估计模块,与模板库中的模板一一匹配,得到一系列匹配得分;
3)提取得分最大(即概率值最大)的数个模板作为结果输出;
4)模板中各群体的拓扑关系,即是所有侦察到和未被侦察到的兵力间的拓扑关系,由模板可直接推测出未知兵力的位置及属性。
兵力部署估计的方法有如下几种:
贝叶斯网络推理[7]。网络包含两层节点,第一层为N 个证据节点,每个证据节点有两种状态(激活和未激活),第二层为T 个中的1 个兵力部署节点,每个兵力部署节点对应一个兵力部署模板。每一个证据节点与部署节点间存在一个条件概率表,该表包含对应证据在激活与未激活的条件下各模板发生的条件概率。
动态矢量匹配[8]。该方法将各群体之间相互的拓扑关系提取出来,组合后形成兵力部署模板库,通过群体间矢量的匹配来进行防御轴线偏转角计算、群体属性估计及模板匹配。
图神经网络[9]。将每个兵力聚合得到的作战群体看作是图的一个节点,多个作战群体构成一张图,进而模板匹配问题转化为图匹配问题。两张图作为图神经网络的输入,经过学习得到模型参数,对于新来的侦察群体图,经过和所有模板图进行匹配,得到得分最高(完全匹配)的数个模板。
动态矢量匹配的方法虽然可以解决贝叶斯网络方法无法处理群体属性未知的情形,但同样存在一些不足。例如输入群体和模板群体的对应,会在群体属性重复情况下失效,即无法处理有多个同属性群体的情况;矢量的计算对矢量模长敏感,输入群体的相对距离与模板群体的相对距离有尺度的缩放关系,尺度发生改变匹配结果有可能产生很大改变;完全不确定属性的群体的属性估计依赖待选属性的人工选择,必须在计算量和准确度之间折中等等。而图神经网络的方法可以有效解决上述问题。
本文采用图神经网络中的SuperGlue[10]进行图匹配,进而进行兵力部署估计。
3 SuperGlue基本原理
3.1 图神经网络
传统的深度学习方法被应用在提取欧氏空间数据的特征,而新兴的图神经网络则被提出用来处理传统方法处理不佳的非欧式空间,包括节点分类、链接预测和聚类等任务。
图神经网络的研究与图嵌入或网络嵌入密切相关。图嵌入旨在通过保留图的网络拓扑结构和节点内容信息,将图中顶点表示为低维向量,以便使用简单的机器学习算法进行处理。图嵌入与深度学习的结合即是图神经网络。
图神经网络包括,图卷积网络(Graph Convolution Networks,GCN)[11]、图注意力网络(Graph Attention Networks)[12]、图自编码器(Graph Autoencoders)[13]、图生成网络(Graph Generative Networks)[14]和图时空网络(Graph Spatial-temporal Networks)[15]。
3.2 Super Glue的框架及原理
SuperGlue 由Paul-Edouard Sarlin 和Daniel DeTone 于2020 年提出,是一种基于图卷积神经网络的特征匹配算法,它的输入是两张图像中的特征点及描述子(手工特征或者深度学习特征均可),输出是图像特征之间的匹配关系。原论文中Super-Glue用于图像配准环节中的第二步,根据特征描述符找到最佳匹配的关键点。其特点有如下几项:
1)构建了一个可学习的特征匹配器;
2)利用SuperPoint[16]计算得到关键点与描述子;
3)关键点编码,将关键点的位置∕坐标嵌入到具有多层感知器(Multilayer Perceptron,MLP)的高维向量,再与对应的描述子进行融合;
4)多 头 注 意 力 机 制[17],其 中 自 注 意 力 层(self-attention)用于提升局部描述符感受野,交叉注意力层(cross-attention)用于提升两图特征信息交流;
5)最优传输优化匹配[18],将两组学习后的特征向量进行矩阵运算得到得分矩阵S,对得分矩阵采用Sinkhorn[19]算法,求得最优的分配矩阵P,然后根据分配矩阵得到最佳匹配的关键点。
SuperGlue 的大框架是将局部特征点匹配转化为可微最优传输问题。如图2 所示,框架由注意力图神经网络和最佳匹配层组成。
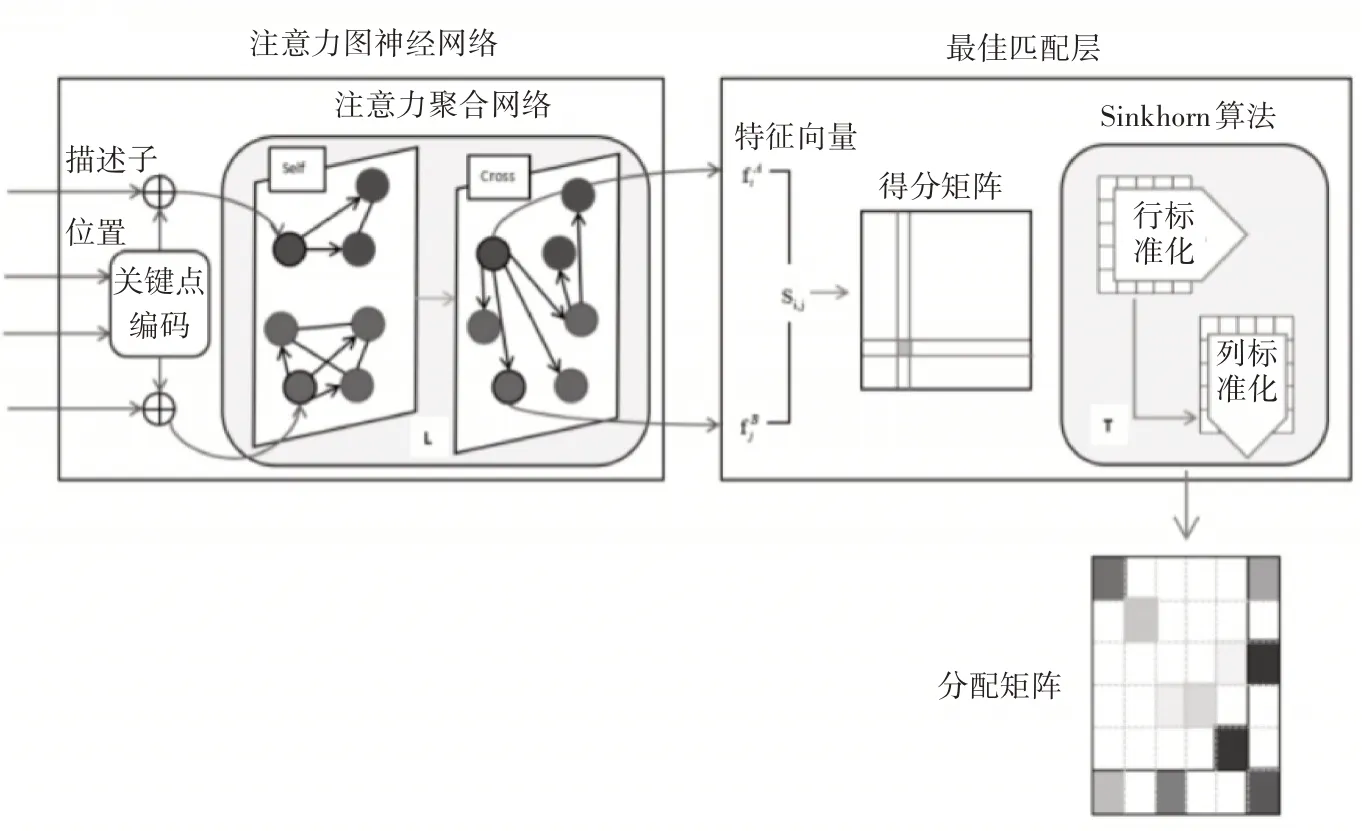
图2 SuperGlue架构
3.2.1 注意力图神经网络
注意力图神经网络(Attentional Graph Neural Network,AGNN)使用关键点编码器将关键点位置p 及其视觉描述符d 映射到高维向量中,然后使用交替的自注意力层和交叉注意力层(重复L 次)来创建更强大的描述信息f 。
关键点编码。特征点位置及描述子合并成每个特征点i 的初始表示为(0)xi,其中位置信息借助高维感知器嵌入到一个高维向量中:
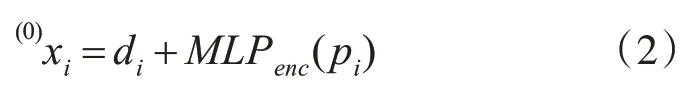
上式将视觉外观和特征点位置进行耦合,使得后续的注意力机制能够充分考虑特征的外观和位置相似度。
注意力聚合网络。该网络中的图C 是是由原始的图A 和图B 组合成的超图。其中的边有两种:一种连接图A 或图B 内部的特征点,εself(self edge);一种连接图A 和图B 之间的特征点,εcross(cross edge)。令lxiAorB表示图A 或图B 上第i 个特征点在第l 层的中间表达形式。令mε→i表示通过自注意力和交叉注意力,聚合与它相邻的所有特征点{ j:( i,j )∈ε} 后,得到的信息(message)。从第l层到l+1层的更新方式为,当前特征点的描述符加上,经过聚合的特征点进行感知器处理后的更新信息。其更新公式如下:
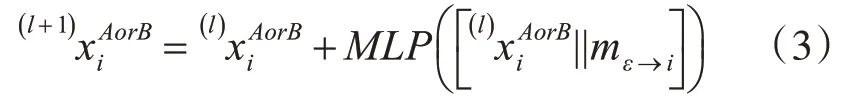
其中,ε ∈{εself,εcross}。
这里交替进行自注意力和交叉注意力聚合,仿佛在模拟人类来回匹配浏览的过程。其中自注意力使特征更加具有匹配特异性,交叉注意力为这些具有特异性的点做图间特征相似度的比较。
线性投影。经过L 次网络计算的描述符再经过一个线性投影,得到最终进行匹配的特征向量:

3.2.2 最佳匹配层
最佳匹配层(Optimal matching layer)创建一个M×N 的得分矩阵,然后使用Sinkhorn 算法(对于T次迭代)解算出最优特征分配矩阵。即最佳匹配层在进行最优传输问题求解。
最优传输问题。根据最优传输理论,对于两组特征点和,其中μs和μt分别表示X 和Y中点的重要程度,pts和ptj为概率∕权重,δ(·)为激活∕脉冲函数。然后定义损失矩阵(Cost Matrix),代表从xi到yj匹配需要的代价:Mi,j=dist( xi,yj)。局部特征点匹配问题转化为

Sinkhorn 算法。对于得分矩阵,先逐行做归一化,再逐列做归一化,重复以上缩放过程N(N>2)步,得到分配矩阵。该算法能够以一种迭代的方式求解最优传输问题。
4 基于SuperGlue的兵力部署估计
进行兵力部署估计时,输入为兵力聚合的输出。由式(1)可知,关键信息为位置信息,包括横坐标(Abscissa)、纵坐标(Ordinate)、跨度(Span)和特征信息,包括群体类型(ArmType)、可信度(Probability)。特征点的位置信息则是3 维的位置向量。对于有D 种群体类型的模板库,可进行one-hot 编码得到D维属性向量,各维的值即是对应群体类型的可信度∕概率值。这两者正好可以作为SuperGlue输入的特征点位置和描述子。
4.1 数据准备
基于已知的T 个模板,建立相应的T 个模板图。每个模板图的坐标向量间的拓扑关系代表典型的阵型。各节点的特征向量由该节点类型的one-hot编码得到。
训练所用数据集由模板图变换得到。包括位置型变换:平移、镜像、旋转和伸缩;特征型变换:掩藏节点、分散可信度;混合型变换:位置型变换和特征型变换的组合。特征型变换中,掩藏节点得到的图相当于战场上有未被侦察的作战群体的情形;分散可信度得到的图相当于战场上某个特定的作战群体属性存疑或未知。
4.2 特征点编码
位置向量(节点的坐标向量)和属性向量(节点的特征向量)在进行耦合前,位置向量会经过多层感知器嵌入到高维空间。该多层感知器的层数和每层的维数作为超参数需要进一步评估。在耦合时,还应当加入权重项λ 平衡二者的重要程度,公式如下:
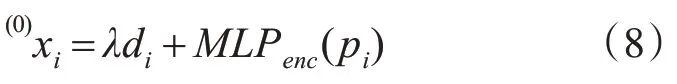
4.3 注意力聚合
注意力聚合网络中,若把一次自注意力和交叉注意力交替作为一层,该网络的深度L 对训练和测试的影响有待进一步评估。
4.4 预测与统计
由分配矩阵可得到图A 与图B 间节点的匹配关系。完配:图A 与图B 间节点的匹配关系全部准确。未配:图A 中的节点在图B 中存在对应关系,但分配矩阵没有匹配结果。错配:图A中的两个节点均在图B 中有对应关系,但分配矩阵得到的匹配结果却是交叉匹配。1 未配:有一个节点未配,其他都配对正确。1 错配:有一对节点错配,其他都配对正确。完配率:完配的图数占图总数的百分比。1 未配率:1 未配的图数占图总数的百分比。1错配率:1错配的图数占图总数的百分比。
由于深度学习的各种原因,得到百分百准确率的结果是一件非常严苛的事情。故仿真实验中允许存在一定程度的未配和错配。
4.5 损失函数
注意力图神经网络和最佳匹配层都是可微的,这使得反向传播成为可能。网络训练使用监督学习,图A 与图B 构成的真值匹配矩阵作为学习目标,最小化分配矩阵P的负对数似然函数。
5 仿真实验及结果
实验基于Python 3.9.7 和PyTorch 1.10.1 实现。人工编辑8 个模板,5 种混合型变换,随机实现10次,共400 个数据图。按8:2 比例分为320 个图的训练集和80个图的测试集。
分别进行了三组对照实验,比较编码维数kens、网络层数gnns、权重项alpha对结果的影响。
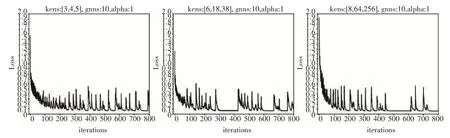
图3 编码维数的对比实验
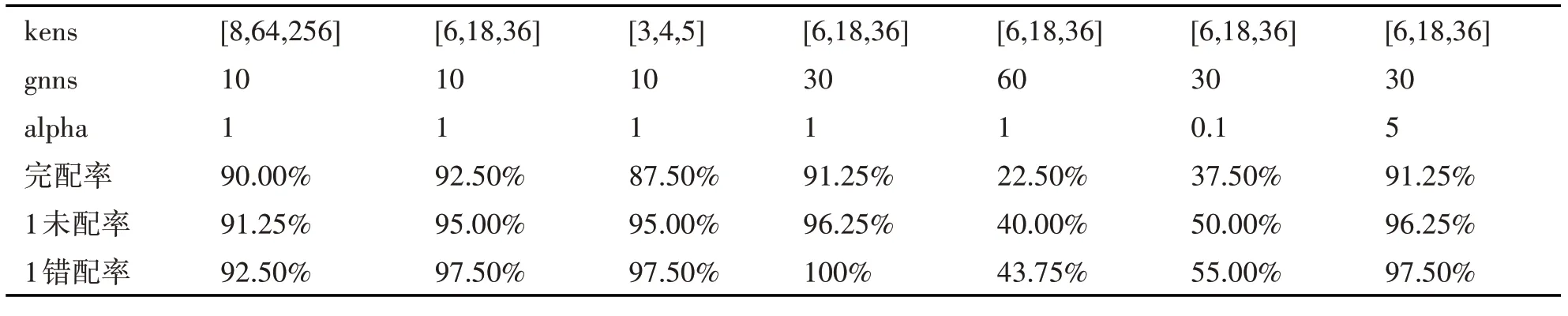
表1 不同超参数下的预测效果
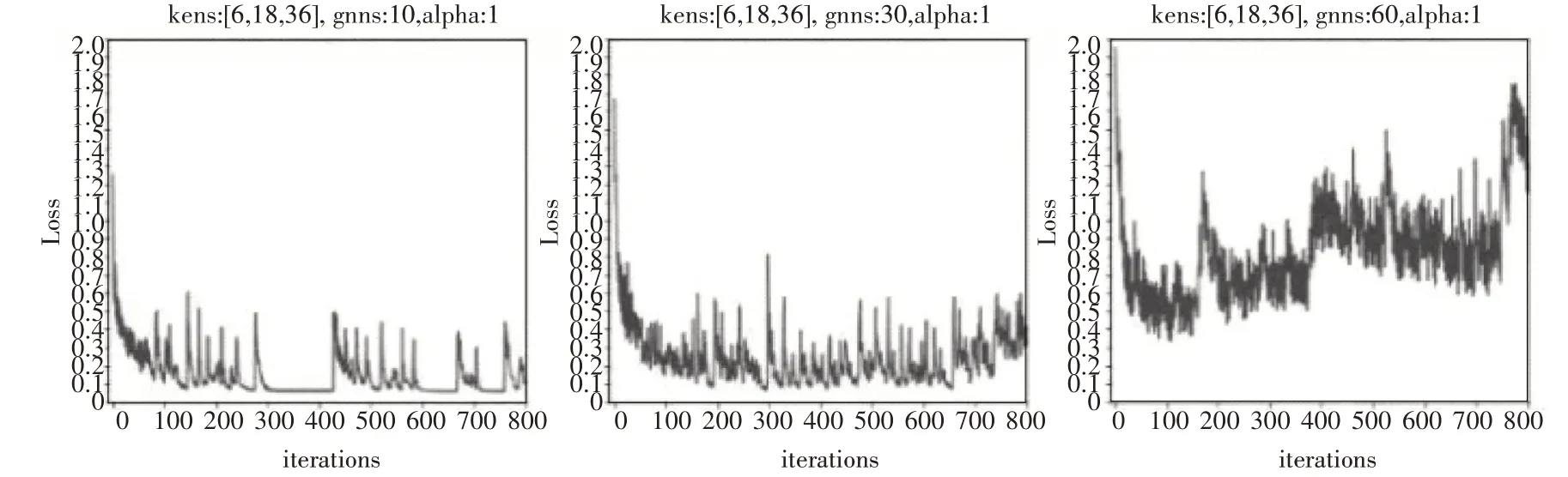
图4 网络层数的对比实验
从图3 中可以看出,编码的维数太低,损失波动较大,效果会略逊一些;编码维数增高,效果相对会好一些。但整体收敛在差不多的范围。可见,编码维数应当稍微高一些,让位置信息映射到较高的高维空间;编码维数并不影响收敛范围。
从图4 中可以看出,随着网络层数的增加,收敛效果越来越差。一种可能的解释是特征向量本身的维度并不高,应当选择适合该维数的深度,过深的网络只会造成学习的饱和。同时随着网络的加深,优化时间也会大大增加,影响学习性能。
从图5 中可以看出,权重项alpha 为1 的时候,收敛效果最好。可见,本目标的学习内容不适合调动该参数。
表1 是上述七个模型参数对应的预测效果。由表一可知,kens=[6,18,36],gnns=30,alpha=1 的模型预测效果最好。增加网络层数到一定深度和降低属性向量权重到一定值都会导致预测效果显著下降。
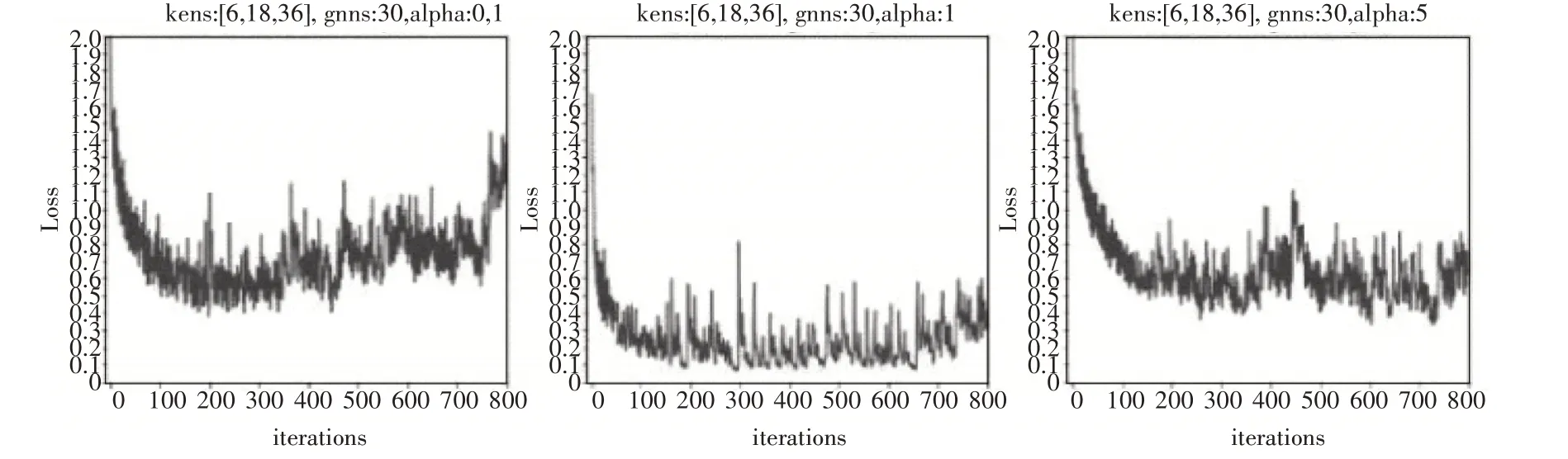
图5 权重项的对比实验
6 结语
本文提出了通过SuperGlue进行兵力部署估计的方法。通过以上仿真实验结果可以看出,该算法可以有效匹配模板,发现原群体阵型中未知的兵力情况和估计不确定属性群体的属性。仿真实验中仅考虑了模板存在的匹配情况,因此不存在于模板库中的新阵型匹配将是本模型需要进一步关注的对象。

