一类新高考数学开放题的命制设计——以一道解三角形题为例

丁亚茹 刘小辉

(福建省集美大学 361021)

1 问题提出

为突出对学生综合能力和学科素养的考查，新高考新增了多项选择题、逻辑题、数据分析题、举例题及开放题等新题型.任子朝在高考新题型测试研究中提出，开放题作为新增题型，能够很好地考查学生的逻辑思维能力与应用意识，也更加契合高考作为选拔性考试对区分度的要求.

实际上，数学开放题早在20世纪70年代便引起了国内外学者的关注，数学开放性试题突破固有的解题模式，侧重考查学生综合运用知识的能力和“执果索因”的思维方式.新高考试题的命制要增强开放性和灵活度，充分发挥高考命题的育人功能和积极导向作用，减少识记类题型的命制，增加开放探究类题型的比重.

2 封闭数学题的命制结构

以“解三角形”为例，在试题命制中通常会结合三角函数、三角恒等变换的知识，目的在于考查学生对知识的综合应用及学科核心素养，本题型常以两小问的形式出现，试题的设置具有层次性.

题目(2018年全国卷第17题)在平面四边形ABCD中，∠ADC=90°，∠A=45°，AB=2，BD=5.

(1)求cos∠ADB；

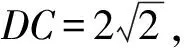
传统题目的结构一般是由条件、策略和结论三方面构成，其特征是条件完备，策略清晰，结论确定.由封闭题的结构及特征出发，将其改造为开放题，可以有效地改变学生解题的思维定势，培养学生的创造性思维.

3开放题命制设计——从封闭走向开放

我国的戴再平先生根据未知的要素将开放题划分为四种类型：条件开放型、策略开放型、结论开放型以及综合开放型；美国的Silver教授将开放题分为条件开放、最终结果开放、解题过程开放以及三种类型的综合情况.结合封闭题的结构特征，命题者还可以从单一开放型和综合开放型两大类出发进行改造.本文以2018年全国卷第17题解三角形为例，研究单一开放型和综合开放型两种命题模式.

3.1 单一开放型

3.1.1 条件开放型

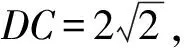
3.1.2 策略开放型

命制题目时可与新定义题型相结合，如将题目第二问改为：以点D为圆心，DC为半径画圆，交DB于点E，DF=kDC，给出定义：若从三角形一个角出发向对边作一条线段，该线段刚好平分此角，则称该线段为三角形的“吉祥线”.问：当DF为△BCD的“吉祥线”时，求k的取值范围.题目将角平分线定义改为 “吉祥线”定义，知识点简单，主要考查学生的转化思想.在解题策略上，一般采用常规解三角形的方法求解，而擅长几何的学生又可以运用几何法求解，这样不同水平的学生可以从不同的维度去揣摩问题，获得不同的见解.

3.1.3 结论开放型

3.2 综合开放型

综合型开放题将从条件与策略双开放型以及条件与结论双开放型两种情况入手进行改造，有助于考查学生思维的延展性及全局性.

3.2.1 条件与策略双开放型

条件与策略双开放型可进行两种设计，一种是选择条件，策略不同，结论固定，另一种是补充条件，策略不定，结论固定.

第一种设计可依据2020年北京卷第17题进行改造：以∠ADC=90°为前提条件，将其他条件分类并组合供学生选择，

条件①：AB=2，BD=5，AD=8；

条件②：∠A=45°，AB=2，BD=5；

学生解答时若不进行筛选和判断信息而直接选择条件①，则未考虑到三角形的存在与否.进行筛选后的学生若选择条件②，运用正弦定理即可求解，此时要注意角的范围.若选择条件③，可以运用余弦定理，但计算量较大且易出错.题目考查的知识点较简单，但每一个设计都有所不同，有助于区分不同层次的学生.

第二种设计可将题中条件进行挖空处理，让学生自行补充，提升学生发散性思维能力，解题过程也不再是千篇一律.如将本题中的条件∠A=45°隐去，此时可给定策略，如要求学生运用正弦定理求解，这样能更精确地考查学生对知识点的掌握情况，或在结论固定的前提下要求学生补充，这样设计更加灵活，策略也更加多样.

3.2.2 条件与结论双开放型

条件与结论双开放型在设计时可提供多个条件供学生选择，选择条件不同，结论不同，如2020年新高考卷第17题，以此为参照将封闭题进行改造：

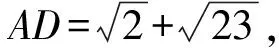
学生选择条件②时，可采用余弦定理求解，条件①则为干扰项，选择条件③时，学生可通过正弦定理求解.

4 结论与建议

4.1 从封闭到开放题的命制路径

一道题目由条件、策略以及结论三方面构成，通过对这三方面的不同开放方法，设计一种由封闭题转变为开放题的命制路径.上述改造方式可以总结为图1.

4.2 开放题设计建议

4.2.1 强化开放题在教学过程中的应用性

数学教师应该注重对开放题的命制研究，在命制试题的实践中提升自身的专业能力.在教学过程中，要注重开放题与学科知识的整合，有效改进教与学的方式，如课堂导入环节可以以开放题为背景，快速抓住学生注意力，引出新课题；在新知传授环节，要有意识地向学生展现多样化的开放型试题，丰富课堂教学的素材，满足不同学生在数学上的不同需求，真正做到因材施教.因此，教师应该在教学中潜移默化地渗透开放题思维，促使学生由接受到熟悉再到灵活求解开放题，发展学生学科核心素养.

4.2.2 发挥学生在开放题设计过程中的主体性

教师可带领学生共同设计开放性试题，学生不再是被动的解题者，而是参与到试题命制的设计者，共同命制的过程既发挥了教师的主导作用，又体现了学生在学习中的主体地位.针对基础薄弱的学生，教师可以引导他们命制自己认知领域内较简单的题目，及时给予肯定，使学生乐意并积极投入到试题的命制中，帮助他们重拾学习数学的信心，提高学习数学的兴趣；对于数学兴趣浓厚的学生，教师则可以鼓励他们命制丰富多样的题目，解决了优等生“吃不饱”的现象.试题中蕴含着丰富的知识，教师要引导学生在命制中思考，在思考中命制，实现对知识的意义建构，拓宽探索空间.不同层次的学生设计出多样化的试题，共同参与探讨和交流，这一过程将会给学生带来全新的学习体验，让学生在参与中深度理解、有效创新.

4.2.3 注重开放题改造在高考中的可操作性

为保证高考阅卷的高效准确，开放题需要在题目开放性和阅卷工作量上寻求平衡.开放性过强往往会导致阅卷困难，也不利于分层，这就无法保证阅卷的高效性；开放性不宜过低，否则无法保证开放题发挥应有的功能.其次，开放题的评分标准要具有科学性，处理好区分性和统一性的关系.具有区分性的评分标准体现开放题的区分功能，具有统一性的评分标准保证开放题在高考中的公平性和实施性.再者，受学生认知发展和已有经验的限制，高考试题应以传统封闭题为主，开放题为辅，逐步过渡.开放题的创新性特点也要求其起点要放低，注重考查学生对知识的灵活应用.故开放的形式以及程度需要把握好度，这是今后研究需要进一步改进的方向.