BDS-3多频PPP模型性能分析

吴志远 王潜心 胡 超 武 威

1 中国矿业大学环境与测绘学院，江苏省徐州市大学路1号，221116 2 安徽理工大学空间信息与测绘工程学院，安徽省淮南市泰丰大街168号，232001

与BDS-2相比，BDS-3不仅解决了BDS-2卫星观测值中的伪距偏差问题[1]，并且在原有的B1I和B3I频率基础上新增B1C、B2a、B2b和B2等4种新频率，其中B1I和B3I信号的调制方式也有所不同。多频信号可用于电离层延迟消除、周跳探测和模糊度固定等，尤其在PPP的相关研究上存在许多潜在优势。由于前期BDS-3的建设不够完善，在轨卫星数量较少、能同时接收到B1C、B2a和B2b三种新频率的测站数量有限，因此针对BDS-3卫星播发新频率的PPP定位效果的研究较少。本文针对BDS-3卫星播发的新频率进行三频PPP相关研究，包括静态和仿动态2种模式。首先在原始观测方程的基础上推导出常用的三频PPP数学模型，即非差非组合模型、消电离层模型和无电离层组合模型，并对新频率组合模型中出现的偏差和改正进行详细分析[2]；然后通过MGEX测站数据分别比较B1I和B3I的双频非差非组合模型(DU2)、B1C和B2a的双频非差非组合模型(DU3)、基于B1C、B2a、B2b的三频非差非组合模型(TU)、三频消电离层模型(TF)和三频无电离层两两组合模型(TDF)的定位性能；最后总结BDS-3新三频PPP定位性能，为未来的北斗多频定位相关研究提供参考依据。

1 三频PPP函数模型

三频原始伪距和载波相位的基本观测方程为：

(1)

现定义：

(2)

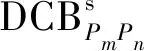
由于卫星钟差dts与卫星端UCD线性相关，因此无法将两者直接分离，需要引入精密卫星轨道和钟差改正。一般采用IGS组织播发的基于B1I/B3I无电离层组合观测值估计的产品进行改正[5]：

(3)

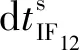
引入精密卫星轨道和钟差改正，将式(3)代入式(1)并线性化得：

(4)

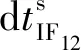
(5)

与传统模型不同，由于三频PPP的前2个频率并不是B1I和B3I，因此DCB的值和无电离层组合因子也有所变化。改正后的观测方程为：

(6)

1.1 非差模型(TU)

TU模型不对三频数据作任何线性组合，而是直接使用原始伪距和相位观测方程，即

(7)

(8)

将式(8)代入式(7)并重新规划参数：

(9)

式中，IFBr,j为j频率上的伪距频间偏差，且

(10)

1.2 消电离层模型(TF)

TF模型是将三频数据组合成消去电离层一阶项的观测值，即

(11)

式中，

(12)

组合系数e1、e2、e3需满足[6]：

(13)

1.3 无电离层两两组合模型(TDF)

BDS-3三频数据能够组合产生2个双频无电离层组合(B1C/B2a和B1C/B2b)[7]，组合后的观测方程为：

(14)

式中，IFBr,IF13为无电离层两两组合的伪距频间偏差参数，且

(15)

1.4 BDS-3新三频PPP特点

为研究BDS-3卫星新三频PPP的定位性能，采用BDS-3卫星2种双频非差非组合模型DU2和DU3进行对比。BDS-3卫星的双频、三频PPP模型特点见表1，不同的模型采用不同的频率和组合系数，需要注意不同模型的卫星端DCB改正。

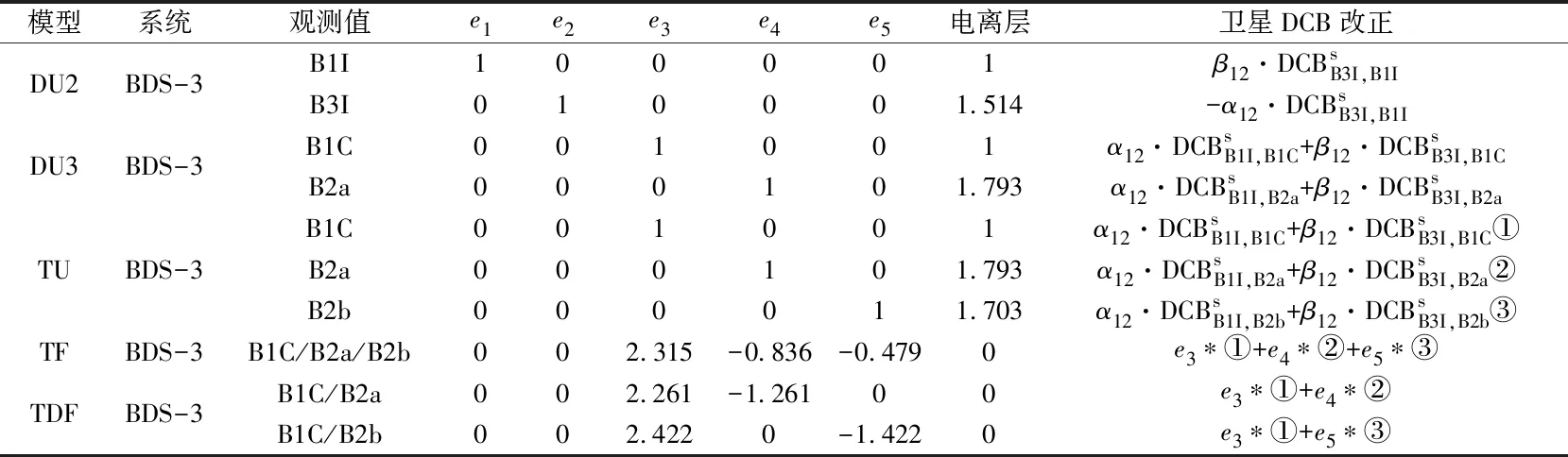
表1 BDS-3双频、三频PPP模型特征

2 三频PPP随机模型

对于多个频率的观测值，通常将其方差量化为与卫星高度角、信噪比有关的函数形式[8]。本文基于卫星高度角的随机模型将观测值噪声σ模型化为卫星高度角E的函数[9]，即

(16)

式中，a和b是常数。对于原始载波相位观测值噪声σL,a和b均设为0.003 m；原始伪距观测值σP设为载波相位观测值的100倍，即a和b取0.3 m。假设多个频率的观测值之间相互独立且伪距噪声值也相同，则载波相位观测值噪声与频率无关，因此σP1=σP2=σPn,σL1=σL2=σLn。

根据误差传播定律可得三频非差非组合模型(TU)、三频消电离层模型(TF)、三频无电离层组合模型(TDF)对应的方差协方差矩阵为：

(17)

3 实验结果分析

3.1 实验数据及解算策略

选取14个MGEX测站2021-09-01～10的数据，采样间隔为30 s，所选测站均能接收到BDS-3卫星播发的新频率B1C、B2a、B2b信号。

分别以静态、仿动态2种定位模式从定位精度和收敛时间方面对比DU2、DU3、TU、TIF和TF等5种PPP模型的定位性能。以IGS提供的SINEX文件中的坐标为真值，当测站的E、N、U方向上的绝对定位误差连续60个历元(30 min)均小于0.1 m时判定为收敛。新频率B2b的卫星端DCB改正值采用MGEX提供的DCB文件中的C7Z类型，联合使用Geometry-Free和Melbourne-Wubben组合对周跳进行探测修复[10]，具体PPP数据处理策略见表2。

表2 数据处理策略

3.2 静态PPP实验

图1为ENAO和MET3测站在doy244的5种PPP模型静态定位误差曲线。由图可见，DU2模型的定位效果最差，尤其是在U方向上。

图1 5种PPP模型静态定位误差

图2为14个测站5种PPP模型doy244～253静态定位结果的平均偏差和收敛时间及其平均值，图3为5种PPP模型三维收敛时间和定位精度。由图2可见，除个别测站外，相对于DU2模型，新双频DU3模型和三频PPP模型在三维定位精度和收敛时间上均有所提升，其中U方向上的精度提升最大。5种模型的平均定位精度和收敛时间见表3。由表可见，相比于传统的DU2模型，DU3模型在收敛时间和E、N、U方向上的定位精度分别提升9.4%和8.4%、0%、35.8%；TU模型分别提升14.9%和14.2%、4.6%、40.2%；TDF模型分别提升16.7%和21.2%、13.7%、42.7%；TF模型分别提升16.0%和18.6%、13.7%、42.2%。综上所述，三频PPP模型的定位效果略好于新双频DU3模型，其中TDF模型的精度最优。

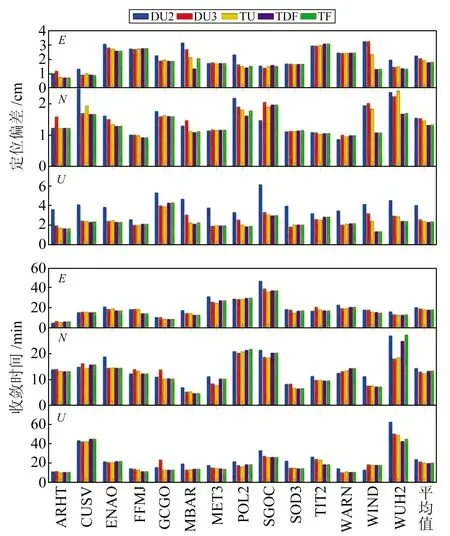
图2 14个测站5种PPP模型静态定位偏差和收敛时间平均值

3.3 动态PPP实验

图4是ENAO和MET3测站在doy244的5种PPP模型动态定位误差曲线。与静态定位相同，三频PPP模型和DU3模型在收敛时间和定位精度上均有所提升，但不同的是，动态定位中4种模型在收敛时间上的提升效果较为明显。

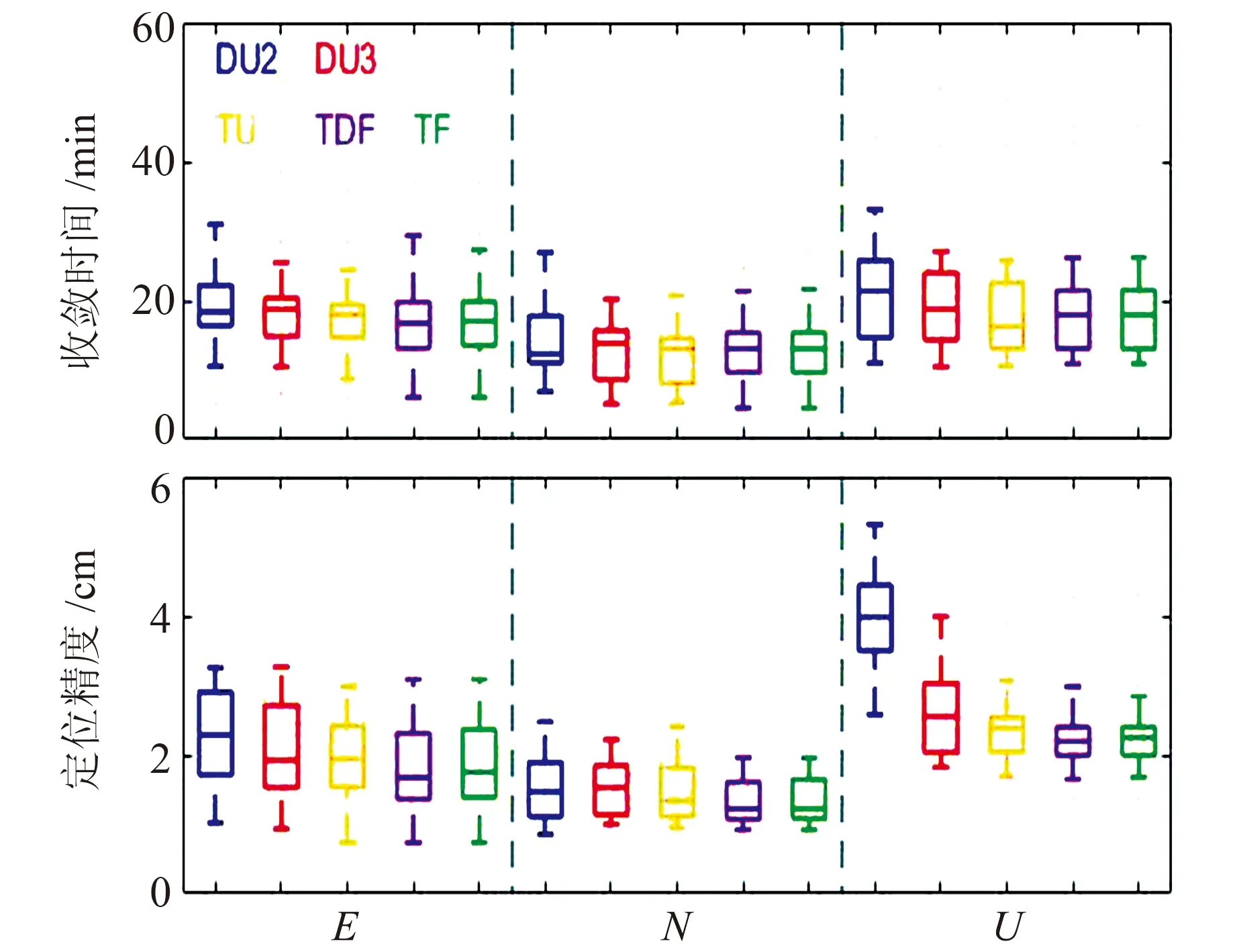
图3 5种PPP模型静态三维收敛时间和定位精度

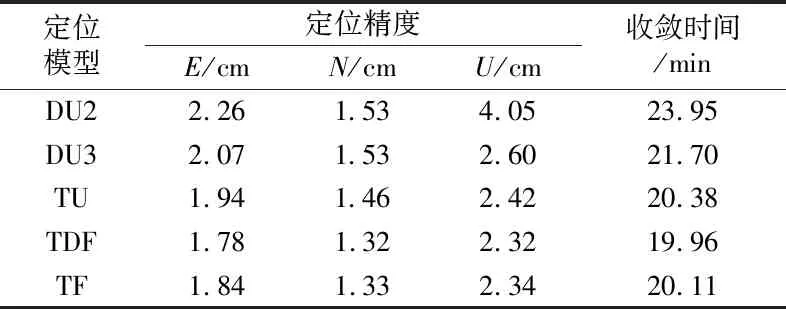
表3 5种PPP模型静态定位收敛时间和精度

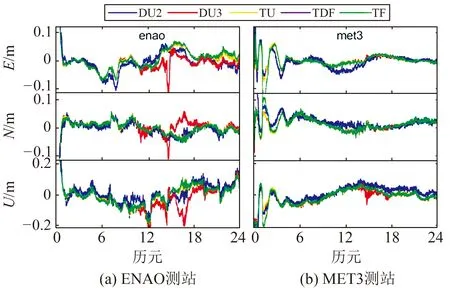
图4 5种PPP模型动态定位误差

图5为14个测站5种PPP模型连续10 d动态定位结果的平均偏差和收敛时间及其平均值，图6为5种PPP模型三维收敛时间和定位精度，表4为5种模型的平均定位精度和收敛时间。可以看出，相比于传统的DU2模型，DU3模型在收敛时间和E、N、U方向上的定位精度分别提升12.2%和20.1%、8.8%、13.5%；TU模型分别提升15.6%和32.6%、26.5%、27.7%；TDF模型分别提升16.9%和35.6%、30.4%、29.9%；TF模型分别提升17.2%和30.4%、25.8%、29.1%。综上所述，三频PPP模型的动态定位效果强于新双频DU3模型，其中TDF模型在定位精度上的提升效果最明显，TF模型对收敛时间的提升效果最好。

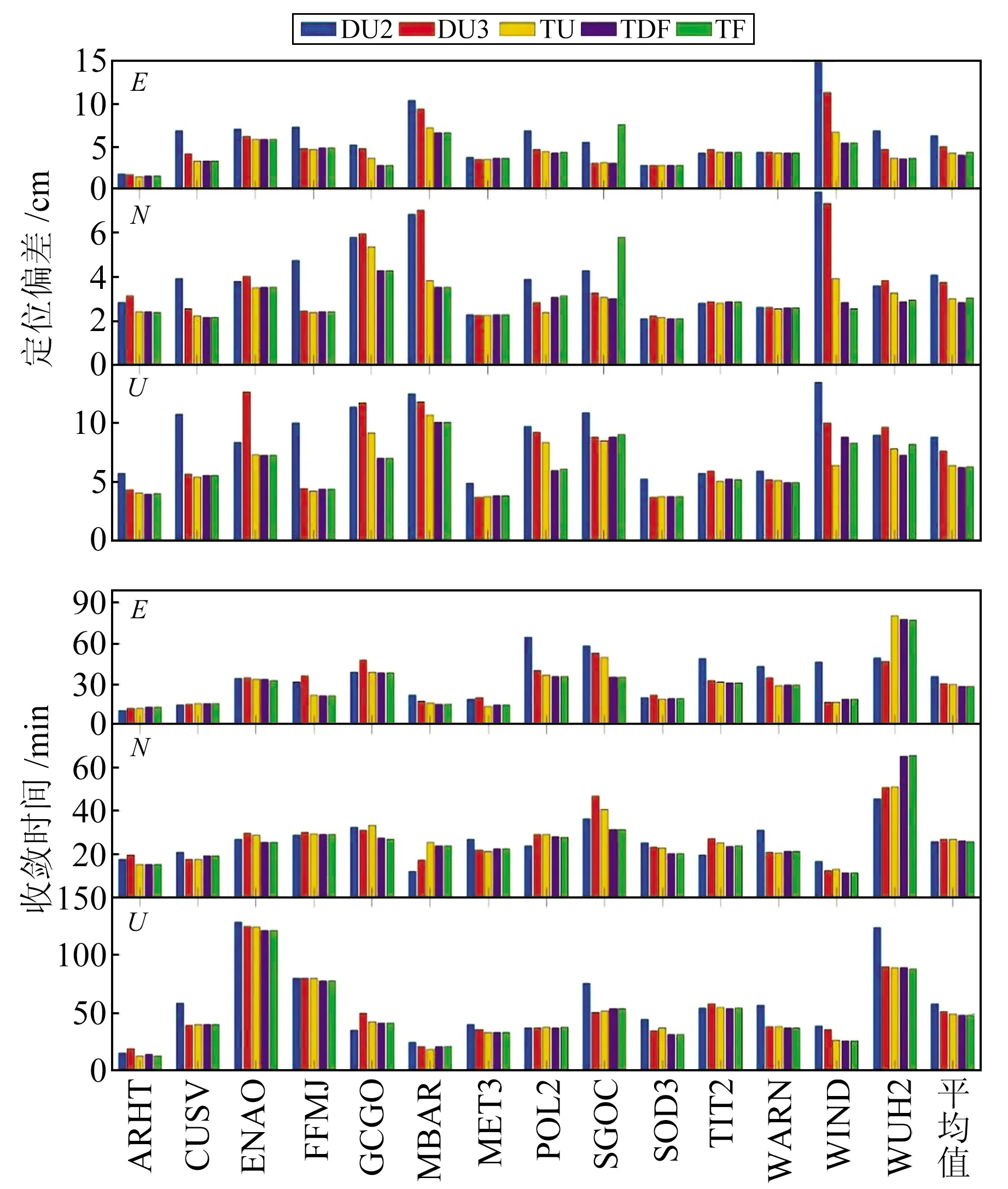
图5 14个测站5种PPP模型动态定位偏差和收敛时间平均值

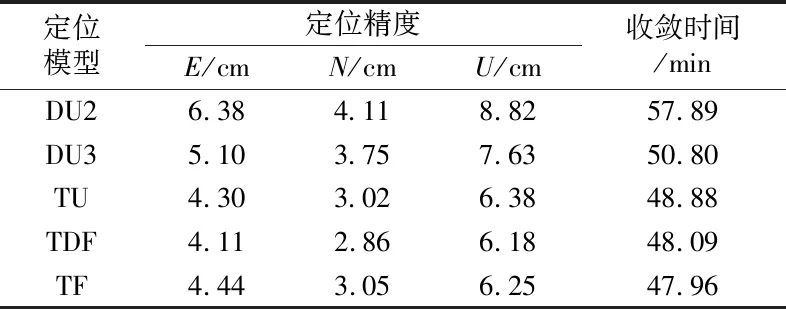
表4 5种PPP模型动态定位收敛时间和精度统计

4 结 语

1)BDS-3的DU2模型在静、动态定位中的收敛时间分别约为24 min和58 min；而B1C、B2a和B2b新频率组成的双频非差非组合模型和三频PPP模型在静、动态定位中的收敛时间可达约20 min和50 min，三维定位精度能达到2 cm和7 cm，提升较大。

2)与传统B1I/B3I双频DU2模型相比，DU3、TU、TDF和TF模型的定位性能均有所提高。在收敛时间方面，TDF模型对静态定位的提升最大，略高于TF模型；TF模型对动态定位的提升最大，略高于TDF模型。在定位精度方面，TDF模型对静态和动态定位的提升最明显。

本文对于北斗三号卫星新三频PPP模型的性能分析仅限于模糊度浮点解，在北斗多频同时播发的条件下，PPP模糊度固定解具有更加广阔的应用前景。在后续研究中，笔者将着重研究北斗多频模糊度固定技术方法。