角度及频率变化率量测下目标运动分析的可观测性条件*

余 银，周 彬，李银波，刘永旭，吴启星

(1.电子信息控制重点实验室，成都 610036；2.北京跟踪与通信技术研究所，北京 100094)

0 引 言

目标运动分析(Target Motion Analysis，TMA)主要指利用无源探测方式，由一段时间的量测信息对目标的运动状态进行估计，包含对目标位置、速度、加速度及高阶运动信息的估计[1-3]。目标运动分析可观测性是指目标运动状态估计的唯一性[4]。可观测性是对目标运动分析的前提，但目标运动分析多为非线性系统问题。非线性系统可观测性分析涉及求解高阶非线性微分方程，较难直接应用于目标运动分析的可观测性判别。因此，确定可观测性及获取可观测条件是目标运动分析的难点之一。

目标运动分析的可观测性与量测信息息息相关。单站由于其具有系统简单、适应性强等优点受到了青睐[5-6]，但与多站相比可测性较差，所以对单站目标运动分析的可观测性研究显得尤为重要。仅测角单站目标运动分析是最简单、最经典的方法，至今已有大量文献对该方法进行了研究，并采用不同方法对其可观测性进行了深入分析[1,3,7-12]。仅测角的可观测性要求观测站运动阶数高于目标运动阶数。随后，研究者们致力于引入其他量测信息来改善可观测性。例如，较早期的引入频率[4,13]，以及后来的引入径向加速度[14]、角度变化率[15]、相位差变化率[16]、到达时间[5,13]、频率变化率[1,16]等。

文献[9,17]对现有单站可观测性分析方法进行了总结，后者将单站可观测性分析方法归纳为几何方法、代数方程方法和线性系统方法三类。文献[2-3]将非线性系统转换为线性时变连续系统，利用可观测矩阵进行分析。但该方法涉及求解高阶微分方程，难以用于高阶运动。文献[5,7,15]对非线性系统泰勒近似和离散化，通过离散系统的可观测矩阵进行分析。文献[8,10-12]将非线性量测方程转换为伪线性量测方程，并基于可观测条件的泛函等式进行了分析，避免了求解高阶微分方程。该方法在文献[17]中归为线性系统法。文献[4,18]提出了一种相容轨迹的方法分析目标运动分析可观测性条件。该方法在文献[17]中归为代数方程法。后两种方法适用性广，且无近似处理，可获得可观测性充要条件。

“角度+频率变化率”的单站体制基于运动学原理，理论完备，不需要已知频率，动态性能好，近年来受到了广泛关注[1,19]。频率变化率为高阶微分量，与基于角度、频率、到达时间等信息的可观测性分析相比难度更大，同时相关研究还非常少。本文采用相容轨迹和系统可观测性理论两种方法分别从定性和定量的角度对“角度+频率变化率”的可观测性进行分析，给出可观测性的充要条件，为目标运动分析提供理论支撑。

1 问题描述

如图1所示，目标沿着轨迹rT(t)=[xT(t),yT(t),zT(t)]T运动，观测站沿着rO(t)=[xO(t),yO(t),zO(t)]T(通常已知)运动，r(t)=rT(t)-rO(t)=[x(t),y(t),z(t)]T是目标T相对于观测站O的轨迹，t表示时间。

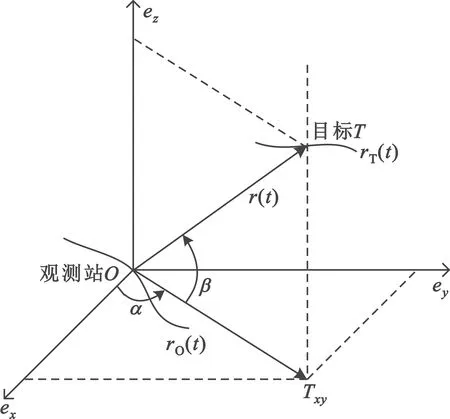
图1 观测站、目标相对关系示意图

观测站接收目标辐射的信号，并从信号中提取量测信息，对目标运动状态r(t)进行估计。如果通过[t0,tf]内的量测信息能唯一确定[t0,tf]内的r(t)，则是可观测的。本文考虑的量测信息包括方位角α(t)、俯仰角β(t)、频率变化率ν(t)下的可观测性分析。根据多普勒效应，ν(t)满足

(1)

2 基于相容轨迹法的可观测性定性分析

2.1 任意目标运动下的可观测性

定义1 给定一组量测量{z(t)|t∈[t0,tf]}，若存在多个不同的目标运动轨迹均满足这组量测量，则称这些轨迹在该组观测量下是相容的。

目标运动分析可观测，当且仅当目标真实轨迹的相容轨迹是自身。

定理1 任意目标运动下，给定一组“角度+频率变化率”量测信息，目标运动轨迹的相容轨迹不唯一。

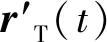
r′(t)=γ(t)r(t) 。

(2)

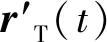
(3)

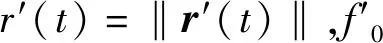
(4)

(5)

式中：M(t)为正交矩阵，∀t∈[t0,tf]。

在{α(t),β(t),ν(t)}量测量下，相容轨迹是式(2)和式(5)的交集，即

(6)

且

(7)

因此，任意目标运动下，总是存在不唯一的相容轨迹，目标运动分析不可观测。

2.2 有限阶目标运动下的可观测性

本节讨论有限阶目标运动下的可观测性问题。有限阶目标运动是指目标运动轨迹可表示为有限阶多项式。具体地，若目标为N阶运动，则满足dNrT(t)/dtN=0，积分可得

rT(t)=a0+a1(t-t0)+a2(t-t0)2+…+aN(t-t0)N≜At。

(8)

定理2 有限阶目标运动下，给定“角度+频率变化率”量测信息，目标运动轨迹不存在相容轨迹当且仅当目标与观测站间存在非径向相对运动。

证明:式(6)可重新整理为

(9)

其次，考虑目标与观测站间存在非径向相对运动的情况。由式(9)可得

(10)

因此，有限阶目标运动下，目标运动分析是可观测的充要条件是目标与观测站间存在非径向相对运动。

3 基于系统可观测性理论的可观测性定量分析

本节采用系统可观测性理论对“角度+频率变化率”的可观测性进行定量分析。首先分析一阶运动下的可观测性，然后推广到任意有限阶的情况。

3.1 系统可观测性理论

考虑一般的线性时变系统：

(11)

式中：x是状态向量，u是输入向量，z是量测向量，A是状态矩阵，B是输入矩阵，C是量测矩阵。

系统(11)在[t0,tf]上是完全状态可观测的是指∀x(t0)在u(t)和z(t)已知的情况下，x(t0)可唯一确定。

根据线性系统理论，系统(11)在[t0,tf]上可观测当且仅当可观测性矩阵O(t,t0)是正定的，其中

式中：Φ(t,t0)称为状态转移矩阵，满足∂Φ(t,t0)/∂t=A(t)Φ(t,t0)且Φ(t0,t0)=I。

上述可观测性条件可进一步转换为引理1[12]。

引理1 系统(11)在[t0,tf]上可观测当且仅当{∀t∈[t0,tf],C(t)Φ(t,t0)y=0}⟹{y=0}成立。

3.2 目标常速运动下的可观测性

(12)

经过计算可得系统(12)的状态转移矩阵为

(13)

角度量测量α(t)、β(t)可表示为

(14)

(15)

定理3 考虑目标常速运动方程(12)和量测方程(14)和(15)，其可观测当且仅当目标与观测站在[t0,tf]存在非径向运动时。

证明：式(14)经整理可转换为伪线性形式：

(16)

此外，考虑到r=xcosβcosα+ycosβsinα+zsinβ，对式(15)进行整理可得

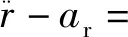
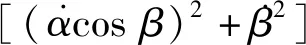
(17)

zcv(t)=Ccv(t)x(t) 。

(18)

(19)

Ccv(t)Φ(t,t0)a=T1Q[a0+(t-t0)a1]。

(20)

针对C(t)Φ(t,t0)a=0，∀t∈[t0,tf]分两种情况进行讨论。

(1)目标相对观测站径向运动

(2)目标相对观测站存在非径向运动

3.3 有限阶目标运动下的可观测性

在常速运动可观测性分析的基础上，本节进一步拓展到有限阶目标运动下的可观测性分析。

N阶运动目标满足dNrT(t)/dtN=0。状态转移矩阵为

(21)

定理4 考虑N阶运动目标(21)和量测方程和(15)，其可观测当且仅当目标与观测站在[t0,tf]存在非径向运动时。

zN(t)=CN(t)x(t)。

(22)

(23)

类似目标常速运动，针对C(t)Φ(t,t0)a=0，∀t∈[t0,tf]分两种情况讨论。

(1)目标相对观测站径向运动

(2)目标相对观测站存在非径向运动

因此，基于系统可观测性理论，可得出角度和频率变化率量测下目标运动分析的可观测性充要条件是目标与观测站间存在非径向相对运动，与前一种方法结论一致。

4 仿真分析

本节分别从相容轨迹和目标跟踪进行仿真分析，验证前面的结论。前者对目标运动阶数无限制；后者考虑有限阶目标运动，建立有限阶目标运动模型，利用扩展卡尔曼滤波[20]进行目标运动分析，获取目标航迹。

4.1 相容轨迹仿真

如图2中实线所示，观测站处于(0,0)km位置，目标从距离观测站80 km、方位角165°出发，沿x方向作匀速直线运动。

图2 相容轨迹计算结果

图2中虚线分别是由距离观测站65 km、70 km、90 km、100 km、110 km不同的起始位置，按照与目标实际运动轨迹在任意时刻具有相同的方位角和相等的距离二阶变化率计算获得的，也即这些虚线都是目标实际运动轨迹的相容轨迹。

由此可知，相容轨迹不是目标实际运动轨迹本身，且存在多条不同的相同轨迹。实际上，任意不同距离的起始位置均可产生一条相容轨迹，即存在无穷多相容轨迹，也即目标运动分析不可观测。

4.2 目标运动分析仿真

本节利用有限阶目标运动模型进行目标运动分析，获取目标的航迹。考虑目标与观测站径向运动和目标与观测站非径向运动两种情况。

径向相对运动：观测站位于(0,0,3)km位置，目标从坐标为(-4,0,3)km的位置沿x方向以200 km/h的速度匀速运动。目标发射的信号载频为8 GHz。

非径向相对运动：观测站位于(0,0,0)km位置，目标从坐标为(-4,1,3)km的位置沿x方向以200 km/h的速度匀速运动。目标发射的信号载频为8 GHz。

建立常速模型，利用扩展卡尔曼滤波分别对两种情况下的目标运动分析进行仿真。方位角和俯仰角测量误差均为0.5°，频率变换率测量精度5 Hz/s。观测时长为144 s，进行100次蒙特卡洛仿真。

图3和图4分别给出了两种情况下的位置估计误差曲线。由图3可知，径向相对运动下位置估计误差曲线发散，而图4中非径向相对运动下的位置估计误差可收敛到较小值，由此验证了前面的理论分析结论。

图3 径向相对运动下的位置估计误差曲线

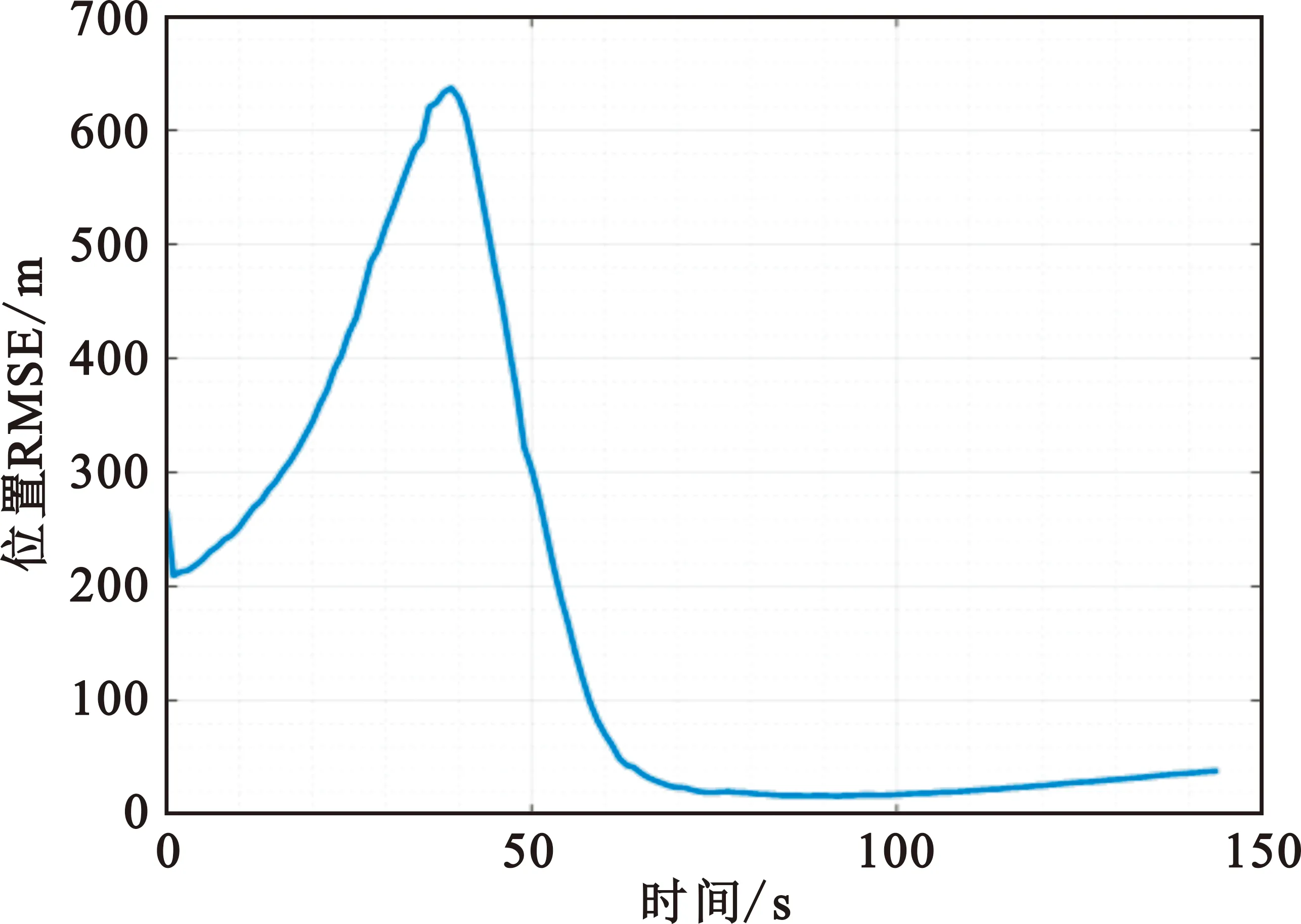
图4 非径向相对运动下的位置估计误差曲线

5 结 论

可观测性是进行目标运动分析的前提。本文采用相容轨迹法和系统可观测性理论分别从定性和定量角度讨论了角度和频率变化率量测下目标运动分析可观测性问题。对于有限阶目标运动，可观测性的充要条件是目标与观测站存在非径向相对运动。仿真分析验证了本文的理论结果。