磁流变离合器非线性迟滞特性试验与建模

王书友，肖鹿，陈飞，孟德远,2，田祖织，李艾民，吴向凡

(1.中国矿业大学机电工程学院，江苏徐州，221116；2.江苏科技大学江苏省船舶机械装备先进制造与工艺技术重点实验室，江苏镇江，212003；3.徐州工程学院机电工程学院，江苏徐州，221018)

磁流变液(MRF)是一种能够响应外磁场而快速可逆地改变其流变特性的智能材料[1-2]。由于其独特的流变性能，它们被开发成各种各样的装置，如MR 阻尼器或MR 离合器。与传统执行器相比，磁流变执行器具有设计简单、控制性能优越和控制消耗低等优点。此外，该执行器能够瞬间且可逆地控制执行器在执行机构中的顺应性。因此，采用磁流变执行器可以有效提高传统控制系统性能。

然而，MR离合器面临着输出转矩和输入电流之间的非线性关系，其固有的非线性滞回特性使其难以建立精确的数学模型。在实际应用中很难实现精确、快速和高效的控制，限制了磁流变技术在工业领域的广泛应用。目前，已有各种描述MR 阻尼器位移/速度与输出力之间关系的建模方法[3-11]，但很少有建立MR 离合器电流-转矩滞回行为的动力学模型。磁流变离合器的电流-转矩曲线中引入了滞环，给控制系统带来跟踪误差、谐波和不稳定[12]。因此，准确地评估这种非线性关系对于有效地控制MR离合器具有重要意义。

MR 离合器中广泛使用的模型主要是静态模型，包括Bingham 模型和Herschel-Bulkley 模型。这些模型将磁流变液的剪切应力与施加磁场联系起来，适合大多数应用中磁流变离合器的分析和设计。但上述2种模型均忽略了磁流变离合器的迟滞特性，难以用于动态分析和控制。为了便于动力学分析，学者在MR离合器模型中引入了参数化模型。AN 等[13]提出了MR 离合器的非线性建模，包括铁磁材料的Hodgdon 模型和MR 流体的Bingham模型，发现将Coleman-Hodgdon模型和非线性Bingham模型相结合可以较好地预测输入电流和输出转矩之间的非线性关系；JEDRYCZKA等[14]将Jiles-Atherton 模型引入MR 制动器的迟滞行为中，发现所提出的迟滞模型能较好地描述电磁和磁流变耦合效应的行为；YADMELLAT 等[15]在以MR 离合器为基础的执行机构中引入了Preisach 模型，发现Preisach 模型基本可以描述MR 离合器的电流-转矩曲线；LIU 等[16]提出了一种考虑MR 制动器迟滞现象的亚迟滞模型；YADMELLAT 等[17]提出了针对磁流变器件迟滞特性的自适应模型，采用多项式近似描述磁路(电流-磁场)的迟滞，采用Bingham 和Bouc-Wen 模型描述磁流变液(磁场-转矩)的迟滞，发现自适应模型比Preisach 模型能更加准确地解释迟滞现象。为了描述双向磁流变器件的迟滞效应，NGUYEN 等[18]提出了一种基于CBH 的一致性迟滞模型。其他学者也开发了一些非参数模型来表示磁流变离合器的迟滞行为。NAJMAEI 等[19]提出了一种人工神经网络模型来描述磁变流离合器输出转矩与磁场之间的非线性迟滞特性，并用试验证明了该模型的有效性。YU等[20]提出了一种基于支持向量回归(SVR)的磁流变弹性体隔离器的非参数化模型，发现训练后的模型可以很好地捕捉到隔振器的动态响应。然而，非参数模型的训练在数值上是密集且耗费时间，即使训练好了模型，仍然难以保证其鲁棒性和准确性。

建立基于磁流变器件模型的关键是简化现有模型，同时还能保持相似的建模精度。在参数识别过程中，通常同时识别所有模型参数，这可能会增加计算成本，导致计算时间增长。此外，有些参数本质上是冗余的，通过删除一些不必要的模型结构和参数，可以使数学模型能以更简单的描述接近更真实的物理现象。同时，模型中存在的非线性或不连续性的数学公式往往会增加模型参数辨识的难度。如果不能预先选取到良好的初始值，辨识参数时将难以获得全局最优解。

为此，首先，搭建磁流变离合器迟滞特性测试台，得到磁流变离合器转矩-电流迟滞曲线；其次，探讨和分析影响迟滞行为的因素，通过去除多余的描述黏性项与压力项的模型结构，提出一种简化的Bouc-Wen模型来诠释MR离合器的电流-转矩滞回行为；最后，针对Bouc-Wen 模型中的非线性和不连续性易导致模型参数辨识困难的问题，采用基于柯西变异的改进遗传算法对不同参数条件下的相关模型参数进行识别。

1 磁流变离合器的迟滞特性

1.1 磁流变离合器原型

磁流变离合器因其优异的性能而被广泛应用于转矩控制装置中，它通常以剪切模式工作，通过外部磁场实现驱动和从动部件的柔性连接。设计1 种双间隙单线圈的剪切式磁流变离合器结构，研究电流和转矩之间的迟滞行为，如图1所示。由图1可见：主动转子由左右驱动盘与隔磁环组成，并与驱动轴固定连接。隔磁环减少磁通在径向的漏磁，并使驱动盘和从动盘分离，构成一定厚度的工作间隙。右驱动盘与从动轴之间存在动密封，可以有效地防止磁流变液的泄漏。磁路由磁壳、驱动盘和从动盘构成磁流变液的磁通路径。通过在线圈中施加不同的电流强度，可以连续输出转矩。

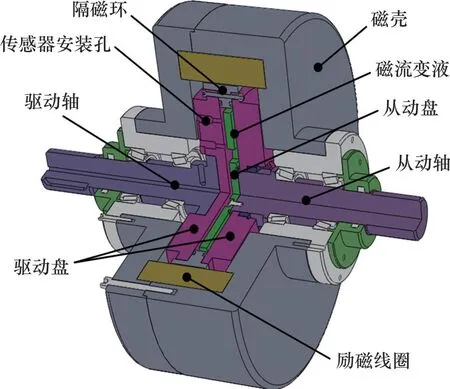
图1 磁流变离合器结构配置图Fig.1 Structure configuration diagram of MR clutch

1.2 磁流变离合器的非线性迟滞特性

为了研究磁流变离合器的迟滞特性，对原型进行探索性试验。

1)近似对称的迟滞回线。图2所示为迟滞特性曲线。由图2(a)可见：设定励磁电流在40 s 内由0 A 增大到1.6 A，然后再减小到0 A。试验发现磁流变离合器的电流-转矩曲线存在滞回现象，此外，迟滞回线表现出近似对称性，这便于采用参数化模型来捕捉这种行为。

2)迟滞行为来源。迟滞行为实际上是由构成磁路组成部分的铁磁材料和磁流变液本身的磁滞所引起的。图2(b)为试验测试的磁流变离合器铁磁材料的迟滞特性，图2(c)为试验测试的磁流变液的迟滞特性。虽然铁磁材料的磁滞特性比磁流变液强，但磁流变液本身也具有磁滞特性，而不是如AN等[13]所认为的近似线性的迟滞性能。减小磁滞损耗的可行方法是增大磁通路径长度与流经磁通截面积的比[21]，该比值与磁路的磁阻呈正比。

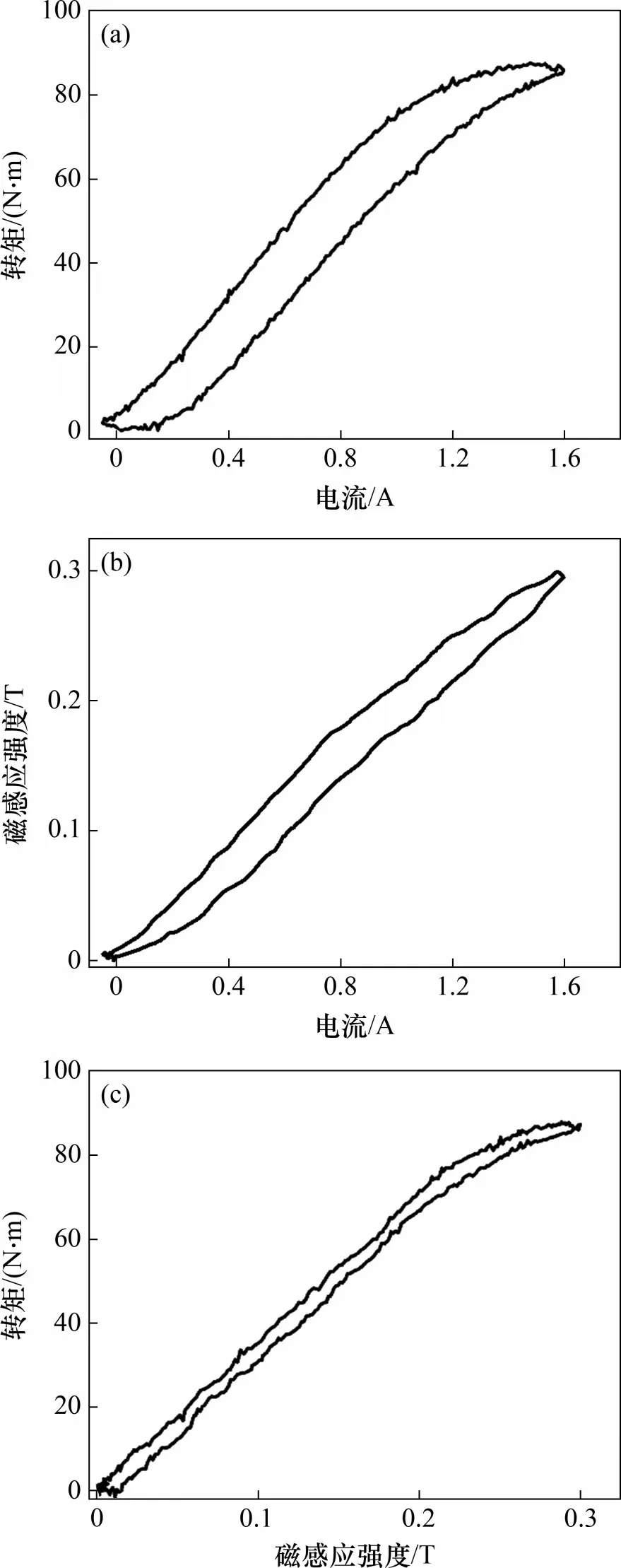
图2 磁流变离合器迟滞特性曲线Fig.2 Curve of hysteresis property of MR clutch

3)转速无关性。图3所示为转矩与转速之间的关系(未滤波处理)。由图3可见：励磁转速由300 r/min增大到1 500 r/min，然后减小到300 r/min。但从图3可见，MR 离合器转矩与转速之间没有明显的滞后，说明转速变化对转矩没有明显动态影响。这可能是因为磁流变离合器在磁流变液的预屈服区工作所导致的。

图3 转矩与转速之间的关系(未滤波处理)Fig.3 Curve of torque and rotational speed(without filtering)

4)频率相关性。图4(a)所示为不同电流频率下磁流变离合器动态转矩-电流特性的试验曲线。试验测试时，设定电流幅值为1.6 A，电流频率分别为0.005，0.020 和0.100 Hz，采用半周三角波信号进行3 组试验。由图4(a)可见：电流-转矩曲线在小频率处近似为线性，滞回回路较窄。频率越大，滞回线越宽，说明非线性特性越明显。滞回曲线的形状和位置随电流频率变化而变化，表明迟滞与电流频率具有相关性。

5)幅值相关性。图4(b)所示为不同电流幅值下磁流变离合器动态转矩-电流特性的试验曲线。试验测试时，设定电流频率为0.010 Hz，电流幅值分别为0.8，1.2 和1.6 A。由图4(b) 可见：励磁电流的幅值直接影响迟滞回线的形状和大小。迟滞回线的幅值随着电流幅值增大而增大。这说明磁流变离合器电流-转矩之间的滞回现象具有宏观的电流幅值相关性。这种非线性会对磁流变离合器的性能产生一定影响，如对控制系统带来跟踪误差和极限环等。

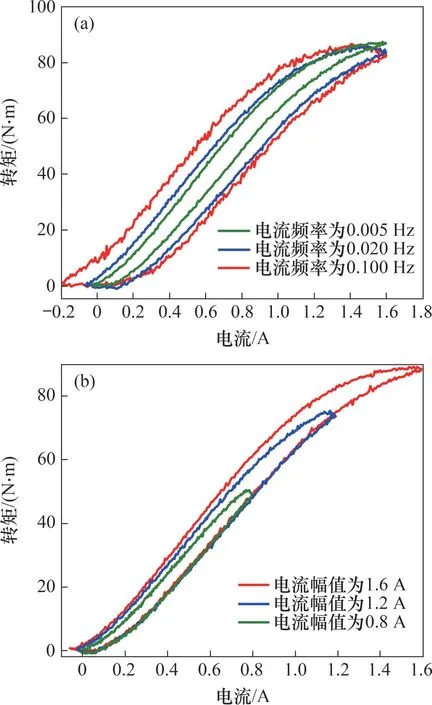
图4 转矩-电流迟滞特性Fig.4 Hysteresis characteristics of torque relative to current

2 迟滞建模与参数辨识

2.1 磁流变离合器的Bingham模型

一般来说，剪切模式下工作的磁流变离合器或制动器通常采用Bingham 或Herschel-Bulkley 模型。Bingham 模型是一种最简单、最常用的模型，其表现为在屈服前为刚体，在屈服后为牛顿流体。Bingham模型揭示了磁流变液的本构关系，被用于磁流变器件的结构几何设计和初步性能分析。Bingham模型如式(1)所示：

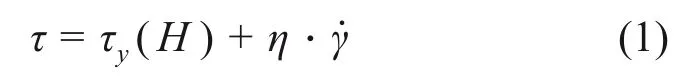
式中：τ为剪切屈服应力；τy(H)为磁致剪切应力，取决于磁场强度H；为剪切速率；η为流体黏度。

2.2 磁流变离合器的Bouc-Wen模型

Bouc-Wen(B-W)模型由Bouc 提出并由Wen 对其进行了改进[22]，其数学形式简单，能够表示迟滞行为，本质上是1个一阶非线性微分方程，它以1种滞后的方式将输入与输出联系起来。通过选择1组适当的参数，使模型的响应适应于真实的迟滞回线。

考虑T=[t0,t]∈R。状态量x(t)，z(t):T→R，矢量函数f:(Rm,Rm,R,R) →Rm和输入量u(t):T→R。其中：T为时间向量；t0为初始时间；t为时间变量；R为实数；m为阶次。

Bouc-Wen可以描述为

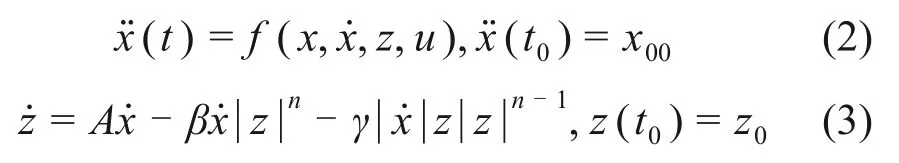
式中：x00和z分别为振子的位置和作用在振子上的滞回力；z0为振子在初始时刻的滞回力；A，β，γ和n分别为影响滞回线幅值、滞回线形状参数、过渡段线性度和平滑度。

将基于B-W 的唯象模型引入到磁流变阻尼器中来描述位移/速度与输出力的关系，该模型由阻尼器、弹簧和滞回系统并联组成[23]，如图5所示，其力学模型描述如下

图5 Bouc-Wen模型结构Fig.5 Bouc-Wen model structure

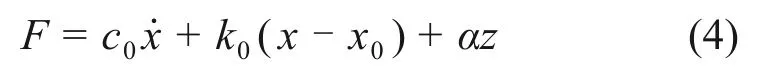
迟滞变量z为

式中：x和为阻尼器两端相对位移和相对速度；x0为弹簧的初始变形；F为阻尼力；c0为黏性常数；k0为弹簧刚度系数；α为滞回系数。

目前，磁流变离合器中尚未采用B-W 模型来描述电流与转矩之间的非线性关系。在描述磁流变阻尼器的原始模型中，位移作为自变量，阻尼力作为输出量。而在磁流变离合器模型中，电流作为自变量，转矩作为输出量。两者的运行原理与表现形式完全不同，原始的Bouc-Wen 模型已不再适用。为描述磁流变离合器中转矩与电流之间的非线性滞回，同时减少数学公式的复杂性，将B-W模型转换为：

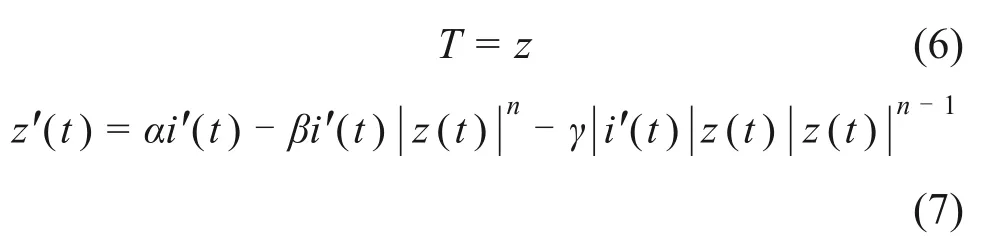
式中：z(t)为平滑滞回转矩；i(t)为励磁电流；T为输出转矩。

由式(6)和式(7)可以看出，相比原始B-W模型中存在7个参数，简化B-W模型只有4个参数。本文提出的简化B-W 模型以励磁电流为变量，可以预测不同励磁条件下的迟滞转矩。

2.3 模型参数辨识

B-W 模型的数学描述存在着非线性和不连续性，导致其参数辨识困难。此外，应用传统优化算法时易收敛于局部最小值，而不能求得全局最小值。遗传算法采用种群进化，在优化过程中不依赖于待解问题的复杂性，在个体种群初始化和基因重组过程中具有随机性。使用遗传算法进行曲线拟合时，只需要目标函数值[24-25]，就可以直接测量目标函数和变量。遗传算法的这种特性使其非常适合非连续性函数的优化，但如果不能选择到良好的参数初始值，遗传算法同样难以实现全局最优化。为此，本文提出1种基于柯西变换作为搜索算子的遗传算法，通过柯西分布积累函数对全部搜索的染色体变异，增加种群多样性，从而提高遗传算法的全局搜索能力。

采用遗传算法对参数进行识别时，一旦确定解的结构，就会产生相应可行性解的染色体。需要辨识的参数是α，β，γ和n。因此，染色体Φ变成

式中：N为测试点个数。

目标函数影响遗传进化，因此有必要确定目标函数。将模拟转矩和实测转矩之间的均方根误差定义为目标函数J，可以用式(9)表示：

式中：和Ti(t)分别为模拟转矩和试验转矩。

柯西分布在原点处峰值比较小，而在两端的分布比较长，其概率密度函数如式(10)所示。柯西变异可以在当前变异个体附近生成更大的扰动，使得柯西变异范围比较广，因此，采用柯西变异的两端分布更容易跳出局部极值。为充分利用柯西两端变异的特点，本文采用如式(10)所示的柯西逆累积分布函数。

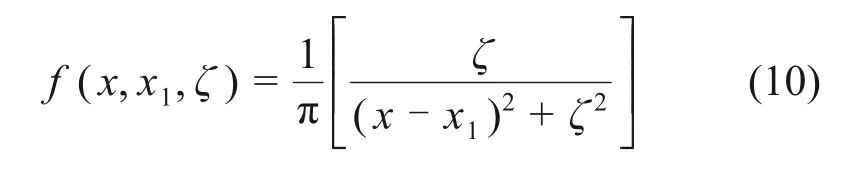
式中：x1为定义分布峰值位置的位置参数；ζ为最大值一半处的一半宽度的尺度参数。

当种群在进行全局搜索时，随机选择1个个体作为参考，其他个体随机靠近参考个体。在传统的遗传算法中，参考个体是随机选择的，不易寻到全局最优解。本文则以柯西逆累积分布函数[26]对个体进行变异，通过柯西分布有很长尾巴的特点，让个体朝着更广的范围变异。柯西逆累积分布函数F-1(p,x1,ζ)如式(11)所示。

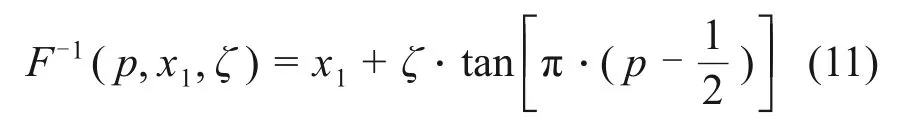
采用柯西变异的遗传算法流程图如图6所示。

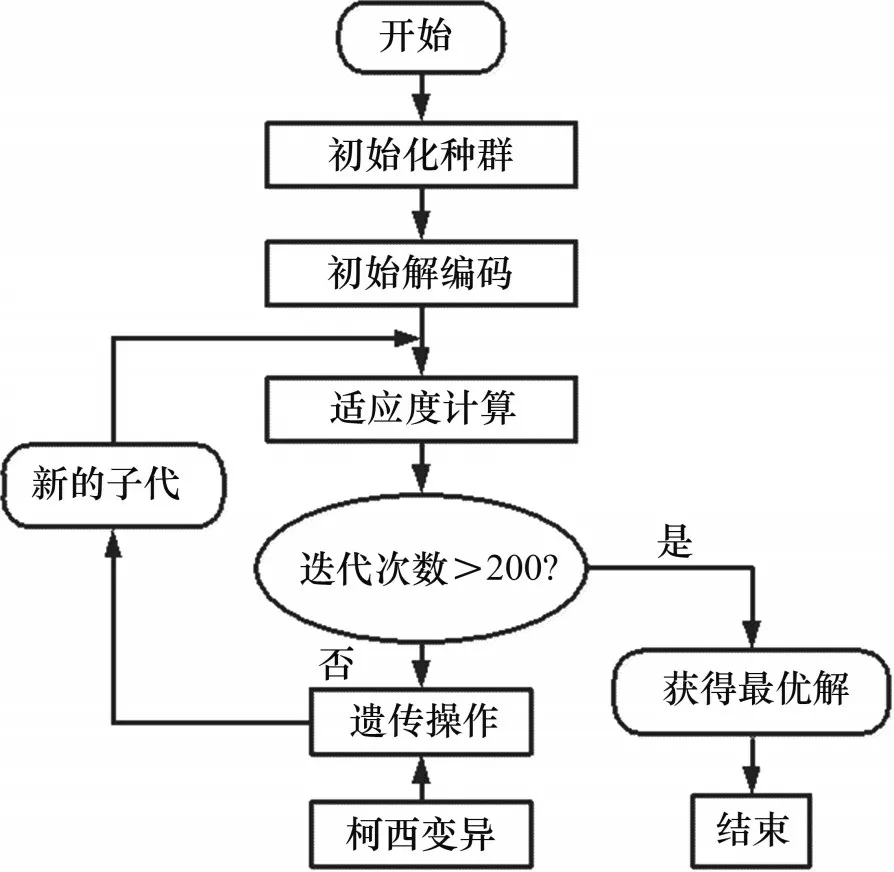
图6 基于柯西变异的遗传算法Fig.6 Genetic algorithm based on Cauchy mutation

系统辨识时，首先通过试验采集一系列试验数据点用于遗传算法辨识模型参数，随后将模型生成数据与实验测试数据进行对比，直到满足图6所示的迭代程序。参数辨识原理图如图7所示。为了识别模型参数，需要将指标最小化，使系统的模拟行为尽可能接近试验测试。

图7 磁流变离合器模型参数辨识原理图Fig.7 Schematic diagram of identification of model parameters for MR clutch

为了对比传统遗传算法与改进遗传算法对B-W模型的参数辨识能力，分别进行2种遗传算法(GA)下的参数辨识。表1所示为2 种GA 识别的B-W模型参数。

表1 2种GA识别的B-W模型参数Table 1 B-W model parameters identified by two kinds of GA

2.4 仿真与试验结果的对比

试验测试与2 种遗传算法辨识的B-W 模型模拟结果对比如图8所示。从图8可见：相比传统遗传算法，改进遗传算法辨识获得的B-W 模型更加贴合试验曲线，这说明：

图8 传统遗传算法与改进遗传算法下模型与试验对比曲线Fig.8 Comparison curves between model and test identified by traditional GA and improved GA

1)提出的简化B-W 模型能够准确地描述磁流变离合器转矩与电流之间的迟滞行为；

2)采用改进遗传算法识别的模型参数具有更高精度。

传统的遗传算法具有较窄的搜索域，容易陷入局部最优解而不能获得全局最优，初始解不同容易得到不同的最终解。而改进遗传算法通过柯西分布积累函数对全部搜索的染色体进行变异，增加种群多样性，从而提高遗传算法的全局搜索能力。此外，相比滞回线中间部分仿真曲线与试验曲线的差异，滞回线两端部分有较大差异。这是因为试验测试的迟滞特性并不是完全对称的迟滞回线形状，从而难以用B-W 模型在全局范围内对电流-转矩曲线进行一致地描述。

3 试验验证

3.1 MR离合器迟滞特性测试装置

为了评估简化的B-W 模型描述磁流变离合器电流-转矩迟滞特性的能力，建立基于磁流变离合器样机的试验系统，如图9所示。变频器用于调节电机，以改变磁流变离合器的输入速度。磁流变离合器的励磁电流由直流电源提供。采用磁粉制动器(MPB)加载离合输出轴，通过调节直流电源以调节负载转矩。采用转矩-转速传感器测量磁流变离合器输入轴、输出轴的转速和转矩，并将传感信号通过采集卡传输到LabVIEW 软件进行最终处理分析。

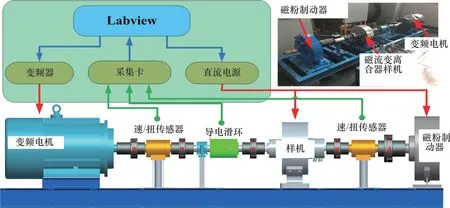
图9 磁流变离合器迟滞特性测试的试验装置Fig.9 Experimental setup for hysteresis tes of MR clutch

3.2 试验结果与分析

图10显示了在不同激励电流频率下，Bingham模型、提出的B-W 模型和试验测试在输出转矩及其误差随时间变化的对比。从图10可以看出，Bingham 模型与B-W 模型和试验测试结果在时域上都有较好一致性，这表明静态Bingham 模型和B-W模型都有预测磁流变离合器转矩输出的能力。但相比Bingham 模型，B-W 模型的转矩误差更小，尤其电流频率增加时，静态Bingham模型的转矩误差增大，精度降低，而动态B-W 模型始终可以跟随频率而保持较高精度。

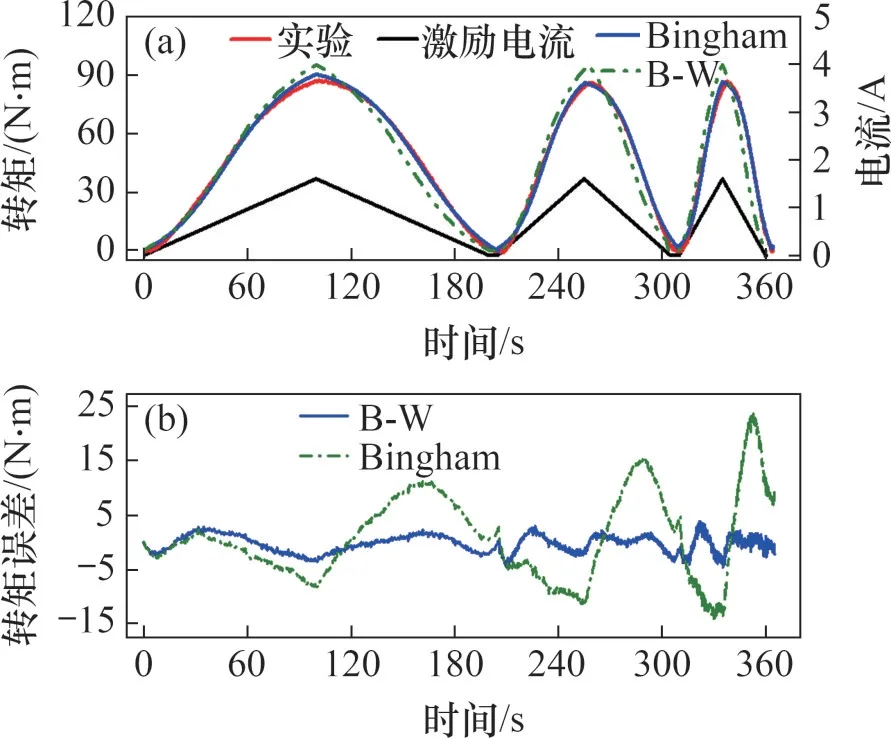
图10 不同激励电流频率下Bingham模型、B-W模型和试验测试的输出转矩与误差在时域上的结果对比Fig.10 Comparison between Bingham,B-W model and experimental tests in profiles of torque and error versus time at different excitation current frequencies

图11显示了在不同激励电流幅值下，Bingham模型、提出的B-W 模型和试验测试在输出转矩及其误差随时间变化的对比。从图11可见：不同激励电流幅值下，B-W 模型与Bingham 模型的输出曲线都能跟随试验曲线变化。但相比Bingham 模型，B-W模型的输出曲线更接近试验曲线。在3个励磁电流频率和3个励磁电流幅值下，B-W的下降沿转矩与试验测试之间的误差都比Bingham模型的小。这表明B-W 模型能较好地反映磁流变离合器输出转矩与励磁电流之间的迟滞行为，而静态Bingham模型只能用于静态设计和分析。

图11 不同激励电流幅值下Bingham模型、B-W模型和试验测试的输出转矩与误差在时域上的结果对比Fig.11 Comparison between the Bingham,B-W model and experimental tests in profiles of torque and error versus time at different excitation current amplitudes

表2和表3给出了按照式(9)计算的Bingham模型与B-W模型在不同电流频率与电流幅值激励下输出转矩的均方根误差。从表2可见：A=1.6 A，f分别为0.005，0.020 和0.100 Hz 时，3 种激励电流频率下Bingham 模型的均方根误差分别为5.27，8.40和12.42 N·m，而在相同情况下的B-W模型的均方根误差分别为1.63，1.60 和1.88 N·m。从表3可以看出：f=0.010 Hz，A分别为1.6，1.2 和0.8 A 这3种激励电流幅值下Bingham模型的均方根误差分别为6.58，5.16和4.05 N·m，而在相同情况下的B-W模型的均方根误差分别为1.83，0.74 和1.07 N·m，这同样说明了B-W模型具有更高精度。

表2 不同电流频率下2个模型的均方根误差(RSME)Table 2 Root-mean-square error between two models and tests at different current frequencies(RSME) N·m

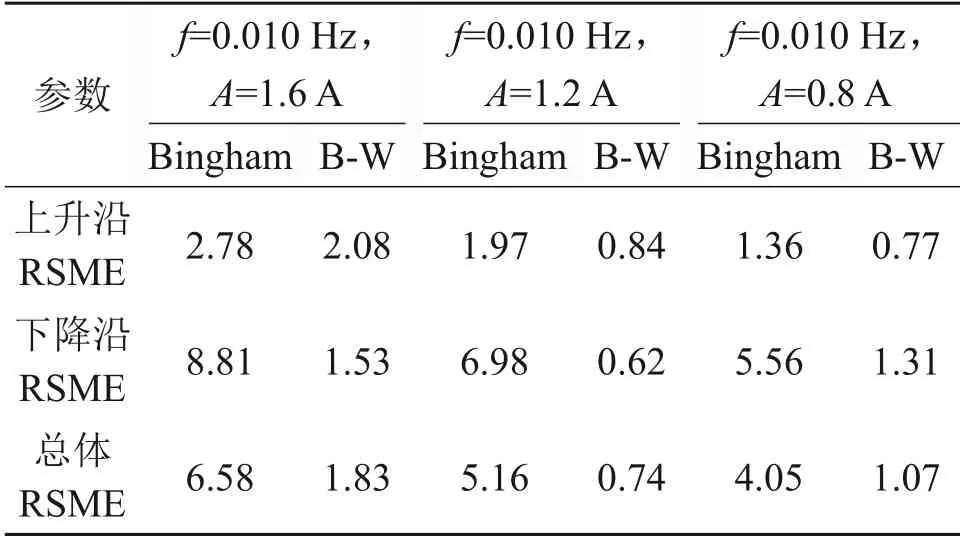
表3 不同电流幅值下2个模型及试验的均方根误差(RSME)Table 3 Root-mean-square error between two models and tests at different current amplitudes(RSME) N·m

4 结论

1)搭建磁流变离合器磁滞特性试验平台，试验发现磁流变离合器迟滞曲线具有近似对称性、转速无关性、电流幅值相关性和电流频率相关性。

2)提出一种简化的Bouc-Wen模型描述磁流变离合器的迟滞特性，该模型结构简单，参数较少，便于参数识别。相比静态Bingham 模型，简化的Bouc-Wen 模型能更精确地描述输入电流与输出转矩之间的迟滞关系。

3)提出一种基于柯西变异的遗传优化算法，该方法能够增加种群的多样性，有助于算法局部最优解的逃逸。相比传统遗传算法，改进的遗传算法在辨识Bouc-Wen 模型参数时具有更高的稳定性及寻求全局最优解的能力。