水产养殖机器鱼设计与三维路径跟踪控制

王懿偲，夏英凯，朱明，曾鑫，齐湘洪

华中农业大学工学院/农业农村部长江中下游农业装备重点实验室/农业农村部水产养殖设施工程重点实验室，武汉 430070

水下机器人作为水下工程装备中的一种，与传统水下作业模式相比，在作业环境与模式上均有着明显优势，对于提升水产养殖业的效率与品质有着重要意义[1]。仿生机器鱼作为水下机器人一种，相对于传统自治水下机器人（autonomous underwater vehicle，AUV）而言，其游动通过尾部摆动提供动力，具有更高的游动效率，同时仿生机器鱼游动时噪声小，最大程度上减小鱼群的应激反应，因此设计一款用于实时检测水质、监测鱼群状态的仿生机器鱼具有现实意义。为实现水产养殖作业精准化和智能化，机器鱼需要具有自主巡航与良好的路径跟踪控制能力。近年来，国内外学者针对仿生机器鱼路径跟踪控制方面开展了广泛的研究。宋晓茹等[2]基于自抗扰技术（active disturbance rejection control，ADRC）实现机器鱼路径跟踪控制。李宗刚等[3]基于中枢模式发生器（central pattern generator，CPG）与模糊控制相结合以实现机器鱼的定深控制。Yu等[4]基于滑模观测器（SMO）与视线制导律（line-of-sight，LOS）控制机器鱼运动，通过模糊控制调整机器鱼胸鳍攻角实现定深控制。Zou等[5]基于神经网络的离散滑模控制方法，实现多条仿生机器鱼协同轨迹跟踪任务。Castano等[6]基于平均动态模型，提出一种非线性模型预测控制方法使机器鱼在水平面内跟踪期望路径。需要指出的是，上述研究成果都局限在二维平面内，若想实现全水域监测，则需要机器鱼能有效地跟踪三维空间曲线，而三维空间曲线的路径跟踪相对二维平面其欠驱动的自由度增加2个，控制问题更加复杂。

针对三维路径跟踪控制问题，相关学者在常见的水下机器人方向已经开展了大量的研究。Wang等[7]通过反推法建立欠驱动AUV的运动学制导律，使AUV能够在外部扰动的情况下跟踪上期望路径。Wang等[8]通过Serret-Frenet坐标系以及LOS 法计算出所需偏航角，通过PID控制器对偏航角进行跟踪控制。Xu等[9]针对模型不确定性和外部干扰下欠驱动AUV路径跟踪问题，通过适当地选择积分器的控制增益，使AUV能较为精确地跟踪期望路径。李泽宇等[10]建立AUV路径跟踪导引律，基于RBF网络Q学习方法对滑模控制参数进行训练优化，提高AUV在不同航速及外扰动下的路径跟踪性能。然而，对于机器鱼而言，其主要依靠鱼尾摆动进行游动，相对于传统水下机器人而言，其模型更为复杂，机器鱼三维路径跟踪的研究成果相对较少。焦欧阳[11]针对机器鱼目标跟踪，利用反推控制使水下机器人跟踪期望目标点，但反推控制依赖精确的数学模型[12]，同时过高的控制增益会导致系统产生严重的抖振现象[13]。Suebsaiprom等[14]考虑到机器鱼在运动时类似于细长体AUV，基于李雅普诺夫稳定性理论与反步法的控制器，使机器鱼实现路径跟踪控制，但控制过程中容易产生抖振现象。Chen等[15]为方便深海网箱检查，设计了一种二关节仿生机器鱼，并基于模糊PID与CPG实现机器鱼的三维螺旋路径跟踪控制，但模糊PID较为依赖经验进行调参。

针对上述问题，本研究设计了一款水产养殖机器鱼，为监测水质与水下鱼群状态起辅助作用，该机器鱼搭载了水质传感器与网络摄像头，具备水质监测与观测鱼群状态的功能，并完成了机器鱼控制系统的设计。针对存在不确定扰动和模型不确定性情况下机器鱼的三维路径跟踪控制问题，本研究在Serret-Frenet坐标系下建立了机器鱼三维空间路径跟踪误差数学模型，基于LOS[16]与李雅普诺夫理论设计一种模糊滑模控制器，并对该控制算法进行对比仿真验证，旨在为机器鱼水下精准作业实际应用提供参考。

1 材料与方法

1.1 仿生机器鱼总体结构

水产养殖机器鱼主要由浸水舱、耐压舱、尾鳍摆动装置构成，其结构如图1所示，外壳使用尼龙材料通过3D打印技术成形，其总长约为1 000 mm，直径185 mm，质量约为13.1 kg，在水中为微正浮力状态。机器鱼的浸水舱与尾鳍完全浸入水中，搭载的摄像头、传感器和舵机都采用水密产品，其中位于艏部浸水舱中的水质传感器用于监测水质溶氧度、浊度与酸碱度参数，多普勒计程仪与深度传感器用于采集机器鱼位置信息，鱼鳍处安装WiFi模块与定位天线，并用密封胶将其密封，位于浸水舱中的水下舵机通过控制胸鳍摆动实现机器鱼上浮下潜。控制元器件位于耐压舱中，通过水密接插件实现与传感器、舵机之间数据传输，耐压舱两侧连接处装有密封圈以防止水进入舱内。安装在机器鱼尾部的2个水下舵机作为动力装置，输出不同的相位差可以实现机器鱼直线、转弯游动。

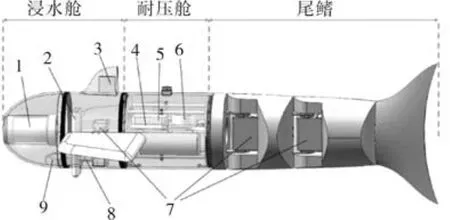
图1 水产养殖机器鱼三维结构图Fig.1 Three-dimensional structure diagram of aquaculture robotic fish

1.2 仿生机器鱼控制系统

为实现精准作业，本研究设计了如图2所示的仿生机器鱼控制系统硬件拓扑结构，该系统包括水上系统与水下系统。水下系统控制器采用树莓派，实现数据的整合与机器鱼的控制，当机器鱼位于水面游动时，UWB定位模块实时监测仿生机器鱼所处位置并通过通信系统将信息传输至水上系统。当机器鱼潜入水下游动时，UWB模块由于信号原因无法获取机器鱼位置信息，而水下机器人通常采用惯性导航系统获取位置信息，但由于其体积较大，不合适用于本研究的机器鱼中。因此，本研究导航系统通过多普勒计程仪[17]、深度传感器与陀螺仪采集机器鱼水下的游动速度与深度信息，并对速度积分可求出机器鱼位置信息。动力系统中采用2个水下舵机提供动力，位于浸水舱的水下舵机控制胸鳍角度调整。电源系统由24 V锂电池为系统各元件供电，并通过电压适配器为各元器件提供不同电压。感知系统用于收集水质信息与监测水下状态，并将搜集的水质信息传输至控制系统。通讯系统通过WiFi模块以及电力载波的形式实现信息的交互。上位机可实时显示当前水域水质信息以及水下环境，通过操纵按钮发出控制参数，控制鱼体运动。

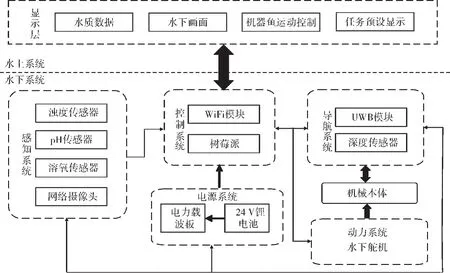
图2 水产养殖机器鱼控制系统结构框图Fig.2 Block diagram of the control system of aquaculture robotic fish

本研究基于ROS开发平台设计仿生机器鱼软件[18]，其系统结构如图3所示。仿生机器鱼软件由感知、通信、决策和控制等4层组成。在感知层中通过相关传感器收集机器鱼位置信息，滤波后将信息传输至控制层与通信层，在通信层中通过WiFi模块和电力载波实现与上位机的数据交换。在决策层中，将确定仿生机器鱼的工作模式，并将控制指令传输至控制层。执行仿生机器鱼的运动控制算法和驱动控制在控制层中实现。

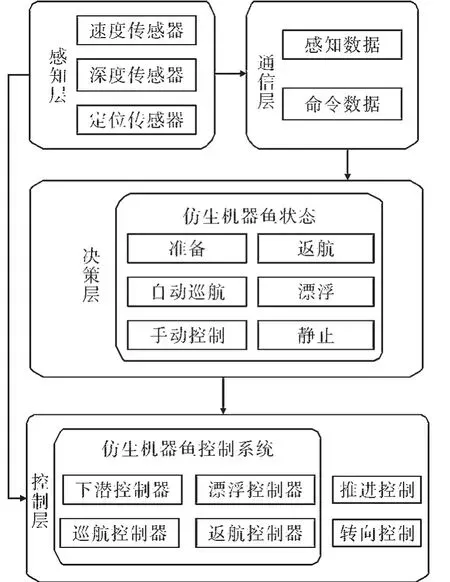
图3 水产养殖机器鱼软件系统结构框图Fig.3 The structure diagram of the aquaculture robotic fish software system

1.3 机器鱼数学模型

1）仿生机器鱼模型。为实现仿生机器鱼路径跟踪，基于Serret-Frenet坐标系建立路径跟踪误差方程，坐标系及参数定义如图4所示，其中：{I}、{B}和{SF}分别为惯性参考坐标系、载体坐标系和Serret-Frene坐标系。{B}坐标系的原点与仿生机器鱼质心重合，其xB轴指向机器鱼艏部方向，yB指向右舷，zB轴与xB轴和yB轴构成右手坐标系；{SF}坐标系的原点为期望路径上的任意一点P，其轴由切向量xSF、法向量ySF和副法向量zSF组成；s为P点的横坐标，c1(s)和c2(s)分别为路径的曲率和挠率。期望视线角(LOS)为ψlos、θlos；航向误差角为ψe、θe；Δy、Δz为视线距离。

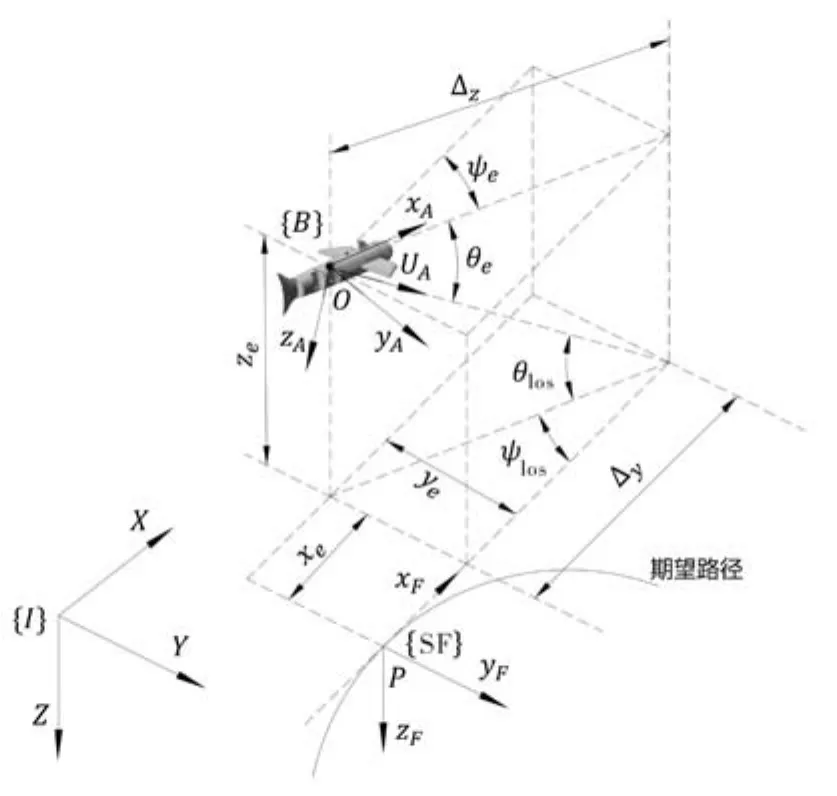
图4 空间路径跟踪控制坐标系Fig.4 Space path tracking control coordinate system

图4中，(x，y，z)为{I}坐标系下O点的坐标位置 ；(xe，ye，ze)为 {SF}坐 标 系 下P点 的 位 置 ；u、v、w、q和r分别为机器鱼在{B}坐标系下的纵向速度、横向速度、垂向速度、纵倾角速度及回转角速度；机器鱼的航向角与潜浮角分别为ψw=ψ+β，θw=θ+α； 其 中 ，分别为攻角与漂角；定义{SF}坐标系相对于{I}坐标系的姿态角为和，并 且 有。

本研究的仿生机器鱼质量均匀分布，且为零浮力，忽略高于2阶非线性水动力阻尼项，不考虑横摇运动的影响，因此，水下机器人的5自由度运动学模型[19]和动力学模型[20]如下：

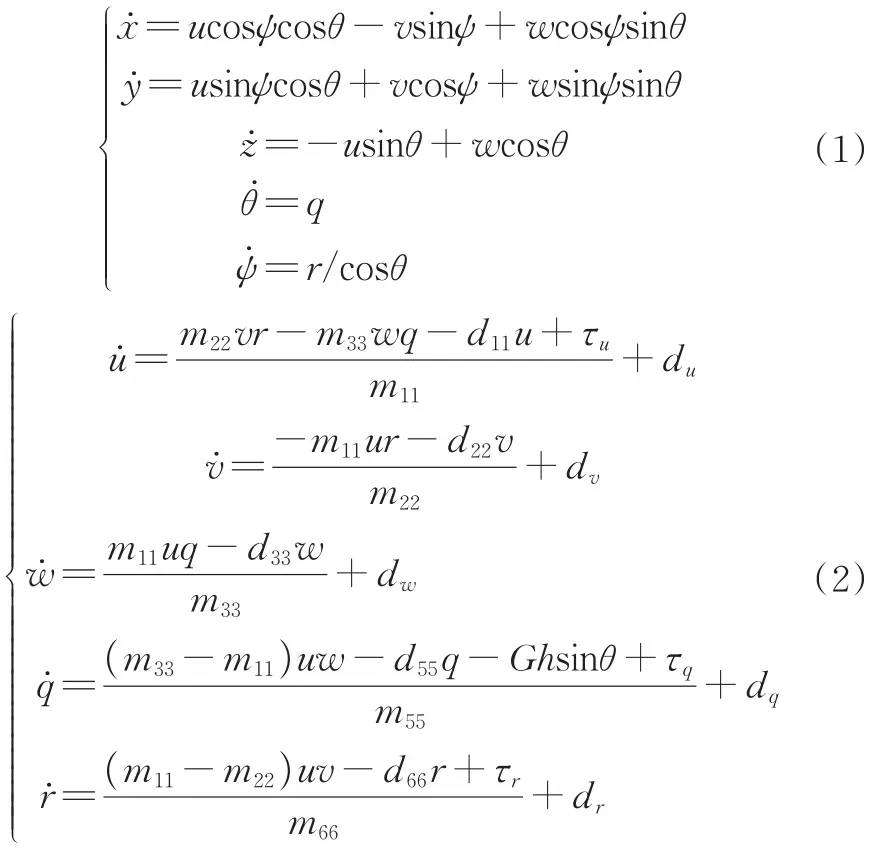
其中，mii(i=1，2，3，5，6)为机器鱼惯性质量和流体附加质量；dii(i=1，2，3，5，6)为机器鱼线性流体动力参数；dk，k=u，v，w，q，r分别为机器鱼在运动过程中受到的干扰；G为机器鱼的浮力；h为重心和浮心之间的垂向距离。τu为机器鱼沿xB轴方向控制输入的力，τq和τr为机器鱼绕yB轴与zB轴输入的力矩。

将式（2）中子系统u、q和r简化为：

在机器鱼载体中，潜浮控制力矩τq由胸鳍舵板产生，航速控制力矩τu和航向控制力矩τr由艉部的2个舵机耦合产生。在实际试验时，潜浮控制相对简单，可通过τq直接推算出胸鳍舵板的控制角度；进行航速和航向控制时，可先构建两输入-两输出的舵角-力矩模型，然后通过伪逆法或二次优化的方法解算出实际控制舵角的大小。本研究仅针对机器鱼的三维路径跟踪控制问题，进行控制方法和仿真研究，因此暂不讨论舵角与力矩之间的控制解算问题，在后续研究中将进一步介绍。

2）路径跟踪误差模型。将{I}坐标系下的机器鱼和期望路径上点P的位置误差转换至{SF}坐标系下，其误差方程[21]如下：

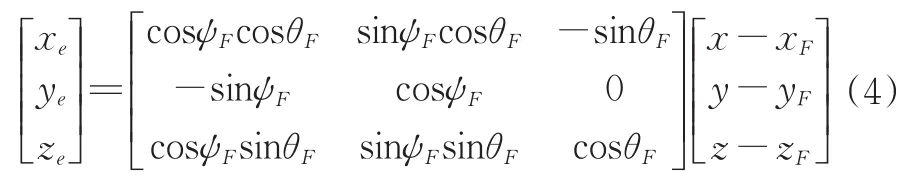
对（4）式求导得误差动力学方程[22]为：

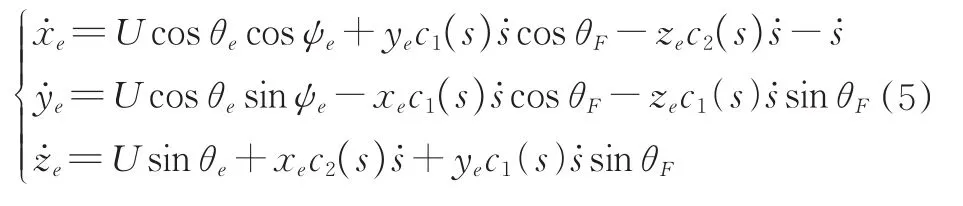
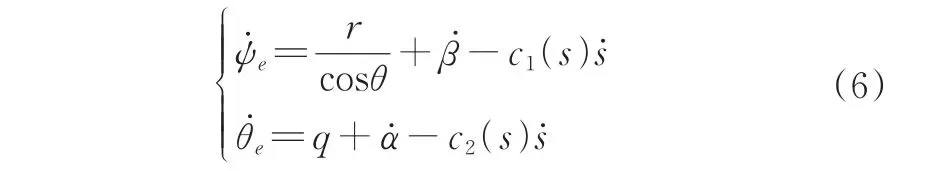
3）控制问题描述。本研究的目标是设计一款控制器使机器鱼在三维空间中跟踪期望路径，由于路径跟踪控制问题与时间无关，因此，假设机器鱼前向运动的速度ud为常数，基于机器鱼运动学模型，推导出有效的运动学控制律，以产生期望的纵倾角速度qd和回转角速度rd，使路径跟踪误差在t→∞时收敛到零。并建立有效的动力学控制律，以产生控制输入τu，τr和τq，使误差xe，ye，ze和u-ud在t→ ∞时收敛到零。

为方便机器鱼路径跟踪控制，作出以下假设：

假设1：机器鱼期望路径xd，yd和zd是有界的。

1.4 机器鱼路径跟踪控制器设计

图5为仿生机器鱼路径跟踪控制器结构图，控制器设计分为两步完成。第一步通过三维LOS制导法获得机器鱼期望角度，使虚拟目标沿期望路径运动，得到运动学控制器。第二步为解决外部环境不确定干扰，基于干扰观测器的模糊滑模控制来解决机器鱼动力学问题。

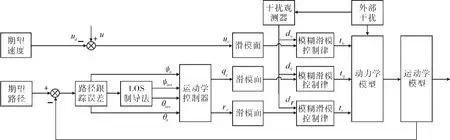
图5 机器鱼路径跟踪控制图Fig.5 Control block diagram of robot fish path tracking

1）位置控制率的设计。为了实现机器鱼制导与控制，利用以下LOS制导律[24]。

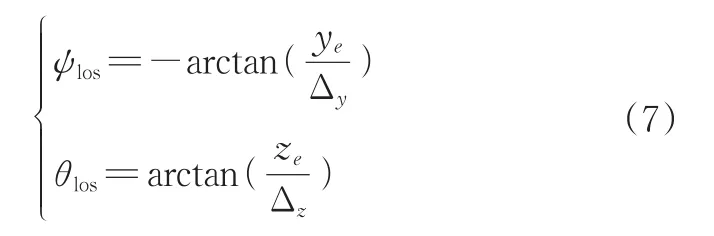
构造李雅普诺夫函数为：

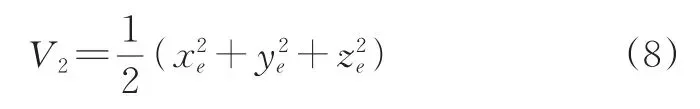
对公式（8）进行时间求导并带入公式（5）可得：

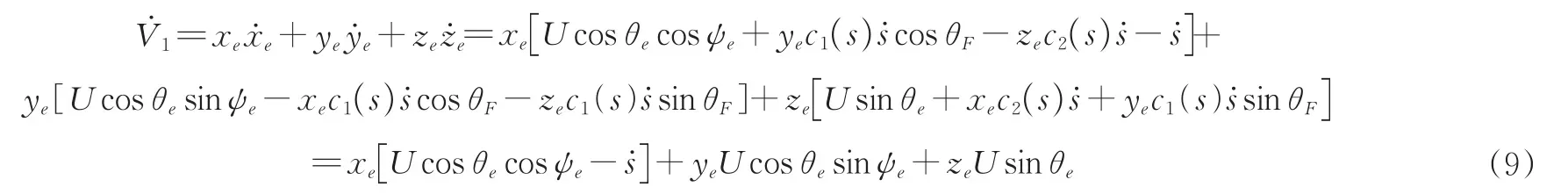
为使̇1＜0，设计虚拟向导速度控制律为：

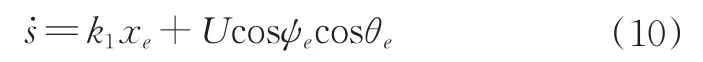
其中，k1＞0为设计的控制增益，并将公式（7）与（10）代入（9）中可得：

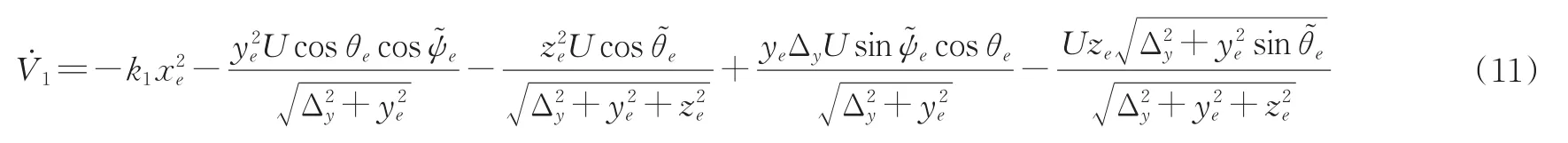
2）姿态子系统运动学控制率设计。为使机器鱼达到路径跟踪的目的，设计所需跟踪误差角[25]为：

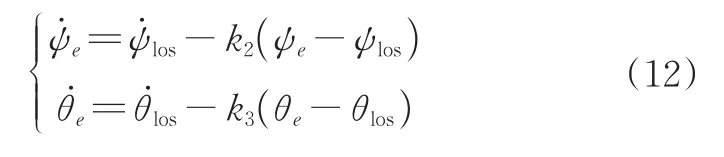
其中，k2＞0，k3＞0，为设计的控制增益，为得到期望回转角速度与纵倾角速度，将公式（12）带入（6）可得：

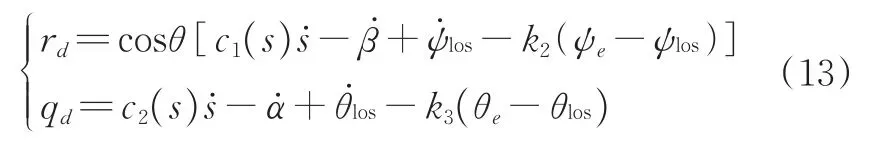
3）干扰观测器设计。为了估计未知环境的扰动，设计以下干扰观测器：

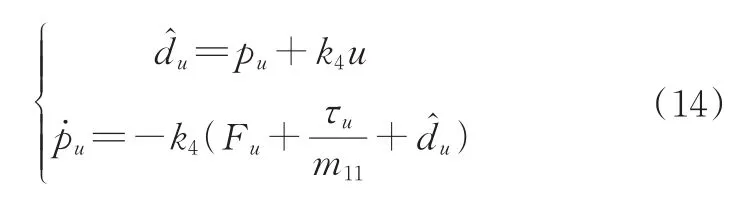
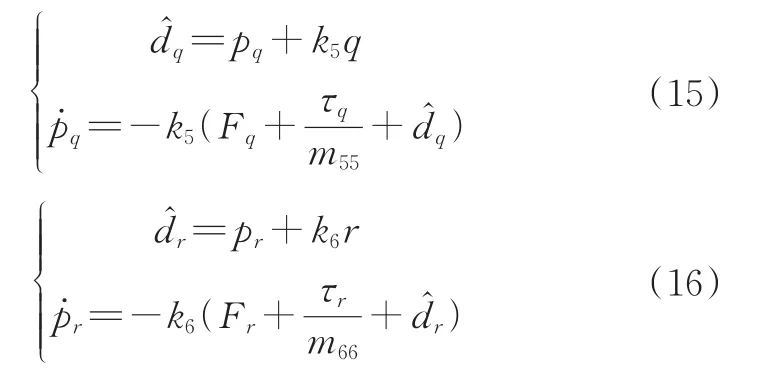
其中，pu、pq和pr为设计的辅助变量，k4、k5和k6为正数。

4）航速控制律设计。通过控制输入τu，当t→∞时，使机器鱼纵向速度u最终可以收敛到所需的期望航速ud，定义纵向速度跟踪误差为：

为实现纵向角速度的跟踪，采用滑模控制方法，并选择滑模面为：

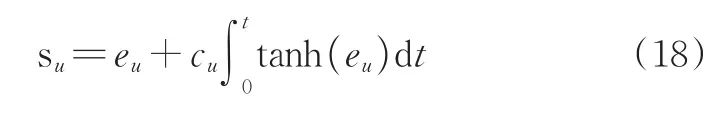
其中，cu＞0，对公式（18）求导可得：

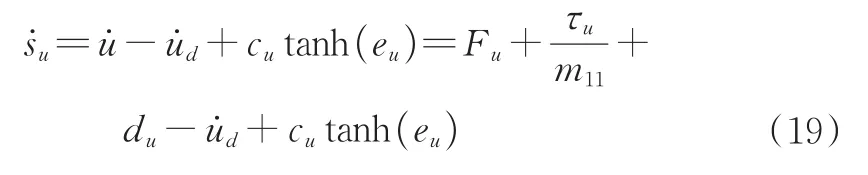
为提高系统收敛效率，采用以下趋近定律：

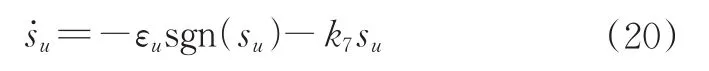
其中，εu＞0，k7＞0，将（20）带入（19），其纵倾角控制输入τu设计为：

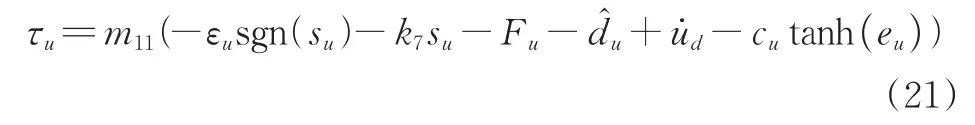
5）纵倾控制律设计。定义艏向角速度跟踪误差为：

与本文“1.3 4）”类似，设计滑模面为：

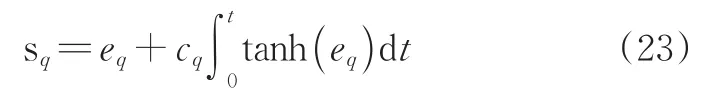
其中，cq＞0。纵倾角控制输入τq设计为：

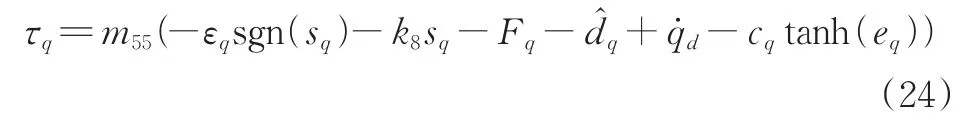
其中，εq＞0，k8＞0。

6）艏向控制律设计。定义艏向角速度跟踪误差为：

并选择滑模面为：

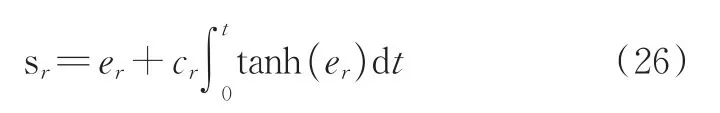
其中，cr＞0。艏向角控制输入τr设计为：

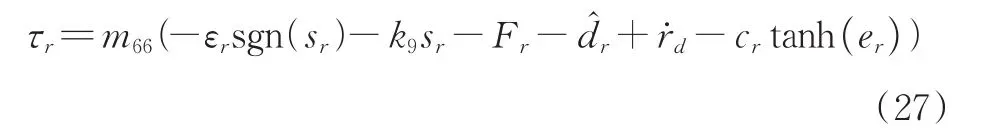
其中，εr＞0，k9＞0。

7）稳定性证明。选取如下李雅普诺夫函数：

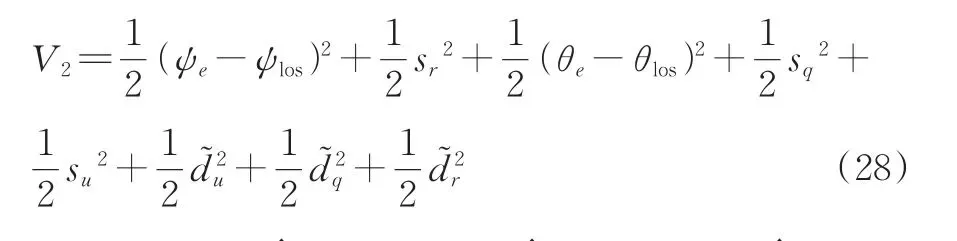
8）模糊滑模控制器设计。根据式（30）可以看出，V̇2收敛至零时，其收敛速度取决于k7、k8和k9，在指数趋近中，趋近速度从较大值逐步减小至零，使运动点到达切换面时的速度很小，当运动点接近滑模面s=0时，有ṡ=±ε，即运动点到达滑模面时的趋近速度是ε而不是零，可以保证运动点有限时间到达。当ε较大时，运动点穿过滑模面距离变大，引起系统剧烈抖振，但选取ε值较小时，虽然减小了抖振，但延长了系统的趋近时间。为保障系统能快速趋近的同时削弱抖振，应当在增大k的同时减小ε[26]。

综合上述情况，本研究滑模趋近律被重新设计为：

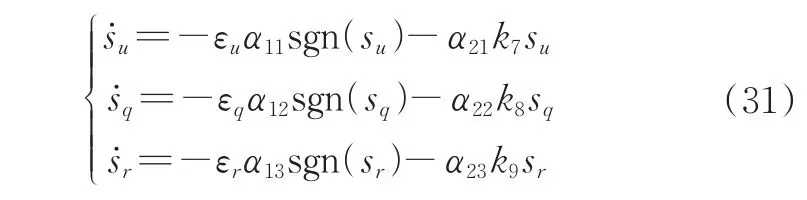
式（31）中，α1j、α2j（j=1，2，3）分别为模糊控制的输出值，选取运动点与滑模面之间的距离sl（l=u，q，r）为模糊控制的输入值，在本研究中，艏向、纵倾与航速的趋近律设计相同，因此，都采用一种模糊规则进行控制。如图5所示，系统的输入与输出的模糊量均用ZO（零）、PS（正小）、PM（正中）、PB（正大）为模糊子集，隶属度函数均采用三角形隶属度函数，并提出4条模糊规则：R1：if|sl|is ZO thenα1jis ZO，α2jis PM；R2：if|sl|is PS thenα1jis PS，α2jis PB；R3：if|sl|is PM thenα1jis PM，α2jis PS；R4：if|sl|is PB thenα1jis PB，α2jis ZO。

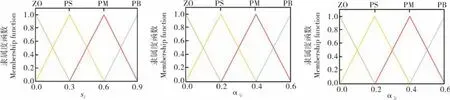
图6 模糊系统的隶属度函数Fig.6 Membership function of fuzzy systems

2 结果与分析

2.1 无干扰仿真对比

为验证所提出控制算法的有效性，利用Matlab软件对机器鱼控制系统进行仿真分析，并与常规PID、滑模控制器性能进行对比。仿生机器鱼各参数选取为：m11=25 kg，m22=17 kg，m33=30 kg，m55=22.5 kg，m66=15 kg，d11=30，d22=30，d33=30，d55=20，d66=20，Gh=5。选择期望路径为Pd(μ)=[μ，20cos(0.05μ)，20sin(0.05μ)]T；选择期望游速为ud=1 m/s；机器鱼初始状态为 ：η0=[0，10，0，0，0，0]T；初始速度为v0=[0.1，0，0，0.1，0.1]T；仿真选用普通工控机，CPU型号为Intel Core I5，仿真步长为0.01 s，仿真时间长度为100 s，计算方式选用ode3。控制器其他相关参数选择为：k1=0.1，k2=1，k3=20，k4=k5=k6=2.5，k7=20，k8=k9=1，εu=15，εq=εr=2，cu=cq=cr=1.5。其仿真结果如图7所示。

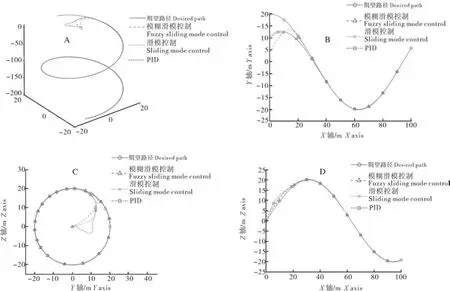
图7 机器鱼期望路径和实际路径Fig.7 Robot fish expected path and actual path

从图7可知，机器鱼通过模糊滑模控制跟踪至期望路径时间为38.7 s，滑模控制跟踪至期望路径时间为69.5 s，常规PID跟踪至期望路径时间为77.5 s。从图8可知，所提出的模糊滑模控制相对于常规PID与滑模控制，其收敛速度更快，超调量更小。从图9可知，模糊滑模控制相对于常规滑模明显减小了系统抖振，取得更好的控制效果。从图10可知，滑模控制器相对于常规PID与滑模控制器，输入力与力矩波动更小。

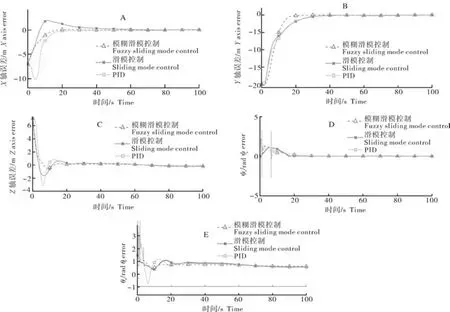
图8 机器鱼与期望轨迹直接的位置误差Fig.8 The position error between the robot fish and the expected trajectory

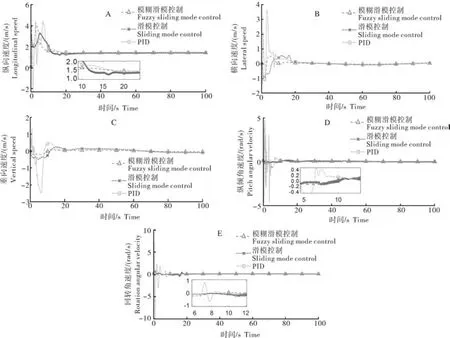
图9 机器鱼线速度和角速度Fig.9 Line speed and angular velocity of robotic fishing

图10 机器鱼控制输入力和输入力矩Fig.10 Robot fish controls input force and input torque

2.2 对干扰的鲁棒性能测试

本研究所设计的机器鱼主要在养殖水塘中作业，受到的水流较小，在机器鱼游动过程中，主要面对来自自身运动，如艏摇等方面的干扰。因此，为进一步验证所提出的控制器对干扰的鲁棒性能，进行了2种不同情况下扰动的仿真试验，并与无扰动系统进行对比，在干扰1中，机器鱼受到持续扰动，在干扰2中，机器鱼受到的扰动与时间相关。

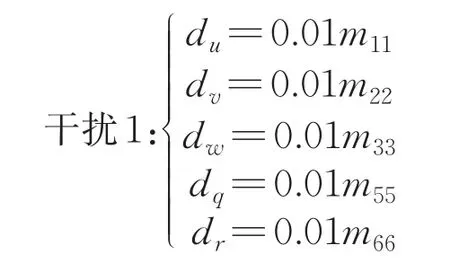
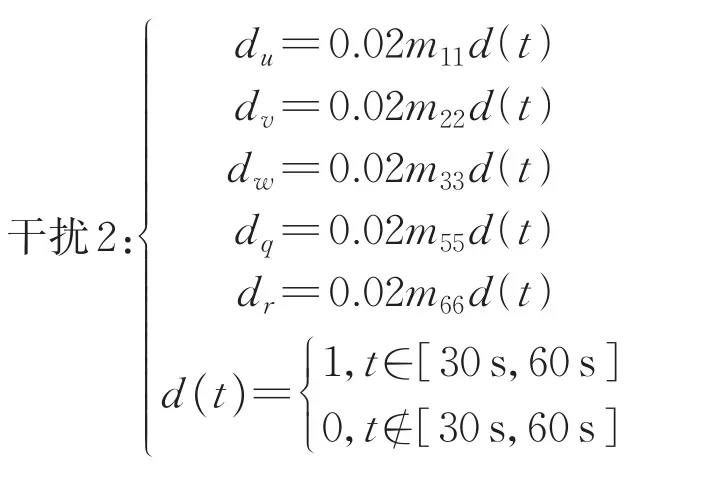
从图11可知，在加入扰动下，系统出现了一些波动，但仍然较为精确地跟踪期望路径，由此证明所研究的干扰观测器有效，三维路径跟踪算法在面对未知干扰时仍具备良好的精度及鲁棒性，上述特质为算法移植到真实样机提供了良好的条件。当然，必须指出，在面临真实环境中的复杂扰动时，相关控制参数需进一步优化。

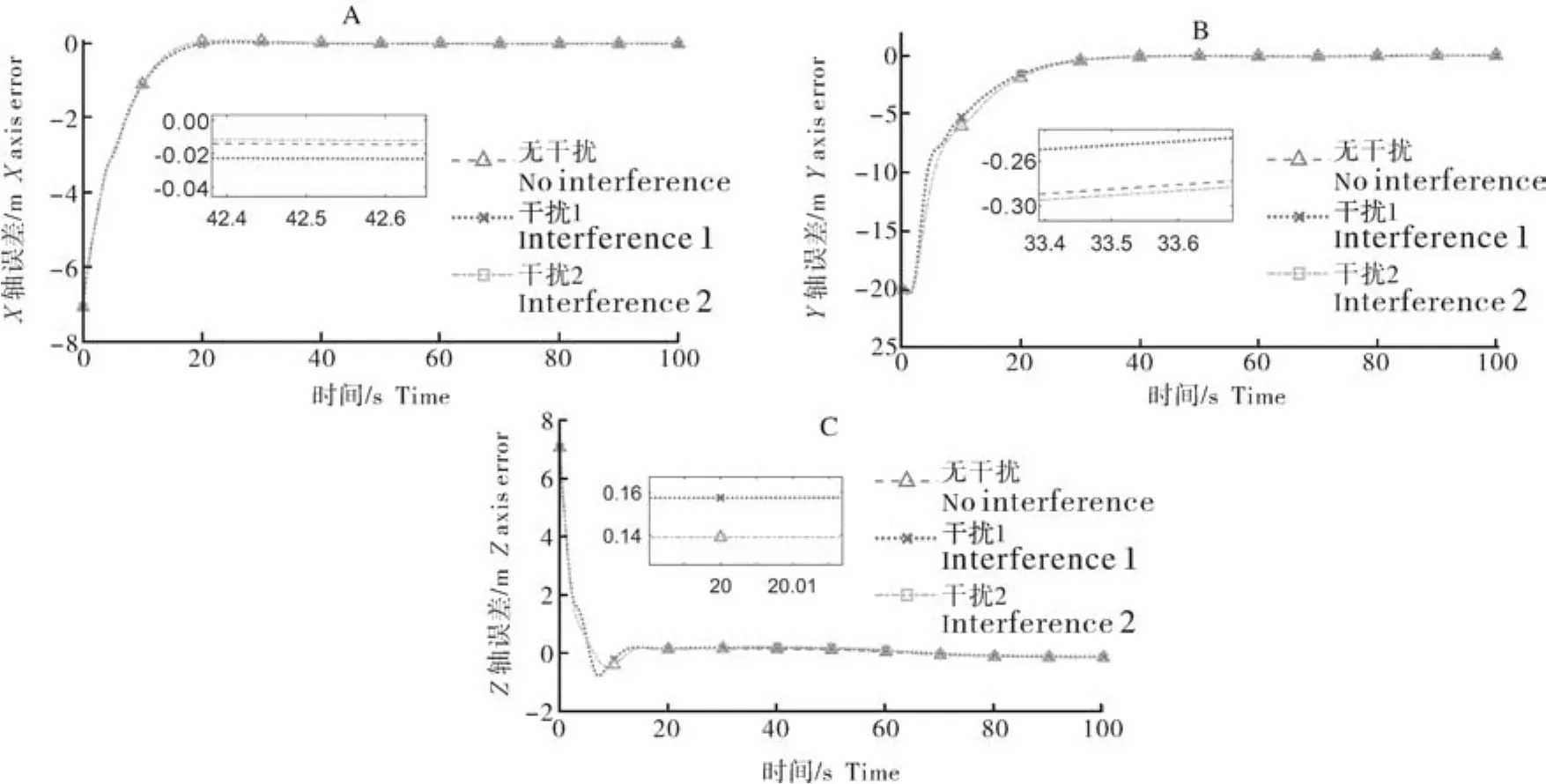
图11 不同扰动下的跟踪误差Fig.11 Tracking errors under different disturbances

3 讨论

本研究基于现代化水产养殖需求，设计了一款水产养殖机器鱼以实现全水域实时监测，通过软件系统可获得水域环境信息并对机器鱼进行控制，为水产养殖水质与水下环境监测起辅助作用。针对机器鱼三维路径跟踪控制问题，本研究通过Serret-Frenet坐标系下建立了机器鱼三维空间路径跟踪误差模型，由于难以精确建立机器鱼数学模型，因此在参数不确定的情况下，基于LOS制导法和李雅普诺夫理论设计一种模糊滑模控制器，通过Matlab对所提控制器与常规PID和滑模控制器进行对比。仿真结果验证模糊滑模控制器能够实现欠驱动机器鱼在模型参数不确定性下的三维路径跟踪控制，并且控制精度与鲁棒性明显优于常规PID与滑模控制器。限于论文篇幅及机器鱼加工进度等问题，本研究仅开展了数字仿真工作，证实了本文提出的算法具有良好的控制精度和鲁棒性，具备移植到实际样机中的条件，但考虑到实际试验环境中干扰会更加复杂，在进行样机试验时，还需进一步优化算法，相关内容将在后续研究中介绍。