模拟计算平行样对流域生物信息流估算的影响

杨海乐,张 辉,吴金明,李君轶,王成友,杜 浩,危起伟

中国水产科学研究院长江水产研究所,农业农村部淡水生物多样性保护重点实验室, 武汉 430223

流域生态学(watershed ecology)是研究流域范围内陆地和水体生态系统相互关系的学科(全国科学技术名词审定委员会),其主体在于整合研究以流域生态系统过程为核心所关联起的流域内各相关子系统(subsystem)[1]。流域生态系统过程研究的核心工作是研究流域生态系统中依托于水循环过程的各个子系统之间及之内的物质流、能量流、信息流[2]。流域生物信息流(watershed biological information flow)是生物信息依托于流域生态系统过程在不同空间和系统之间进行传递、交流、作用、反馈的路径、过程与控制,主要关注生物体及生物质所承载的生物信息在时空上的迁移扩散,以及与生物体及生物质间相互作用相伴随的生物信息作用和反馈[3]。任何生物能都依托于生物物质,而任何类型的生物物质都携带有其特定的信息标记,因而作为流域生态系统过程研究的三大主题(物质流、能量流、信息流)之一,流域生物信息流通过物质流、能量流、信息流的三位一体而具有对流域生态系统中的物质输移和能量输移过程的指征和标记功能,流域生物信息流的研究可以为流域生态系统研究中生物物质输移和生物能输移过程的跟踪和标记提供理论的可能和技术的支撑[4—5]。

河流上游到下游的流域生物信息流是eDNA(environmental DNA)技术调查评估河流水体中物种组成空间特征的事实基础[5—8],估算河流上游到下游的流域生物信息流是用eDNA技术调查评估河流水体中物种组成空间特征的方法基础[9—11]。基于集合生态系统概念框架,根据研究尺度和分辨率的需要,可以将流域生态系统构建为一个包含了多个子系统的集合生态系统(meta-ecosystem)[12]。评估河流水体中物种组成的空间特征,即评估河流水体(基于空间划分)各子系统中的物种组成。假设各子系统在特定时间的物种组成相对稳定,各子系统中的个体释放到环境中的eDNA则随着河川径流向下游输移。因为流水水体中的eDNA受释放、稀释、吸附、再悬浮、输移、降解等过程的影响[13—15],上游水体子系统中个体释放到环境中的eDNA随着河川径流向下输移的距离有限[16—18],因而可以通过估算流域生物信息流来评估河流水体各子系统中的物种组成,进而评估河流水体中物种组成的空间特征。

分析流域生物信息流,第一步是估算上游子系统到下游子系统的流域生物信息流输移有效度(即用下游样点水体eDNA监测上游样点水体中生物组成信息的监测有效度,上游样点水体中的水生生物信息能在下游样点水体的eDNA中被检出的比例和概率)[3]。监测有效度估算的核心是(1)有限采样对采样区域的生物组成信息的检出度和(2)由上游到下游的流域生物信息流输移有效度。在实践应用中,调查采样往往是有限的,因而存在两个问题：(1)平行样的设置情况如何影响生物组成信息检出度的估算,(2)平行样的设置情况如何影响流域生物信息流输移有效度的估算。基于抽样调查的基本原理和前期eDNA调查研究可知,采样数量越多对采样区域的生物组成信息的检出度越大,因检出度受多种因素影响,具体的平行样数量和检出度之间的关系需要一系列具体研究来进行量化[19]。如果将由上游到下游的流域生物信息流过程简化为上游区域生物信息通过随机取样然后转移到下游区域,那么基于有限采样的流域生物信息流估算就是对随机抽样调查结果的随机抽样调查,基于随机抽样调查的基本原理可以猜测,采样数量不影响抽样调查结果的准确度,但会影响其精密度。

根据流域生物信息流研究框架[3],本文就平行样的设置对流域生物信息流估算的影响展开了模拟计算,以检验“在流域生物信息流估算中各样点平行样数量不影响抽样调查结果的准确度,但会影响其精密度”的假设,并探讨在流域生物信息流估算中各样点平行样数量(检出度)的增加或减少对流域生物信息流估算的具体影响,为以下游水体eDNA监测上游水体中物种组成信息的监测有效度评估方案提供指导和支持,推动eDNA技术在水生生物多样性调查监测中的应用和发展。

1 研究方法

1.1 基本假设

随机抽样过程中,抽样数量越多,抽样结果的集合对整个系统的反映程度越全面。在本研究中,抽样即eDNA采样,抽样数量即eDNA样本数,对整个系统的反映程度即eDNA对该样点水体生物信息种类的检出度。因此在模拟计算中,我们将平行样数量的增加转化为对该样点水体生物信息种类检出度的增加。

上下游样点间共有生物信息种类组成占上游样点总生物信息种类组成的比例,即上游到下游的流域生物信息流。因为上下游相邻样点间的流域生物信息流是整体流域生物信息流计算的基础单元,所以本模拟计算中流域生物信息流的估算用上下游相邻样点间的共有生物信息组成占上游样点总生物信息组成的比例估算简单指代。

1.2 条件设定

平行样数量的增加对流域生物信息流估算的影响,用生物信息检出度的增加对上下游样点间共有生物信息种类组成占上游样点总生物信息种类组成的比例估算的影响来等价模拟展示。在本模拟计算中,设定上下游样点分别有生物信息1000种、900种(可颠倒替换),样点生物信息检出度和实际流域生物信息流作为两个自变量,估算流域生物信息流为因变量,进行单变量模拟,具体分组及参数如表1,然后计算特定上下游样点生物信息种类数组合情况下,样点生物信息检出度变化对估算流域生物信息流的影响(即实际流域生物信息流与估算流域生物信息流的差异)以及不同实际流域生物信息流条件下估算流域生物信息流的结果偏差程度。

1.3 计算方法

模拟计算的基本思路是,在特定上下游样点生物信息种类数组合情况下、在特定样点生物信息检出度情况下、在特定实际流域生物信息流情况下,通过随机取样计算得出某流域生物信息流值的概率,然后通过统计展示估算流域生物信息流相对于实际流域生物信息流的偏差,进而评估样点生物信息检出度变化对估算流域生物信息流的影响以及不同实际流域生物信息流条件下估算流域生物信息流的结果偏差程度。具体模拟计算公式如下列公式组

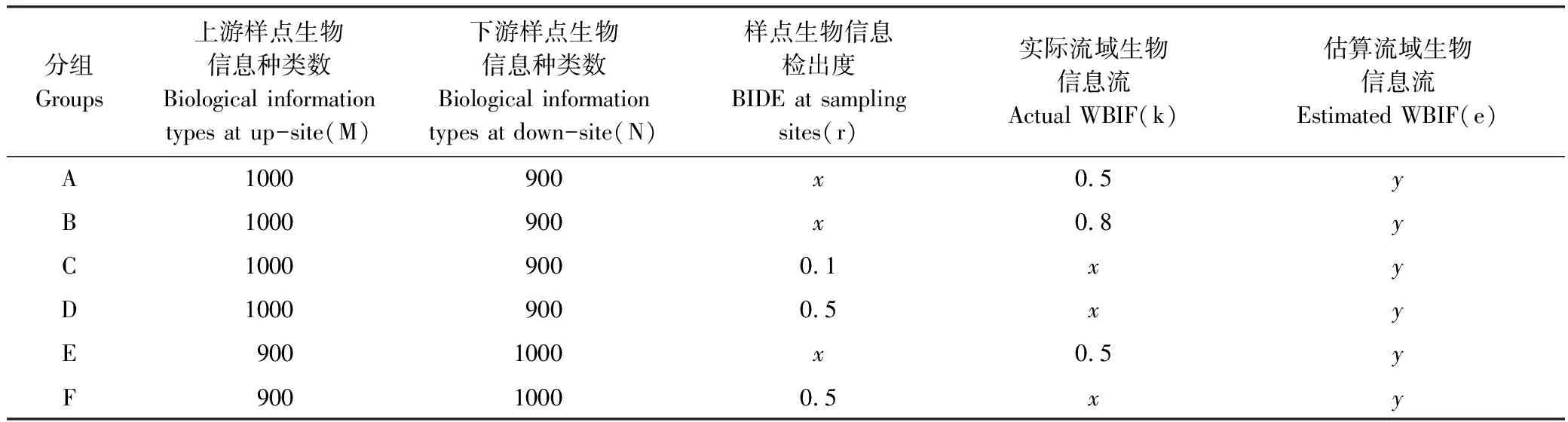
表1 不同样点生物信息检出度条件下的流域生物信息流估算条件分组及参数设置

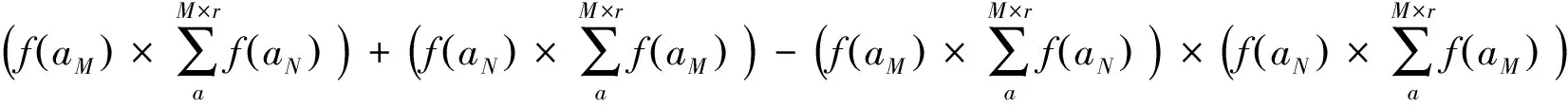
式中,M,上游样点生物信息种类数；N,下游样点生物信息种类数；r,样点生物信息检出度；k,实际流域生物信息流；a,监测到的生物信息种类数；y,所估算的流域生物信息流值；f(aM),上游样点处监测到数量为a的生物信息种类数的概率；f(aN),下游样点处监测到数量为a的生物信息种类数的概率；f(y),估算出流域生物信息流值为y的概率。

根据该公式组,按照上述参数设定分6组进行模拟计算,然后通过组内和组间模拟计算结果的对比分析,探讨(1)样点生物信息检出度状况对流域生物信息流估算的影响(即实际流域生物信息流与估算流域生物信息流的差异),(2)在特定样点生物信息检出度条件下,不同实际流域生物信息流状况对流域生物信息流估算的影响,(3)在特定样点生物信息检出度和实际流域生物信息流条件下,上下游样点生物信息种类数相对关系对流域生物信息流估算的影响。

2 结果与分析

2.1 样点生物信息检出度状况对估算流域生物信息流的影响

模拟计算显示,上下游样点分别有生物信息1000种、900种的条件下,在实际流域生物信息流水平在0.5的时候,(1)随着样点生物信息检出度从0.1逐步增长到0.9,估算流域生物信息流的最优估值从0.48(偏离4%)逐步增长到0.4978(偏离0.44%),即随着样点生物信息检出度的增长估算流域生物信息流的最优估值逐渐趋近于实际流域生物信息流水平；(2)随着样点生物信息检出度从0.1逐步增长到0.9,估算流域生物信息流的99.9%置信区间逐渐从0.34—0.59(最大偏离32%)收缩到0.4822—0.51(最大偏离3.56%),即随着样点生物信息检出度的增长估算流域生物信息流的估值区间逐渐集中于实际流域生物信息流水平(图1)。

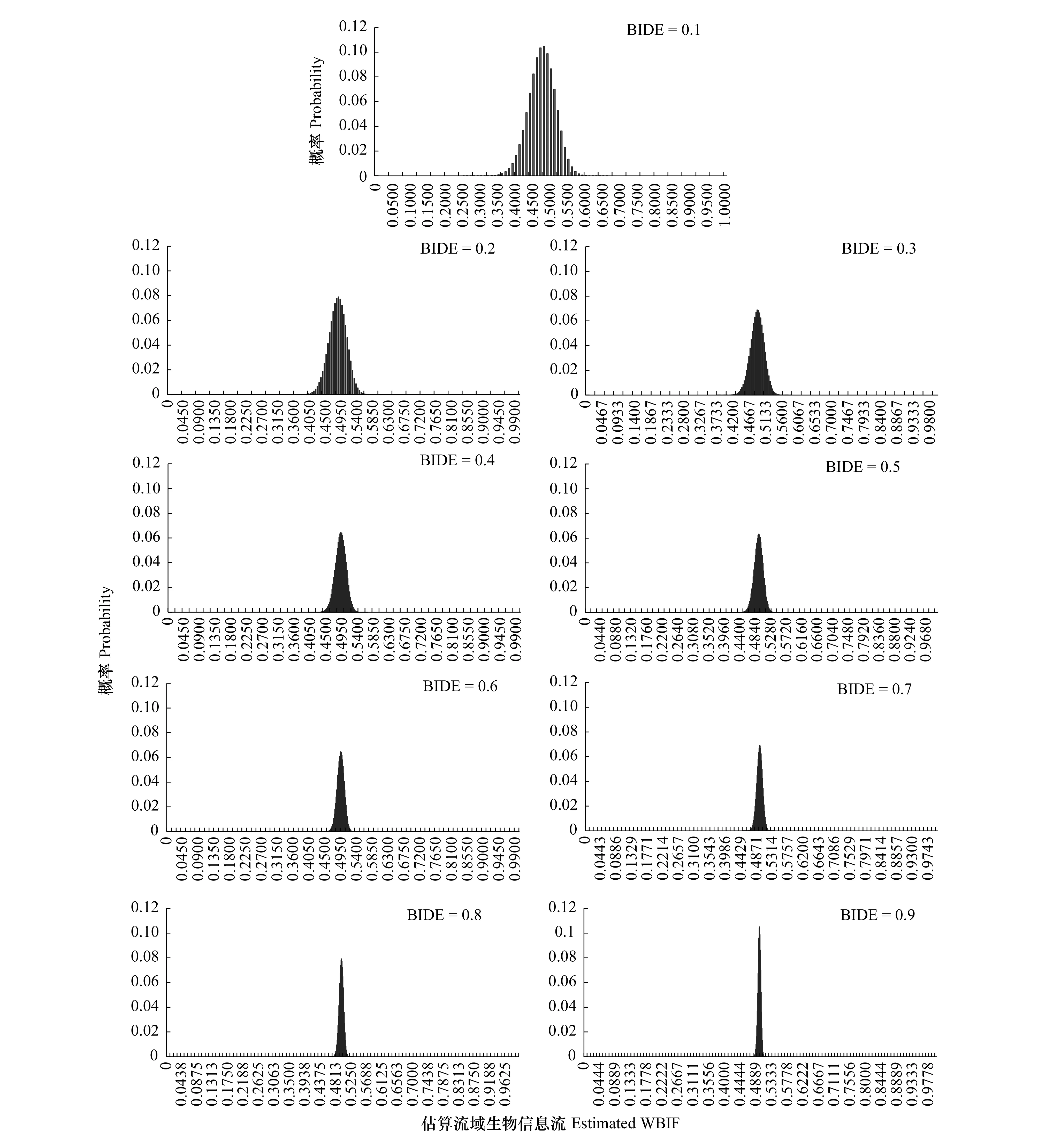
图1 不同样点生物信息检出度下(A组)估算流域生物信息流值的概率分布Fig.1 Probability distributions of estimated watershed biological information flow (WBIF) in different biological information detection efficiency (BIDE) conditions at sampling sites (group A)A组,上下游样点分别有生物信息1000种、900种,实际信息流水平为0.5,样点生物信息检出度为变量。WBIF：流域生物信息流 watershed biological information flow；BIDE：生物信息检出度 biological information detection efficiency

在实际流域生物信息流水平在0.8的时候,(1)随着样点生物信息检出度从0.1逐步增长到0.9,估算流域生物信息流的最优估值从0.79(偏离1.25%)逐步增长到0.7978(偏离0.275%),即随着样点生物信息检出度的增长估算流域生物信息流的最优估值逐渐趋近于实际流域生物信息流水平；(2)随着样点生物信息检出度从0.1逐步增长到0.9,估算流域生物信息流的99.9%置信区间逐渐从0.67—0.86(最大偏离16.25%)收缩到0.7867—0.8067(最大偏离1.66%),即随着样点生物信息检出度的增长估算流域生物信息流的估值区间逐渐集中于实际流域生物信息流水平(图2)。

图2 不同样点生物信息检出度下(B组)估算流域生物信息流值的概率分布Fig.2 Probability distributions of estimated watershed biological information flow (WBIF) in different biological information detection efficiency (BIDE) conditions at sampling sites (group B)B组,上下游样点分别有生物信息1000种、900种,实际流域生物信息流水平为0.8,样点生物信息检出度为变量

2.2 实际流域生物信息流状况对估算流域生物信息流的影响

模拟计算显示,上下游样点分别有生物信息1000种、900种的条件下,在样点生物信息检出度为0.1时,(1)随着实际流域生物信息流从0.1增长到0.9,估算流域生物信息流的最优估值基本稳定在偏小0.02左右,但其偏离程度在逐步减小(从偏离20%到偏离趋近于0%),即随着实际流域生物信息流的增长估算流域生物信息流的最优估值对实际流域生物信息流的偏离程度逐渐减小；(2)随着实际流域生物信息流从0.1增长到0.9,估算流域生物信息流的99.9%置信区间幅宽逐渐先增大再减小(从0.14(0.02—0.16)逐步增大到0.25(0.34—0.59)再逐步缩小到0.1(0.8—0.9)),最大幅宽出现在实际流域生物信息流为0.5的时候,但其最大偏离程度一直在逐步减小(从最大偏离80%到最大偏离11%),即随着实际流域生物信息流的增长估算流域生物信息流的估值区间幅宽先增大再减小,但整体上逐渐相对集中于实际流域生物信息流水平(图3)。

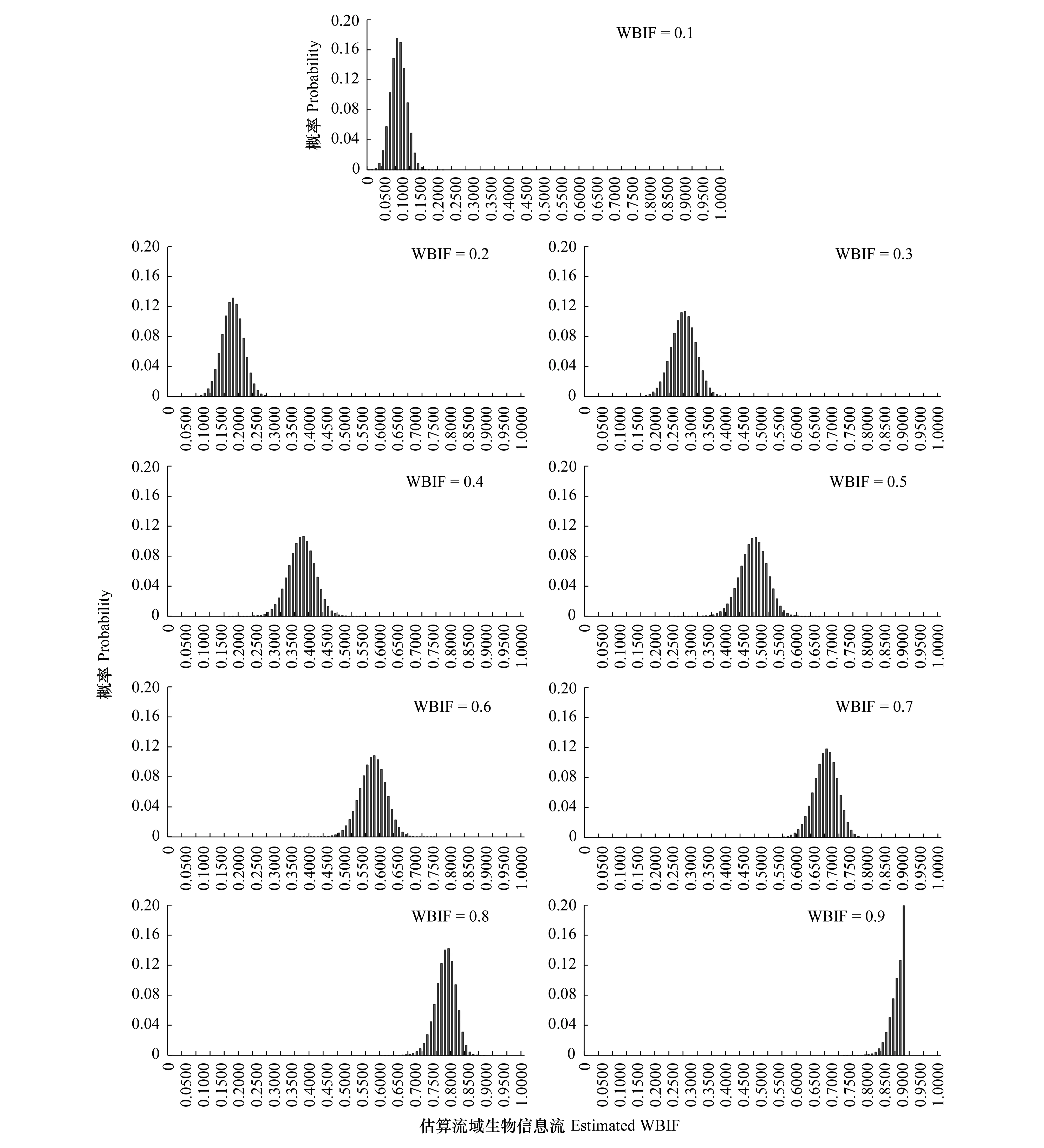
图3 不同实际流域生物信息流下(C组)估算流域生物信息流值的概率分布Fig.3 Probability distributions of estimated watershed biological information flow (WBIF) in different actual WBIF conditions (group C)C组,上下游样点分别有生物信息1000种、900种,样点生物信息检出度为0.1,实际流域生物信息流为变量

在样点生物信息检出度为0.5时,(1)随着实际流域生物信息流从0.1增长到0.9,估算流域生物信息流的最优估值从偏小0.004增大到偏小0.008再减小到0,但其偏离程度在逐步减小(从偏离4%到偏离趋近于0%),即随着实际流域生物信息流的增长估算流域生物信息流的最优估值对实际流域生物信息流的偏离程度逐渐减小；(2)随着实际流域生物信息流从0.1增长到0.9,估算流域生物信息流的99.9%置信区间幅宽逐渐先增大再减小(从0.05(0.068—0.118)增大到0.084(0.446—0.53)再缩小到0.03(0.87—0.9)),最大幅宽出现在实际流域生物信息流为0.5的时候,但其最大偏离程度一直在逐步减小(从最大偏离32%到最大偏离3.3%),即随着实际流域生物信息流的增长估算流域生物信息流的估值区间幅宽先增大再减小,但整体上逐渐相对集中于实际流域生物信息流水平(图4)。

图4 不同实际流域生物信息流下(D组)估算流域生物信息流值的概率分布Fig.4 Probability distributions of estimated watershed biological information flow (WBIF) in different actual WBIF conditions (group D)D组,上下游样点分别有生物信息1000种、900种,样点生物信息检出度为0.5,实际流域生物信息流为变量

2.3 上下游样点生物信息种类数相对关系对估算流域生物信息流的影响

模拟计算显示,上下游样点生物信息种类数对调(分别为900种、1000种)之后,在实际流域生物信息流水平在0.5的时候,(1)随着样点生物信息检出度从0.1逐步增长到0.9,估算流域生物信息流的最优估值从0.4778(偏离4.44%)逐步增长到0.4975(偏离0.5%),即随着样点生物信息检出度的增长估算流域生物信息流的最优估值逐渐趋近于实际流域生物信息流水平,但相比于上下游样点生物信息种类数对调之前(上游1000种,下游900种)的最优估值的偏离程度有所增大；(2)随着样点生物信息检出度从0.1逐步增长到0.9,估算流域生物信息流的99.9%置信区间逐渐从0.3222—0.6(最大偏离35.56%)收缩到0.4802—0.5111(最大偏离3.96%),即随着样点生物信息检出度的增长估算流域生物信息流的估值区间逐渐集中于实际流域生物信息流水平,但相比于上下游样点生物信息种类数对调之前(上游1000种,下游900种)的估值区间的幅宽和最大偏离程度都有所增大(图5)。

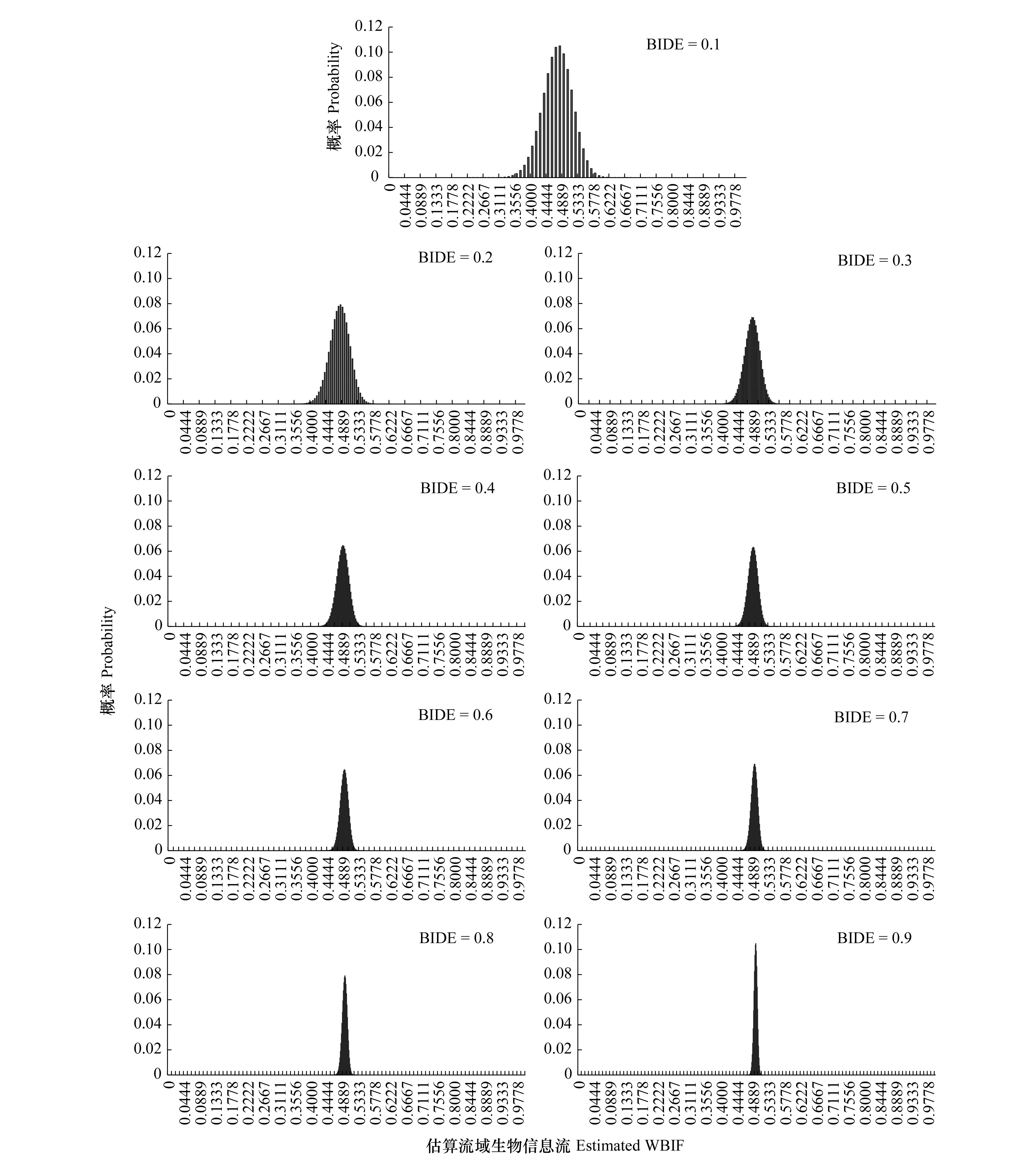
图5 不同样点生物信息检出度下(E组)估算流域生物信息流值的概率分布Fig.5 Probability distributions of estimated watershed biological information flow (WBIF) in different biological information detection efficiency (BIDE) conditions at sampling sites (group E)E组,上下游样点分别有生物信息900种、1000种,实际流域生物信息流水平为0.5,样点生物信息检出度为变量

模拟计算显示,上下游样点生物信息种类数对调(分别为900种、1000种)之后,在样点生物信息检出度为0.5的时候,(1)随着实际流域生物信息流从0.1逐步增长到0.9,估算流域生物信息流的最优估值从偏小0.0044(偏离4.40%)逐步增长到0.0089(偏离2.97%)然后再缩小到0.0067(偏离0.74%),即随着实际流域生物信息流的增长估算流域生物信息流的最优估值对实际流域生物信息流的偏离程度逐渐减小,但相比于上下游样点生物信息种类数对调之前(上游1000种,下游900种)的最优估值的偏离程度有所增大；(2)随着实际流域生物信息流从0.1逐步增长到0.9,估算流域生物信息流的99.9%置信区间幅宽从0.0543(最大偏离33.3%)逐渐先增大到0.0934(最大偏离11.56%)再减小到0.0666(最大偏离4.93%),即随着实际流域生物信息流的增长估算流域生物信息流的估值区间幅宽先增大再减小,但整体上逐渐相对集中于实际流域生物信息流水平,相比于上下游样点生物信息种类数对调之前(上游1000种,下游900种)的估值区间的幅宽和最大偏离程度都有所增大(图6)。

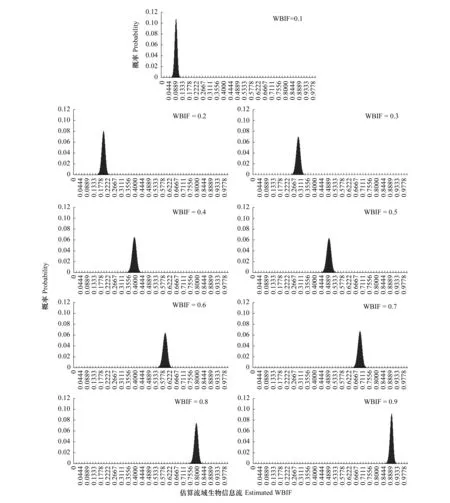
图6 不同实际流域生物信息流下(F组)估算流域生物信息流值的概率分布Fig.6 Probability distributions of estimated watershed biological information flow (WBIF) in different actual WBIF conditions (group F)F组,上下游样点分别有生物信息900种、1000种,样点生物信息检出度为0.5,实际流域生物信息流为变量

3 讨论

3.1 样点生物信息检出度同时影响了流域生物信息流估算的准确度和精密度

随着样点生物信息检出度的增长估算流域生物信息流的最优估值逐渐从偏低趋近于实际流域生物信息流水平。基于A组和B组参数的模拟计算结果显示,上下游样点分别有生物信息1000种、900种的条件下,在实际流域生物信息流水平在0.5的时候,随着样点生物信息检出度从0.1逐步增长到0.9,估算流域生物信息流的最优估值从0.48(偏离4%)逐步增长到0.4978(偏离0.44%)；在实际流域生物信息流水平在0.8的时候,随着样点生物信息检出度从0.1逐步增长到0.9,估算流域生物信息流的最优估值从0.79(偏离1.25%)逐步增长到0.7978(偏离0.275%)。在样点生物信息检出度的各个水平条件下,估算流域生物信息流的最优估值对实际流域生物信息流都偏小,并且样点生物信息检出度越高估算流域生物信息流的最优估值对实际流域生物信息流的偏小程度越小,估算准确度越高。

随着样点生物信息检出度的增长估算流域生物信息流的估值区间逐渐集中于实际流域生物信息流水平。基于A组和B组参数的模拟计算结果显示,上下游样点分别有生物信息1000种、900种的条件下,在实际流域生物信息流水平在0.5的时候,随着样点生物信息检出度从0.1逐步增长到0.9,估算流域生物信息流的99.9%置信区间逐渐从0.34—0.59(最大偏离32%)收缩到0.4822—0.51(最大偏离3.56%)；在实际流域生物信息流水平在0.8的时候,随着样点生物信息检出度从0.1逐步增长到0.9,估算流域生物信息流的99.9%置信区间逐渐从0.67—0.86(最大偏离16.25%)收缩到0.7867—0.8067(最大偏离1.66%)。估算流域生物信息流的99.9%置信区间内的概率分布近似正态分布,但向偏小的方向滑动(图1、图2),置信区间上限的最大偏离程度小于置信区间下限的最大偏离程度；样点生物信息检出度对估算流域生物信息流的99.9%置信区间内的概率分布对实际流域生物信息流的偏离程度有影响,检出度越高估算流域生物信息流的99.9%置信区间越小,对实际流域生物信息流的偏小程度也越小,估算精密度越高。

样点生物信息检出度越高,对样点生物信息的刻画越精确,对基于样点生物信息检出度的相关评估结果的估算也越精确。调查样点的生物信息检出是整个研究江段流域生物信息流估算的基础[3],决定了用eDNA监测水生生物多样性的可监测距离的估算[11]。前人的研究中,对流水水体中的水生生物的可监测距离的估算有各种各样的数值,从小几十米[18,20],到几百米、数公里[21—22],再到上百千米[16]都有,导致这一结果差异的涉及到eDNA的产生、输移、吸附、沉积、再悬浮、降解等一系列动力学过程[13—14],受各种各样的因素影响[17,20,23—24],也会有样点生物信息检出度差异对其估算结果的影响。为了推动基于eDNA技术的研究具有更好的可靠性和可重复性,标准化的研究方案和论文研究细节说明已被大家所注意到,但截至目前大家所关注的主要是采样点状况、采样技术方案、采样环境条件、采样时间设置、样品处理方式、污染控制状况、样品存储和运输条件、PCR条件等[25—28],较少关注平行样对研究结果影响的评估,以至于大家对用eDNA技术调查结果不做评估地直接展示[29—30]。因此,本研究在此强调,对各eDNA监测研究所获得的可监测距离在采信之前需要给予相应基于样点生物信息检出度的可信度评估,同时也建议未来基于eDNA技术的研究对各自的研究结果进行可信度评估。

3.2 基于流域生物信息流估算可信度目标对样点生物信息检出度进行控制

为了得到可信的流域生物信息流估算结果,有必要基于流域生物信息流估算可信度目标进行样点生物信息检出度的控制。在实际调查应用中,调查到或没调查到某一目标对实际该目标存在与否的判断只是在一个概率意义上成立,当某一情况的可信度达到某一阈值其结果才可信或可用。与之相应,在流域生物信息流实际调查评估中,估算出的两个样点间的流域生物信息流值对实际流域生物信息流的表征也只是在一个概率意义上成立,当某一估算结果的可信度达到某一阈值其结果才可信或可用。假设我们设流域生物信息流估算的最优估值对实际值的偏离不超过1%,且流域生物信息流估算值的99.9%置信区间对实际值的最大偏离不超过5%,为流域生物信息流估算可信度的目标。那么,在上下游样点分别有生物信息1000种、900种的,实际流域生物信息流水平在0.5左右的条件下,样点生物信息检出度应控制在0.8以上(图1)；在上下游样点分别有生物信息1000种、900种的,实际流域生物信息流水平在0.8左右的条件下,样点生物信息检出度应控制在0.5以上(图2)。

2020年9月在武汉江段一个调查样点的eDNA调查结果显示,可用eDNA(单引物mlCOIintF/ jgHCO2198R)调查到的鱼类物种最优估计约99种,单样品eDNA的鱼类物种检出能力约为26种,检出效率约为25.8%,在50%的检出度目标下,需要约3个平行样,在80%的检出度目标下,需要约10个平行样[19]。如果在这一时段需要在长江干流武汉江段进行eDNA采样估算以鱼类为指标的流域生物信息流,其中假设采样距离设置为10km,实际流域生物信息流预估为0.8左右,那么为了获得一个可信的流域生物信息流正式估算值,每个样点需采的平行样数量不应少于3个；假设如果采样距离设置为30km,实际流域生物信息流预估为0.5左右,那么为了获得一个可信的流域生物信息流正式估算值,每个样点需采的平行样数量不应少于10个。

在两个采样点间的实际流域生物信息流值较低的情况下,应适当提高平行样数量。实际流域生物信息流大小不影响样点生物信息检出度对估算流域生物信息流的影响规律(图1、图2对比),但影响了估算流域生物信息流的估算(图3、图4)。流域生物信息流本身的值越低,采样和计算中的不确定性产生的影响就越大；流域生物信息流本身的值越高,采样和计算中的不确定性产生的影响就越小。用模拟计算结果来讲,估算流域生物信息流的最优估值随着实际流域生物信息流降低而逐渐偏离(偏小)实际流域生物信息流水平(图3),估算流域生物信息流的99.9%估值区间的最大偏离程度随实际流域生物信息流降低而逐渐增大,估值区间相对于实际流域生物信息流水平的集中度逐渐降低(图4),所以在实际流域生物信息流的值较低时,应适当提高平行样数量,以通过提高样点生物信息检出度来提高估算流域生物信息流的精确度。2019年在青藏高原一个小型河流的流域生物信息流量化研究结果显示,春季封冻期、夏季降雨天、秋季多云天的流域生物信息流估算结果分别为75.86%、97.41%、96.07%每千米[11],如果以10km2为间隔设置样点,其样点间流域生物信息流估值分别为6.31%、76.92%、66.97%,那么为了获得一个可信的流域生物信息流正式估算值,各样点的信息检出度分别需要达到98%、50%、60%左右。

在上游样点生物信息种类数小于下游样点生物信息种类数的情况下,应适当提高平行样数量。上游样点的生物信息种类与下游样点的生物信息种类的相对关系,并不影响样点生物信息检出度和实际流域生物信息流对估算流域生物信息流的影响规律,但影响了估算流域生物信息流的估算。由于在上游样点生物信息种类数小于下游样点生物信息种类数的情况下所估算的流域生物信息流估值比在下游样点生物信息种类数小于上游样点生物信息种类数的情况下所估算的流域生物信息流估值相对流域生物信息流实际值有更大的最优估值偏离(偏小)程度(图1、图5对比)和更大的99.9%估值区间的幅宽和最大偏离程度(图4、图6对比),所以在上游样点生物信息种类数小于下游样点生物信息种类数时,应适当提高平行样数量,以通过提高样点生物信息检出度来提高估算流域生物信息流的精确度。由于流域生物信息流会增加输入水体的生物信息种类[3—4],因此通常情况下,上游样点的生物信息种类会少于下游样点的生物信息种类,在这种条件下,估算流域生物信息流最优估值对实际流域生物信息流的偏小程度更大,估算流域生物信息流估值区间的幅宽和最大偏离程度也更大。由于流域生物信息流对所输入水体的生物信息种类的增加在持续的向下游输移过程中是非累计的[3],所以河流的干支流交汇处的生物信息种类会比交汇处下游较远处的生物信息种类要多,在这种条件下,估算流域生物信息流最优估值对实际流域生物信息流的偏小程度会减小,估算流域生物信息流估值区间的幅宽和最大偏离程度也会减小。另外,随着水体理化环境的转变,流域生物信息流中的有效流域生物信息流部分会被环境过滤效应所过滤掉,导致上游样点的生物信息种类会多于下游样点的生物信息种类[3],在这种条件下,估算流域生物信息流最优估值对实际流域生物信息流的偏小程度会减小,估算流域生物信息流估值区间的幅宽和最大偏离程度也会减小。因而,相比于在河流交汇处及河流理化环境状况急剧转换处,在通常的河流条件下,流域生物信息流调查估算中需要更多的平行样。

3.3 对流域生物信息流估算结果进行后验概率评估

在上下游样点生物信息种类数相对关系确定、实际流域生物信息流确定、样点生物信息检出度确定的情况下,理论上所可得的估算流域生物信息流的值依然是分布在某一特定估值区间,而非一个确切值。虽然说通过基于流域生物信息流估算可信度目标的样点生物信息检出度控制可以提高理论上所可得的估算流域生物信息流的估值区间的集中度,进而使得流域生物信息流估算值对实际值有较好的近似程度,但在实际应用中还是有必要给出这个流域生物信息流估值所对应的实际流域生物信息流(区间)及相应后验概率,以保障其结果的科学性严谨性,给不同研究之间的横向比较提供科学可行合理可靠的基础。

在实际调查评估工作中,上下游样点生物信息种类数可以通过各调查样点一定数量的平行样的调查结果的物种积累曲线的分析而估算获得[19],各调查样点的样点生物信息检出度可以通过调查所得的生物信息种类数除以各相应调查样点的生物信息种类数而计算获得[19],估算流域生物信息流的值可以通过上下游共有生物信息种类数除以上游样点生物信息种类数而计算获得[3],然后可以根据模拟计算公式组进行相应的模拟计算,再通过后验概率计算实际流域生物信息流状况及其概率分布。

流水水体中,自上游到下游的流域生物信息流过程十分复杂,涉及到eDNA的释放、稀释、吸附、再悬浮、输移、降解等过程[13—15]。有一种方向是朝着弄清楚机理的方向努力,通过受控实验弄清环境因子对流域生物信息流过程中各环节的影响,再通过各环境因子的参数化、流域生物信息流过程各环境的模型化来推动对整个流域生物信息流的理解和量化[17,31—33]。我们认为,还可以有另外一个方向,即暂时先把流域生物信息流的复杂过程打包成黑箱,接受不确定性控制不确定性量化不确定性,通过输入和输出的量化分析,推进流域生物信息流研究的应用和发展。这即是我们所提出的流域生物信息流分析框架的处理问题方式[3,11],也是本研究的目的。

4 结论

本文针对平行样的增减是否会显著改变以及会如何改变流域生物信息流的估算结果这一问题,通过对问题进行简化而转化为检出度是否会以及会如何影响估算流域生物信息流的问题,进而通过模拟计算对其进行了探讨。模拟计算结果显示,估算流域生物信息流的最优估值小于实际流域生物信息流,随着样点生物信息检出度(即平行样数量)的增长估算流域生物信息流的最优估值逐渐趋近于实际流域生物信息流值,估算流域生物信息流的估值区间逐渐集中于实际流域生物信息流值,即样点生物信息检出度越高(平行样越多)估算流域生物信息流的准确度和精密度越高。另外,实际流域生物信息流大小、上下游样点生物信息种类数相对关系均对估算流域生物信息流的准确度和精密度有明确影响：实际流域生物信息流越大估算流域生物信息流的准确度和精密度越高,上游样点的生物信息种类多于下游样点的生物信息种类时的估算流域生物信息流的准确度和精密度相对更高。在实际应用中,为了提高流域生物信息流估算结果的可靠性,有必要基于流域生物信息流估算可信度目标进行样点生物信息检出度的控制,并且对流域生物信息流估算结果进行后验概率评估。