基于改进蚁群算法的现代物流运输最优路径规划方法

曾莎莉

（中国石油集团川庆钻探工程有限公司重庆运输总公司，重庆 400021）

0 引言

现代物流运输最关键的问题就是从始发地到终点之间路径的选择，运输油耗是现代物流运输的主要成本。在规定的时间内选择路程最短、路况最好的道路作为现代物流运输最优路径，以此将现代物流运输成本降到最低，这样既能满足客户在运输时间方面的需求，还能使物流企业利益最大化。近年来，现代物流运输行业作为“第三利益源泉”，对经济发展的带动作用逐渐凸显，物流行业在市场经济中的地位也有了明显提高，如何选出最优的物流运输路径成为现代物流行业所面临的重要难题。在最快时间选出现代物流运输最优路径，对降低现代物流运输成本、节省现代物流运输时间、提高现代物流运输服务质量具有重要作用。现代物流企业目前所采用的最优路径规划方法在实际应用中物流运输时间比较长，尤其是对于井场货物运输，运输路程比较长，经过的运输点比较多，现有的路径规划方法所规划的路径耗时较长，无法满足井场货物运输时间需求。为此，本文提出基于改进蚁群算法的现代物流运输最优路径规划方法。

1 基于改进蚁群算法的现代物流运输最优路径规划方法设计

1.1 确定现代物流运输路径冲突分流点

井场货物运输过程中从起发地点到目的地点中间存在多个运输节点，现代物流运输最优路径规划问题就是对物流节点合理选择的问题，物流节点的物理属性需要符合实际情况，也就是井场货物运输路径中所有的路径节点不能出现冲突。以有向图规划理论作为理论基础，对井场货物运输路径中的物理冲突分流点进行确定。按照物流运输路径交叉口到井场货物运输起点的距离将物流运输节点进行标记，并建立井场货物运输有向图，在建立的有向图中选取井场物流运输起点到终点的中间节点作为核心节点，用节点

G

表示，其代表井场货物运输最优路径的中央位置。然后，在节点与节点之间设置物流方向，以此突出井场货物运输路径的单向性特征。将每个道路节点的真实属性在有向图中标记，包括道路交叉口坐标、交通方向等。最后，在有向图中井场货物运输路径长度需要与各个起始节点距离长度呈对应关系。在建立的井场货物运输的有向图中确定井场货物运输路径的冲突点，并将各个冲突点用节点

H

表示，在规划井场货物运输最优路径时不考虑冲突点作为最优路径节点，以此确保规划的井场货物运输最优路径中点位均衡，并且没有路径节点冲突。

1.2 现代物流运输最优路径问题描述

井场货物运输路径规划不仅要考虑到路径交叉路口物理属性，还要考虑到井场货物运输道路长度、运输时间、运输路径路况等运输逻辑属性。两个相邻的路径节点连接形成有向图节点路线，将相邻路径节点的距离、道路交通情况、道路运输时间等节点属性值进行标准化，以此确定井场货物运输路线权值，按照权值大小将相邻节点连接路线进行排序，以此将上文建立的井场货物运输有向图转化为带权有向图，其用公式（1）表示：

式（1）中，

A

表示井场货物运输路径带权有向图，

W

表示井场货物运输路径中所包含的路径节点集合，[

B

]表示井场货物运输路径中所包含的连接两个路径节点的边的集合。假设井场货物运输路径中所包含的路径节点集合中的起始节点为

q

，井场货物运输路径中所包含的路径节点集合中的终点节点为

p

，则现代物流运输最优路径规划问题可以描述为在货物运输路径带权有向图

A

中，选择出从起始节点

q

到终点节点

p

的一条权值最小的路径，且该路径中不包含冲突点

H

。

1.3 基于改进蚁群算法的现代物流运输最优路径规划

井场货物运输最优路径规划的问题与蚁群觅食行为相似，因此现代物流运输最优路径规划中常采用蚁群算法，通过蚁群之间信息传递来规划现代物流运输最优路径。但是，蚁群算法所规划的路径在实际应用中常出现道路不通畅的情况，此次对蚁群算法进行改进，利用改进蚁群算法规划现代物流运输最优路径。

将井场货物运输起点

q

作为蚁群寻找食物起点，即蚂蚁巢穴，将井场货物运输终点

p

作为蚂蚁所寻找食物地点，蚁群在寻找事物过程中根据自身条件和外部条件的变化随时更换路线，假设蚂蚁共有

n

只，每只蚂蚁寻找食物的路径用公式（2）表示：

式（2）中，

h

表示蚂蚁寻找食物路径，

n

表示蚂蚁的数量，

s

表示蚂蚁从蚂蚁巢穴到节点

i

之间的距离，

s

表示蚂蚁从节点

i

到食物之间的距离。利用公式（2）表示蚂蚁寻找食物的路径。将运输时间、运输成本及路畅程度作为约束条件，从众多蚂蚁觅食路径中选取运输时间最短、成本最低、路畅最好的路径作为最优路径，其中运输时间约束条件用公式（3）表示：

式（3）中，

t

(

j

)表示蚂蚁觅食时间因子，

t

表示蚂蚁觅食路径所需时间，

t

表示蚂蚁觅食过程中允许的最长时间上限。该约束条件中，蚂蚁觅食路径所需时间

t

不能超过蚂蚁觅食过程中允许的最长时间上限

t

。运输成本约束条件用公式（4）表示：

式（4）中，

l

(

j

)表示蚂蚁觅食所消耗体力因子，即经常货物运输成本因子；

f

表示蚂蚁觅食路径所需要消耗的体能，即井场货物运输所需要的运输成本；

f

表示蚂蚁觅食过程中允许的最大消耗体能，即井场货物运输最大预估运输成本。该约束条件中，蚂蚁觅食路径所需要消耗的体能不能超过蚂蚁觅食过程中允许的最大消耗体能。路畅约束条件用公式（5）表示：

式（5）中，

r

(

j

)表示蚂蚁觅食路径路畅因子；

r

表示蚂蚁觅食路径实际路畅程度，即井场货物运输实际路畅程度；

r

表示蚂蚁觅食过程中路畅最低容忍度，即井场货物运输所能允许的最差路畅程度。按照以上3 个约束条件对每个蚂蚁觅食路径进行约束，选择出符合上述3 个约束条件的路径，在符合条件的路径中对每个路径的时间、成本、路畅3 个指标权重进行确定，然后按照权重从大到小的顺序对路径进行排序，以权重最大的路径作为蚂蚁觅食最优路径，以此结束改进蚁群算法运算。将计算到的路径在上文建立的井场货物运输有向图中进行标识，作为井场货物运输最优路径，以此完成基于改进蚁群算法的现代物流运输最优路径规划。

2 实验论证分析

实验以某井场货物作为实验对象，将井场货物从井场分别运输到A、B、C、D、E、F、G、H 8 个地点，利用此次设计方法与传统方法对该井场货物运输最优路径进行规划。建立了8 个井场货物运输有向图，节点数量分别为11 个、14 个、16 个、15 个、18 个、19个、18 个、21 个，冲突节点数量分别为3 个、2 个、6个、4 个、3 个、1 个、2 个、4 个，利用公式（2）对每个井场货物运输路径进行确定，再利用约束条件对路径进行约束，根据实际情况确定每个路径的权值，最终选择了最优路径，具体情况如表1 所示。

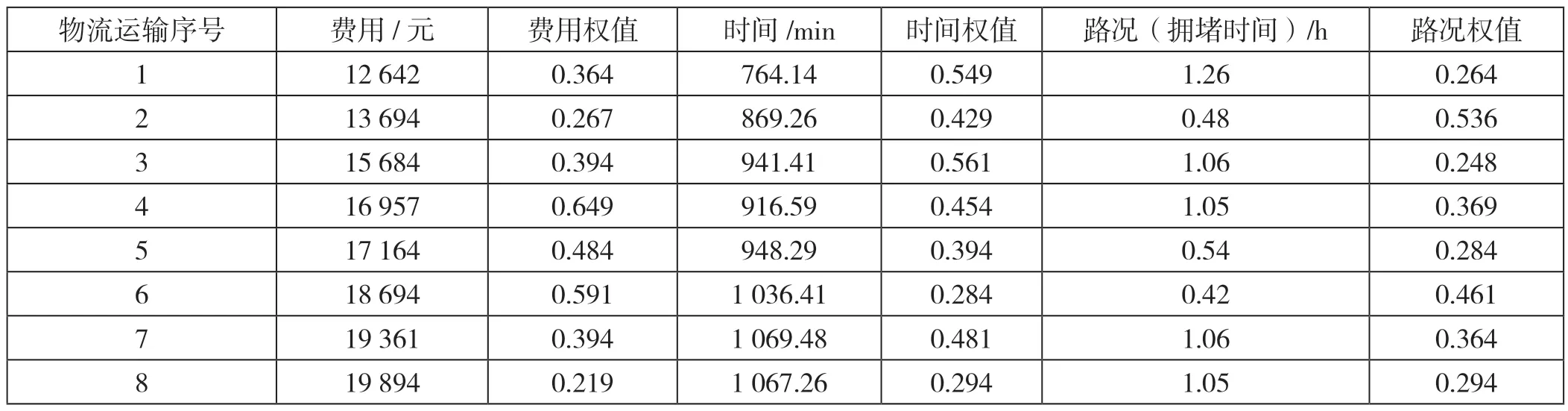
表1 井场货物运输最优路径

按照规划的物流运输路径对井场货物进行运输，对两种方法规划路径的实际运输时间进行记录，将其作为实验数据，对两种方法的可靠性和有效性进行评价，实验结果如表2 所示。

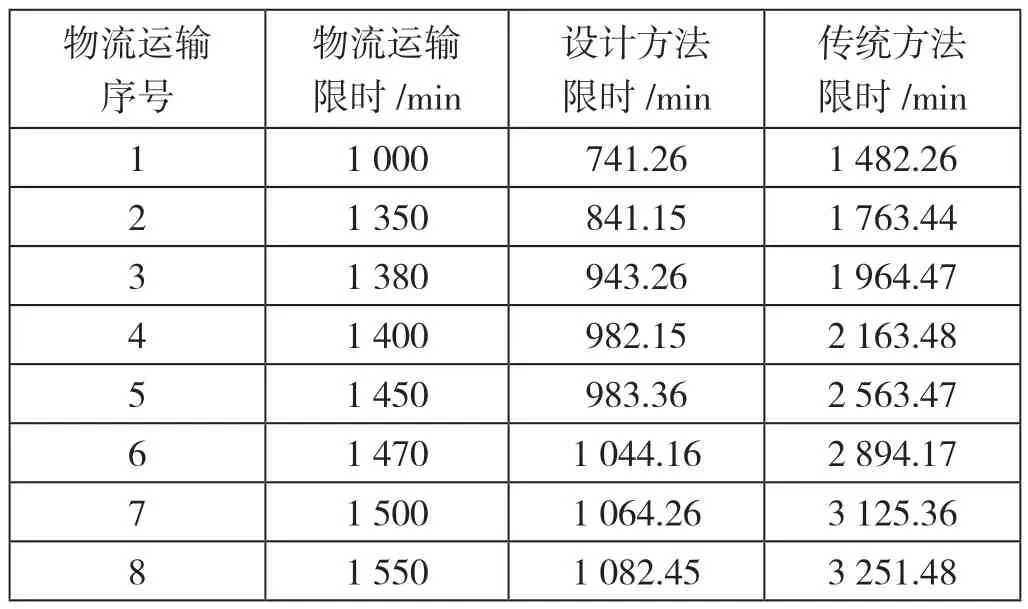
表2 两种方法应用下物流运输时间对比

从表2 的数据中可以看出，车辆按照此次设计方法规划的物流运输路径所花费的运输时间比较短，可以在规定时间内将货物运输到指定地点，最快的货物运输时间提前了43 min；车辆按照传统方法规划的物流运输路径所花费的运输时间远远长于设计方法，并且没有在规定时间内将货物运输到指定地点，超时的最长时间为117 min。这是因为本文提出的基于改进蚁群算法的现代物流运输最优路径规划方法在考虑到路径问题的同时还考虑了物流运输路况问题，因此实验证明了此次设计方法能够准确规划出现代物流运输最优路径，相较于传统方法，基于改进蚁群算法的现代物流运输最优路径规划方法的可靠性和有效性更好。

3 结语

此次利用改进蚁群算法设计了一种新的现代物流运输最优路径规划方法，对井场运输时间、成本及路况进行约束，寻找出路径最短、路况最好、成本最低的路径作为物流运输最优路径，有助于降低现代物流运输成本，缩短井场货物运输时间，实现在规定时间内将货物运输到规定地点。由于个人水平有限，本文提出的规划方法尚未在现代物流运输路径规划中进行大量实践应用，对于改进的蚁群算法可能存在不足之处，今后仍会在该方面进行深入研究，为现代物流运输行业发展提供可靠的理论支撑。