基于无监督学习的高分辨光声重建

卢孟阳，李博艺，朱志斌，刘成成，刘 欣，他得安,3

（1.复旦大学工程与应用技术研究院，上海 200433；2.河西学院物理与机电工程学院，甘肃张掖 734000；3.复旦大学生物医学工程中心，上海 200433）

0 引言

光声断层成像（Optoacoustic Tomography,OAT）作为近年来迅速发展的非侵入式生物医学成像方法[1-3]，凭借其高对比度和深穿透的成像优势，在基础生物医学、临床应用等研究领域具有广阔的应用前景。需要指出的是OAT 是一种由光激发和超声检测方式实现的成像技术，在成像深层组织区域时，依赖于声学反演方法，其最终成像的空间分辨率受声学衍射极限所限制。在实际应用中，OAT 成像深度与空间分辨率之间大约为100～200 的倍数关系[4]，致使其对较深层组织进行成像时，难以对细胞结构、微血管结构等进行有效解析。

随着医学影像技术的发展、相关硬件设备的不断完善，基于并行超声阵列的OAT 系统能够实现快速三维成像[5]；并且基于该系统，通过轻微移动检测阵列可获得大量光声断层图像序列，进而提高成像分辨率[6]。Dean-Ben 等[7]进一步提出了对流动的单个吸收体进行动态OAT 成像的方法。在此基础上，借鉴于光学显微成像中基于定位方法的超分辨荧光显微成像技术，例如随机光学重构显微成像技术（Stochastic Optical Reconstruction Microscopy,STORM）、光激活定位显微成像技术（Photoactivated Localization Microscopy,PALM）等[8-9]，研究者们提出了基于定位方法的高分辨光声断层成像技术[10-14]。简而言之，该技术通过对连续采集的光声断层图像序列中的稀疏吸收体粒子使用局部最大值法进行定位[12]，并叠加得到的所有定位点从而获得最终的高分辨率图像。为了进一步提高定位精度，Vilov等[13]提出将最大值定位在互相关图像上，即每个激发光获得的光声断层图像和点扩散函数（Point Spread Function,PSF）之间的二维互相关图像，以此来确定吸收体的位置，最终能够达到约78 µm 的横向分辨率[14]。

基于上述策略，能够有效提升光声断层成像的声学分辨率。但是基于现有定位方法实现OAT 高空间分辨率的同时，要求所使用的动态光声断层图像必须是稀疏的。因此，当对复杂结构进行成像时，为了确保能够捕获成像对象的完整结构，需要采集大量光声断层图像，因而限制了高分辨光声断层成像的时间分辨率。

近年来深度学习（Deep Learning,DL）技术大放异彩，凭借其强大的数据处理能力在各种任务上展现出极大的潜力。U-Net 作为一种有效的网络框架，在多种图像处理任务，特别是超分辨定位荧光显微成像领域，都展示了优异的性能。然而传统U-Net 的网络重建效果依赖于大量配对数据的使用，在一定程度上限制了该方法在定位任务上的应用。考虑到物理模型与深度学习方法相结合的有效性[15]，本文提出了一种结合物理PSF 模型与基于注意力机制的无监督网络方法（Phys-AU-Net）。

1 方法与数据

Phys-AU-Net 方法结合了PSF 模型和卷积神经网络用于实现衍射受限光声断层图像的高分辨重建。其中，引入PSF 物理模型，可以实现无监督学习，摆脱深度学习方法对数据标签的依赖问题；而其中的卷积神经网络具有强大的特征表达能力以及运算能力，可以完成对光声断层图像中密集吸收体的定位重建。因此，本文提出的Phys-AU-Net 方法，可以在仅以声衍射受限的光声断层图像作为网络训练数据的情况下，经迭代优化，实现准确的光声断层图像高分辨定位重建。

图1 展示了本文提出的结合PSF 模型的无监督高分辨重建网络的主要框架。图1 中，网络的输入，即Input I，为声衍射受限的光声断层图像，输出Output O 为网络重建得到的高分辨光声断层图像。与监督学习中网络隐含参数的更新取决于网络输出与标签数据的损失不同，本方法引入了PSF 物理模型，从而摆脱了对数据标签的依赖。具体而言，经网络处理后得到的高分辨光声断层图像会与PSF模型进行卷积操作模拟成像过程中的衍射受限问题，从而产生声学分辨率受限的光声断层图像。在网络训练时，通过计算该图像和输入光声断层图像之间的损失，反向回馈更新神经网络中的隐含参数，经过迭代优化，最终完成网络的训练。因此，该方法中PSF 模型参数的设置至关重要，决定着最终的成像性能以及实用性。

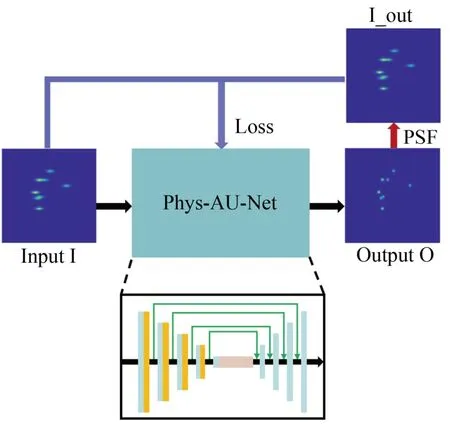
图1 无监督光声断层图像高分辨重建网络示意图 Fig.1 Schematic diagram of optoacoustic image high resolution reconstruction based on unsupervised strategy

1.1 Phys-AU-Net 网络结构

在具体实现中，所用到的卷积神经网络是基于U-Net 网络架构进行设计的，并引入了通道注意力模块。基于编解码结构的U-Net 网络能够对特征进行不同层次的处理，实现对图像数据深层抽象特征的提取。其中，通道注意力模块则可以区分每个特征的重要性，有利于网络学习更多关键性特征。Phys-AU-Net 网络的详细结构如图1 中黑色方框所示，编码器部分包含4 个下采样块，在每块中接连堆叠了卷积层、通道注意力层和下采样层；随后，在编码器之后连续堆叠了3 个卷积层以实现对抽象特征的表达及学习；解码器部分包含4 个上采样块，每块则由卷积层和上采样层堆叠而成。并且将跳跃连接应用于具有相同尺寸的上、下采样层之间实现特征的融合以及残差学习。在网络的最后使用一层卷积核为1×1 的卷积将提取到的特征图映射为通道数为1 的高分辨输出图像。在训练过程中，借助于PSF 模型以完成无监督式的特征学习。具体而言，网络输出的光声断层图像会进行PSF 卷积操作，从而产生相应的衍射受限图像，并计算该图像和输入数据之间的损失，反向回馈去更新网络中的隐含参数，经过迭代优化，最终完成模型的训练。该过程可以表示为

式中，H表示系统的点扩散函数，R则表示由神经网络学习到的映射函数，θ表示输入的衍射受限光声断层图像，†表示迭代过程。当优化完成时，基于训练得到的模型，则可以直接完成衍射受限光声断层图像的高分辨重建。

1.2 损失函数

在深度学习方法中，损失函数对网络最终的优化结果具有很大的影响。均方误差（Mean Squared Error,MSE）作为一种在DL 方法中广泛使用的损失函数，虽然能有效地完成网络的收敛，但是，MSE损失的最小化会导致重建结果的模糊[16]。因此，在本项工作中，添加了额外的正则化项来指导网络提高重建性能。考虑到所用光声断层图像的稀疏性，本文引入了L1正则化项，提高网络的收敛性以及对高频信息的学习能力。具体而言，在损失函数中引入了加权的Smooth_L1损失，用以解决L1的不光滑问题以及离群点梯度爆炸的问题。此外，参考Wang等[17]和Zhao 等[18]的工作，与其他损失函数相比，结构相似性指标（Structural Similarity,SSIM）对结构的变化更加敏感，这有助于确保图像之间的结构一致性。基于上述分析，在本工作中，将损失函数设计为三项损失的加权和，即MSE 损失LMSE、LSmooth_L1损失和SSIM 损失LSSIM，表达式为

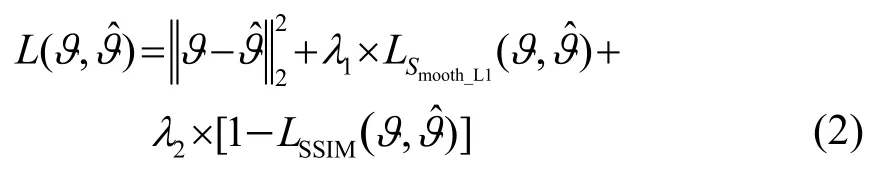
式中：ϑ表示输入的衍射受限的光声断层图像，表示网络的输出经PSF模型模拟产生的衍射受限光声 断层图像；即为MSE 损失LMSE；λ1和λ2代 表了对应损失项的权重参数，具体的数值是由多次实验对比选择出的，λ1=0.2，λ2=0.8。其中LSmooth_L1的具体计算方式为

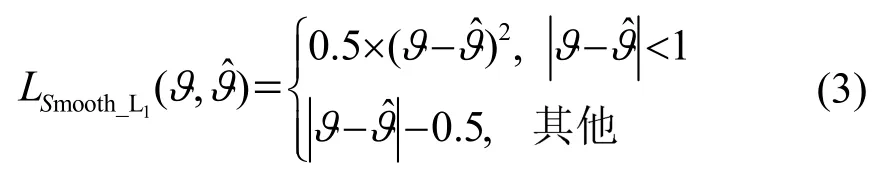
1.3 数据集

在本研究中所有的实验数据均是通过真实吸收体结构与成像系统PSF 进行卷积而产生的。具体实现可表示为

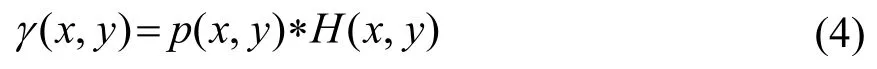
式中：Η（x,y）表示实验系统的点扩散函数，p（x,y）则表示包含吸收体真实分布的光声断层图像，γ（x,y）表示仿真的声衍射受限的光声断层图像。

为了使仿真数据尽可能地逼近真实实验条件下的分布，本文中所使用的PSF 的参数借鉴于Vilov 等[13]的研究。具体而言，在实验中，利用注射泵（KDS Legato 100）注射并控制直径为10 µm 的流动吸收体微珠（Microparticles GmbH），并使其在预先设置的回路中循环。回路中的5 个平行部分即为待成像的样本，具体的实验设置示意图可参考文献[13]。该实验装置的光声信号则由具备128 个阵元的线性电容式微机械超声换能器（Capacitive Micro-mechanical Ultrasonic Transducer,CMUT）阵列与多通道采集电子设备获取，然后经过传统的延迟求和算法重建得到流动吸收体微珠的光声断层图像。对获得的光声断层图像进行估计，具体而言，选取光声图像中单个吸收体的横向、纵向信号，并绘制其对应的归一化幅值曲线图，进而计算得到相应曲线的半高宽（Full Width Half Maximum,FWHM）。由此，得到的实验PSF 的横向FWHM 约为178 µm，轴向FWHM 约为137 µm。基于这些参数，就可以利用PSF 卷积法获取大量数据集。

根据式（4）的数据生成方式，在本文中所使用到的数据集如表1 所示，分为训练集和测试集。其中，训练集共1 200 帧具有不同噪声、不同密度的圆形吸收体图像，用于对网络的训练优化；测试集则包含圆形吸收体和血管结构的数据，用于验证已训练模型的性能。

表1 数值仿真产生的数据集 Table 1 Dataset generated by numerical simulation

（1）训练集

为满足训练数据的多样性，进而保证网络特征学习的有效性，在构建训练数据时，在128×128 像素的成像区域内，随机设置1～10 个吸收体，并添加信噪比（Signal to Noise Ratio,SNR）为5～30 dB 之间的高斯噪声。以这种模式共生成了1 200 帧衍射受限的光声断层图像，并以5：1 的比例划分为训练集和验证集。本工作所采用的部分训练集数据如图2 所示。

图2 训练数据 Fig.2 Training data

（2）测试集

测试集用于测试所提出网络模型的重建性能。在本文中涉及到评估Phys-AU-Net 对衍射受限光声断层图像中吸收体的定位效果，对高密度重叠吸收体的重建能力以及对复杂结构的高分辨重建性能。相应地，测试集的数据分布，由成像对象来划分大体可分为两类：不同密度、不同噪声情况下的简单圆形吸收体数据；不同分布的复杂血管结构数据，可用于测试模型的重建能力以及泛化能力。详细的测试数据如表2 所示。

表2 测试数据集的详细内容 Table 2 Testing dataset details

1.4 网络训练

经由数据仿真，通过Python 软件共生成了1 200例衍射受限的OAT 图像用于训练。网络训练总共设置了200 个周期，采用Adam 优化器进行优化，初始学习率设置为1×10-3，并采用了学习率衰减策略用于促进网络优化收敛。具体而言，在第50、100和150 个周期时，学习率依次衰减0.5。在实现中，上述过程均基于PyTorch 框架实现。本文相关网络的训练和测试过程均在在配备了NVidia Tesla V100 GPU（16 GB RAM）、2 个Intel Xeon Gold 6130（2.1 GHZ）和192 G DDR4 REG ECC 的服务器上实现。

2 结果与分析

2.1 解析能力的评估

首先，针对Phys-AU-Net 的解析能力进行了测试。具体而言，实验中，在水平、竖直方向各放置5 个间隔为50 µm 的吸收体进行成像，并且数据中添加了SNR 为15 dB 的高斯噪声。图3（a）显示了衍射受限的光声断层图像，即为网络的输入数据，可以看出在横向、纵向区域各吸收体之间均存在粘连，无法准确辨别区分；图3（b）表示了由Phys-AU-Net 重建得到的高分辨图像；图3（c）则展示了相应的真实吸收体分布；图3（d）和（e）则展示了图3（a）-（c）中红色点划线的归一化幅值对比图，其中（d）表示为纵向的对比图，（e）表示为横向的对比图。由重建结果可以分析出，相较于衍射受限图像，Phys-AU-Net 可以有效实现对衍射受限吸收体之间的解析，提高图像的分辨率。由曲线图可以看出，重建图像具有与真实分布极为接近的解析能力，有效提高了横向和纵向的分辨率，可以达到约50 µm。

图3 添加SNR 为15 dB 噪声时，吸收体间隔50 μm 时的 重建结果 Fig.3 Reconstruction results of absorbers at 50 μm interval after increasing Gaussian noise to SNR=15 dB

2.2 不同密度情况下的重建

对Phys-AU-Net 在不同密度情况下的高分辨重建性能进行了评估，结果如图4 所示。图4 显示的是不同密度情况下的重建结果，并与U-Net 方法进行了对比。图4（a）～4（d）展示了在测试过程中使用的具有不同密度分布的真实结构图，成像区域内分别随机放置了5、10、15、20 个吸收体。图4（e）～4（h）则展示了不同密度情况下的衍射受限图像，并且所有图像都添加了SNR 为15 dB 的高斯噪声。通过对比可以看出高密度情况下部分邻近的吸收体根本无法有效辨别，如图4（h）。图4（i）～4（l）则展示了Phys-AU-Net 方法重建得到的高分辨图像，图4（m）～4（p）展示了U-Net 网络的重建结果，图4 中右侧最后一列由上到下则分别为图4（d）、图4（h）、图4（l）、图4（p）中红色框内邻近吸收体的细节放大展示。

由图4 中的重建结果可以看出，本文提出的Phys-AU-Net 方法可以有效地实现不同密度情况下，对衍射受限光声断层图像的高分辨重建。在吸收体分布较为分散的情况下，图4（e）和4（f），能完整地恢复出吸收体的真实分布，背景也不存在噪声；即使是在吸收体分布更为密集、相互重叠的情况下，如图4（g）和4（h），相对于U-Net 方法，Phys-AU-Net 也能展现出优异的重建性能，能够有效解析邻近的吸收体，并且重建的吸收体结构与真实结构更为接近，如图4 中的细节放大图像所示。

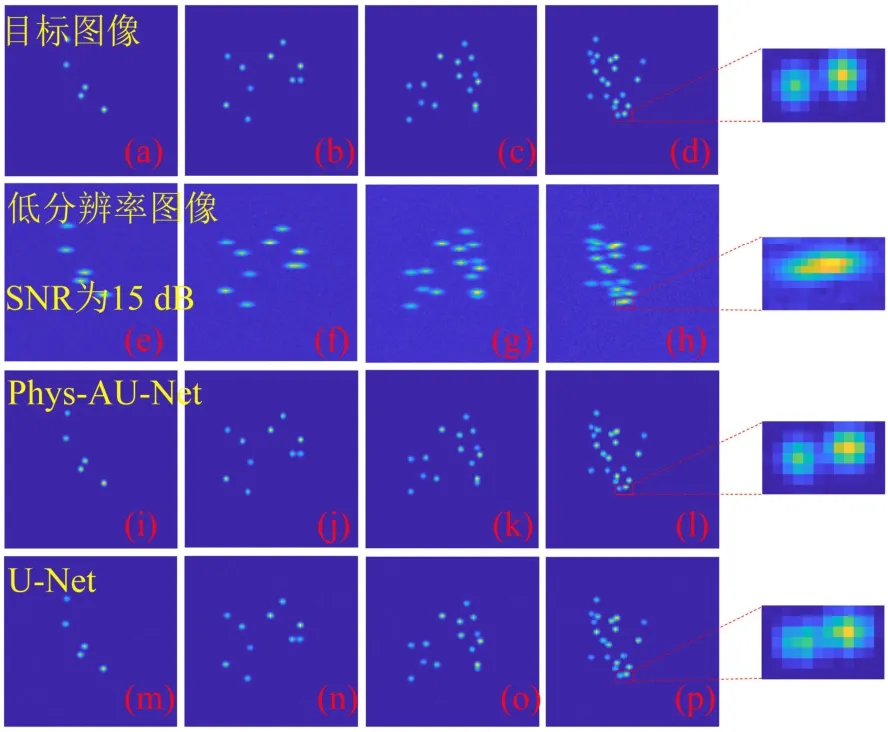
图4 不同密度情况下基于Phys-AU-Net 的吸声体高分辨 成像结果 Fig.4 High resolution imaging results of absorbers with different densities based on Phys-AU-Net

为了客观地评估重建效果，我们对随机选取的100 例包含5～25 个吸收体的衍射受限图像进行了定量统计分析，每帧图像添加了SNR 为15 dB 的噪声，计算了重建结果的SSIM 和峰值信噪比（Peak Signal to Noise Ratio,PSNR）指标，并与U-Net 网络进行了对比，相应的定量统计结果如表3 所示。分析表格可以得出，相较于U-Net 方法，Phys-AU-Net在SSIM 方面提升了43.5%，在PSNR 方面提升了11.2%。

表3 两种方法对100 例随机包含5～25 个吸收体的重建结果 的定量指标 Table 3 Quantitative indexes of two methods for reconstruction results of 100 trials with r andom 5～25 absorbers

2.3 不同信噪比下的重建

进一步针对该方法的噪声鲁棒性进行了实验验证。图5 展示了不同信噪比下各算法的高分辨重建结果对比。图5（a）～5（c）则分别表示了SNR 为15、10、5 dB 噪声情况下的衍射受限光声断层图像，图5（d）～5（f）则展示了由Phys-AU-Net 方法得到的重建结果，图5（g）～5（i）则显示了U-Net 网络的实验结果图。由重建结果可以看出，虽然随着SNR减小、噪声增强，Phys-AU-Net 方法对一些邻近吸收体的结构重建效果不佳，结果如图5（f）中所示。但是整体而言，该方法对噪声具有一定的鲁棒性，在不同SNR 情况下均能获得不错的重建效果，且重建图像的质量并未随着噪声的增加而大幅度降低，背景基本不存在噪声。相较而言，U-Net 网络的重建效果随着噪声程度的增强有较为明显的下降，背景中出现了噪声，结果如图5（i）所示。

图5 不同信噪比情况下基于Phys-AU-Net 的高分辨成像结果 Fig.5 High resolution imaging results based on Phys-AU-Net at different SNRs

2.4 复杂血管图像的重建

最后，针对复杂成像结构的高分辨重建进行了实验测试，结果如图6 所示。测试所用的复杂成像模型为具有不同粗细的血管结构。图6 展示了在成像复杂血管结构时，Phys-AU-Net 方法和U-Net 方法的重建结果对比。图6（a）～6（c）分别显示了SNR为15 dB 时，不同血管结构分布的衍射受限光声断层图像。可以看出血管的轮廓相对模糊，甚至细微的血管结构无法有效分辨；图6（d）～6（f）则展示了相应的由Phys-AU-Net 方法重建得到的高分辨结果；图6（g）～6（i）则分别表示了U-Net 方法的重建结果，图中部分血管无法有效恢复，且连续性较差；图6（j）～6（l）则显示了不同血管结构的真实分布。由图6 中的结果可以对比看出，提出的Phys-AU-Net方法能够一定程度上提高复杂血管图像的分辨率。虽然对于一些极细微的血管分支无法有效重建，但相较于U-Net 方法，Phys-AU-Net 方法能够实现对血管整体结构的高分辨重建，血管结构的连续性更好，并且具有更优的噪声去除效果。

图6 基于Phys-AU-Net 的血管模型的高分辨成像结果 Fig.6 High resolution imaging results of vascular structure based on Phys-AU-Net

针对复杂血管结构，进行了Phys-AU-Net 的噪声鲁棒性测试。为了客观地评估重建性能，对随机选取的40 例具有不同血管分布的衍射受限图像进行了定量统计分析，测试图像中分别添加了信噪比为5、10、15 dB 的噪声，并与U-Net 网络进行了对 比。重建结果的相应SSIM 和PSNR 指标如表4 所示。经分析可知，相较于U-Net 方法，Phys-AU-Net在不同信噪比时均具有更优的定量指标，并且相应指标数值并未随噪声的增强而有大幅度下降。由此可以说明，Phys-AU-Net 对噪声具有鲁棒性。

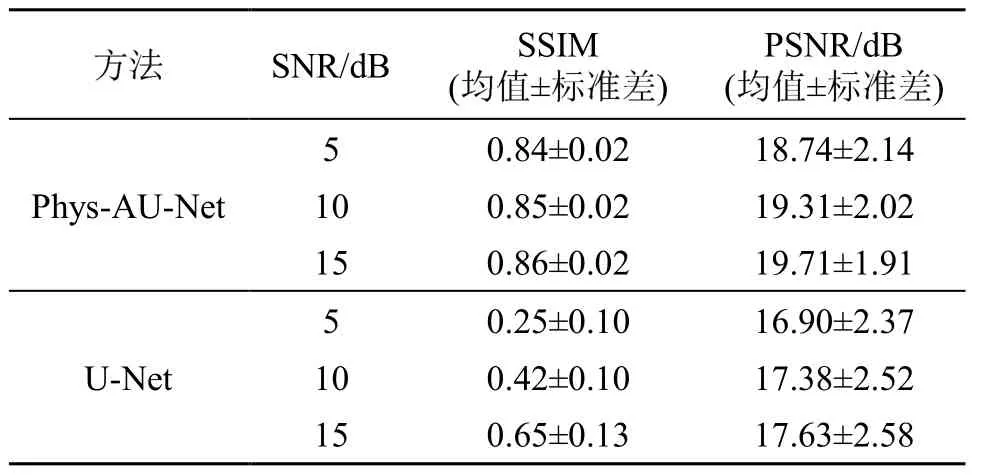
表4 不同信噪比，两种方法对40 例血管结构重建结果的 定量指标 Table 4 Quantitative indexes of two methods for reconstruction results of 40vascular trials at different SNRs

3 结论

本文提出了一种结合物理模型的无监督Phys-AU-Net 网络方法用于声衍射受限光声断层图像的高分辨重建。通过模型训练，Phys-AU-Net 能够学习声衍射受限光声断层图像与吸收体真实分布之间的映射关系，进而提升光声断层成像的空间分辨率，实现高分辨OAT 成像。

实验结果表明，本文提出的Phys-AU-Net 方法能有效提高光声断层图像的成像分辨率，可以达到约50 µm 的重建分辨率；能够很好地解析不同密度情况下的衍射受限光声断层图像，即使用于成像高度重叠的吸收体也具有很好的重建性能；另外，在信噪比为5、10、15 dB 时，Phys-AU-Net 依然能够较好地解析高密度情况下的吸收体，得到与真实分布相似的重建结果。这表明Phys-AU-Net 有着良好的抗噪性和解析高密度吸收体的能力。因而采用该方法可有效减少成像帧数及成像时间，并提高重建分辨率。另一方面，对于单帧复杂血管结构的高分辨重建，Phys-AU-Net 也能较好地恢复出与真实血管结构相似的结果。但是，对于极细微的血管分支，Phys-AU-Net 的解析能力会下降。因此还要继续改进该网络，以期进一步提高重建复杂血管的能力。目前的工作中，在设计PSF 模型时，仅针对单一实验情况进行了验证，尚未考虑复杂PSF 模型对成像结果的影响，相关内容会在未来进一步探究。另外，在本文中只进行了数值仿真实验，针对在体实验数据的性能探究会在今后的工作中进行。