基于IDA法的多跨连续刚构桥易损性分析
李思成,宁晓骏,薛挥杰
(昆明理工大学 建筑工程学院,云南 昆明 650500)
地震易损性指不同强度地震作用下工程结构发生各种破坏的概率,可从概率上定量衡量结构的抗震性能[1]。西南山区多处于地震带,刚构桥比连续梁桥具有更大的跨越能力,且具有结构简单,施工工艺较成熟等优势。由于该地区建设刚构桥较多,因此,有必要研究这类桥梁的地震易损性。曹操等人[2]利用有限元软件分析了连续梁桥地震作用时的影响,研究结果表明:在地震作用下,墩梁的约束方式对桥梁影响显著。肖永刚等人[3]采用时程分析法研究发现,大小井特大桥在受水平地震波作用时位移所受影响较大,受竖直地震作用时对轴力的影响较大。逐步增量动力分析法(incremental dynamic analysis,简称为IDA)是用于评估地震作用下结构响应参数化分析方法[4]。葛强[5]运用IDA 方法对连续梁桥进行了易损性分析,表明:桥墩发生中度破坏时,构件更容易完全破坏。毛穗丰等人[6]采用基于IDA 的频数分析法,对连续刚构桥进行了易损性分析,发现边墩较主墩更容易破坏。目前对连续刚构桥地震损伤状态的研究和应用还处于发展阶段,IDA方法能以概率方式体现结构抗震性能。因此,本研究拟采用IDA方法,对六跨连续刚构桥进行地震易损性分析,研究不同位置的墩受横、纵2个方向地震波时的响应结果,可为地震作用时桥梁损伤状态评估提供借鉴。
1 桥梁概况
某桥梁的主桥形式为预应力混凝土连续刚构,跨径布置为73 m+4×130 m+73 m 的六跨对称结构,总长为666 m。箱梁断面形状为单箱单室,根部梁高为8.2 m,跨中梁高为2.6 m。主梁材料使用C55混凝土,纵向预应力筋使用Strand1860钢绞线,按照0.75 倍极限应力施加预应力,竖向预应力钢筋使用螺纹钢棒施加预应力。
桥墩采用钢筋混凝土双薄壁空心墩,单壁平面尺寸为8.5 m×3 m,如图1 所示。双壁外侧距离为12 m,采用C50 混凝土。承台高为5 m,基础采用钻孔灌注桩。汽车荷载标准为公路I 级,地震动峰值加速度为0.3g,地震烈度为Ⅷ度。
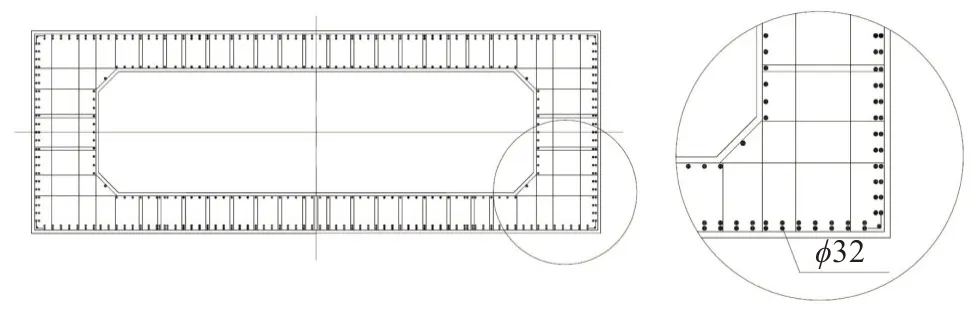
图1 双肢薄壁墩截面钢筋(单位:mm)Fig.1 Reinforcement drawing of double limb thin-walled pier section(unit:mm)
2 损伤指标确定及模型构建
2.1 模型构建
采用Midas Civil 有限元计算软件建立模型如图2所示。薄壁墩从左至右依次编号1#~5#。主梁、桥墩、承台和基础在软件中采用梁单元模拟,采用在两端节点之间设置一个刚度较大的单元,且将该单元自重设为零的方法,模拟墩与主梁固结,过渡墩处采用相应刚度来模拟板式橡胶支座,桩单元通过建立等效土弹簧进行模拟。

图2 有限元模型Fig.2 Finite element model
2.2 IDA法
IDA法是将一条地震波通过放大系数转化为多条波,每条地震波之间相互独立,对其进行非线性时程分析,得到不同地面峰值加速度的结构地震响应结果。整理该结果,得到地震动强度参数和结构性能参数的曲线,称之为IDA 曲线。利用该曲线预测地震强度逐渐增加情况下结构发生弹性或塑性变化的特性。
4 条天然波和3 条人工波见表1,导入桥梁模型进行模拟分析,计算横向地震波冲击影响时应乘以0.85的折减系数[7],其中,PGA 为最大峰值加速度。
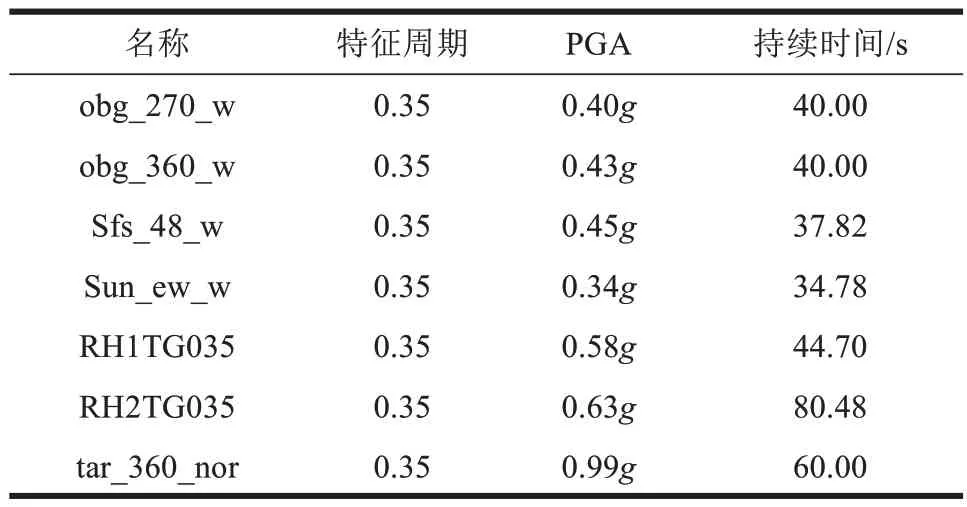
表1 地震波信息Table 1 Seismic wave information
2.3 损伤指标确定
地震作用下,桥梁结构的损伤主要来源于桥墩塑性铰的过大和转动角度桥墩过大的相对位移。因此,研究易损性时,通常以墩柱的延性划分桥梁的损伤程度。用位移延性比作为桥墩地震损伤的指标,其范围见表2。
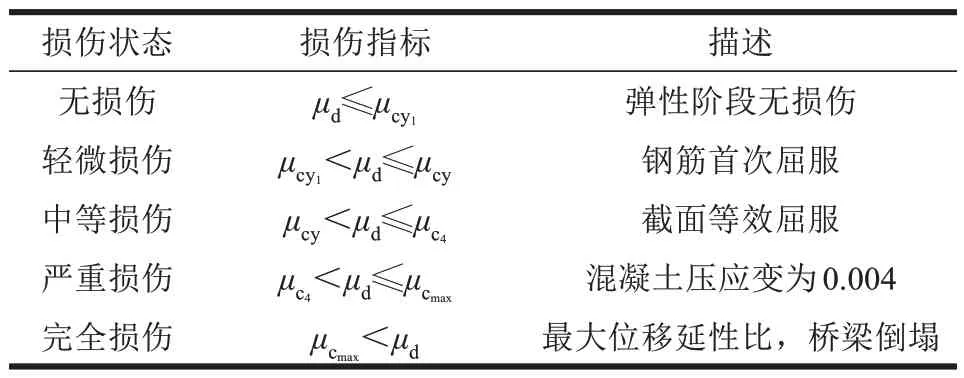
表2 桥墩损伤指标Table 2 Pier damage index
并可根据(1)~(5)进行计算[8]:
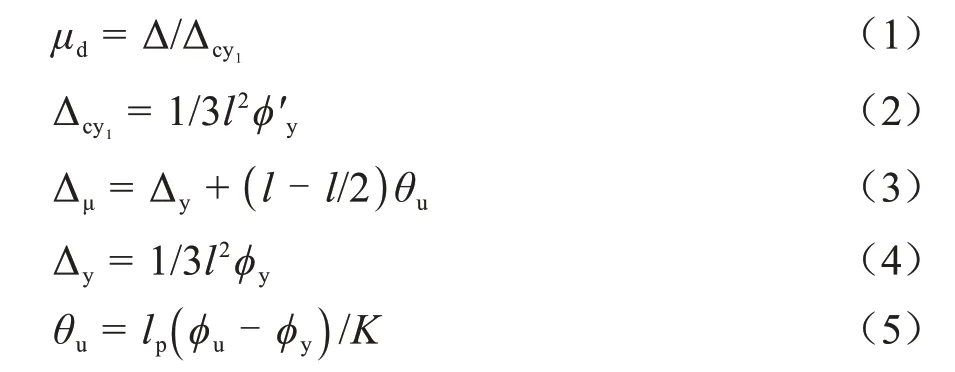
式中:μd为位移延性比;Δ为墩顶最大位移;Δcy1为桥墩纵筋第一次达到屈服时墩顶部的位移;l为墩身高度;ϕ′y为首次屈服曲率;Δu为桥墩出现塑性铰后墩顶总位移;θu为墩底出现塑性铰以后墩顶的塑性转角;Δy墩顶弹性位移;ϕy为等效屈服曲率ϕu为极限曲率;K为安全系数,取值为2;lp为等效塑性铰长度。
lp的计算公式根据《公路桥梁抗震规范》(JTG/T 2231-01—2020)的规定为:
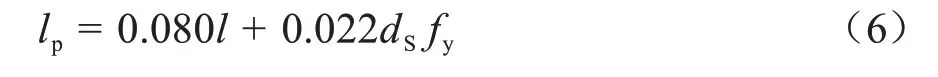
式中:ds为纵筋的直径;fy为纵筋的屈服应力。
通过Midas Civil 计算桥梁各墩轴力,对墩顶截面进行弯矩-曲率分析,其各墩在横桥向和纵桥向的曲率见表3。依据弯矩-曲率值,计算得到各墩损伤位移比,见表4。
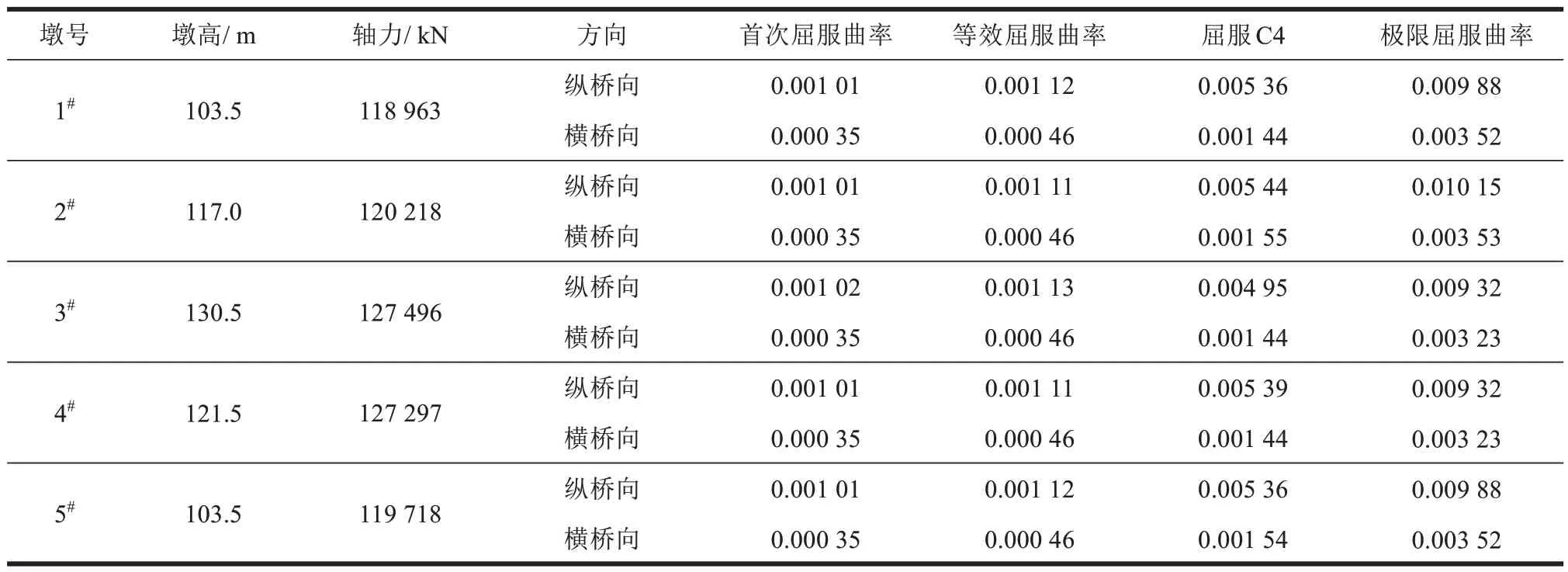
表3 各墩数据及在横纵桥向的各曲率值Table 3 Data of pier and curvature values in transverse and longitudinal direction
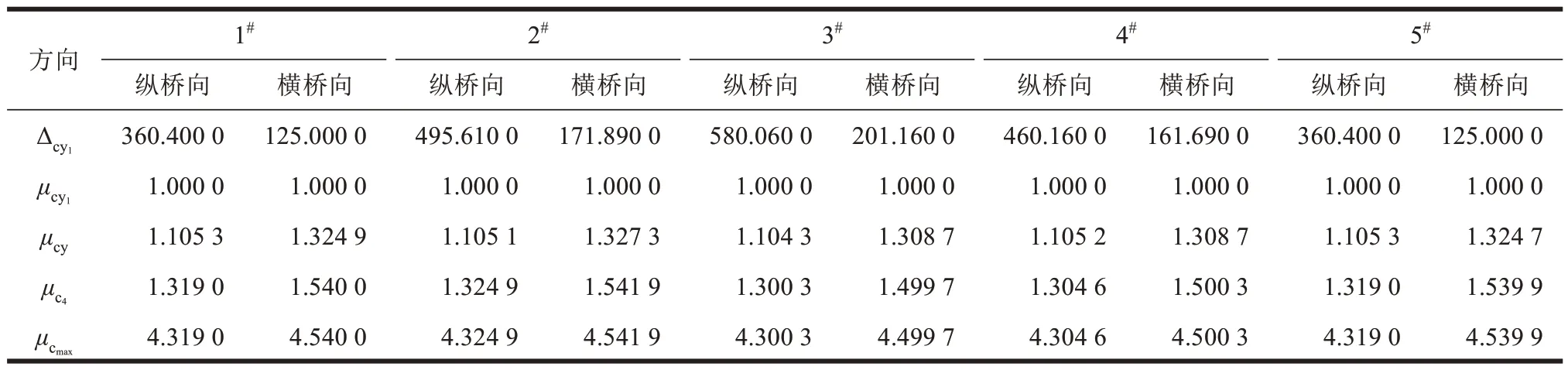
表4 各墩在横纵桥向的损伤指标Table 4 The damage index of pier in transverse and longitudinal direction
不考虑移动荷载效应,以弯矩-曲率曲线为基础,通过计算确定多跨连续刚构桥在不同状态下的损伤指标[10]。以位移延性比为基础,使用IDA方法计算各墩的位移延性比,对各墩的地震需求指标进行回归分析。再带入各状态下的损伤指标,得到各墩的易损性概率,将其与PDA 进行拟合,得到易损性曲线。
3 顺桥向桥墩地震易损性分析
先对所选波进行调幅,再采用IDA 方法进行非线性时程分析,对结构实际的承载能力和桥梁的地震需求取对数值,其值符合正态分布[11]。以PGA(地震动峰值加速度0~1 逐步增加)值的对数值作为横轴,以桥墩顺桥向墩顶截面曲率延性比的对数值作为纵轴,通过最小二乘法对非线性时程分析的数据结果进行线性回归,如图3~7所示。
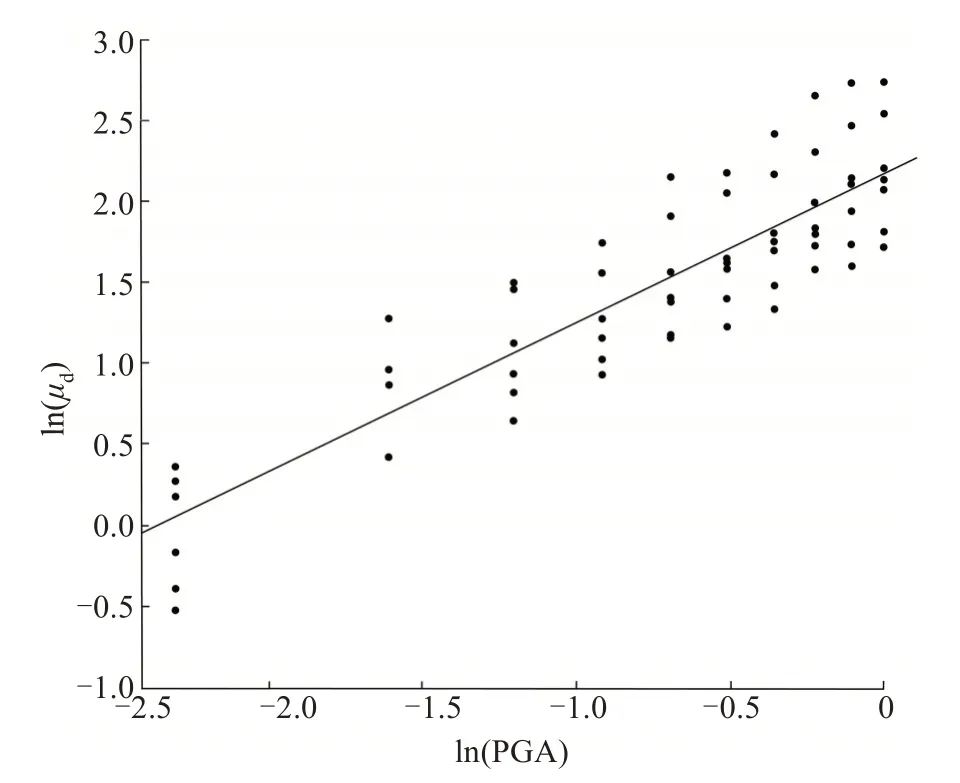
图3 顺桥向1#墩地震需求响应回归分析Fig.3 Regression analysis of seismic demand response of the 1#pier along bridge direction
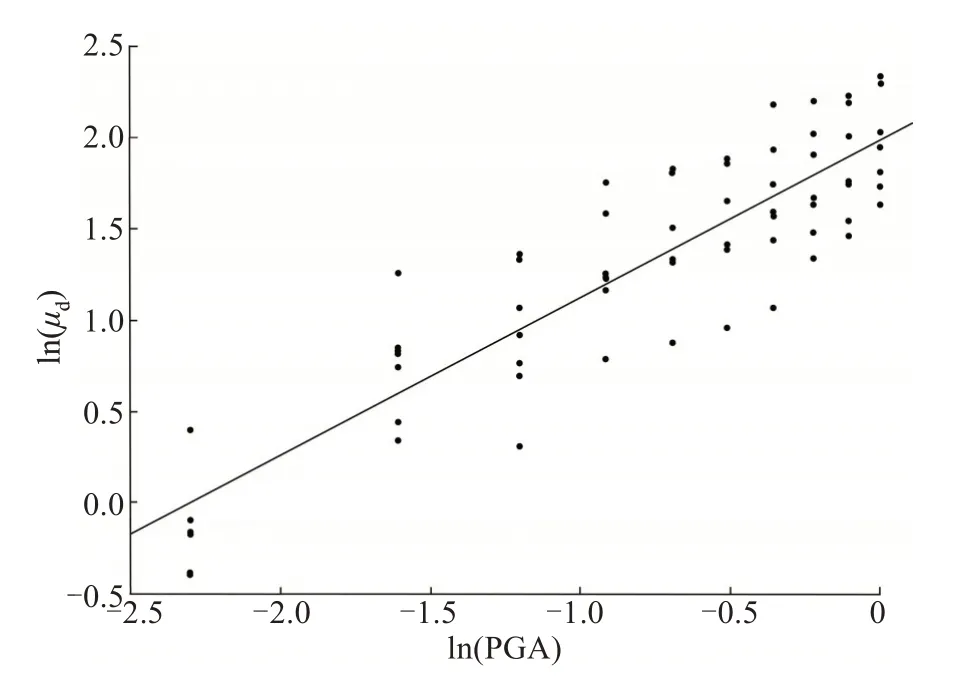
图4 顺桥向2#墩地震需求响应回归分析Fig.4 Regression analysis of seismic demand response of 2#pier along bridge direction
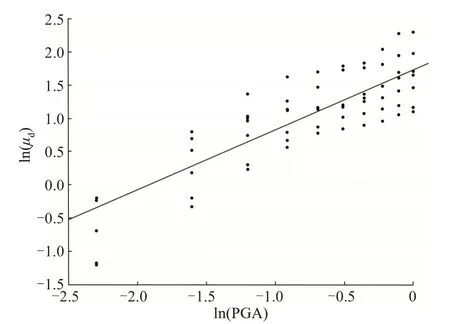
图5 顺桥向3#墩地震需求响应回归分析Fig.5 Regression analysis of seismic demand response of the 3#pier along bridge direction
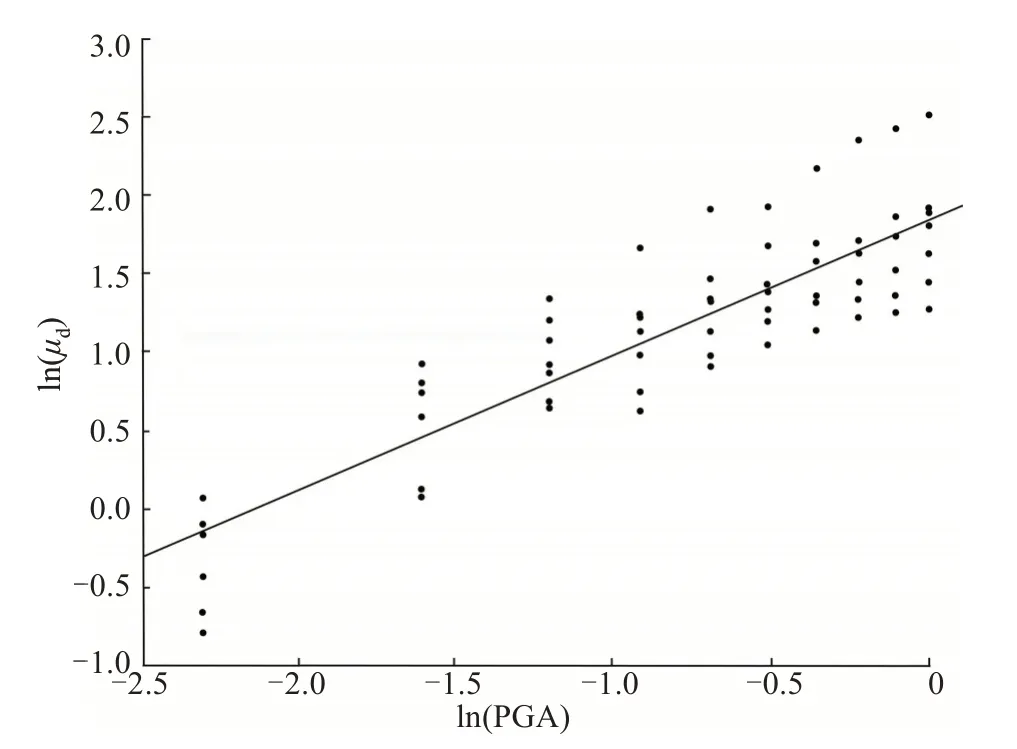
图6 顺桥向4#墩地震需求响应回归分析Fig.6 Regression analysis of seismic demand response of the 4#pier along bridge direction
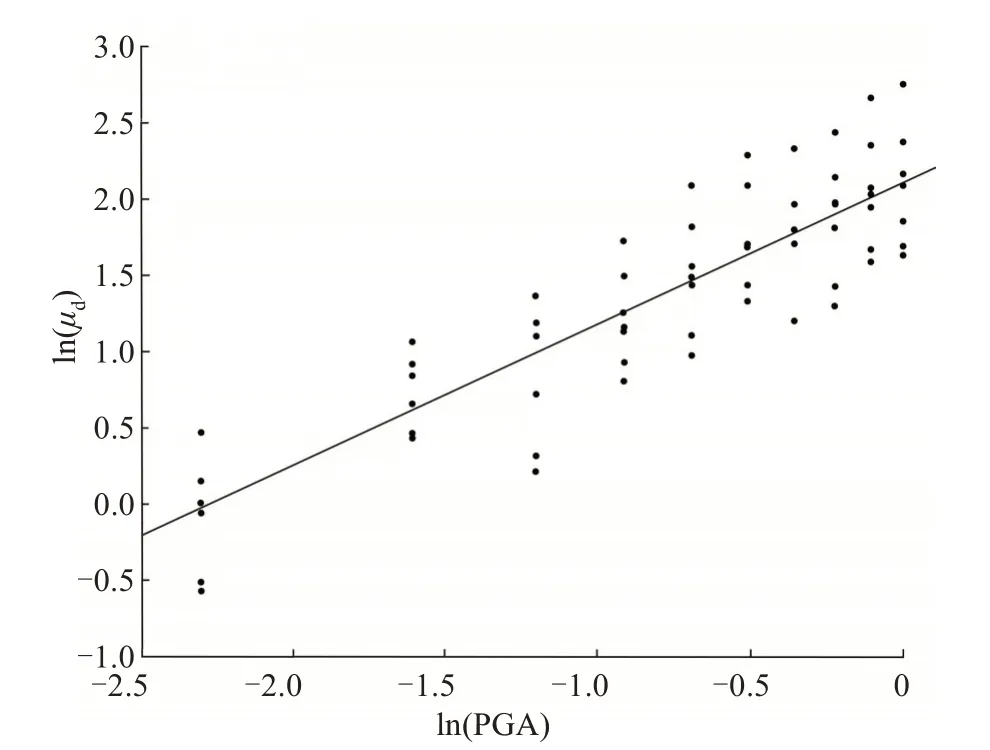
图7 顺桥向5#墩地震需求响应回归分析Fig.7 Regression analysis of seismic demand response of the 5#pier along bridge direction
从图3~7可以看出,5个墩的拟合曲线趋于线性变化,离散程度较小。整理后,可得顺桥向地震作用下桥墩结构位移延性比与地震动强度PGA的函数关系式,见表5,4 种状态的易损性概率见表6。

表5 顺桥向各墩位移延性比与地峰值加速度函数关系Table 5 Relationship between displacement ductility ratio of piers along bridge direction and ground peak acceleration function
先将表5 中各墩的函数关系和表3 的各参数值带入表6计算,得到顺桥向的易损性概率。
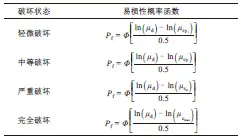
表6 顺桥向各墩在4种状态的易损性概率Table 6 Fragility function of piers along the bridge in four states
根据表6中的公式,进行函数图像拟合,得出各墩的损伤超越概率与PGA的关系曲线,如图8~12所示。
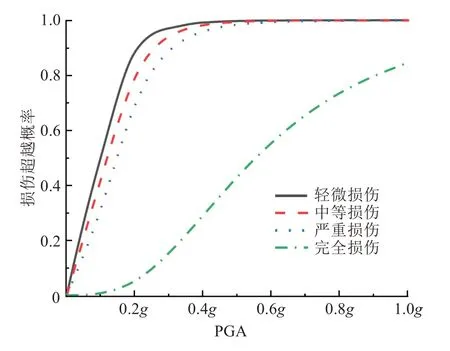
图8 顺桥向1#墩易损性曲线Fig.8 Fragility curve of the 1#pier along bridge direction
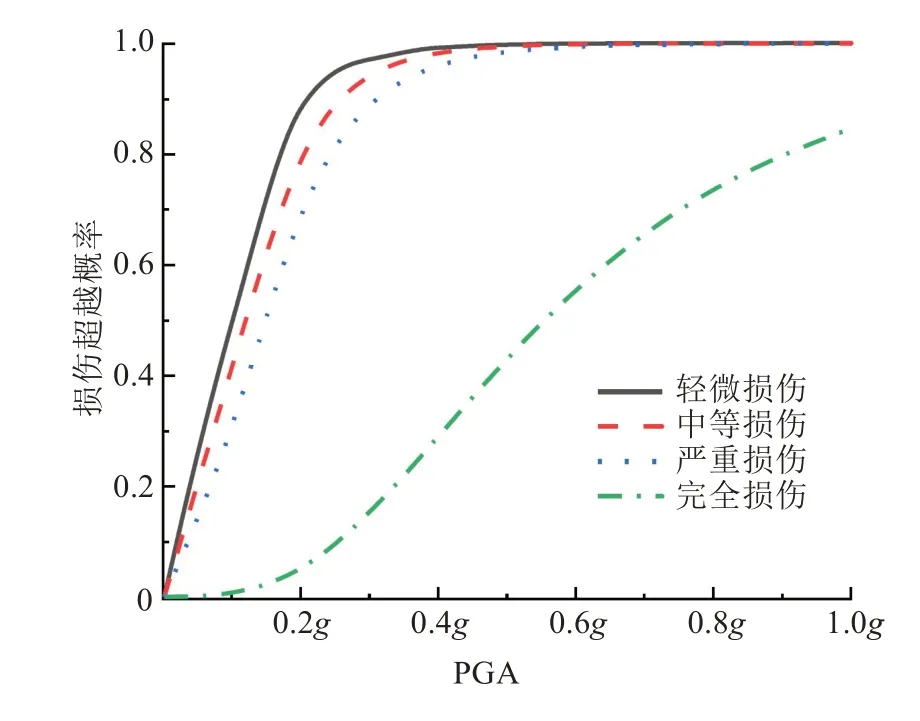
图9 顺桥向2#墩易损性曲线Fig.9 Fragility curve of the 2#pier along bridge direction
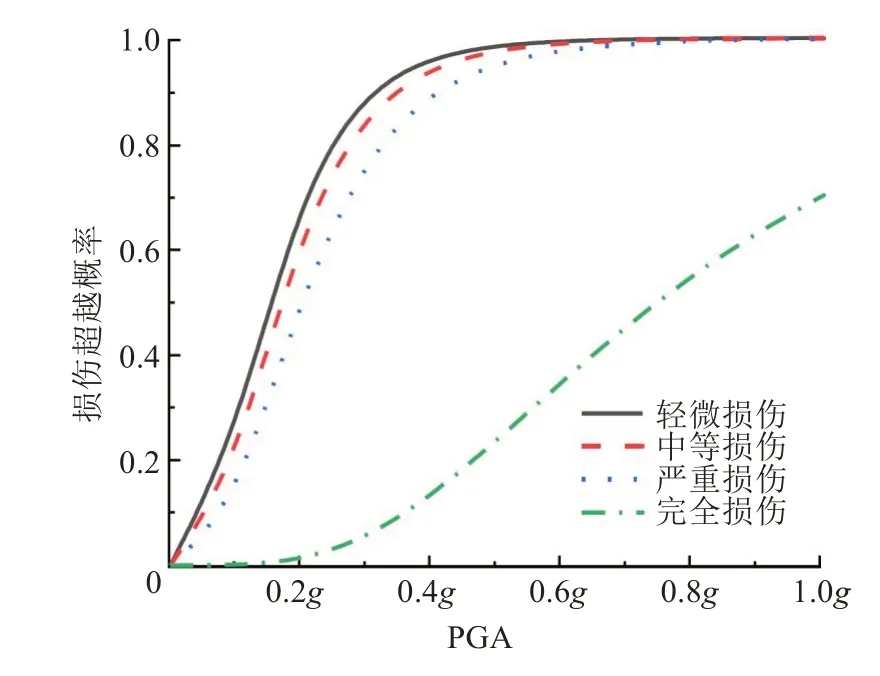
图10 顺桥向3#墩易损性曲线Fig.10 Fragility curve of the 3#pier along bridge direction
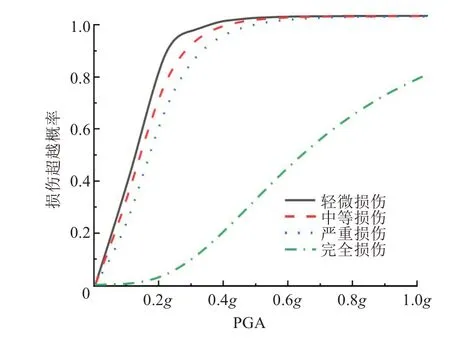
图11 顺桥向4#墩易损性曲线Fig.11 Fragility curve of the 4#pier along bridge direction
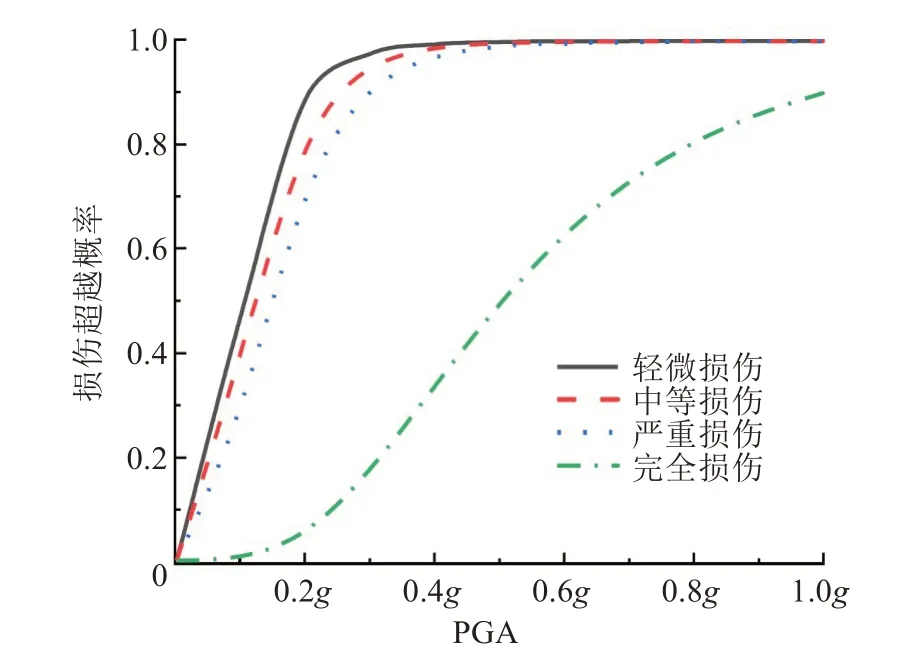
图12 顺桥向5#墩易损性曲线Fig.12 Fragility curve of the 5#pier along bridge direction
损伤概率达到99.9%视为桥墩达到损伤阶段。从图8~12可以看出,多跨连续刚构桥在顺桥向地震作用下,1#~5#墩达到轻微损伤时的地面峰值加速度分别为0.6g、0.7g、0.9g、0.8g、0.6g;达到中等损伤时的地面峰值加速度分别为0.6g、0.7g、1.0g、0.8g、0.7g;达到严重损伤时,1#、2#墩的地面峰值加速度分别为0.7g、0.9g,3#墩在PGA 为1.0g时严重损伤概率为99.83%;未达到严重损伤时,4#、5#墩在PGA 为1g和0.9g时,达到严重损伤标准。完全损伤状态下,在1.0g时1#~5#墩的破坏概率分别为92.40%、84.58%、70.18%、78.30%和89.99%。
从图8~12 还可以看出,顺桥向地震作用时,1#、5#墩的易损性曲线较为接近,2#、4#墩的易损性曲线较为接近,3#墩出现损伤的概率相对最小。宋帅等人[12]研究发现随着刚构桥墩高增加抗震性能随之增加,桥梁中墩较边墩更易损坏。表明:1#、5#墩对称布置,墩高相同,损伤概率接近。2#、4#墩虽对称布置,但4#墩比2#墩高。因此,4#墩受到顺桥向地震作用时,其损伤概率比2#墩的低。在常见地形设计中,中墩桥墩墩高一般较两侧高,可消除中墩更易损坏的缺陷。
4 横桥向桥墩地震易损性分析
采用IDA 的方法,可以得出横桥向地震作用时各墩的损伤超越概率与地震动峰值加速度PGA的关系曲线,如图13~17所示。
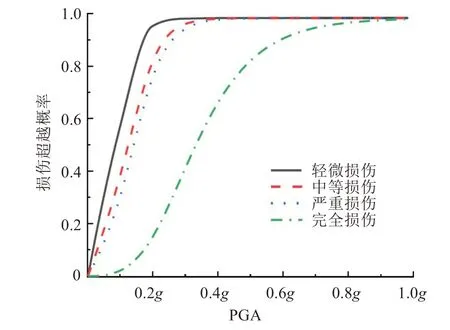
图13 横桥向1#墩易损性曲线Fig.13 Fragility curve of the 1#pier in transverse direction
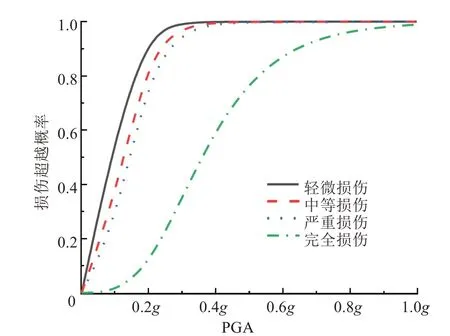
图14 横桥向2#墩易损性曲线Fig.14 Fragility curve of the 2#pier in transverse direction

图15 横桥向3#墩易损性曲线Fig.15 Fragility curve of the 3#pier in transverse direction
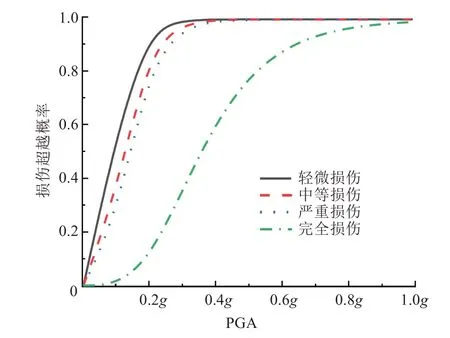
图16 横桥向4#墩易损性曲线Fig.16 Fragility curve of the 4#pier in transverse direction
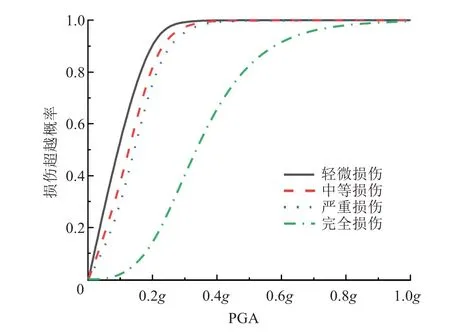
图17 横桥向5#墩易损性曲线Fig.17 Fragility curve of the 5#pier in transverse direction
同样将损伤概率达到99.9%视为桥墩已到达损伤阶段。从图13~17 可以看出,多跨连续刚构桥梁在横桥向地震作用,1#~5#墩达到轻微损伤时,地面峰值加速度分别为0.4g、0.4g、0.5g、0.4g、0.4g;达到中等损伤时的地面峰值加速度分别0.5g、0.5g、0.6g、0.5g、0.5g;达到严重损伤时的地面峰值加速度分别为0.5g、0.6g、0.7g、0.6g、0.5g。在完全损伤状态下,PGA 在1.0g时,1#~5#墩的破坏概率分别为99.56%、99.02%、97.68%、98.93%、99.58%。
从图13~17 还可以看出,轻微损伤、中等损伤、严重损伤各状态下的易损性曲线在0.5g之前几乎呈线性变化,且损伤概率上升较快。这是由于桥梁还处于弹性阶段,主要由钢筋承受应力,完全损伤状态下的易损性曲线呈非线性变化,且各损伤状况与受到顺桥向地震作用时不同。因此,墩高对对称布置墩的损伤概率影响不大。
5 全桥易损性分析
桥梁任何一个构件的破坏都可能造成全桥的整体破坏。全桥的易损性分析是一种直观、科学、系统的比较方法。采用一阶界限法对该桥进行全桥的易损性分析[13],相比其他方法,这种方法更保守,更简便。通过将每个构件进行串联,构成了一个桥梁系统。地震作用下,只要桥梁系统的任一构件损伤概率达到指定的损伤状态,则认为桥梁达到了对应的损伤状态。其计算式为:
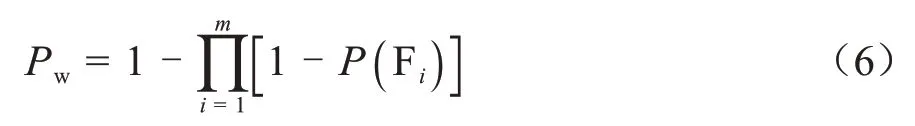
式中:Pw为桥梁达到指定损伤状态的概率;P(Fi)为第i个构件达到指定损伤的概率。
根据式8计算各构件各损伤状态的概率,并得到全桥的易损性曲线,如图18~19所示。
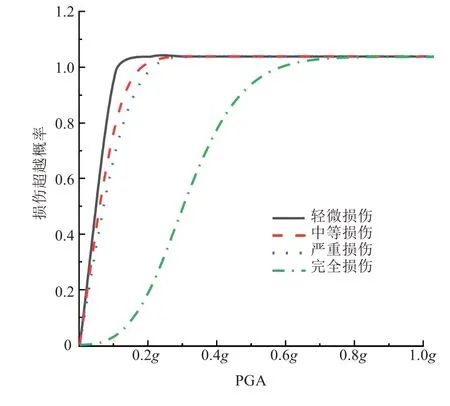
图18 顺桥向全桥易损性曲线Fig.18 Fragility curve of the whole bridge along the bridge
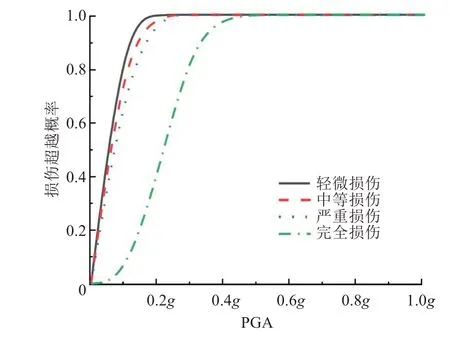
图19 横桥向全桥易损性曲线Fig.19 Fragility curve of the whole bridge in transverse direction
从图18~19 可以看出,完全损伤的易损性曲线较为平滑,轻微损伤、中等损伤与严重损伤曲线较为接近。表明:地震作用下,混凝土开裂的速度较快,塑性铰的出现也较快。其中,横桥向相对于顺桥向,前3 个损伤阶段的变化差距不大,但在完全损伤阶段,横桥向的损伤发展较快,多跨连续刚构桥在横桥向更易坍塌。
全桥的易损性曲线呈两阶段变化规律:①轻微损伤、中等损伤与严重损伤时,全桥易损性曲线呈近似于线性的变化规律。在0~0.2g的地震动峰值加速度区间内,桥梁系统损伤概率急剧上升。在0.3g时,各项损伤概率都达到了100%。②完全损伤概率变化趋于非线性,这是由于桥梁结构呈非线性变化,桥梁为塑性变化阶段,塑性铰大量出现。因此,桥梁结构主筋已进入屈服阶段,桥梁趋于坍塌。在0.5g时,完全损伤概率已达到99.946 6%。在0.7g时,完全损伤概率达到了100%。
6 结语
以一座多跨连续刚构桥为工程背景,采用IDA法,以位移延性比作为地震损伤指标,对桥梁5个双肢薄壁墩进行易损性分析,得出结论为:
1)多跨连续刚构桥桥墩呈对称布置。位置对应、墩高相同的墩的地震易损性基本一致。当受到顺桥向地震作用时,对称位布置的墩越高,达到相同损伤状态的概率越低,而当受到横桥向地震作用时区别不明显。
2)连续刚构桥各桥墩在受到横桥向地震作用时的损伤概率相较于顺桥向地震作用时的损伤概率更高。
3)同一多跨连续钢构桥中,墩高越高,损伤概率越低。常见地形设计中,中间桥墩墩高一般较两侧边墩高,能使中墩更牢固。
4)刚构桥全桥达到轻微损伤、中等损伤和严重损伤时,曲线较为接近,且发展较快,易达到损伤指标,完全损伤曲线呈非线性,前段和后段发展较缓,中段发展较快。受到横向地震作用时比受纵向地震波作用时更容易被破坏。

