风屏障对桥梁及列车的气动特性影响研究

董国朝，黄佳颖，韩艳

（长沙理工大学 土木工程学院，湖南 长沙 410114）

随着基础建设的快速发展，交通运输体系外扩[1]，中国规划建设的大型运输铁路网覆盖了各种强风场地区。在高速铁路上建设桥梁，可提高空间利用率，降低混行风险，优化建设布局，增大建筑空间，但广泛应用会大幅度提高列车行驶高程，降低桥上列车行驶的安全性。为保证高速列车在铁路桥梁上的行车安全性，通常考虑设置风屏障来降低风速[2]，但风屏障的存在增大了桥梁的挡风面积，对车桥系统的流场产生了干扰，影响了整体的抗风设计[3]。因此，考虑在桥梁上加装风屏障时，应设置合理的风屏障高度和透风率，以达到最优效果。目前，国内外针对风屏障高度和透风率的设置研究主要是数值模拟和风洞试验。TELENTA 等人[4]通过试验和数值模拟方法，研究了风屏障挡风角度调整与不同湍流流动的机理，但仅考虑了风屏障对桥梁的影响。LEE 等人[5]讨论了风屏障的设计准则，在侧风作用下如何提高高速公路运行车辆安全性的方法。施成华等人[6]通过建立三维风-车-桥模型，进行了动态数值模拟。通过设置桥梁风屏障后，对列车驶入隧道过程中的行车安全性和气动性能进行研究。刘叶等人[7]对侧风作用下的平层公铁桥梁-列车-风屏障系统气动特性进行了风洞试验研究，针对风屏障不同的透风率和高度，对不同偏角下桥上中间列车的三分力系数进行了测定，研究了风屏障参数问题。周蕾等人[3]利用计算流体动力学（computational fluid dynamics，简称为CFD）进行了数值模拟和风洞试验，从风屏障的结构选型和高度等角度讨论了对车桥系统气动性能的影响，但未考虑列车头的流线型特征，未能较好地得到实际流场分布，其数值模拟的精度也不够准确。这些研究成果均表明：风屏障提高了铁路桥梁上列车行车安全性与舒适性。但针对风屏障高度、透风率等对列车不同部位影响的研究较少，从车桥整体气动性能优化的角度，得到最佳风屏障参数取值的研究更为鲜见。因此，本研究拟通过数值模拟和风洞试验方法，对侧风下平层公铁两用桥梁的车-桥-风屏障系统气动性能进行研究。通过对不同的风屏障高度和透风率进行数值模拟，探究风屏障参数对实际桥梁动力特性的影响，并与风洞试验结果进行比较，验证模型的准确性，再通过数据包络分析（data envelopment analysis，简称为DEA）计算不同风屏障参数下对应的车桥整体相对效率值，给出该类车桥下风屏障参数的最佳取值，为实际工程提供借鉴。

1 数值模拟参数设置

1.1 模型参数

对某平层公铁两用大桥和高速列车进行了多工况的风洞试验，为确保准确性，数值模拟中保留公路与铁路之间设置的防护栏。数值模拟中，车桥模型与风洞试验中均采用1∶43 的几何缩尺比。考虑到风洞试验布置和数值模拟中网格划分的可行性，对试验模型进行了部分简化，去除了列车原型的列车轮对、转向架和受电弓等列车细部构造，同时忽略了桥梁上检修轨道、拉索等附属设施。

缩尺后的列车模型尺寸为长1 775.8 mm×宽78.6 mm×高81.4 mm，其三维模型如图1 所示。列车的流线型车头对车桥系统的流场影响不可忽略。因此，在风洞试验和数值模拟中，完整保留头车和尾车的几何外形。列车采用头车、中车和尾车3节列车模拟等效整个列车。外形相对比较规则的中间车辆，这种模型气动性较为稳定，能较好地反映整个中间车节。

图1 列车简化模型（单位：mm）Fig.1 Simplified model of train(unit:mm)

简化后的桥梁保留了对整体气动特性影响较大的桥上栏杆，设置列车底部与桥梁顶面距离为0.5 m 来等效轮对高度。车桥整体三维模型如图2所示。

图2 公铁两用桥梁模型Fig.2 The mode of combined highway and railway bridge

采用等效透风率法对风屏障进行等效处理[4-7]。采用多块单板组成风屏障，如图3 所示。其中，s为风屏障条的间隙，h为单个风屏障条的高度。风屏障高度（H）定义为最顶部单板顶面距离桥面的高度，单板之间的距离（S）相等，透风率β=5S/H×100%。

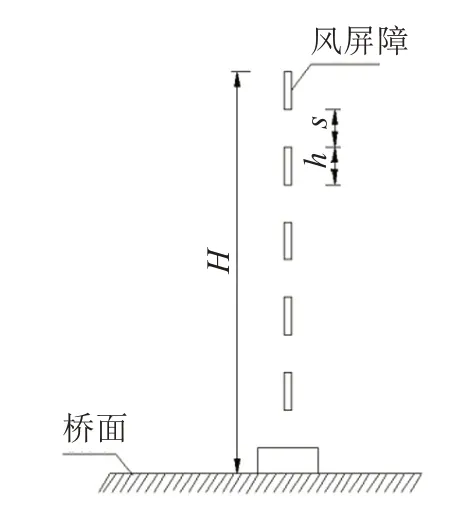
图3 风屏障等效模型Fig.3 Equivalent model of wind barrier

1.2 工况设置

为研究不同风屏障高度和透风率对车桥系统气动性能的影响，本试验分别对风屏障高度为0、2.0、3.0、3.5 和4.0 m，透风率为20%、40%和60%的13 种不同工况进行数值模拟，测定对应的三分力系数。

2 数值方法和网格划分

根据实际流场性质，采用三维、非定常、不可压缩和黏性流场对风屏障作用下的车桥系统进行数值模拟。

由于本研究的计算对象是车桥，重点考虑逆压梯度分离引起的力的变化。因此，选用考虑了逆压梯度分离的SST k-w 模型。考虑到SST k-w 湍流模型对近壁面区域网格细化的要求[8]，一般控制Yplus值在1左右，确保达到湍流应用条件。

几何模型的网格在ICEM CFD 中进行，考虑计算资源和精度，本试验对整体结构采用全结构六面体进行网格划分，而不采用精度差的混合网格划分方法，对列车流线型车头进行细化分块，确保复杂表面网格的质量。考虑到高速列车的车身表面复杂性，将整个计算域分为高速列车区域和桥梁-风障区域，以方便对2 个区域采用不同的切块形式，对列车车身周围网格进行了内外O 型切分，实现网格贴体和更好的网格尺寸过渡，能对近壁面的第一层网格高度进行控制，满足网格中Yplus值要求。

选用全结构化网格的另一个优势是可更好地控制网格质量，列车及桥梁-风屏障部分网格如图4 所示。高速列车区域的网格（80.96 万）质量最小值为0.710，桥梁风障区域的网格（481.80 万）质量最小值为0.941，确保了数值模拟的准确度。

图4 全结构网格划分示意Fig.4 Signal of full structure grid

计算域的设置直接影响数值模拟结果的准确性，为确保数值模拟准确性与计算效率，采用的计算域如图5所示。由于不考虑风偏角对车桥系统的影响，本数值模拟采用单进风口，设置迎风侧流场边界为速度入口，背风侧流场边界为压力出口，设置桥梁两端为对称边界，其余均设置为壁面边界。

图5 计算域示意（单位：m）Fig.5 Schematic diagram of computational domain(unit:m)

3 风洞试验验证

为验证数值模拟的准确性，风洞试验和数值模拟选用的桥梁节段和列车模型尺寸一致，均保持与原车桥1∶43的缩尺比，在长沙理工大学的风洞高速试验段进行模型试验。本试验模拟中采用的风速为10.6 m/s 的均匀来流，湍流强度控制在0.5%以内。

模型为某平层公铁两用大桥，桥梁中间为双线铁路，线间距为4.6 m，铁路两边是双向6 车道的高速公路，公路与铁路之间设防护栏。主梁断面如图6 所示，桥梁三分力通过测力天平得到数据。

图6 主梁断面Fig.6 The main beam section

列车原型为CRH2型客车，列车模型尺寸为长2 300 mm×宽78.6 mm×高81.4 mm。在横风条件下，考虑列车风对桥梁和风屏障的影响，为更好地捕捉头车和尾车的复杂流场，保留车头部分完整的细部特征，确保与数值模拟的一致性。列车测压断面和测压孔布置如图7所示，采用扫描阀连接进行数据采集。

图7 列车测压孔位布置Fig.7 Layout of holes for train pressure measuring

风洞试验中，采用等效透风率法，选择2.75 m高、40%透风率作为试验的风屏障参数取值。考虑到不同风攻角对应的三分力系数呈现不同变化趋势，试验中，通过转动底部转盘实现不同的风攻角，从而测定－1°、0°和+1°不同风攻角对应的三分力系数。

桥梁采用2台六分量应变天平测量气动力和气动力矩，列车采用原装进口美国PSI DTC Initium电子压力扫描阀，512 个通道自由组合供选用（64通道/块×8 块），各压力测量通道精度为0.06%；参考点的风速由皮托管测量得到。试验中采样时长为30 s，采样频率为330 Hz。

数值模拟的三分力系数与风洞试验结果对比如图8所示。其中，扭矩系数随风攻角变化的趋势与试验监测基本一致，但由于升力矩系数在小攻角下数值较小，因此该误差相对较大。试验测定的列车头部阻力系数和升力系数与数值模拟基本吻合，最大误差仅为8.86%（0°攻角下的列车阻力系数），试验结果表明：对车桥三分力的网格划分和数值计算是可行的。

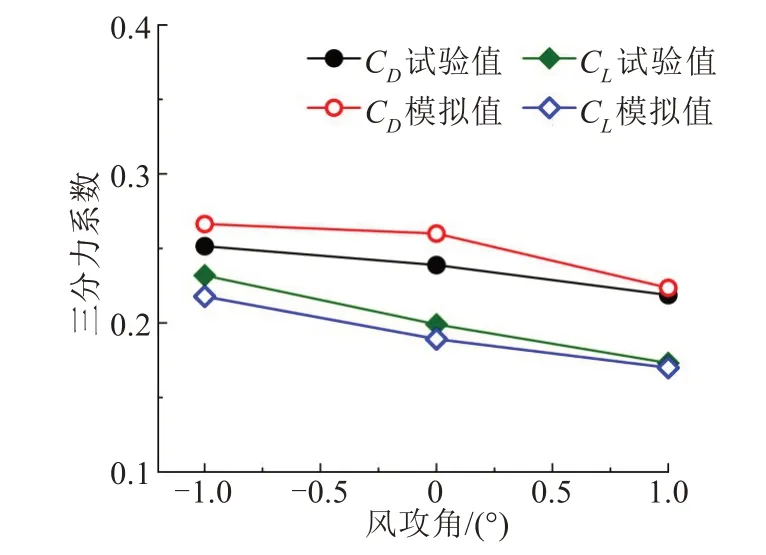
图8 三分力系数结果Fig.8 Three component coefficient results

4 数值模拟结果分析

4.1 风屏障透风率和高度对桥梁气动性能的影响

不同风屏障高度和透风率下桥梁的三分力系数变化规律如图9所示。

从图9 中可以看出，随着风屏障高度的增加，风屏障增大了桥梁的挡风面积，桥梁的阻力系数一直上升。考察各分段之间的斜率，发现桥梁阻力随风屏障高度增大呈先逐渐快速增加后放缓，特别是在风屏障高度为3.0～3.5 m 时，阻力系数上升较为平缓，随后在3.5～4.0 m 时上升趋势明显加快。透风率对桥梁阻力系数的影响较为直观，风屏障高度相同的情况下，透风率越高，阻力系数越小。

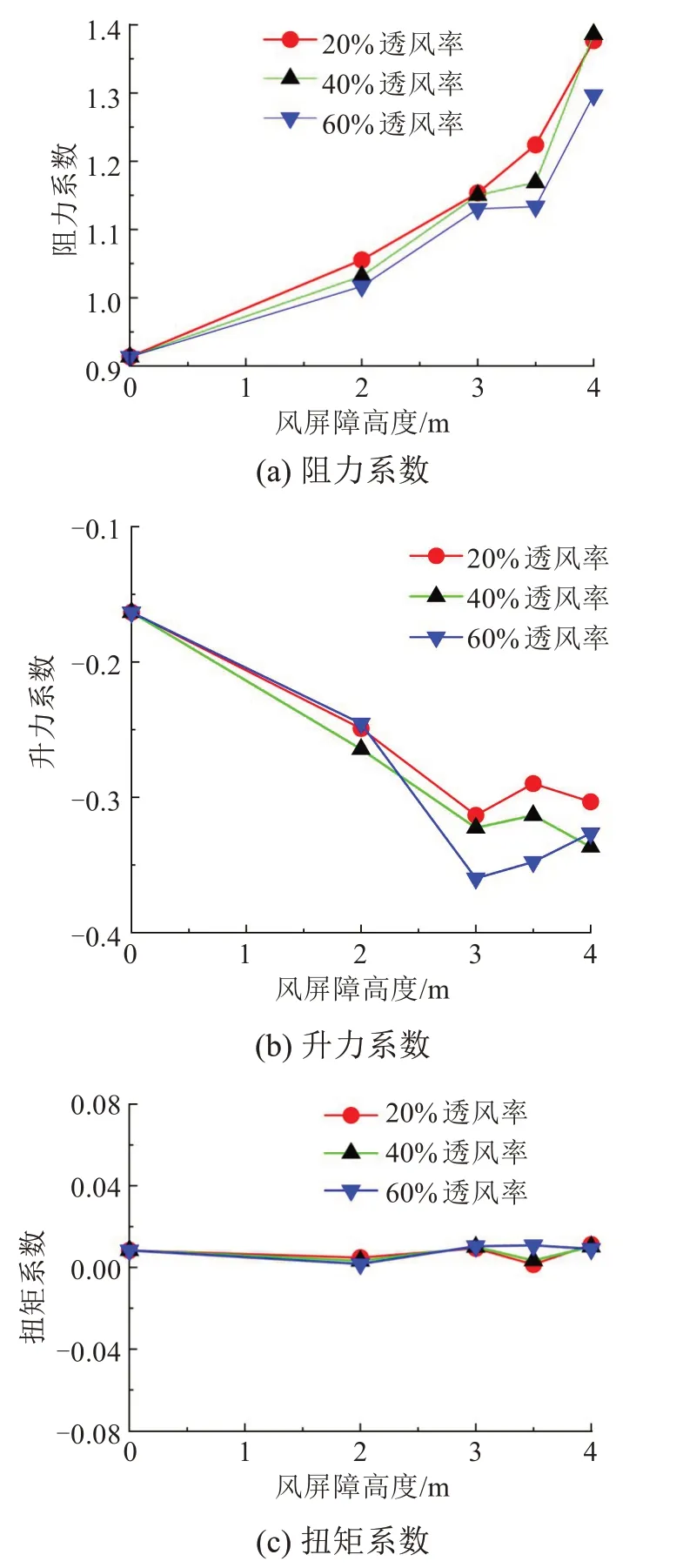
图9 不同风屏障参数下的桥梁三分力系数Fig.9 Three component coefficient of bridge at different wind barrier parameters

桥梁的升力系数在整组工况中为负值，随着风屏障高度的增加，先下降后上升，随后再次下降，在风屏障高度为3.0 m 时取极小值。由于本试验所有工况仅考虑0°攻角下三分力系数的变化，扭矩系数变化趋势不大，在0值附近上下波动。因此，扭矩系数保持在0值附近。其中，在风屏障高度为3.5 m，透风率为20% 时，桥梁的扭矩系数与0差值最小。

4.2 风屏障透风率和高度对列车气动性能的影响

不同风屏障高度和透风率下列车的三分力系数变化规律如图10所示。

从图10 中可以看出，桥面增加了风屏障后，列车的气动性能得到明显改善，阻力系数随风屏障高度升高而下降，3.5 m 之后已无明显变化，这是由于此时的风屏障高度基本与列车高度接近。在60%高透风率下，随着风屏障高度的增加，列车的阻力系数在经历长段下降之后再次上升。这是因为保持较高的透风率，增加风屏障高度，遮蔽效果会变差，导致列车受到更大的横风干扰。升力系数与阻力系数变化趋势类似。表明：高透风率下风屏障的遮蔽效果不明显，扭矩系数随风屏障高度增加逐渐减小；低透风率下风屏障工况会有更好的防风效果，在4.0 m时效果最好。

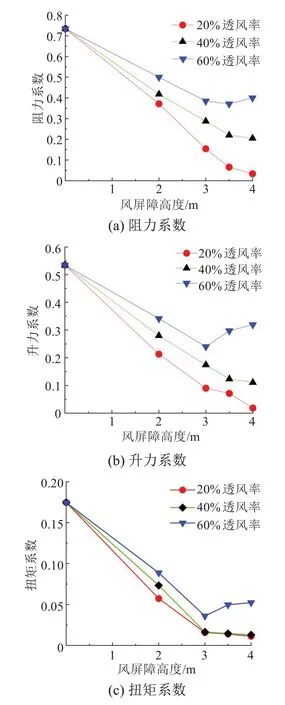
图10 不同风屏障参数下的列车三分力系数Fig.10 Three component coefficients of bridge at different wind barrier parameters

5 风屏障参数优化选型

5.1 DEA评价模型

DEA 算法引入一个相对效率作为参考指标来进行效率评价，主要使用投入、产出指标的决策单元（decision making unit，简称为DMU）对本研究中不同风屏障参数取值进行评价分析。通过数学规划对各种决策单元之间的相对有效性进行评价。由于DEA 方法对多指标决策方案（单元）的评价具有很大优势，被广泛应用到很多领域[9-10]。

假定有n个决策单元，每个决策单元有p种输入和q种输出形式，Xi和Yi为第i个风屏障输入及输出指标向量，决策单元的效率评价指数为：

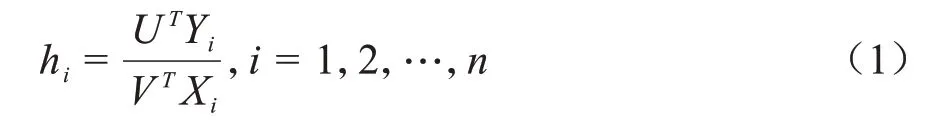
式中：U=(u1，u2，…，uq)T、V=(v1，v2，…，vp)T分别为输出和输入指标对应的权重系数。

对应的最优化模型为：

再经过Charnes-Cooper变换和对偶理论的线性规划变换，可得：

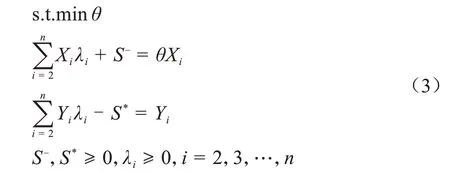
式中：θ为第1 个风屏障的相对效率；λi为变量；S-、S*分别为松弛变量。

在风洞试验中，得到风屏障参数对桥梁和桥上列车的气动性能影响规律。考虑桥梁与列车各自三分力受风屏障参数取值的影响不同，未得到风屏障参数的合理取值。从桥梁设计角度出发，考虑桥梁安全性能与列车安全性能，利用DEA 方法，利用数值模拟得到的数据进行多目标优化评估。

5.2 评估结果分析

使用DEA 评价模型对不同工况下列车与桥梁的三分力系数进行评估，结果见表1～3。

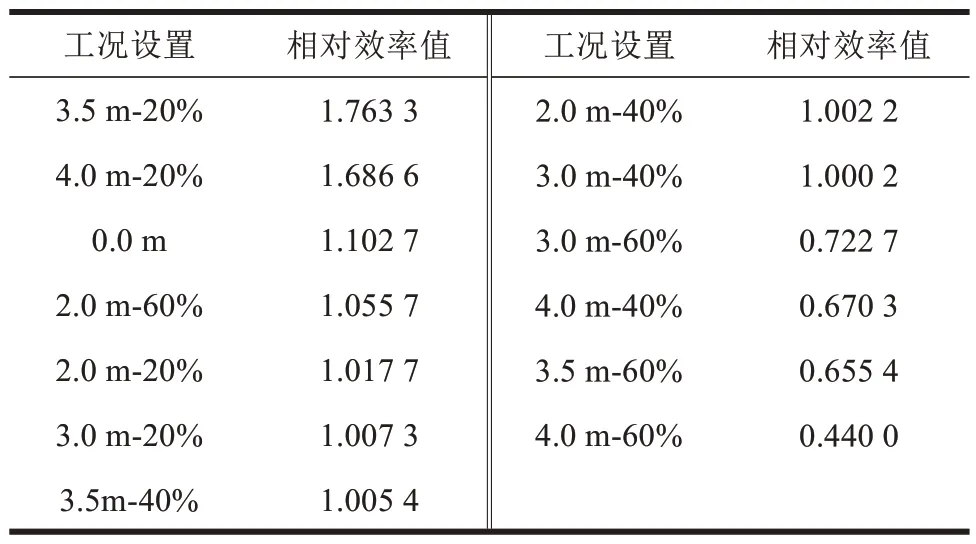
表1 仅考虑桥梁时风屏障参数取值的相对效率Table 1 Relative efficiency of wind barrier parameters under the consideration of bridge

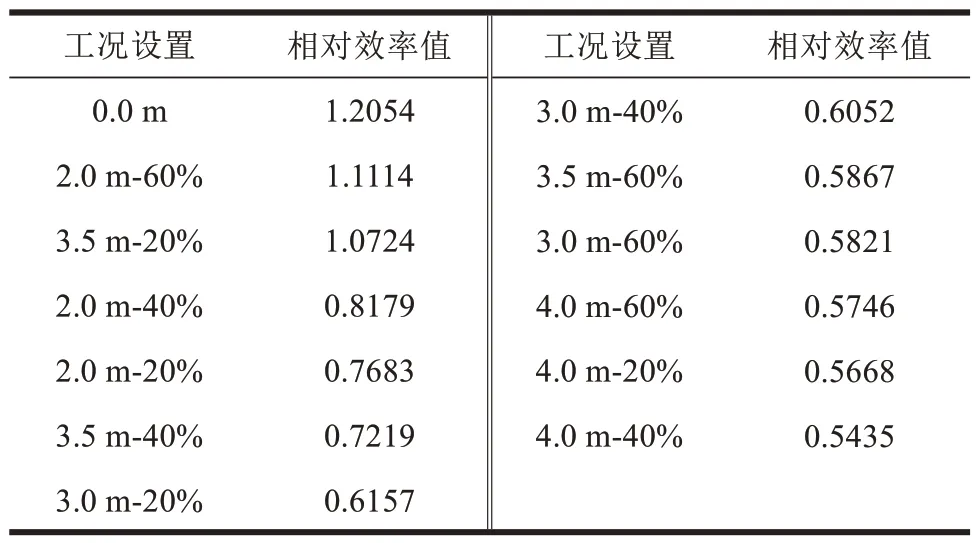
表2 仅考虑列车时风屏障参数取值的相对效率Table 2 Relative efficiency of wind barrier parameters under the consideration of train

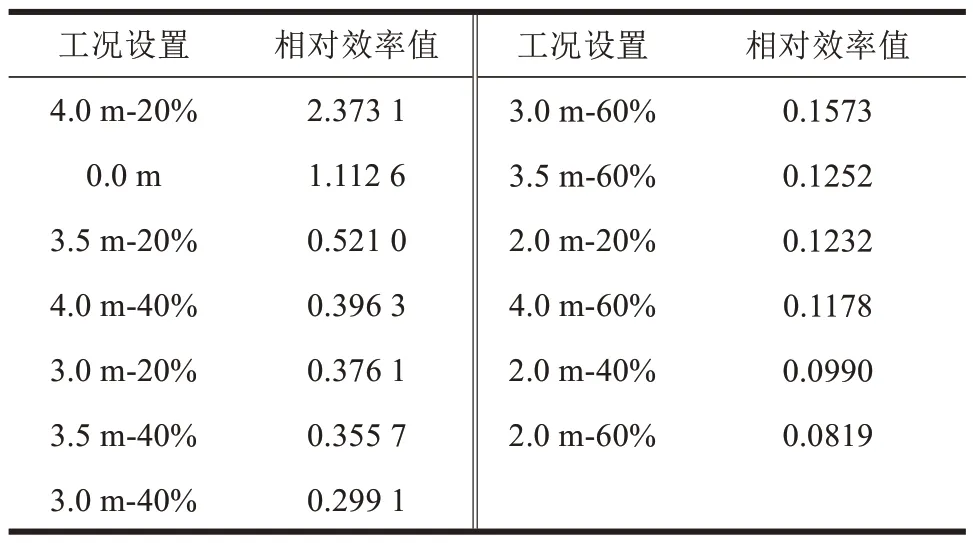
表3 综合考虑列车与桥梁时风屏障参数取值的相对效率Table 3 Relative efficiency of wind barrier parameters under the comprehensive consideration of train and bridge

由表1～3 可知，仅考虑桥梁安全性能时，风屏障参数的最佳取值为0.0 m，即不设置风屏障。仅考虑列车时，风屏障参数中屏障的高度和透风率的最佳取值分别为4.0 m 和20%。考虑车桥系统气动力系数随风屏障参数取值变化的影响，风屏障高度为3.5 m、透风率为20%时，得到相对效率值最大（1.763 3）。多目标评价的结果在单目标评价结果（仅考虑车辆和仅考虑桥梁）之中，验证了多目标评价的合理性。

6 结论

以某公铁两用桥为例，利用CFD 对不同风屏障参数取值的车桥气动三分力进行了数值模拟，并将所得成果与风洞试验结果进行对比，验证了数值模拟的准确性。通过分析风屏障高度和透风率的变化对桥梁和桥上列车气动力的影响规律，得到结论为：

1）风屏障高度升高，透风率减小，挡风面积变大，桥梁的气动力系数逐渐增大。表明：桥梁气动力受风屏障高度比透风率的变化更为敏感，而风屏障的存在为桥上列车提供了遮蔽效果，使桥上列车的气动力系数呈相反的变化趋势。

2）风屏障透风率较大时，即使增加风屏障高度，也达不到较好的防风效果，但仅从单独的三分力进行评估，尚未得到合理的风屏障参数取值。

3）通过DEA算法，分别计算得到单独考虑列车、桥梁和车桥整体气动性能下的风屏障相对效率值。表明：风屏障高度为3.5 m 且透风率为20%时，车桥整体的气动性能最优。