弯桥抗倾覆性能研究

宋恒扬，李海涛

(四川省公路规划勘察设计研究院有限公司，四川 成都 610041)

0 引 言

箱梁结构广泛应用于国内外市政高架、立交枢纽、公路互通匝道等结构。为满足通行要求，桥下空间受限时，常采用独柱式桥墩，减少占地空间。互通匝道桥因受纵坡及线形等条件所限而体现出坡、弯、斜、异形等不同特点，从受力角度上，不仅具有直桥的共性，同时具有自己的特征，相对于直梁桥剪、弯作用，匝道桥在剪、弯、扭等复合作用下进行受力。常规匝道桥面宽度一般取8～15 m，曲率半径取60～225 m之间，大部分为等高或变高预应力混凝土连续箱梁[1]。

通常情况下，匝道桥的两端设置抗扭支座，中间采取点铰支座或固结，或者是点铰和抗扭混合使用。第一种支座方式在城市立交中较为普遍，优点是中间单墩单支座占据空间小，外观简洁优美。第二种支座方式主要结合实际情况，中墩采用抗扭支座，此种设置可大大改善曲线桥梁的受力，但通常占据面积较大，且外形不如单墩单支座简洁。

近年来我国相继发生数起匝道桥倾覆垮塌案例如表1所示，上述事故均具有相同的特征。桥梁两端设置抗扭支座，中间进行点铰支撑；发生事故起因均是偏心荷载作用，支座脱空，支撑体系失效，倾覆事故中，超载现象尤为突出；结构破坏突然，梁体倾覆后，主梁、桥墩基本完好无损，部分支座，盖梁破坏[2]。

表1 倾覆箱梁匝道信息

1 桥梁抗倾覆计算流程

《公路桥涵设计通用规范》(JTG D60—2004)只提及抗倾覆验算，但并未给出详细的计算公式，在《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)中详细给出了计算方法，桥梁倾覆属于承载能力极限状态范畴。梁体从正常状态到倾覆破坏经历了两个过程。在状态1，单向受压支开始脱空，单向支座持续脱空；进入状态2，箱梁抗扭支撑失效，箱梁变形发散、梁体翻转、支座被挤出、桥墩断裂。针对上面两种特征状态，进行两种抗倾覆验算工况验算。

(1)基本组合下，单支座受压。

(2)稳定作用效应/失稳作用效应≥2.5。

2 直、弯桥倾覆受力特性

倾覆始于支座脱空，直桥与弯桥的倾覆差异及弯桥的曲率半径大小对其抗倾覆性能的影响[3-4]，同时温度作用对弯桥的横向移动的影响都是需要研究的问题。通过对比同跨径直桥和弯桥的抗倾覆性能，同时对比不同曲率半径的弯桥抗倾覆性能及弯桥在温度荷载作用下的横向爬移得出相关结论。

直桥和弯桥的支座布置形式如图1和图2，两边设置抗扭支座，中间设置单支座。

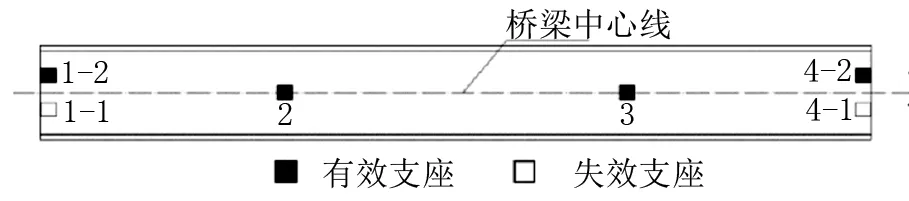
图1 直线桥支座布置

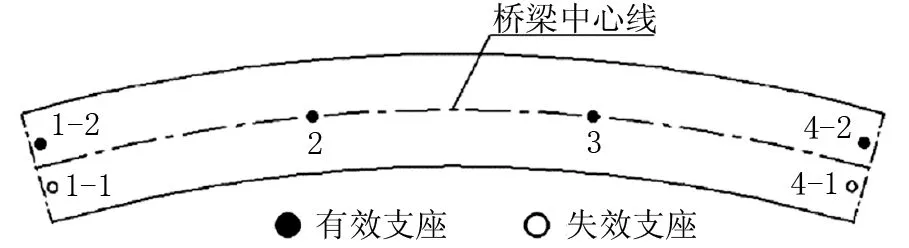
图2 曲线桥支座布置

研究对象为(35+35+30)m的预应力混凝土连续梁，利用有限元软件midas Civil分别建立直桥和曲率半径为100 m的弯桥模型进行计算分析，支座间距为3.5 m，取两车道左偏、中心对称布置、右偏的支座反力包络，直桥模型的支座约束形式如图3所示，弯桥模型的支座约束形式如图4所示。midas Civil提取支座并发反力，用CDN对两桥进行抗倾覆验算。

图3 直桥模型

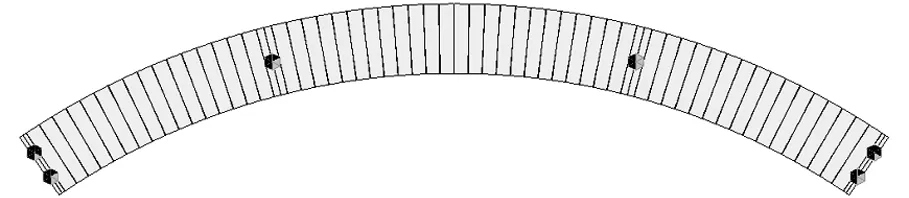
图4 R=100 m弯桥模型

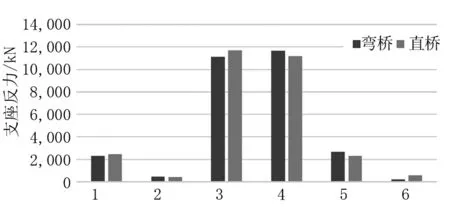
注：横坐标1～6分别代表1-1、1-2、2、3、4-1、4-2支座图5 直弯桥支座反力对比

在状态1，在1.0恒载+1.4车道荷载作用下，直桥最小支座反力位于1-1处，为393.7 kN；弯桥最小支座反力位于4-1处，为217.6 kN；在状态2，直桥抗倾覆系数为2.17<2.5，弯桥的抗倾覆系数为2.01<2.5，直弯桥的支座反力如图5所示，由以上数据可得出以下结论。

中支座反力最大，不论中支座是否固结，两边的抗扭支座反力较小；

直桥倾覆时梁体绕着1-1和4-1的连线，弯桥倾覆时梁体绕着1-1和2-3和4-1的连线，直桥抗力矩大于弯桥的，因此直桥的稳定系数大于弯桥，这和计算数据是相吻合的。

由于上述两桥状态2的抗倾覆系数均小于2.5，将中间2#支座均换成抗扭支座，支座间距4 m，直桥的最小抗倾覆系数为8.82，弯桥为8.05，满足规范要求。由此可知，中间设置抗扭支座(2+2+1+2模式)比中间点铰支座(2+1+1+2模式)稳定性更强，对梁体的横向抗倾覆性能有很大提升，但是直桥稳定性仍较弯桥好[5]。

取曲率半径分别为60 m，70 m，80 m，100 m，300 m，500 m，700 m的弯桥进行抗倾覆验算，其余条件同前，支座采用2+2+1+2模式，支座反力结果如图6所示。

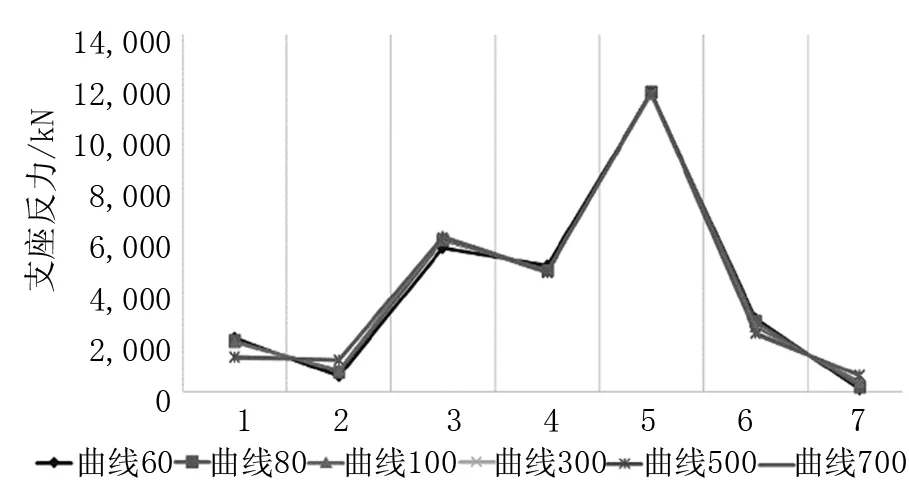
图6 不同曲率半径下支座反力

如图7所示，可得到以下结论。

在1.0恒载+1.4车道荷载作用下，2+2+1+2支座模式下，支座反力基本不随曲率半径的变化而变化，支座反力的大小分布保持稳定。

中间单支座反力和相邻中墩双支座合力基本一致，高于边支座反力，中间使用双支座可以降低支座反力峰值；

整体上看，曲率半径越大，抗倾覆稳定系数越大，在半径为60～80 m之间，抗倾覆系数基本保持不变，在300～700 m之间，抗倾覆系数基本不变，R=70 m时的抗倾覆稳定系数小于R=60 m的[6]。

3 温度对弯桥的影响

杭州萧山区工人路高架桥非机动车匝道由于温度作用导致梁体横向爬移，引起梁的刚体转动，最终倾覆[7]。本节研究在整体升降温作用和梁截面温度正负梯度分别作用下，弯桥梁体横向位移情况，模型仍取曲率半径为100 m，支座约束采用2+1+1+2模式，整体升温20 ℃，降温20 ℃，梁截面梯度温度按照《公路桥涵设计通用规范》(JTG D60—2015)4.3.12施加，考虑桥面100 mm的沥青混凝土铺装，T1=14 ℃，T2=5.5 ℃。

灰色线代表变形前梁体位置，由图8～图11可得到如下结论。

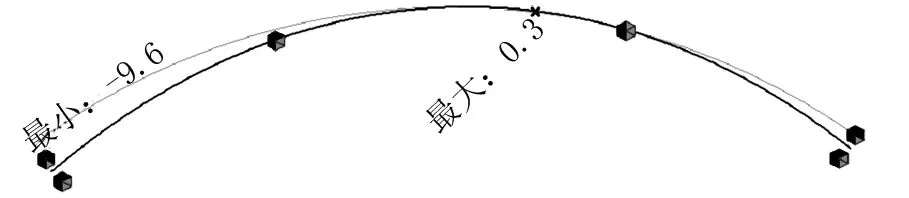
图8 升温下梁体横向位移(单位：mm)

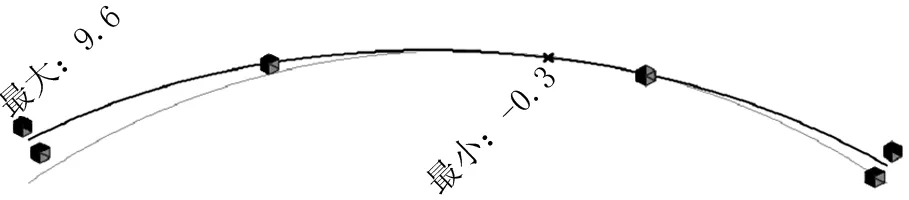
图9 降温下梁体横向位移(单位：mm)

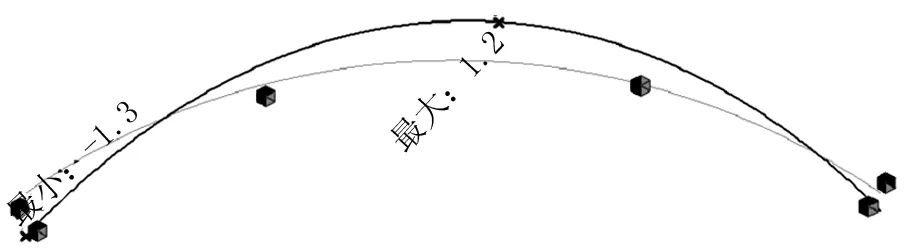
图10 正温梯梁体横向位移(单位：mm)

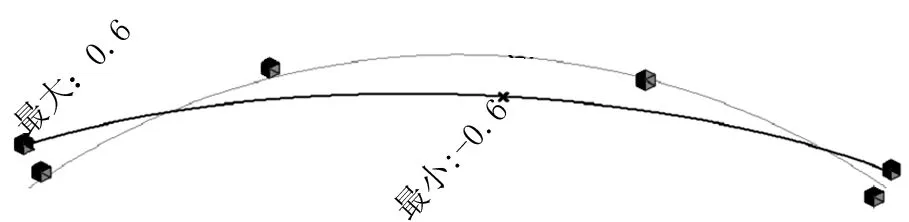
图11 负温梯梁体横向位移(单位：mm)

在系统升降温作用下，固结的中墩位置未发生变化，梁的两端分别发生同向的横向位移，升温作用下，梁体有增大曲率的趋势，降温则正好相反。

在梁截面温度梯度作用下，中墩支座和边支座处均发生横向位移，正温度梯度作用下，梁体有增大曲率的趋势，在负温度梯度下则相反。

横向位移随着曲率半径的增大逐渐减小，直梁未发生横向位移。

温度作用下的梁体横向位移一直是被大家所忽视的倾覆影响因素之一，因为侧向约束的存在，梁体横向位移较小，但是支座的侧向约束失效，梁体将发生很大的横向位移，中部的单支座对梁的偏心距亦增大，梁体发生刚性的转体失稳。

4 结 论

桥梁抗倾覆始于支座脱空，标志之一是梁体发生巨大转角，影响倾覆的因素主要有以下几点。

中支座脱空导致的反力重分配，边支座反力激增；墩和梁之间存在的水平力，梁体发生转角的时候会对墩顶产生水平力，水平力同时会增大偏心距，可能导致梁体下滑，继而又增加墩顶的水平力，形成恶性循环；温度作用下的梁体横向爬移。[8]

对比分析直桥和弯桥的抗倾覆性能，得出以下结论。

中支座反力最大，不论中支座是否固结，两边的抗扭支座反力较小；

直桥倾覆时梁体绕着1-1和4-1的连线，弯桥倾覆时梁体绕着1-1和2-3和4-1的连线，直桥抗力矩大于弯桥的，因此直桥的稳定系数大于弯桥，这和计算数据是相吻合的。

由于上述两桥状态2的抗倾覆系数均小于2.5，将中间2#支座均换成抗扭支座，支座间距4 m，直桥的最小抗倾覆系数为8.82，弯桥为8.05，满足规范要求。由此可知，中间设置抗扭支座(2+2+1+2模式)比中间点铰支座(2+1+1+2模式)稳定性更强，对梁体的横向抗倾覆性能有很大提升，但是直桥稳定性仍较弯桥好。

对比不同曲率半径弯桥抗倾覆性能得出以下结论。

在1.0恒载+1.4车道荷载作用下，2+2+1+2支座模式下，支座反力基本不随曲率半径的变化而变化，支座反力的大小分布保持稳定；中间单支座反力和相邻中墩双支座合力基本一致，高于边支座反力，中间使用双支座可以降低支座反力峰值；整体上看，曲率半径越大，抗倾覆稳定系数越大，在R=60～80 m之间，抗倾覆系数基本保持不变，在300～700 m之间，抗倾覆系数基本不变，R=70 m时的抗倾覆稳定系数小于R=60 m的。

系统温度和截面梯度温度对梁体横向位移影响得出以下结论。

在系统升降温作用下，固结的中墩位置未发生变化，梁的两端分别发生同向的横向位移，升温作用下，梁体有增大曲率的趋势，降温则正好相反；在梁截面温度梯度作用下，中墩支座和边支座处均发生横向位移，正温度梯度作用下，梁体有增大曲率的趋势，在负温度梯度下则相反；横向位移随着曲率半径的增大逐渐减小，直梁未发生横向位移。

5 建 议

单支座横向稳定性不及双支座，但不是说一定不能使用单支座，在条件允许下，可优先选用双支座，严禁超载现象。

桥梁倾覆过程中存在明显的几何非线性，还需进一步研究。[9]

车辆荷载分布有很大的区域性，车辆荷载形式也有较大差异，倾覆稳定系数2.5的取值是否能涵盖所有地区，值得深入研究。

常规的抗倾覆验算同时需要进行上下部结构的验算。