基于M-N曲线包络的钢筋混凝土拱桥加固效果量化评价方法

杨 旭

(重庆国际投资咨询集团有限公司，重庆 400020)

钢筋混凝土拱桥以其兼具拱桥优美的造型以及因拱桥特有的结构受力特点而使得钢筋混凝土性能得到充分的利用与发挥，而得到广泛应用。现已有诸多研究关于其运营中的检测、评价和加固[1～5]，程进等[1]分析了拱桥极限承载力的研究现状；肖魏兵等[4]建立了一种评定结构耐久性的模糊综合评定法以推断桥梁加固前后的使用寿命；任立冬[5]基于实桥检测结果，建立修正的混凝土拱桥初始模型进行承载力分析。从偏心受压截面承载能力极限状态出发，对各拱圈截面加固前后内力的设计值进行分析，引入承载力相对冗余值的概率，提出了一种基于M-N曲线包络的钢筋混凝土拱桥加固效果评价方法，并利用工程实例进行分析。

1 基于M-N曲线的偏心受压截面极限承载力计算

1.1 基本假定

为便于分析，常作如下假定[6]：

(1)截面变形服从平截面假定。

(2)钢筋和混凝土的应力-应变关系如式(1)、(2)所示

σs=Esεs，σs∈[-σy，σy]

(1)

(2)

式中：Es为钢筋的弹性模量，fc为混凝土的抗压强度，ε′和εu分别为混凝土的峰值压应变和极限压应变。

(3)构件的变形很小，不影响构件的受力体系计算图形和内力值。

(4)一般不考虑时间(龄期)和环境温度、湿度等影响，即忽略混凝土的收缩、徐变和温湿度变化引起的内应力和变形状态。

(5)忽略拉区的混凝土作用。

1.2 计算原理

大、小偏心破坏形式的界限状态[7～9]为：当受拉钢筋达到屈服应变εy时，受压边缘混凝土也刚好达到极限压应变εu，如图1所示。

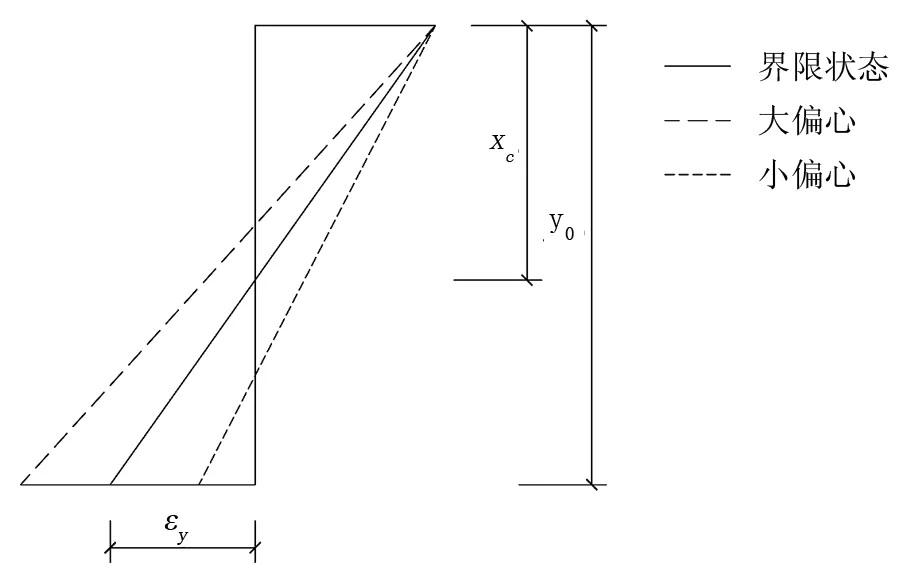
εy-钢筋屈服应变；εu-混凝土极限压应变；h0-截面受压较大边边缘至受拉边或受压较小边纵向钢筋合力点的距离图1 大小偏心受压界限破坏应变

其中xc为按平截面假定得到的界限破坏时受压区混凝土高度，等效矩形应力分布图的受压区高度为x=0.8xc；受拉侧钢筋应变εs可以由式(3)表达。

(3)

根据偏心受压截面的极限状态和大、小偏心受压界限状态的分析，可以得出主拱圈正截面强度计算图示[10]。

以受压区高度为自变量，可以建立一种包括大、小偏心受压情况的极限承载力计算公式[10]，如式(4)～(5)所示。

(4)

(5)

式中：σs=Esεs，且应满足σs∈[-σy，σy]，即当σs计算值超过钢筋的屈服强度时，取其屈服强度为计算值。

2 基于M-N曲线包络的钢筋混凝土拱桥加固效果评价方法

对于钢筋混凝土拱桥结构来说，在已知其截面参数和材料信息后，以相对受压区高度x为自变量，根据公式(4)、公式(5)可以迅速得到各截面的M-N曲线包络图。对任意拱圈截面，其设计内力值可以用M-N曲线图中的坐标点R(M，N)表示，如图2所示。

M-弯矩设计值；N-轴力设计值；M0、N0-M-N包络图上最近点对应的弯矩值和设计值图2 内力值在M-N曲线包络图中的表示

图中点R(M，N)到包络线上最近点R(M0，N0)距离r称为承载力冗余值，当点R(M，N)在包络图内时，r为正值，其承载力满足要求；当R(M，N)点在包络图外时，r为负值，承载力不满足要求。

套箍加固法是钢筋混凝土拱桥加固中最常用的方法之一[11，12]，由于加固层和原拱圈结构二次受力情况的存在，难以准确地计算组合截面的承载力，且其计算值无法反应原拱圈的受力变化[13]。考虑到加固前后其原拱圈的参数并未发生改变，即其自身的M-N曲线并未改变，改变的只是由于加固层参与受力而发生变化的内力值，将加固后原拱圈的内力值分别代入M-N曲线包络图，则可以直观地看出加固后各截面是否符合受力要求。

3 工程实例及其分析

3.1 桥梁概况及加固方案

重庆市关二嘴大桥为跨径80 m、矢跨比1/8的上承式钢筋混凝土拱桥，拱圈材料为C40混凝土，拱肋为矩形实心截面，高0.7 m，宽0.4 m，横向共4片拱肋，桥面全宽8 m。根据检测报告，该桥拱肋拱轴线下挠严重且局部有开裂现象，技术状况等级为4类，处于较差状态。建立有限元模型验算主拱圈承载力(公路-Ⅱ级)，结果表明主拱圈部分截面承载力不足。

加固方案为对主拱圈进行C40混凝土套箍封闭加固，拱背及拱腹加固层为15 cm，拱肋侧面加固层为10 cm。考虑到原桥承载力严重不足，对原结构表观病害进行处理后，由拱脚至拱顶按照立柱间距分段对称进行加固，待浇筑段强度达到设计值的75%时进行下一阶段的浇筑。达到设计要求强度的混凝土可以有效分担后续施工过程中新增的荷载，有利于保证施工过程中结构的安全。采用套箍加固主拱圈前，通常先拆除拱上建筑以减轻结构自重，使得加固层能分担更多的恒载。

3.2 加固效果评价

荷载组合方式为1.2×恒+1.4×活载(最小)。以2#拱肋为例，分别提取不加固、直接加固和拆除拱上建筑后加固三种情况下的内力组合值，并代入M-N曲线包络图进行分析，如图3～图5所示。

图3 加固前各截面内力分布

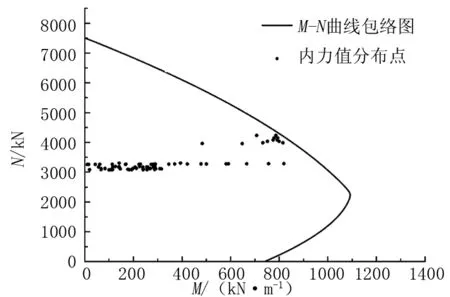
图4 直接加固后各截面内力分布

图5 拆除拱上建筑加固后各截面内力分布

从图3～图5可以看出，加固前各截面内力点大部分分布在包络线外，表明其承载力严重不足，在两种加固方法加固后各截面内力值均能有效包络，但是拆除拱上建筑后，各点分布相对远离包络线，表明其加固效果更好，结构安全储备更高。

为进一步量化分析两种加固方案的加固效果，结合M-N曲线，利用数值软件编程，可以迅速得到各截面的相对冗余值。以各截面顺桥向位置为横坐标，相对冗余值为纵坐标，得到主拱圈不同工况下的相对冗余值曲线，如图6所示。

图6 不同工况下承载力相对冗余值曲线

其中，工况1曲线大部分位于0以下，表明加固前主拱圈大部分截面承载力严重不足；工况3曲线绝大部分位于工况2曲线之上，表明拆除桥面系后再进行套箍加固能有效减轻原拱圈的负担。将曲线中的数据进一步量化，得到各曲线的期望和方差如表1所示。

表1 不同工况下相对冗余值曲线的数值特征值

从表1中可以看出，工况3的期望为0.42，方差为0.05，表明在拆除桥面系后再进行套箍加固时，能极大地优化结构受力情况，使得原拱圈各截面承载力平均留有42%的富余量；相对工况2直接套箍加固时，其方差更小，表明原拱圈在加固后各截面受力更为均匀、合理，有利于结构的长期安全。

4 结 论

(1)建立了一种包括大、小偏心受压情况的极限承载力计算公式，可以便捷地得到已知参数截面的M-N曲线包络图，利用该包络图可以直观判断拱圈加固前后内力分布状况。

(2)结合数值理论，提出了承载力相对冗余值的概念，该方法根据加固前后拱圈冗余值曲线的期望和方差等数值特征信息，可以准确地量化加固效果。值得一提的是，结合的实际工程为一采用套箍加固的矩形等截面钢筋混凝土肋拱桥，但采用其他加固方式和截面类型的钢筋混凝土拱桥也可按此原理进行评估。