基于改进人工势场法的船舶自动避障系统研究
郑云峰,于俊迪
(大连海事大学 航海学院,辽宁 大连 116026)
0 引言
船舶自动避障系统是近年来全世界航海学者们研究的热门课题,在此期间,诞生了诸多避障算法,不再赘述。在诸多方法当中,人工势场法深受学者们的喜爱。它具备数学原理简略、安全性高、实时性等优点[1]。人工势场法的固有问题是众多学者的钻研重点,对于极小值问题,文献[2]运用动态法向力,文献[3]利用公式推导的方式去调整势场函数参数,文献[4]设置子目标,文献[5]提出了虚拟流水法,文献[6]设置了中间目标法。对于目标不可达问题,文献[2]在斥力函数中引入距离影响因子。
本研究针对人工势场法的固有问题提出相应的解决办法且对人工势场进行改进,构建了船舶自动避障系统,利用matlab仿真平台进行验证。
1 连锁网络法
在运用连锁网络法进行船舶避障中,障碍物默认为静态障碍物,它被分为2类,一类是“可视”障碍物,另一类是“不可视”障碍物。
如图1所示,以本船为原点,分别做过障碍物1、2的虚射线,以实线段连接障碍物1、2。那么,障碍物1、2称为相对于本船的“可视”障碍物,障碍物3因被实线段遮挡而被称为相对于本船的“不可视”障碍物。“可视”障碍物是船舶避障的主要研究对象,即对“可视”障碍物进行连锁,而后船舶采取有效的避障方式进行避障,连锁网络算法的实现步骤为:
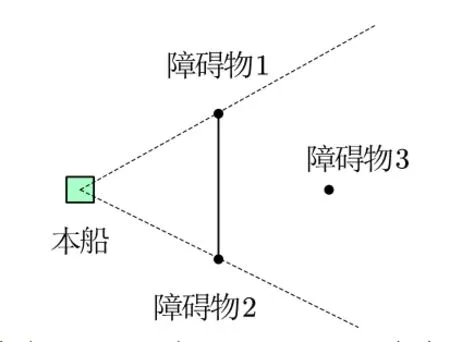
图1 可视与不可视示意图
1)设置2个障碍物之间的“连锁”距离(记为S1),以选定的静态障碍物a为圆心,S1为半径的区域内搜寻其他的障碍物,在搜索到的障碍物中选择相距本船最近的障碍物,记为障碍物b,将障碍物a与b进行连锁。如果在搜寻范围内无其他障碍物,则障碍物a被看成单个障碍物来进行船舶避障,被连锁的障碍物看作一个完整的障碍物。对于“连锁”距离的设定,相关研究没有具体标准,只是说明“根据本船与障碍物的距离进行实时调整”。2)将“不可视”障碍物剔除连锁运算。3)选择次近的“可视”障碍物且没被连锁、遮挡的,重复上述过程,遍历全部的障碍物。4)对于已经连锁终了、数目为2个以上的障碍物且之前没连锁的,进行连锁。
2 改进的人工势场法
2.1 引力势函数的改进
在原有引力势函数的基础上,引入速度引力函数,这样可更精准、快速地追踪目标点。加入速度势函数后,

2.2 斥力势函数的改进



当a=1时,为该分力原本的方向,当a=-1时,则为该分力原本方向的相反方向,后续以此来控制船舶的转向。
在改进的人工势场法后,本船与障碍物的速度矢量关系以及受力关系示意图,如图4所示。

图2 速度引力向量示意图
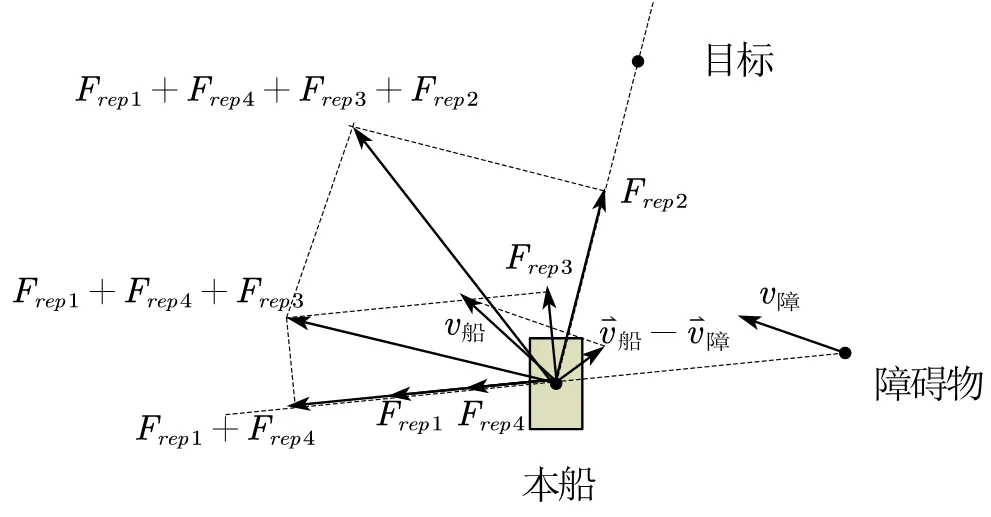
图3 改进斥力势场中本船受力示意图
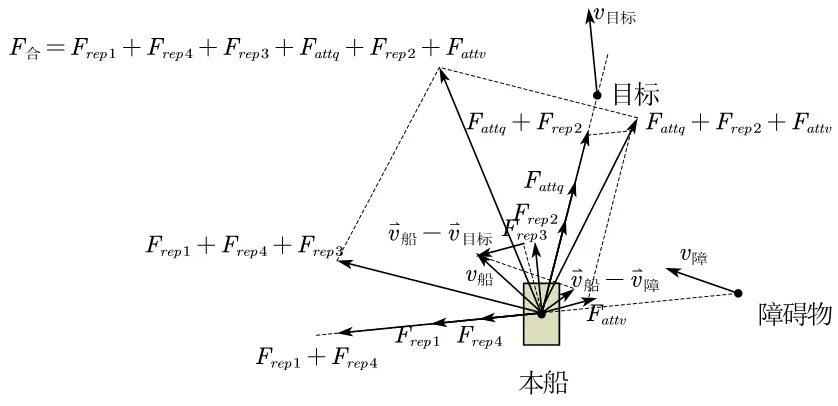
图4 综合受力示意图


2.3 改进的动态分阶人工势场法

3 船舶自动避障系统
在改善的动态分阶人工势场法的基础上,创建船舶自动避障系统。通过AIS或ARPA等助航仪器获得本船的航行环境信息,再联合改良的动态分阶人工势场法,计算出虚拟动态目标点,对本船产生的引力Fatt(x)以及障碍物对本船产生的斥力Frep(x),叠加得到合力F合(合力的方向为指令航向)。本船的指令航向由合力的方向决定,将本船的航向误差作为输入,使用PID自动舵产生适宜的舵角,从而控制本船的航行,完成航迹维持、避障、恢复航迹。自动避障算法流程图,如图5所示。

图5 改进人工势场法的船舶自动避障算法流程图
4 仿真实验与分析
4.1 仿真实验及分析
1)实验说明
设定实验中的船舶皆不属于《国际海上避碰规则》中第18条款规定的需他船让路的船舶;船舶的运动数学模型均采用Abkowitz型,在实验中运用“Mariner”轮的流体动力导数及其他船舶参数;在所有实验仿真中,均加入了定常、均匀流的干扰因素。仿真实验中,PID型自动舵部分实验参数:k1、k2、k3皆取值为1;Kw与n皆取值为2;dre为0.01 n mile;rgoal为6 n mile;Sda为1.8 n mile(动态船舶)、1.2 n mile(静态障碍物)。本研究利用改进的动态分阶势场算法的自动避障系统,在仿真中实验了船舶避障中遇到的局部极小值、多船+局部极小(复杂情况)的场景。仿真实验中,红色代表本船航迹,蓝色为障碍船航迹。
2)仿真实验
仿真实验1:局部极小值情形。利用Matlab仿真实验平台验证了连锁网络法对于船舶避免局部极小值时的有效性,仿真实验截图如图6所示。以Ta和Tb等时刻的仿真图表示未使用连锁网络法时本船的航迹情况,Ta<Tb。以Td<Te时刻的仿真图表示在使用了连锁网络法后,本船的航迹,Td<Tc。可以看出,当没使用网络连锁法且遭遇局部极小值时,本船将徘徊于一定的区域内,无法继续航行。当使用了连锁网络法后,本船可以平滑地绕过局部极小值区域,且能恢复航迹[7]。

图6 仿真实验1
仿真实验2:多船+静态障碍物避障,即混合避障的复杂情况。实验参数如下,位置坐标的单位为n mile。设置本船航速为15 kn,初始位置为(0,0.5),初始航向为45°。障碍船的速度分别为15 kn、13 kn、9 kn、9 kn,对应的初始位置为(26,30)、(30,26.5)、(31.3,3)、(32.3,3),对应的初始航向为225°、210°、310°、310°。静态障碍物的位置分别为(4,5)、(11,7.7)、(11.5,9)、(10.5,9.5)、(9.5,9.3)。避让静态障碍物时的引力系数K=1,K2=1.5,斥力系数K1=0.2×107、K4=0.7×104、K3=0.7×104。避让动态障碍船时,引力系数不变,斥力 系 数K1=0.2×107、K4=0.3×104、K3=0.7×104×0.8、K5=0.7×104×0.8。水流流向为东北向45°,流速为1 kn。避让等级P0为4 n mile,CRI0为0.45,tcpa=10 min,本船与动态障碍物的SDA设置为1.8 n mile、静态障碍物为1.2 n mile。dre为0.01 n mile,Rgoal为6 n mile。图1~图3显示了本船在这4个时刻的航迹,T图1<T图2<T图3,D=0.3 n mile即在恢复航迹阶段时,本船与原航迹的距离小于0.3 n mile时就认为已恢复到原航迹。可以看出,本船在船舶自动避障系统的引领下,可以无碰撞地、安全地避开障碍物,且能恢复航迹。

图7 仿真实验2
4.2 仿真实验分析
1)避障安全性分析
为了验证船舶在避障过程中能以安全距离通过障碍物且没有碰撞危险,取仿真实验2,计算了在本船避障中与动态、静态障碍物的距离、与动态的船舶CRI的变化,见图8~图10。可以看出,本船可以在设置的安全距离以上通过障碍物且没有碰撞危险,这足以说明船舶避障系统使用的安全性[8]。
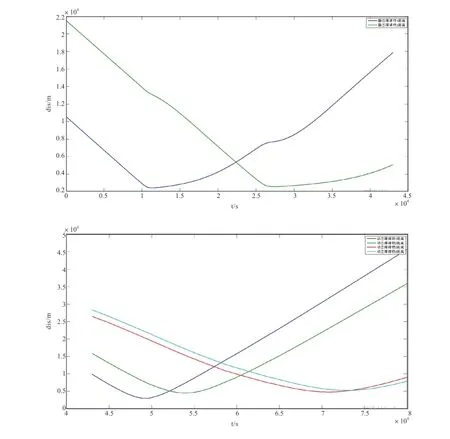
图8 本船到静、动态障碍物的距离变化图
2)航迹恢复能力分析
取仿真实验2,计算本船与原航迹的距离。根据图10可以看出,本船在避障结束后可以较快地恢复航迹,即恢复到本船与原航迹的距离是在预先设定距离D的范围内,证明了船舶自动避障系统具有较好的航迹恢复能力。
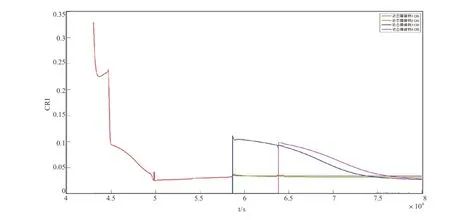
图9 本船与他船的碰撞危险(CRI)变化图

图10 本船到原航迹的距离示意图
3)航向稳定性分析
取仿真实验2,计算本船的航向变化趋势。从图11可以看出,本船在避障开始前及航迹恢复后,航向都能稳定在原航向的附近,证明了船舶避障系统可以保持航向。

图11 本船的航向变化图
5 结语
本研究在相关学者研究成果(动态分阶人工势场法)的基础之上,对动态分阶势场进行改进,对公式进行改进,考虑了船舶避让静态障碍物的情况,解决了遭遇局部极小值的问题,完善了船舶自动避障系统。在Matlab仿真实验中,添加了定常、均匀流的影响因素,根据实验结果可知,经完善、改进后的船舶自动避障系统具有航迹维持能力、引领船舶安全有效的避开障碍物以及避障后的恢复航迹能力,且船舶的避让行动完全契合了《国际海上避碰规则》中的要求。在日后的研究中,应把风、浪以及岸壁效应等综合因素考虑进来,进一步完善、验证船舶自动避障系统。

