基于矩阵分解的协同过滤地球站优选推荐方法
孙雪苗,赵洪华,胡谷雨
(陆军工程大学指挥控制工程学院,江苏 南京 210007)
0 引言
随着卫星通信技术的发展,人类需要对卫星通信的适用场景进一步探索。以海洋通信为例,目前海上远程通信与高速实时数据传输手段已成为海洋信息化建设的主要技术瓶颈,而卫星通信因其运行稳定、干扰少、组网灵活、通信成本与距离无关、可提供不受地理环境限制的广域覆盖等优点,被认为是最有效的海上通信手段之一。
通常情况下,如在海上的舰船,相当于移动站,它只能依靠卫星通信与内陆(固定站)保持宽带通信联系。如图1所示,用户A 是处于固定站所覆盖区域,用户B 则位于移动站上,用户A 与用户B 之间的通信路由为:用户A—地球站A—通信卫星X—地球站B—用户B。在用户A 和用户B 的通信中,关键是固定站A 和移动站B 之间的卫星通信,因为用户B 处于移动中且远离陆地,所以两者之间的通信只能使用卫星通信网络。在此情形中,能够与移动站B 满足可互通条件的固定站数量可能有很多,而卫星的信道资源是有限的,在紧急求援,或是极端情况下,不需要将所有的固定站与移动站B 都组建在同一个子网中,需要选择部分固定站,而选择哪些固定站,这就是本文所研究的地球站优选推荐组网问题。

图1 固定用户与移动用户通信示意图
基于上述有关地球站优选推荐组网的介绍,本文首先对此问题建模,并基于矩阵分解的协同过滤推荐算法提出一种地球站优选组网方法,预测固定站与移动站间的卫星通信质量,从而尽量选择最优的固定站与移动站组建在同一子网中。
1 模型
在系统模型中,各型号地球站可形式化为:

其中为一个二元组(X,Y),表示地球站ES所在的地理位置。假设每个地球站只有一幅单频段天线,同一个地球站的信道单元共用该地球站的天线和射频线路,天线所支持的射频工作频段为ES,在实际系统中具体可以划分为C,Ku,Ka 等频段,其中ES表示天线所支持的射频频段的上限,ES代表天线所支持的射频频段的下限;ES代表地球站的天线极化方式,可划分为线极化和圆极化两种模式,具体地,线极化模式可根据实际通信需求调整为水平和垂直极化,圆极化模式可调为左旋圆极化和右旋圆极化。G表示地球站的信号发送幅度增益(dB),其数值等于发射机功放增益和天线发射增益之和。G为地球站天线的信号接收增益(dB)。P为地球站功率放大器的最大输出功率(W),{}为地球站ES支持的CU集合。
本文中移动站与固定站均为地球站,其中用ES表示固定站,ES表示移动站。
在模型中,所讨论的通信卫星均为地球同步通信卫星,各卫星可以形式化为:

在式⑵模型中假设卫星均为多波束卫星,且只有一副天线,其中S表示其支持的射频频段,S代表其射频频率的上限,S代表其射频频率的下限;S为该天线的极化方式,支持的点波束数量为个。表示卫星波束的覆盖地理范围,因此卫星覆盖范围是各个波束覆盖范围的并集=∪∪…Area,{Tp}为卫星透明转发器。
在与用户的实际通信处理过程中,发送信息前必须经过源地球站上的信道单元,再通过卫星转发后送达目的地球站上。一旦接收地球站达到了规定要求,则能够在同一颗卫星下完成“一跳通信”;否则,信号就需要通过地面关口站转发,经历“两跳”到目的地球站上。
在固定站和移动站的组网任务中,子网构建参数可形式为:

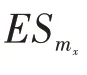

2 基于矩阵分解的协同过滤地球站优选推荐方法
本文综合考虑固定站与移动站之间的历史通信矩阵特性,并提出基于矩阵分解的协同过滤算法对各移动地球站进行了优选推荐。首先,由于矩阵法分解的协同过滤算法的输入是稀疏的物品用户评价矩阵,在此情形下,可以将移动站视为用户,固定站看作物品,则该输入就可以演变为固定站移动站的评分矩阵。其次因为历史通信指标不止一个,而移动站对固定站的评分是一维的,所以需要用到主成分分析方法,将多维特征映射到一维上,此时该一纬特征仍然包含了之前多维特征的信息,可以将该一维特征看作移动站对固定站的评分。得到了矩阵分解算法的输入后,根据Funk-SVD矩阵分解原理求解地球站优选推荐组网模型。
2.1 数据预处理
在本节中,主要解决矩阵分解算法的输入矩阵。假设共用个移动站,个固定站,首先从历史通信指标出发,本文采用了两个历史通信指标,分别是呼通率和丢包率可以得到二个×矩阵分别为:S,S。则基于主成分分析方法求解评分矩阵的算法流程如下:

2.2 基于矩阵分解的协同过滤地球站优选推荐算法流程
根据Funk-SVD 矩阵分解原理,且在上一小节中已经得到了将该算法需要的输入矩阵,因此本节中可以按照矩阵分解的流程进行。其中设置初始化迭代运算轮数为。

则为拟合后的移动站固定站评分矩阵,则在此矩阵中根据评分的大小就可以为移动站推荐通信质量优质的固定站进行通信。
3 仿真与分析
3.1 仿真环境参数设置
在整个仿真模拟过程中,为了简化问题,我们假设:①每个地球站的功放增益和接收天线增益都足够大,即满足信号可接受条件;②每个通信波束对应一个转发器,且转发器带宽容量相同。最终的仿真参数如表1所示。
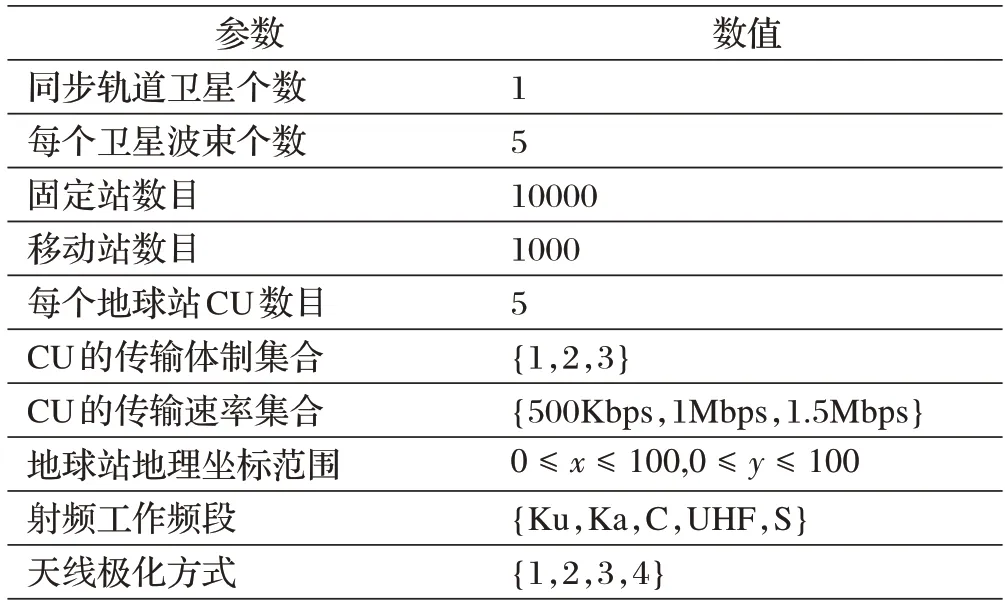
表1 地球站优选推荐仿真参数表
3.2 实验结果分析
针对本文讨论的地球站优选组网问题,目前还没有专门解决该类问题的算法。现阶段,为移动站选择组网的固定站主要是为人工决策,即通过人工选定固定站与移动站组网。因此,为验证本文提出的基于矩阵分解的协同过滤地球站优选推荐算法,采用随机组网算法和贪婪组网算法作为对比算法。
为了对比三种算法在地球站优选推荐中的效果,进行了五次组网任务。在五个组网任务中,如图2所示,利用本文算法得到的组网规划方案都具有更高的呼通率,贪婪算法比本文算法较差,随机组算法效果最差。在每次的组网任务中,本文算法都比其他两个算法具有更高的呼通率,贪婪算法由于其根据已知的呼通率选择固定站组网,可能忽略某些可互通但未发生通信关系,且性能较好的固定站,因此贪婪算法虽然在其中一两个组网任务中获得和本文算法几近相同的呼通率,但是在所有任务中,都没有超过本文算法的呼通率,因为本文所提出的基于矩阵分解的协同过滤算法可以在全局挑选通信质量最优的地球站进行组网,而随机算法是一种非常随机的组网方式,其结果具有很大的随机性,是一种较差的组网方式。

图2 不同优选组网算法在不同组网任务上得到的呼通率
接下来,考察丢包率,从图3 可以看出,在五个组网任务中,本文算法相较贪婪算法和随机算法具有更低的丢包率,同样是因为本文提出的基于矩阵分解的协同过滤算法,可以尽量在全局上选择丢包率更低的固定站组网,能够挖掘卫星通信质量评价矩阵更潜在的信息。而贪婪组网算法只能根据已知的丢包率数值选择固定站,无法兼顾更多的通信质量指标。随机组网算法仍然是其中最差的一种组网方式。

图3 不同优选组网算法在不同组网任务上得到的丢包率
4 结束语
针对卫星通信资源受限、地球站选择影响通信质量的问题,本文首先对卫星通信地球站优选组网问题作形式化描述,选取两种指标作为评估通信质量的指标,针对移动站与固定站通信质量指标多维的问题,使用主成分分析方法将多维数组降为一维数组,得到移动站对固定站的评分矩阵,随后使用矩阵分解的协同过滤算法求解地球站优选推荐组网问题。实验结果说明,本文提出的基于矩阵分解的协同过滤地球站优选推荐组网算法比贪婪组网算法和随机组网规划算法具有更高的呼通率,更低的丢包率。接下来,可进一步研究对更多通信指标下的地球站进行优选。

