复杂受光条件下光伏阵列输出特性建模分析
李光金,韩会宾,傅 饶,石嘉川
(1.山东建筑大学信息与电气工程学院,山东 济南 250101;2.中铁工程设计咨询集团有限公司济南设计院)
0 引言
随着双碳目标(碳达峰,碳中和)的提出,太阳能被认为是未来最有发展前途的新能源,光伏发电作为太阳能开发利用的主要技术,得到了广泛应用。目前已有多种光伏电池模型,通过对各种光伏电池数学模型的输出特性曲线研究发现,每个光伏电池模型之间没有实质性差异,仅复杂性和实用性不同,输出特性曲线均为非线性曲线,正常光伏阵列在均匀受光条件下功率输出曲线只有一个峰值,即最大功率点。如今许多BIPV(光伏建筑一体化)建筑为了满足建筑美学要求,已不再将所有光伏组件设计成单一朝向,致使光伏阵列受光不均匀,光伏组件不规则排列可能会在一定程度上影响发电效率。另外,光伏组件的局部阴影问题会导致光伏组件发电不均衡,严重降低功率,甚至还会造成热斑效应。若存在复杂受光下光伏模块串联,光伏阵列输出曲线会发生变化,输出功率也会降低,传统的光伏阵列数学模型也不再适用。
本文对均匀光照下光伏电池的输出特性数学模型进行仿真研究,并在此基础上推导建立了串联光伏阵列在复杂受光条件下的输出特性数学模型,利用Matlab/Simulink 软件仿真,实现复杂受光条件下光伏阵列的输出特性分析,为后续MPPT 算法及光伏阵列布置奠定基础。
1 光伏电池建模及分析
1.1 光伏电池数学模型
综合考虑光伏电池模型的复杂性和实用性,对常见的单二极管光伏电池模型(如图1所示)进行数学建模,利用Matlab/Simulink 软件仿真分析其输出特性曲线。

图1 光伏电池简化的等效电路
图1 中,I表示直流电流源的电流,用于模拟光生电流,A;二极管为电池内部等效P-N结,I为二极管旁路电流,A;R和R表示光伏电池内部的等效串联电阻和并联电阻,Ω;I为并联电阻旁路电流,A;为光伏电池输出电流,A。
根据基尔霍夫电流定律,光伏电池输出电流表达式为:

光生电流I表达式为

二极管旁路电流I的数学表达式为
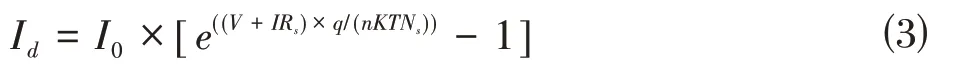
其中为二极管的饱和电流,表达式为

I为二极管的反向饱和电流,表达式为

并联电阻旁路电流I表达式为

式⑴~式⑹中,k表示电流温度系数(25℃);表示太阳辐射能,W/m;表示工作温度,K;T表示标称温度,K;q 表示电子电荷,C;V表示开路电压,V;I表示短路电流,A;n 表示二极管的理想因子;K 表示玻尔兹曼系数,J/K;Eg0 表示半导体的带隙能量,J;N表示串联单元数。
1.2 光伏电池输出特性
本文采用Matlab/Simulink 软件对公式⑴-⑹进行仿真建模,对光伏电池在不同光照强度下的输出特性进行仿真和分析,绘制曲线所用到的一些常数列表如表1 所示,该参数取自Simulink 光伏电池模块的1Soltech 1STH-215-P型号。

表1 单二极管光伏电池数学模型参数
光伏电池的Matlab/Simulink 仿真结果和曲线如图2所示,三条曲线为在25℃恒温下,光照强度分别为1000W/m、800W/m、500W/m下的和曲线。由曲线可知,随着光照强度的增加,光伏电池的短路电流将显著增加,光伏电池的开路电压将略微增加。由曲线可知,随着光照强度的增加,光伏电池的输出功率会随之提高,相应的最大功率点也会提高。然而,在不同的光照强度下,对应于最大功率点的电压几乎没有差异。每种光照强度下,光伏阵列只有一个峰值点,即最大功率点,用传统的MPPT算法可以方便找到最大功率点。因此,光照强度是光伏阵列电气输出特性主要影响因素。

图2 不同光照强度下光伏电池输出曲线
2 复杂光照强度下的光伏阵列建模仿真
2.1 串联光伏阵列数学模型的建立
在实际的光伏应用中,光伏组件应进行串联,以提高系统输出电压,如图3 所示,组成一个光伏阵列。若每个光伏模块接收到的光照强度不同,则光伏阵列的电气输出特性曲线就会产生变化,原有的数学模型也不再适合,本文将接收到相同光照强度的光伏电池进行串联列为一组光伏模块,多个光伏模块再串联组成一个光伏阵列,使其接收多种光照强度,对光伏阵列进行数学建模,研究其电气输出特性规律,其中G、G、…、G表示光照强度。

图3 光伏组件串联结构图
每个光伏模块的光生电流分别为I、I、...、I,输出电流分别为I、I、...、I,输出电压分别为V、V、...、V,由于公式⑹中的并联电阻R往往很大,使I远小于输出电流,故此项可以忽略不计,则每个光伏模块的输出伏安特性公式为:

当光伏阵列接受到的光照强度均匀一致时,串联光伏阵列总输出电流即为各光伏模块输出电流,总输出电压、总输出功率分别为各光伏模块输出电压之和、输出功率之和。设有个光伏模块串联,即:
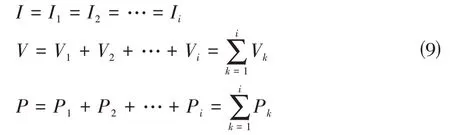
因此,当光伏阵列中各光伏模块接收到的光照强度均匀一致时,串联光伏阵列输出特性的数学模型仍为:
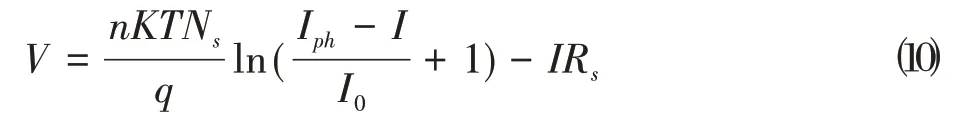
当光伏阵列接受到光照强度不一致时,公式⑽则不再适用,为了分析光伏阵列的复杂受光情况,假设共个不同光照强度的光伏模块串联,光照强度分别为G、G、…、G,并且G>G>…>G,由公式⑵可知,I>I>...>I。
当串联光伏阵列外接负载电阻很小,即光伏阵列输出电流很大,输出电流为I<I ≤I时,光伏模块2到光伏模块并联的二极管形成正向偏压,旁路二极管导通,使得光伏模块2 到光伏模块被短路,不再工作,此时只有光伏模块1正常工作,此时光伏阵列的输出特性方程即为光伏模块1的输出特性方程,即:

随着光伏阵列外接负载电阻逐渐变大,光伏阵列输出电流逐渐变小,输出电流为I<I ≤I时,此时与光伏模块2 并联的旁路二极管处于反向偏压,旁路二极管不再导通,光伏模块2 正常工作,但光伏模块3 到光伏模块的旁路二极管仍处于正向偏压导通状态,光伏模块3到光伏模块依旧不工作,此时光伏阵列由光伏模块1 和光伏模块2 共同工作,光伏阵列的输出特性方程为:

以此类推,当光伏阵列外接负载最大,即光伏阵列输出电流最小,输出电流此时为0≤I ≤I,此时所有光伏模块均处于正常工作状态,光伏阵列输出特性方程为:
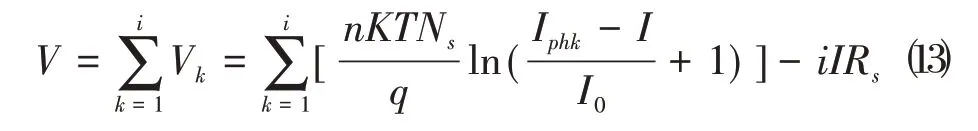
综上所述,当光伏阵列处于复杂受光条件下时,光伏阵列的输出特性因旁路二极管的存在而发生改变,串联光伏阵列的输出特性方程转化为分段函数的形式,当有种不同光照强度的光伏模块串联在一起时,并且I>I>...>I>I,串联光伏阵列的输出特性方程为:

2.2 串联光伏阵列输出曲线仿真分析
本节对复杂光照下串联光伏阵列数学模型进行仿真研究,以三组光伏模块为例,采用Matlab/Simulink软件对三组光伏模块串联做仿真设计,分别采用不同的受光形式研究其输出曲线,Simulink 建模如图4 所示,温度设定为恒温25℃,仅对不同光照强度下的光伏阵列电气输出特性曲线进行研究和分析。
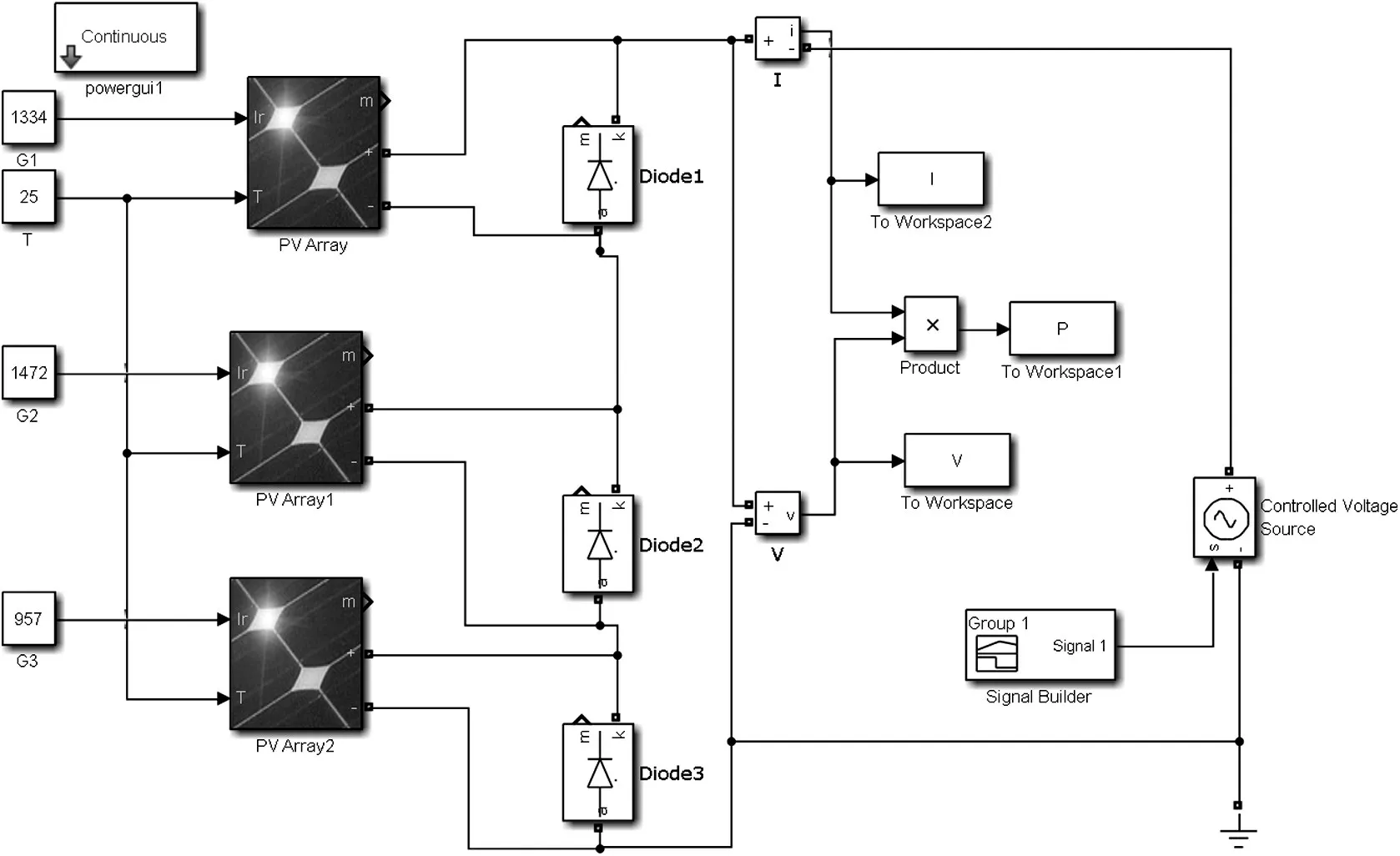
图4 复杂光照下的光伏阵列建模
本文以济南某光伏建筑为例,由济南地区全年太阳辐射量以及太阳辐射度模型可知太阳辐射度与光伏组件倾角的关系。济南地区光伏组件最佳倾角为30 度,对应光照强度为1472W/m,通过调节光伏组件倾角的方法改变光照强度,济南地区全年太阳辐射量如表2所示,该数据取自Meteonorm数据库。

表2 山东济南地区年太阳辐射量数据图
复杂受光下的光伏阵列的输出曲线,即和曲线如图5 所示。当三组光伏模块倾角均为最佳倾角(30 度),即相应的光照强度G=G=G=1472W/m,输出特性曲线如“date1”所示,可见当三组光伏模块受到的光照强度一致时,输出曲线和输出曲线和图2一致,其中输出曲线为单峰值状态。

图5 复杂受光下光伏阵列I-V和P-V输出特性曲线
当三组光伏模块对应的倾角分别为0 度,30 度和90 度,相应的光照强度G=1334W/m,G=1472W/m,G=957W/m时,光伏阵列的输出曲线即,输出曲线如“date2”所示。
从“date1”与“date2”的对比可知,当串联光伏阵列在复杂受光条件下时,光伏阵列的电气输出特性曲线会发生显著变化,由曲线的对比可知,当光伏阵列在复杂受光条件下,曲线呈现“阶梯”形状。从曲线中可知,当光伏阵列在复杂受光条件下,光伏阵列的输出功率呈现多峰值现象,即光伏阵列的复杂多峰现象。并且曲线对比可以看出,当光伏阵列在复杂受光条件下,光伏阵列的输出功率会比均匀光照强度低,相应的多峰值的最大功率点功率也比单峰值的最大功率点功率低,并且光伏阵列受光条件越复杂,光伏阵列的最大功率点就越低,因此,它将影响整个光伏阵列的发电效率。并且由于复杂受光下光伏阵列的曲线的多峰特性输出现象,致使传统的MPPT 算法无法正常使用,该现象为后续MPPT 算法奠定了理论基础。
3 结束语
本文基于光伏电池单二极管模型进行建模仿真研究,在均匀光照下光伏电池电气输出特性数学模型的基础上,推导出复杂受光条件下串联光伏阵列的电气输出特性数学模型,并对数学模型进行理论分析,利用Matlab/Simulink 软件建模仿真研究其电气输出特性。通过研究串联光伏阵列分别在均匀光照和复杂光照下的电气输出特性曲线可知,当串联光伏阵列在复杂受光条件下,光伏阵列电气输出特性曲线会产生较大变化,功率输出曲线会出现多个峰值点,得出了传统的MPPT 算法已经无法正常使用,MPPT 算法有待改进的结论,在光伏系统的建设中,为光伏阵列设计时采用能避免陷入局部最大值的最大功率点技术提供依据;并且从功率输出曲线对比分析可知,串联光伏阵列在复杂受光条件下的最大功率点比均匀光照下的最大功率点明显降低,因此,得出复杂受光条件对光伏系统发电量影响较大的结论。

