基于混沌莱维萤火虫算法的钢筋智能生产调度与控制*

黄志祥，何玮明，陆权丰

(1.广西大学 土木建筑工程学院，广西 南宁 530004；2.广西建工积健建材制造有限公司，广西 南宁 530000；3.广西建工智慧制造研究院有限公司，广西 南宁 530000)

0 引言

随着科学技术与信息技术的不断发展，钢铁行业的竞争也越发激烈.为了能更好适应钢铁行业的发展，使企业在行业中占据一席之地，各大钢铁企业积极推进钢铁生产线改造，力求获得一个集智能、集成与柔性特征于一身的智能化生产线[1-2].

柔性生产线由于具备满足并行制造需求与高生产效率的双重优点，近年来被各行各业纷纷采用.通过合理且高效的生产线调度与控制管理可使企业在低能耗的条件下便能高效率、高质量地完成生产任务.因此，合理调度与控制管理生产线从长远看对企业的发展具有非常重要的意义[3-4].

在成型钢筋智能生产过程中经常会发生生产线拥堵以及生产线饥饿等状况，长此以往，对企业的发展非常不利.为此，国内外诸多学者针对智能生产线调度控制过程中存在的问题进行了大量研究，力求获得一种高效合理的智能生产线调度控制方法，从而为生产线的安全稳定运行提供可靠保障.研究中比较受欢迎的有潘志豪等[5]研究的基于混合优化算法的生产线平衡控制方法、李静等[6]人研究的基于混合流水生产线的生产线分批调度方法.二者的研究均一定程度上改善了智能生产线调度控制过程中出现的生产线拥堵以及饥饿等问题，使得生产线的生产效率得到了一定程度提升.但是由于多约束求解过程是一个非常复杂的过程，上述两种方法在计算的准确度以及计算效率方面并不能很好满足当前钢铁企业对智能化生产线进行最优调度的需求.

莱维萤火虫算法隶属智能优化算法范畴，常被应用于各种生产线调度优化问题的求解中，不仅能够最大限度接近生产线优化调度模型的最优解，在计算准确性与效率方面优势也非常明显[7].为此，本文提出基于混沌莱维萤火虫算法的钢筋智能生产调度与控制方法，有效解决成型钢筋智能生产过程中存在的问题，提升成型钢筋的生产效率.

1 钢筋智能生产调度与控制

1.1 智能生产调度与控制问题

1.1.1 问题介绍钢筋智能生产调度与控制问题的实质是以实现企业效益最大化为目标，对生产资源实施合理分配的过程.通常情况下，评价调度与控制方法的优劣主要是看其在降低生产成本以及提高生产效率方面是否具有优势，具体来讲就是看其是否能尽量降低成型钢筋的库存量、提高钢筋制造设备的利用率、使完工时间尽量最短等[8].

在实际的钢筋智能生产调度与控制问题中，必须对全部的物流智能机器人运动路线、所有制造单元各不相同的成型钢筋加工时间以及成型钢筋的输送时间进行全面而综合的考虑，才能最大限度地避免智能生产线出现阻塞或饥饿的状况，从而保证智能生产线安全稳定地运行.

1.1.2 钢筋智能生产调度与控制过程分析一般情况下，钢筋智能生产过程是由调度控制中心、装卸载、物流运输以及一些执行和辅助模块组成的[9].钢筋智能生成线的准备工作在装载区进行，准备工作完成后，调度控制中心会向物流运输智能机器人发布指令，指挥物流运输智能机器人将待加工工件运输到各加工位置，此时加工区域的智能设备会按照相关指令完成成型钢筋工件的加工，加工完毕的成型钢筋工件到达后处理区后，再由物流智能机器人将成型钢筋工件输送到下一个工序的加工位置，待所有加工工序完毕后，将其输送到物流中心卸载区域，便可完成整个钢筋智能生产过程的调度与控制.

1.1.3 智能生产调度控制原则为了使钢筋智能生产调度与控制过程中尽量不出现智能机器设备碰撞以及成型钢筋加工设备故障，应保障整个调度控制过程的稳定运行[10].在调度控制时应遵循如下原则：

①每个智能机器人一次只能运送一个成型钢筋工件到加工位置.

②物流中心要拥有足够大的存储空间放置成型钢筋工件与一些成型钢筋生产物料.

③完成一个成型钢筋工件的加工后，下一个待加工成型钢筋工件能够被自动输送到加工位置.

④不考虑成型钢筋工件大小对工件装卸以及运输时间上造成的影响.

1.2 钢筋智能生产调度与控制模型构建

1.2.1 设计目标函数企业的差异使得企业对待智能生产线的调度与控制有着不一样的需求与评价标准，但是多数企业都会将目标函数作为企业智能生产调度与控制效果优劣的最可靠依据[11].本文主要将最少调度时间作为优化目标函数.

假设f代表目标函数，其用公式可表述为：

fz=min{max[Qk(oi)]},1≤i≤n,1≤l≤5，

(1)

式中：成型钢筋的工件数与工序数分别用i与l代表；整个调度控制过程花费的时间用Qk(oi)代表.

1.2.2 设置目标函数约束条件本文将以下三个约束作为成型钢筋智能生产调度与控制模型目标函数的约束条件.

约束条件1：第一道成型钢筋工序花费时间Q1(oi).也就是物流运输智能机器人将待加工工件首次运输到首工序加工位置与在装载区等待智能机器人的时间.

Q1(oi)≥mov(B1,oi1)+add(oi1)，

(2)

式中：物流运输智能机器人将待加工工件首次运输到首工序加工位置的时间用mov(B1,oi1)代表；物流装载区域用B1代表；add(oi1)代表在装载区等待智能机器人的时间.

约束条件2：成型钢筋工件加工处理时间Q2(oij).也就是对成型钢筋工件加工的时间.

Q2(oij)≥M(oij)，

(3)

式中：成型钢筋工件i在第j个工序的加工时间用M(oij)代表.

约束条件3：最后一道成型钢筋工序花费时间Q3(oi).也就是待所有工序完成之后等待智能机器人的时间与将其输送到物流中心卸载区域的时间.

Q3(oi)≥mov(oij,B2)+add(oi3)，

(4)

式中：mov(oij,B2)代表将成型钢筋工件运回物流中心卸载区域的时间；add(oi3)代表所有工序完成之后等待智能机器人的时间.

1.3 混沌莱维萤火虫算法

1.3.1 萤火虫算法简介萤火虫算法是一种以萤火虫为模仿对象，通过模仿萤火虫发光现象对优化问题进行求解的仿生算法.它的提出对于解决优化调度问题意义重大[12].

在实际生活中，我们可以发现，我们与光源之间的距离与光的亮度呈负相关，当我们距离光源很远时，光的亮度会很弱或者看不见.同理，萤火虫发出的光也仅在有限的范围内能够被另一些萤火虫看到.因而在萤火虫算法中，有如下假设：

① 各个萤火虫之间都可以实现互相吸引，不存在像人一样的性别之分.

② 在萤火虫算法中，吸引力与光的亮度正相关，也就是说，哪只萤火虫发出的光更亮，相对来说就更具有吸引力.通俗点说，就是在飞行的过程中，亮度大的萤火虫会因为具有更亮的亮度将亮度小的萤火虫吸引到自己这里来.在萤火虫群体中拥有最大亮度的萤火虫可以进行随机飞行[13].

③ 要根据要解决的问题合理设置萤火虫的亮度值.每个萤火虫在某一个位置的亮度值是固定不变的.这个变量受要解决问题的制约.

1.3.2标准萤火虫算法在标准萤火虫算法中，将钢筋智能生产调度与控制模型的解视为一组飞行中的萤火虫，那些亮度较大的萤火虫所在的位置被看成最优解，因为相互吸引的作用，所有的萤火虫会不断地靠近拥有最优位置的萤火虫[14].

用i与j分别代表两只萤火虫，两只萤火虫之间的绝对亮度用Hij代表，用g代表变化距离，Hij随g的变化过程用公式可表示为：

(5)

式中：萤火虫j在g=0条件下的光强度用Hj代表；γ代表一个参数，吸引力的变化要受到γ的制约，通常状况下γ满足0.01≤γ≤100.用公式(6)将两只萤火虫的吸引力描述为：

(6)

式中：萤火虫在最大荧光处的吸引度用θ0代表；两只萤火虫在xi与xj之间的笛卡尔距离用gij代表.那么这个笛卡尔距离用公式可表示为：

(7)

式中：维数用d代表；第i个萤火虫在第k维度的空间坐标用xi,k代表，在钢筋智能生产调度与控制过程中，亮度更强的萤火虫j对萤火虫i的吸引运动过程可表示为：

xi(t+1)=xi(t)+θij(gij)(xj(t)-xi(t))+α(g1-0.5)xM，

(8)

式中：萤火虫当前位置的影响用xi(t)表示，它对全局与局部搜索能力的平衡具有非常重要的作用；萤火虫之间的吸引力用θij(gij)(xj(t)-xi(t))反映；α(g1-0.5)xM中的随机步长可起到提高全局最优能力的目的.调度与控制模型目标函数在搜索空间的上下限差值用xM表示.

1.3.3混沌莱维萤火虫算法根据标准萤火虫算法的相关描述，在解决优化问题的初期，萤火虫一般会呈现较为分散的分布状态，原因是萤火虫在此时彼此相距的距离较远，吸引力也就相对较小[15].那么一旦出现优化问题求解范围过大的状况，很难完成求解.因而本文对标准萤火虫算法进行以下两个方面的改进：

为了防止由于萤火虫之间吸引力过小，而导致的优化问题求解困难状况的发生，通过提高萤火虫算法优化问题求解初始阶段收敛速度，加强萤火虫之间吸引力的方式对标准萤火虫算法的吸引项加以改进.具体的做法是应用混沌优化算法对吸引系数γ进行吸引优化，以动态的方式对吸引系数γ执行合理且有效的取值操作.用公式可将其表达为：

γk+1=uγk(1-γk)，

(9)

式中：迭代次数用k代表；混沌因子用u代表.

随机过程选择是保证局部搜索行为能否安全有效进行的关键因素.基于此，本文根据启发式方法中的描述，采用LevyFlight作为新步长方式，完成对随机项的改进.经过上述改进，混沌莱维萤火虫算法的更新过程可用公式描述为：

xi(t+1)=xi(t)+θij(gij)(xj(t)-xi(t))+α(g1-0.5)⊕Levy·xM，

(10)

式中：Levy随机搜索路径用Levy代表；点对点乘法用⊕代表；需要注意的是随机步长要按照莱维分布进行设置.

Levy随机步长的求解过程用公式可表述为：

Levy:s=t-λ,λ∈(1,3]

(11)

通过对基本萤火虫算法吸引项与随机项的改进，可以为钢筋智能生产调度与控制过程提供一个较为优越的初始搜索环境，从而有效发挥萤火虫算法在模型求解方面的优势.具体的模型求解过程如图1所示.

2 实验与分析

实验以某大型钢厂的成型钢筋智能生产线为实验对象，利用matlab软件模拟该生产线的调度控制过程，以验证本文方法的有效性.

为验证本文方法的应用优势，应用本文方法对生产线的四种分布进行优化调度与控制.成型钢筋智能生产线的四种分布形式如图2.每种分布形式均包括6个执行模块(N1～N6)，装载与卸载站用(Z/X)表示.分别应用标准萤火虫算法与混沌莱维萤火虫算法对钢筋智能生产调度与控制模型进行150次的求解，求解结果如表1.

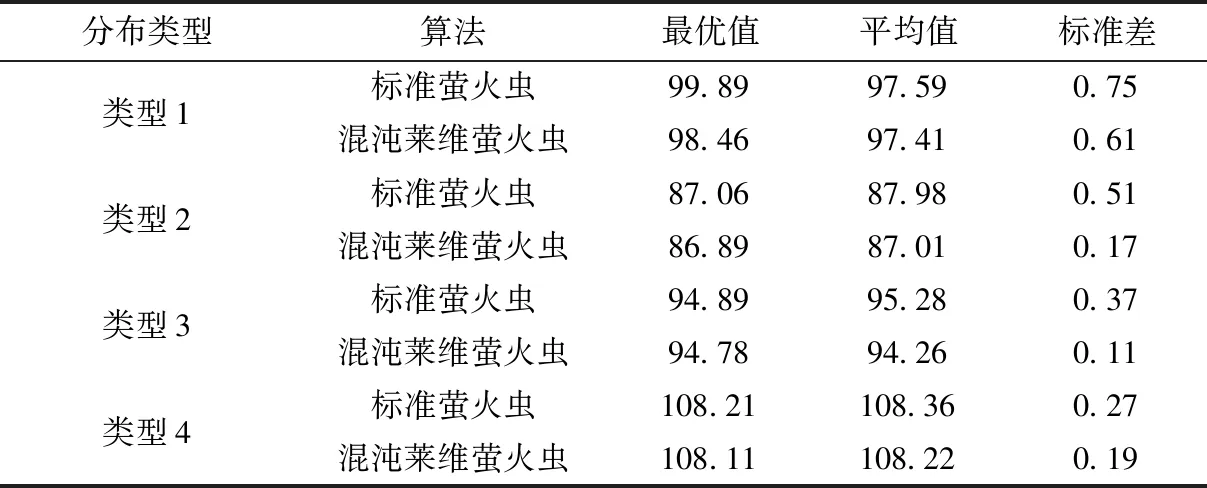
表1 两种算法模型求解结果Tab.1 Solving results of two algorithm models

从表1可以看出，4种分布类型中分布类型2的最优值与平均值最低，用时最短.分布类型4的最优值与平均值最高，用时最多.并且无论是对哪种分布类型智能生产线进行调度，应用混沌莱维萤火虫算法得到的标准差的值都要低于应用标准萤火虫算法对调度模型求解获得的标准差的值.说明应用本文方法可以有效实现对成型钢筋智能生产的调度控制，在模型求解过程中具有较好的准确性与稳定性.

图3统计的是应用本文方法与文献[5]方法、文献[6]方法进行生产调度控制后每小时生产的成型钢筋产量.

分析图3可知，应用本文方法对成型钢筋智能生产线进行调度控制后每小时成型钢筋的产量始终高于文献[5]、文献[6]方法.四次实验中，应用本文方法进行成型钢筋智能生产线调度控制后成型钢筋的产量都很高，趋势也比较稳定.而应用其他两种方法后成型钢筋的产量并不稳定.这说明，本文方法在提高成型钢筋的生产效率上更具优势，稳定性也更强.从长远看，本文方法更适合用于对成型钢筋智能生产线进行调度与控制.

为验证本文方法在求解模型时的收敛性能，绘制应用标准萤火虫算法与混沌莱维萤火虫算法对模型求解时的收敛效果图如图4.

从图4可以看出，应用混沌莱维萤火虫算法在对模型目标函数求解时，在迭代次数约为30次时，便达到了收敛状态，而应用标准萤火虫算法对模型目标函数求解时，则在迭代次数约为60次时，才达到收敛状态.实验证明：应用本文方法后，模型的目标函数收敛速度更快，具有较好的运算性能，将其应用于成型钢筋智能生产线调度中可有效提升调度效率.

图5显示的是分别应用本文方法与文献[5]、文献[6]方法对钢筋智能生产调度与控制模型求解获得的最优效果分布图.

从图5显示的最优效果分布对比图可以看出，应用本文方法获得的最优目标函数值始终低于其他两种方法，并且从总体趋势上看，本文方法的最优分布曲线趋势较为平稳，而其他两种方法的最优分布曲线波动幅度相对较大.这说明，本文方法的优化效果要高于其余两种方法，求解精度以及稳定性都很强，可跳出局部最优，寻找到全局最优解.

3 结论

本文方法可以实现对成型钢筋智能生产的调度与控制，应用效果较好，其具有如下优势：

1)应用混沌莱维萤火虫算法求解到的模型标准差的值无论在哪种智能生产线分布类型下均低于应用标准萤火虫算法对模型求解获得的标准差的值.这说明本文方法不仅可以用于解决成型钢筋智能生产线优化问题，并且在对模型的求解过程中具有较好的准确性与稳定性，可更好满足实际钢筋智能生产工作的需要.

2)应用本文方法后，成型钢筋的产量高，趋势也比较稳定，并且应用本文方法只需要较少的迭代次数就可寻求到模型的最优解，在解决成型钢筋生产线调度问题上更具优势.