基于自适应粒子—蚁群算法的掘进面机器人装药路径智能优化
蒋浩辰,查正清,段 云
(1.北京矿冶研究总院,北京 100160;2.矿冶科技集团有限公司,北京 100160)
目前地下矿山开采存在自动化及智能化程度较低、工人的作业环境较差、开采效率较低等问题。为保障作业人员安全,将工业机器人用于地下矿山掘进面的对孔装药作业中,而地下矿山掘进面对孔装药效率在一定程度上影响开采效率。装药路径规划问题可简化为TSP问题,常被用于TSP问题求解的智能优化算法包括遗传算法、粒子群算法、蚁群算法等。
20世纪90年代,意大利学者MARCO DORIGO[1]首次提出蚁群算法(Ant Colony Optimization,ACO)的基本模型,并将其用于TSP求解。1996年,MARCO DORIGO等[2]发表文章详述蚁群优化算法的理论基础及数学模型。
经过近三十年的研究,蚁群优化算法已被广泛用于TSP问题求解、机器人路径规划、控制系统参数优化等领域。蚁群优化算法应用范围广泛,但存在参数多且不易确定、求解效率低、易收敛到局部最优解等缺点。国内外学者针对基本蚁群优化算法存在的缺点提出大量改进策略,并取得丰硕研究成果。
文献[3-6]对信息素浓度的更新策略进行改进,算法的收敛速度与精度得到提升;文献[7-8]通过对蚁群算法中的三个参数α、β和ρ优化求解,提升蚁群算法求解性能;文献[9]在ACS基础上加入一个伪随机因子,通过调节该因子平衡算法前期及后期的搜索能力与收敛速度,并引入精英蚂蚁,算法收敛速度与多样性得到提高。文献[10]将蚁群算法与禁忌搜索算法相结合作为局部搜索解决TSP问题,利用一个存储结构来记录已搜索局部路径,防止搜索到的局部路径在解集空间中再次被搜索,改进算法具有较好的全局搜索能力。
为避免因参数选取不当导致算法性能较差的情况,提高蚁群优化算法收敛速度的同时避免算法过早收敛于局部最优解的现象,对基本蚁群算法做如下改进:将粒子群算法用于蚁群算法的参数求解,通过改进粒子群算法的惯性权重、蚁群算法中引入自适应信息素挥发因子ρ、改进信息素浓度更新策略,使算法具有更强的全局搜索能力,提升算法求解性能。最后以TSPLIB测试库中部分问题为测试对象,将本文改进算法、基本蚁群算法以及最大最小蚁群算法分别用于求解问题,并比较求解结果以证明改进算法的求解性能。
1 基于粒子群算法求解蚁群算法参数
参数选取影响蚁群优化算法求解性能,蚁群算法参数中,信息素启发式因子α和期望值启发因子β是一对关联性很强的参数:蚁群算法的全局寻优性能,要求蚁群的搜索过程具有较强的随机性;蚁群算法的快速收敛性能,要求蚁群的搜索过程具有较高的确定性。两参数对蚁群算法性能的影响和作用是相互配合、密切相关的,算法要获得最优解,就必须在这二者之间选取一个平衡点,才能避免在搜索过程中出现过早停滞或陷入局部最优等情况。
1.1 粒子群算法求解蚁群算法参数过程
粒子群算法是通过模仿鸟群觅食行为而提出的,其具有模型简单、收敛速度快、设置参数少、容易与其它算法融合使用等特点,可以对蚁群算法的参数进行优化。因此本文采用粒子群算法求解蚁群算法中的信息素启发因子α、期望值启发因子β。
粒子群算法求解蚁群算法参数的基本思想为:随机生成N个粒子,每个粒子在空间中对应一个二维坐标,坐标中两个值分别对应蚁群算法中的α、β两个参数;将每个粒子的二维坐标反馈给蚁群算法,并用基于这组参数的蚁群算法求解TSP,所求得的最短路径长度作为粒子群算法的目标函数;粒子群算法根据目标函数求出个体最优解Pbest和群体最优解Gbest,并依据Pbest和Gbest更新粒子的位置与速度;为提高粒子群算法的收敛速度,需确定合适的粒子运动范围和最大速度;最终所有粒子飞向同一个点,该点的坐标即为蚁群算法参数。粒子群算法求解蚁群算法参数流程图如图1所示。

图1 粒子群算法求解蚁群算法参数流程图Fig.1 Particle swarm optimization algorithm to solve ant colony algorithm parameter flow chart
粒子群算法求解蚁群算法参数的具体步骤如下。
步骤1:设计粒子群参数,国内外学者通过反复实验发现蚁群算法参数α的最佳取值范围为[1,2],β的最佳取值范围为[4,9],两个参数取值范围对应粒子位置坐标的取值范围,粒子速度的取值范围设为位置范围的十分之一。随机生成N个二维粒子X1,X2,…,Xn。
步骤2:将每个粒子的坐标作为蚁群算法一组参数,用基于这组参数的蚁群算法求解TSP问题。
步骤3:将所得路径长度作为目标函数,根据目标函数更新个体最优解Pbest和群体最优解Gbest。
步骤4:根据式(1)和式(2)更新粒子的速度和位置[12]。
Vi(t+1)=ωVi(t)+C1r1(Pbesti(t)-Xi(t))+C2r2(Gbesti(t)-Xi(t))
(1)
Xi(t+1)=Xi(t)+Vi(t+1)
(2)
式中:ω为粒子运动惯性权重;r1、r2为[0,1]区间的随机数;t为当前迭代次数;Pbesti(t)为当前迭代中粒子个体的最优位置;Gbesti(t)为当前迭代中粒子全局的最优位置;Vi(t)为当前迭代中粒子运动速度;Xi(t)为当前迭代中粒子位置;C1、C2为常数。
1.2 粒子群算法改进
粒子群速度更新公式中,ω为非负数,其表示前一时刻粒子运动速度对后一时刻运动速度的影响程度。当ω取较大值时,后一时刻运动速度受前一时刻运动速度影响较大,算法具有较强的全局搜索能力;ω取值较小时,后一时刻运动速度受前一时刻运动速度影响较小,算法具有较强的局部搜索能力。通过调整ω值大小可使算法跳出局部最优解。
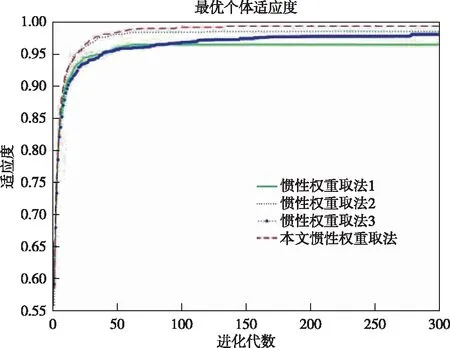
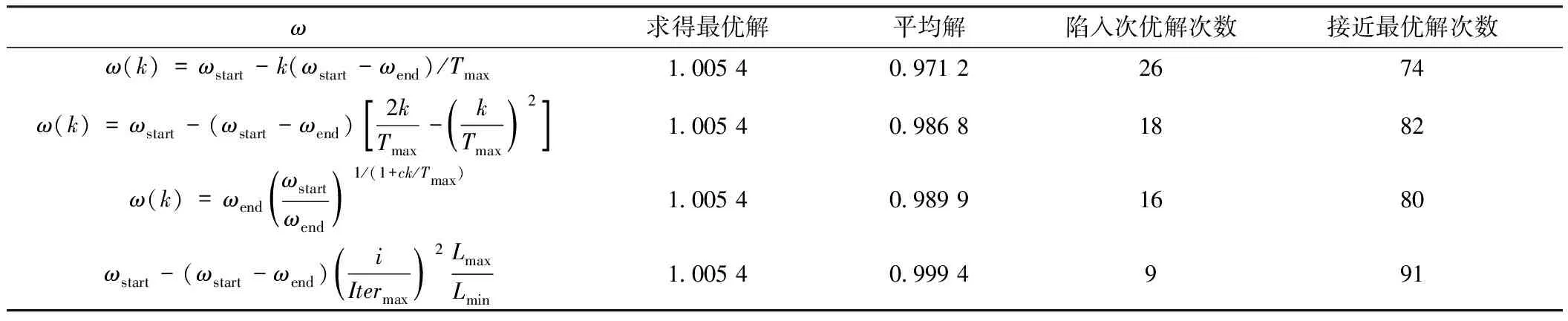
史峰等[11]对具有自适应变化ω的粒子群算法性能进行分析,提出4种不同ω取值方法并对多组函数求解,比较所得解的平均值、陷入次优解次数及求得最优解的次数。分析可知,惯性权重ω取为常数时,粒子群算法具有较快的收敛速度,但算法后期易因收敛到局部最优解而停滞;采用ω自适应变化时,算法前期收敛速度较慢,但全局搜索能力较强,求解精度较高。
本文采用式(3)计算动态变化ω惯性权重。
(3)
式中:i为当前迭代次数;ωstart为初始惯性权重;ωend为最终惯性权重,一般取ωstart=0.9,ωend=0.4;Itermax为最大迭代次数;Lmax为本次迭代最长路径长度;Lmin为本次迭代最短路径长度。
本文中给出的动态变化ω惯性权重具有以下特点:
1)将权重值的取值范围设定在[0.4,0.9],使上一时刻速度对当前速度影响适中。
2)算法在循环迭代初期,粒子以较高的速度运动,算法更容易搜索到全局最优解所在区域;随着算法循环迭代次数增加,逐渐降低粒子运动速度,算法的局部搜索能力逐渐增强,易于搜索到全局最优解。
3)将蚁群算法本次循环搜索到的最短路径长度及最长路径长度与ω惯性权重关联,当最短路径长度越小于最长路径长度时,表示粒子越接近最优解,此时降低粒子运动速度,提高算法局部搜索能力。
1.3 蚁群算法改进
1.3.1 信息素挥发因子ρ
信息素挥发因子ρ可以影响蚁群算法的随机搜索能力,在传统蚁群算法中,ρ一般取为固定常数[12]。针对TSP求解,应使算法在循环迭代初期具有更强的全局搜索能力,以获得更多不同的可能解;随着循环迭代次数增加,算法的局部搜索能力应逐渐增强,以寻得最优解。
本文采用自适应变化信息素挥发因子ρ,当蚁群算法的迭代次数小于指定值,ρ的更新方式如式(4)所示。
ρ(NC+1)=
(4)
式中:NC为当前迭代次数;NCset为设置的迭代次数;Iterbest为最优解从初次求得至当前未更新次数;Iterset为设置的最优解未更新次数;ρmax为最大信息素挥发因子;ρmin为最小信息素挥发因子。
本文的信息素挥发因子具有以下特点:
1)取值存在上下限,使信息素挥发速度适中。
2)在算法迭代初期,信息素挥发较快,蚁群随机搜索能力较强,算法全局搜索能力得到提高;在算法迭代后期,信息素挥发较慢,蚁群随机搜索能力较弱,算法局部搜索能力得到提高。
3)算法长时间内未发现更优解时,适当增加信息素挥发速度,提高算法全局搜索能力。
1.3.2 信息素浓度更新策略
信息素浓度更新策略包括定值变化与自适应变化,大部分学者在对信息素浓度自适应变化时,只考虑每次迭代后求得数值解是否更优,而未对问题的几何特性加以约束[13-15]。本文以TSP为背景,搜索路径长度最短的轨迹。以图2中的A、B、C、D四个城市为例,由三角形两边之和大于第三边定理可知:
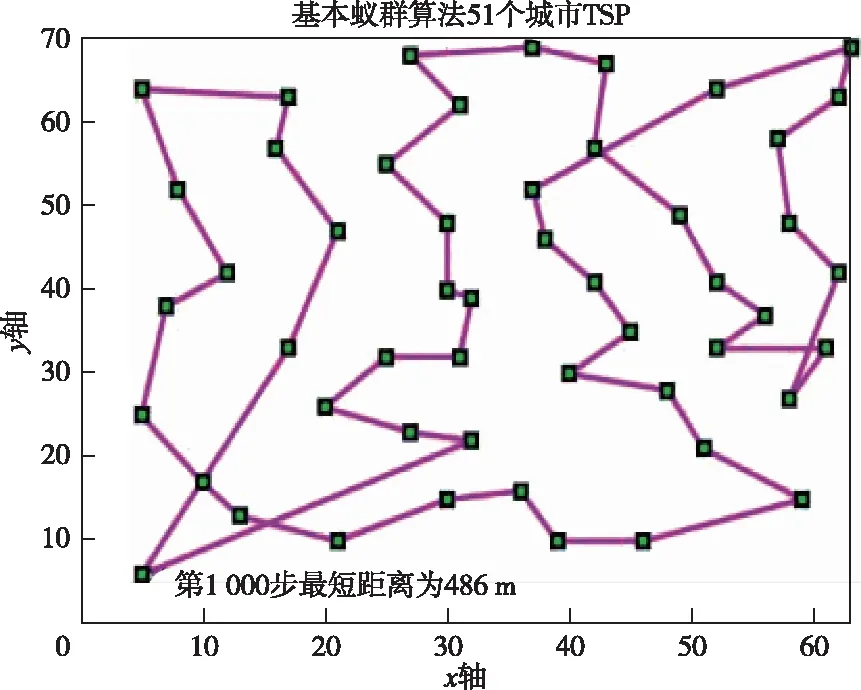
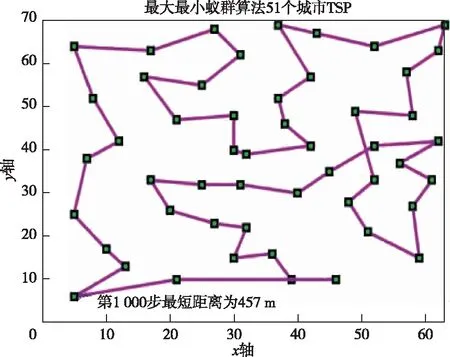
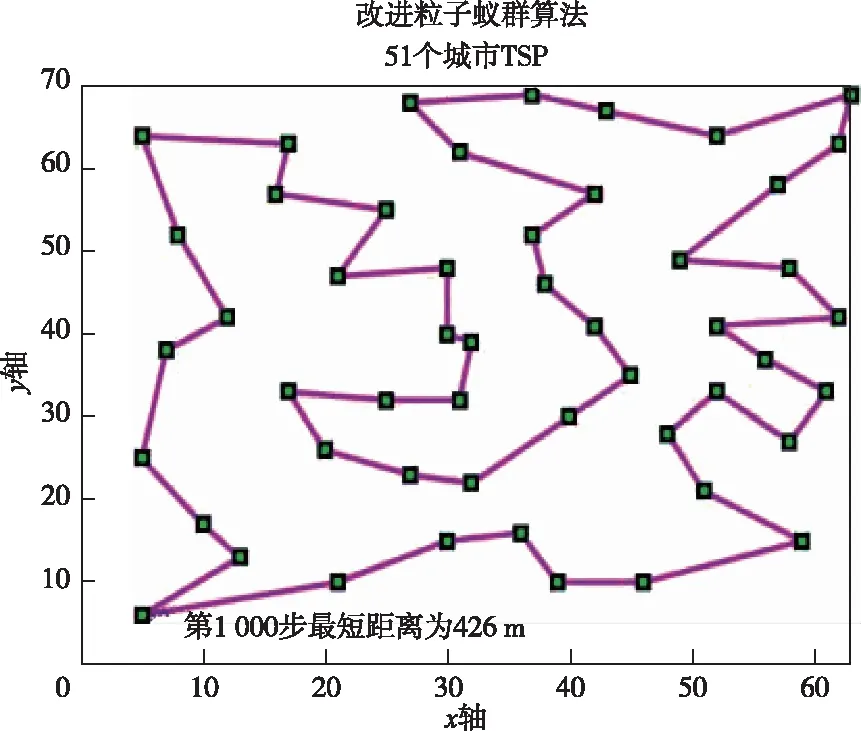
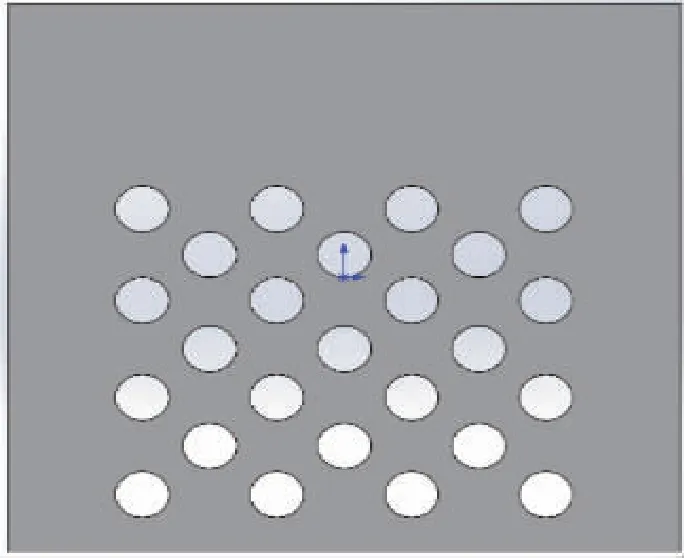
DC+AB (5) AD+BC (6) 图2 四座城市间所有可能路径Fig.2 All possible routes between the four cities 本文信息素浓度更新策略如下: 1)当NC τij(NC+1)=(1-ρ)τij(NC)+Δτij(NC, NC+1) (7) 式中:τij为路径ij上的信息素浓度。 2)当NC>NCset,Iterbest≥Iterset且局部路径不相交时: (8) 式中:τmax为最大信息素浓度;k为常数,通过实验,本文取k=5。 3)NC>NCset,Iterbest≥Iterset且局部路径相交时: τij(NC+1)=τmin (9) 式中:τmin为最小信息素浓度。 本文用于测试算法的非线性函数为式(10),目标为求取函数在自变量[-2,2]间的极大值,函数图形如图3所示。 (10) 图3 函数图形Fig.3 Function graph 公式(11)至(13)为常用的惯性权重。 ω(k)=ωstart-k(ωstart-ωend)/Tmax (11) (12) (13) 利用公式(11)至(13)及本文提出的公式(3)表示的惯性权重粒子群算法对非线性函数公式(10)求解,算法适应度变化曲线如图4所示,ω动态变化曲线如图5所示。 图4 适应度变化曲线Fig.4 Fitness change curve 图5 ω动态变化曲线Fig.5 ω dynamic curve 粒子群算法参数设置:粒子个数m=20,迭代次数N=300。每种不同ω取值方法运行100次,并比较所得解的平均值、陷入次优解次数和接近最优解次数,分析其收敛精度和收敛速度等性能。已知函数最优解为1.005 4,将大于0.847 7小于等于1.005 4的解视为接近最优解,将0.847 7及更小的解视为陷入局部最优的解。实验结果如表1所示。 表 1 4种惯性权重下的算法性能比较 分析图4及表1可知,本文提出的惯性权重动态变化方法在前期变化较慢,取值较大,算法具有较强的全局搜索能力;后期惯性权重动态变化较快,算法具有较强的局部搜索能力,且算法收敛速度更快,获得较好的求解结果。 本文对蚁群算法的信息素挥发因子和信息素浓度更新策略进行改进,为验证参数改进对粒子蚁群算法性能的影响,基于MATLAB平台,选取TSPLIB测试库中的Oliver30、Eil51、Att48、Eil76作为测试数据,分别用基本蚁群算法、粒子蚁群算法、最大最小蚁群算法、信息素挥发因子动态变化粒子蚁群算法、改进信息素浓度更新粒子蚁群算法以及本文所提的改进粒子蚁群算法求解50次,最大迭代次数均为1 000次,并分析求解结果,求解结果如表2至表5所示。 表2 Oliver30问题求解结果 表3 Eil51问题求解结果 表4 Att48问题求解结果 表5 Eil76问题求解结果 已知Oliver30整数最优解为420,Eil51整数最优解为426,Att48整数最优解为33 522,Eil76整数最优解为538。 由求解结果可知基本蚁群算法及粒子蚁群算法在对4种问题的50次求解中均未求得最优解,最大最小蚁群算法仅在一种问题的50次求解中求得最优解,而本文提出的改进粒子蚁群算法在4种问题求解中均至少求得一次最优解,最差解优于其他几种算法,平均求解精度较其他几种算法高5%~9%。本文提出的基于动态变化信息素挥发因子和信息素浓度更新策略蚁群算法在TSP问题求解上具有较好性能。 以Eil51问题为例,三种算法求解的平均距离和最短距离变化曲线如图6至图11所示。 图6 基本蚁群算法求得路径Fig.6 Path planning by ACO 图7 基本蚁群算法求得平均距离与最短距离Fig.7 The average distance and minimum distance of path planning based on ACO 图8 最大最小蚁群算法求得路径Fig.8 Path planning by MMAS 图9 最大最小蚁群算法求得平均距离与最短距离Fig.9 The average distance and minimum distance of path planning based on MMAS 图10 改进粒子蚁群算法求得路径Fig.10 Path planning by improved PSO-ACO 图11 改进粒子蚁群算法求得平均距离与最短距离Fig.11 The average distance and minimum distance of path planning based on improved PSO-ACO 通过分析可知,基本蚁群算法与最大最小蚁群算法求得的最优路径中,均出现局部路径交叉情况,没能搜索到全局最优解,且算法在200次迭代内迅速收敛于局部最优解;改进粒子蚁群算法求得的最优解路径中,没出现局部路径交叉情况,信息素浓度自适应调整,算法在后期能跳出局部最优解,搜索到全局最优解,缺点是收敛速度较慢。 为验证本文设计装药路径规划算法对机器人掘进面对孔装药效率的影响,在实验室中搭建模拟掘进面对孔环境,实验环境如图12所示。 图12 实验环境Fig.12 Experimental environment 模拟掘进面模型如图13所示,模拟炮眼分布如图14所示。分别利用基本蚁群算法与改进粒子—蚁群算法对模拟掘进面炮眼装药路径进行规划,路径规划结果分别如图15、16所示。对孔路径总长及对孔耗时如表6所示。 图13 模拟掘进面建模Fig.13 Modeling of simulated driving face 图14 模拟炮眼分布图Fig.14 Simulated borehole distribution map 图15 基于基本蚁群算法规划装药路径Fig.15 Charge path planning based on basic ant colony algorithm 图16 基于自适应粒子—蚁群算法规划装药路径Fig.16 Charging path planning based on adaptive particle ant colony algorithm 表6 对孔实验结果 由实验结果可知,针对实验中模拟掘进面炮眼对孔路径规划,机器人根据蚁群算法规划的装药路径装药总时长79.1 s,根据本文提出算法规划装药路径装药总时长72.6 s,采用本文改进算法所规划的装药路径较基本蚁群算法缩短约8%。利用本文改进粒子—蚁群算法规划所得装药路径总长更短,机器人对孔效率得到提升。 本文针对地下矿山掘进面对孔装药路径规划问题,利用粒子群算法优化蚁群算法中的部分参数,提出一种基于参数自适应调整惯性权重及一种基于判断局部路径是否交叉自适应更新信息素策略。仿真结果证明改进算法具有较强的全局搜索能力与局部搜索能力,求解精度高于基本蚁群算法、最大最小蚁群算法及粒子蚁群算法等算法,规划的对孔装药路径更优,提升了地下矿山开采效率。
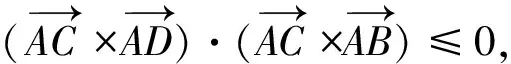
2 仿真实验及结果分析
2.1 粒子群算法惯性权重改进性能分析


2.2 本文改进粒子蚁群算法求解性能分析







2.3 模拟对孔实验





3 结论

