一维螺旋型Se 原子链中的Rashba 效应和平带性质
孙海明
(湖南师范大学物理与电子科学学院,长沙 410081)
探索低维体系电子态的调控规律可以为构筑下一代微纳电子学器件提供理论基础.本文采用第一性原理计算研究了一维螺旋型Se 原子链的结构性质和电子性质.结果发现,该结构比直线型结构能量要低得多,且具有动力学和热力学稳定性.能带计算表明,这种螺旋型一维原子链结构是带隙约为2.0 eV 的半导体,且在X 点附近展现出Rashba 型的自旋劈裂.这种特殊的原子链结构便于人们通过应力调控其电子性质.计算结果表明,5%的拉伸应变就可以将其带隙减小20%,而5%的压缩应变将Rashba 能量偏移增大到平衡体积时的2 倍多.此外,其价带是一条平带,引入空穴掺杂可以诱导产生磁性,从而使体系转变为半金属.进一步增加空穴掺杂,体系转变为铁磁金属.同样,这种掺杂效应还出现在一维螺旋型Te 原子链中.
1 引言
Rashba 效应是指在晶体表面由于中心反演对称性破缺引起的能带自旋-轨道劈裂[1].对于电场中的二维电子气,其有效哈密顿量通常可以写成H︿R=λσ·(Ez×k),其中,σ为泡利自旋算符,k 为表征电子态的波矢,Ez为垂直于电子气所在平面的外电场,λ代表自旋-轨道耦合(spin-orbit coupling,SOC)强度.由此,电子能级会产生正比于k的劈裂,即ΔE(k)=αRk,αR被称为Rashba 参数,包含了SOC 强度和电场强度.因此,调节αR可以调控Rashba自旋劈裂,进而调控电子自旋极化,为实现电场操控自旋、构筑自旋场效应晶体管提供理论基础[2].此外,Rashba 效应也是人们实现晶体中自旋霍尔效应、Majorana 费米子等新奇物理现象和量子态的基础[3,4].
过去的二十多年里,Rashba 效应的研究主要集中在重元素金属表面和界面结构[5−14].例如,人们最早通过角分辨光电子谱实验在Au 表面直接观测到有自旋劈裂的能带[5].之后,Ast 等[7]在Ag(111)面有序掺杂1/3 层的Bi 原子后观测到高达200 meV 的Rashba 能量偏移[7](正文中定义为ER),比在Au 表面观测到的Rashba 能量偏移(约2.1 meV)大2 个数量级,比Bi 表面的Rashba劈裂(约14 meV)大1 个数量级;其Rashba 参数αR达到3.0 eV·Å (1 Å=10–10m),比Au(111)面的0.33 eV·Å大1 个数量级.此外,Ishizaka 等[15]在具有无中心反演对称的极性晶体BiTeI 中也观测到了巨大的Rashba 效应,其Rashba 参数更大,达到3.8 eV·Å.最近有理论预言,通过对Bi 单层进行有序合金并采用极性衬底,可以显著增强表面单层中的Rashba 劈裂;其中SbBi/Al2O3(0001)和PbBi/Al2O3(0001)的Rashba 劈裂分别高达640,740 meV,αR则分别达到3.55,4.38 eV·Å[16].在铁电体中,还可以实现Rashba 效应的铁电调控,即通过外电场调控实现非易失性自旋极化翻转[17−19].
以上研究的大多是二维体系,对于一维体系的研究较少.主要原因是除了碳纳米管、纳米线等少数准一维结构外[20−22],实际缺乏真正的一维材料体系,并且实验又难以合成真正的一维材料.由于一维Rashba 体系在固体中观测Majorana 费米子实验中发挥重要作用,因此,研究一维结构中的Rashba 效应具有重要意义.最近人们在实验中相继获得了Te 原子链的块体及被包覆的一维原子链[23−25].理论计算预言,Se 和Te 的块体相在费米能级附近有多个Weyl 节点[26].第一性原理计算发现Te 原子链具有较大的Rashba 劈裂[27].对于一维Se 原子链结构,早期有第一性原理计算研究其能带和GW 准粒子谱[28],对于其稳定性、SOC 效应及其对应力的响应有待人们深入研究.
本文采用第一性原理计算研究了一维螺旋结构Se 原子链的稳定性、电子结构及应力调控规律.结果发现,这种一维螺旋结构具有动力学和热力学稳定性.能带结构计算表明,它是带隙约为2.0 eV的半导体,价带和导带都发生了类似Rashba 效应的自旋劈裂.此外,在5%的应力作用下,其带隙和Rashba 自旋劈裂能产生超过20%的变化,而其价带是一条平带,通过空穴掺杂可以得到铁磁性、半金属等丰富的电子性质.
2 计算方法
本文所涉及的第一性原理电子结构计算采用维也纳从头计算模拟软件包(Viennaab initiosimulation package,VASP)得到[29].其中,电子与原子核之间的赝势是采用投影缀加平面波(projector augmented wave,PAW)方法产生[30,31];电子与电子之间的交换关联泛函采用基于广义梯度近似(generalized gradient approximation,GGA)的Perdew-Burke-Ernzerhof (PBE)泛函[32].平面波截断能为300 eV.对于其一维布里渊区,采用1 ×1 × 12Γ 中心的k网格进行采样.在结构弛豫过程中,能量为1 × 10–6eV,每个原子上力的收敛标准为1 × 10–3eV/Å.声子谱的计算采用基于小位移方法的Phonopy 完成[33].
3 结果与讨论
3.1 一维螺旋Se 原子链的结构与稳定性
在Se 原子形成的晶体中,Se 原子以共价键的形式结合.根据其电子组态的特点可知,每个Se原子有两个近邻原子,因此倾向形成一维螺旋链状结构.在块体中,链与链之间以范德瓦耳斯形式的相互作用结合[25].因此,预期可以利用机械剥离的方式从其三维晶体中得到一维原子链.如图1(a)所示,这种一维结构的原胞中有3 个Se 原子,从正面看,3 个原子以螺旋形式形成周期性结构.图1(b)为一维螺旋Se 原子链结构及直线型结构的总能随晶格常数a的变化图.为了便于比较总能,直线型结构用的是3 倍超胞(即单胞中有3 个Se 原子).可以看出,一维螺旋Se 原子链结构的晶格常数大约为4.96 Å,与Andharia 等[28]计算一致;且螺旋型结构的能量远远低于直线型结构.因此,螺旋型结构的稳定性要高得多.图1(c)给出了螺旋型结构的声子谱.在采用最小位移方法计算某一原子偏离平衡位置移动而导致其他原子上产生力的过程中,沿晶格周期方向取6 倍超胞,以保证力的收敛性.从图1(c)可以看出,声子谱没有虚频,说明其在动力学上是稳定的.图1(d)给出了300 K 时的ab initio分子动力学方法模拟结果,计算中也是采用6 倍超胞.可以看出,整个模拟过程中结构保持得比较好,证明了其热力学稳定性.因此,Se 的一维螺旋结构在动力学和热力学上都是稳定的.
3.2 能带结构与应力调控
图2(a)给出的是没有考虑SOC 计算的能带,可以看出,这种结构的Se 原子链是能隙为2.0 eV的半导体,与文献[28]的计算结果一致;其导带底(conduction band minimum,CBM)在X点,而价带顶(valence band maximum,VBM)在Γ 点.因此,一维螺旋Se 原子链是间接带隙半导体.考虑SOC 以后,能带发生了劈裂.由于靠近X点附近的能带发生的劈裂较大,所以价带顶不再位于Γ 点,而是移动到Γ-X之间的位置.注意到导带和价带在X点附近发生了类似Rashba 的自旋劈裂(见图2(c)插图),其中导带的Rashba 能量偏移ER大约为4 meV,而Rashba 动量偏移kR约为0.2 Å–1.由此可以估算Rashba 参量αR=2ER/kR大约为0.4 eV·Å,比Au(111)表面的0.33 eV·Å稍大[5].
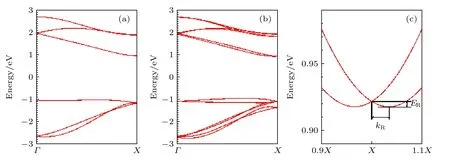
图2 一维螺旋结构Se 原子链的能带结构 (a) 不考虑SOC;(b) 考虑SOC;(c) 考虑SOC 时X 点附近的导带Fig.2.Band structures of the one-dimensional helical Se atomic chain:(a) Without SOC;(b) with SOC;(c) the conduction bands near X from SOC calculations.
螺旋型原子链结构的特点是其易于应力调控.当施加较大的拉伸或压缩应变时,不仅能使结构形状保持得很好,还能有效调控其电子结构.图3(a)给出了能隙随应变的变化,可以看出压缩应变使其能隙增加,而拉伸应变使能隙迅速减小.施加5%的拉伸应变可以使其能隙减小到大约1.5 eV,变化幅度超过20%.这种能隙的变化趋势可以这样理解:由于Se 原子链的能隙是近邻Se 原子间的轨道杂化引起,因此,杂化越强能隙越大.拉伸应变使原子间距增大,故原子间轨道杂化减小,从而带隙也随之减小.相反,压缩应变使原子间轨道杂化增强,因此,能隙变大.图3(b)给出了Rashba能量偏移ER和动量偏移kR随应变力ε 的变化.ε=其中a0为平衡体积时的晶格常数(4.96 Å),a为施加拉伸或压缩后的晶格常数.可以看出,拉伸应变使两者缓慢减小,而压缩应变使其迅速增加.当应变达到–5%时,ER和kR分别增加到平衡体积时的2.3 倍和2.9 倍.总的趋势是压缩应变使αR减小,而拉伸应变使αR增大.

图3 一维螺旋结构Se 原子链的应力调控 (a) 带隙随应变的变化;(b) Rashba 能量偏移(上)和动量偏移(下)Fig.3.Strain tuning of the one-dimensional helical Se atomic chain:(a) Band gap vs.strain;(b) Rashba energy(up) and momentum (bottom) offsets.
3.3 平带性质
图2(a)的能带结构表明,一维螺旋型Se 原子链的价带是一条平带,其带宽约为100 meV.如此平的能带在掺入空穴使费米能级位于价带中时,可能导致新奇的物理现象或电子性质.根据计算结果发现,掺入少量空穴时体系仍然保持无磁状态.当每个原胞掺入0.3 个空穴时(Nh表示每个原胞中空穴的数目,即空穴浓度),体系开始出现铁磁性,但每个原子仅具有很微弱的磁性.进一步增加空穴掺杂浓度,Se 原子上的磁矩逐渐增大.当空穴浓度为1.6 时,磁矩达到最大值0.31µB.随后磁矩开始随空穴浓度的增加而减小.图4(a)给出了平均每个Se 原子上的磁矩随空穴掺杂的变化.由于这种磁性类似巡游电子的磁性,而不是局域电子产生的磁性,因此每个原子上的磁矩不是整数.能带计算表明,当出现铁磁性时,体系由半导体转变为半金属.图4(b)给出了Nh=1.0 时的能带结构,此时,刚好将自旋少子的价带占满.当空穴浓度超过1.6,磁性开始减弱的同时,体系由半金属转变为铁磁金属.图4(c)给出了Nh=2.0 时的能带结构,可以看出,在费米能级处出现了两种不同的自旋态.因此,Se 原子上的磁矩减小,同时体系由半金属转变为铁磁金属态.考虑SOC 效应时,其计算具有同样的趋势.

图4 空穴掺杂浓度 Nh 对一维螺旋Se 原子链结构的影响(a) 平均每个Se 原子的磁矩随 Nh 的变化(FM 代表铁磁序);(b) Nh=1.0 和(c) Nh=2.0 的能带结构 (虚线代表费米能级)Fig.4.Influences of the hole doping concentration Nh on the structure of one-dimensional helical Se atomic chain:(a) The average magnetic momentum per Se atomic vs.Nh(FM denotes the ferromagnetic ordering);band structures with (b) Nh=1.0 and (c) Nh=2.0 (The dotted line represents the Fermi level).
文献[27]的结果表明,Te 原子链的价带也是一条平带.因此,可以预期空穴掺杂可能也会诱导铁磁性和半金属态的出现.为此,我们进一步针对Te 原子链做了计算,结果确实如预期.不同的是,Te 原子链在Nh=0.4 时出现磁性.
4 结论
本文采用第一性原理计算研究了一维螺旋型Se 原子链结构的电子结构.结果发现,螺旋型结构比直线型结构能量要低得多,并且结合声子谱和ab initio分子动力学模拟研究了其动力学和热力学稳定性,研究了其能带结构及自旋轨道耦合效应.结果表明,这种螺旋型原子链是带隙约为2.0 eV的半导体,并且在X点附近展现出类似Rashba 的自旋劈裂.之后,研究了应变对其能隙和自旋劈裂的影响.结果表明,压缩应变使其能隙增大,而拉伸应变使其能隙迅速减小到1.5 eV.此外,这种结构的Se 和Te 原子链的价带都是一条平带,空穴掺杂会诱导磁性的出现.通过控制空穴的浓度,体系可以展现出半导体-半金属-铁磁金属等多种性质,为人们调控这类一维螺旋原子链的电子性质提供理论指导.

