过渡金属二硫化物/三卤化铬范德瓦耳斯异质结的反折叠能带*

邓霖湄 司君山 吴绪才 张卫兵

(长沙理工大学物理与电子科学学院,柔性电子材料基因工程湖南省重点实验室,长沙 410114)

过渡金属二硫化物MX2/三卤化铬CrX3 组成的范德瓦耳斯异质结能有效操控MX2 的谷极化,在能谷电子学中有广泛的应用前景.本文结合第一性原理和k 投影能带反折叠方法比较研究了MoSe2/CrI3,MoSe2/CrBr3 和WS2/CrBr3 三种磁性范德瓦耳斯异质结的堆垛和电子结构,探索了体系谷极化产生的物理机理.计算了异质结不同堆垛的势能面,确定了稳定的堆垛构型,阐明了时间/空间反演对称破缺对体系电子结构的影响.由于轨道杂化,磁性异质结的导带情况复杂,且MoSe2/CrI3 体系价带顶发生明显变化,不能与单层MX2直接对比.而借助于反折叠能带,计算清晰揭示了CrX3 对MX2 电子结构的影响,定量地获得了MX2 的能谷劈裂,并发现层间距和应变可以有效调控能谷劈裂.当层间距减小到2.6 Å 时,AB 堆垛的MoSe2/CrI3 谷劈裂值可达到10.713 meV,是平衡结构的8.8 倍,相当于施加约53 T 的外磁场.通过k 投影能带反折叠方法克服了异质结超胞电子结构不易分析的局限性,对其他磁性范德瓦耳斯体系的研究具有重要的借鉴意义.

1 引言

近年来,以能谷自由度为信息载体的能谷电子学[1–5]受到了人们的极大关注.相似于电荷和自旋,能谷自由度作为一种新的二进制信息编码,可用于信息存储和处理.由于具有空间反演对称破缺、直接带隙和强的自旋轨道耦合(SOC)效应,单层过渡金属二硫化物MX2(M=Mo,W,X=S,Se,Te)被认为是谷电子学的理想候选材料[1–3,6–12].MX2在二维布里渊区形成一对能量简并但不等价的K+/K–能谷,如何打破能谷简并,实现能谷的操控是当前能谷电子学面临的首要问题.

基于能谷选择的圆偏振二色性,研究人员提出通过偏振光泵浦实现谷极化和谷霍尔效应[13,14],并在实验中得到了广泛应用.然而,光泵浦作为一种动力学过程很难稳健地操控,不适合能谷电子学应用.磁性原子掺杂[15]可以打破时间反演对称性,但倾向于形成团簇导致杂质散射增强,进而影响器件性能.早期的实验还观察到外磁场引起的能谷劈裂,但效率极低,仅为0.1—0.2 meV/T[16–20].随后的实验和理论研究还表明,大的能谷劈裂可以通过邻近效应诱导的塞曼效应来得到[21,22].计算预言EuO 衬底上的单层MoTe2的能谷劈裂可以达到300 meV[21].传统磁性异质结基于三维铁磁体,表面存在缺陷和晶界等不可控因素.

单层CrI3[23,24]和双层Cr2Ge2Te6[25]中本征铁磁的实验发现为磁性范德瓦耳斯异质结的发展迎来了新的契机.作为最早实验制备成功的单层铁磁材料,二维CrX3也被广泛应用于构建磁性范德瓦耳斯异质结[26,27].如Zhong 等[27]通过竖直堆积磁性CrI3薄层和单层WSe2,在WSe2中诱发高达13 T 的交换场.二维磁性材料缺乏悬挂键,层间通过范德瓦耳斯力结合,不存在传统异质结中的晶格匹配问题,可以避免化学修改及三维磁体中界面缺陷等不可控因素,产生均匀磁交换场,诱发能谷极化.理论上,人们也研究了多种CrX3/MX2磁性范德瓦耳斯异质结[28–30],证实了磁性单层可以诱发MX2的能谷极化.但在实际模拟中往往采用MX2超胞构建磁性异质结,导致能带折叠,磁性异质结电子结构变得复杂,不易与MX2原胞进行直接对比.另外,形成磁性异质结后,价带顶或导带底可能不再位于K+与K–能谷,能带结构混乱,很难清楚地分析MX2的电子结构细节,如能谷极化.

针对上述问题,本文结合第一性原理和k投影能带反折叠方法研究了MX2/CrX3磁性范德瓦耳斯异质结的堆垛能和电子结构,准确揭示了CrX3对MX2能带的影响.并细致分析异质结的势能面,获得了稳定的堆垛构型,揭示了自旋劈裂和能谷劈裂情况.此外,还比较研究了MoSe2/CrI3,MoSe2/CrBr3与WS2/CrBr3三种异质结,分析了异质结电子结构变化的微观机理.最后,还通过改变层间距与应力对过渡金属二硫化物单层的谷极化进行了调控.借助反折叠能带,清楚地揭示了MX2能谷极化产生的物理机理,对其他磁性范德瓦耳斯异质结的研究具有重要的指导意义.

2 计算方法

本文所有密度泛函理论计算均通过VASP 代码[31,32]进行,采用PAW 方法[33,34]和Perdew-Burke-Ernzerhof (PBE)[35]形式的交换相关泛函.计算采用500 eV 的平面波截断能和9×9×1的k点网格.为避免相邻超胞之间的相互作用,采用大于15 Å的真空层.结构优化收敛标准为每个原子的力小于0.01 eV/Å.为了考虑Cr-3d 电子的电子关联效应,计算采用了GGA+U方法[36],其中库仑相互作用U和交换相互作用J分别设置为3.0 和1.0 eV.同时还采用了Grimme DFT-D2[37]方法考虑了层间范德瓦耳斯相互作用.

为了准确描述磁性单层CrX3对MX2电子结构的影响,计算还采用k投影能带反折叠代码KPROJ[38–40]获得了MoSe2原胞的反折叠能带.KPROJ 代码拥有独特的波函数层投影功能,通过傅里叶变换和傅里叶逆变换相结合,可以高效地研究特定空间范围内的电子性质,获得异质结中不同组分贡献,十分适合范德瓦耳斯异质结的能带反折叠研究.

3 结果与讨论

3.1 堆垛结构

为比较研究CrX3对MX2电子结构的影响,本文构建了MoSe2/CrI3,MoSe2/CrBr3和WS2/CrBr3三种磁性范德瓦耳斯异质结.MoSe2,WS2,CrBr3和CrI3的晶格常数分别为3.33,3.200,6.45和6.90 Å.为减小晶格失配率,文中双层MX2/CrX3磁性异质结由2×2的MoSe2和1×1的CrI3组成(如图1 所示),异质结的晶格参数与2×2的MX2晶格常数一致.如表1 所列,MoSe2/CrI3,MoSe2/CrBr3和WS2/CrBr3三种磁性范德瓦耳斯异质结的晶格失配率分别为4.9%,3.1%和0.7%,均小于5%,表明三种磁性异质结在实验上是可行的.对应的布里渊区如图1(c)所示,异质结布里渊区仅为MX2原胞布里渊区的一半.

表1 三种异质结不同堆垛的自旋和能谷劈裂(单位:meV)Table 1.The spin splitting and valley splitting in unit of meV of three vdW heterostructure with different stacking order.

根据两种组成单层的相对位移,异质结可以形成多种不同的堆垛.保持MX2层不变,通过把CrX3平移n/6a+m/6b (a 和b 为异质结平面晶格矢量,n,m取0—6),构建了36 种不同的堆垛结构,同时固定平面坐标,优化z轴坐标计算其能量,最后通过插值获得了异质结的堆垛势能面.如图2(a)—(c)所示,三种异质结的势能面结构非常相似,异质结能量最低的结构为AB,同时还存在一种亚稳堆垛结构AB′.值得注意的是,AB和AB′堆垛均处于势能面的能量极小值点,对应一阶导数为0,二阶导数大于0,表明这两种结构均为稳定(亚稳)结构,在一定条件下可以稳定存在.如图1(b)所示,AB结构中一个Cr 原子在Se 原子的正上方,而另一个Cr 原子位于正六边形中心.而在AB′中,一个Cr 原子位于Se 原子的正上方,另一个位于Mo 原子的正上方.

图1 MoSe2/CrI3 异质结的结构和布里渊区 (a),(b)对应于AB 和AB′ 堆垛的MoSe2/CrI3 结构;(c)大六边形和小六边形分别对应MoSe2 原胞布里渊区和异质结布里渊区Fig.1.Structure and Brillouin zone of MoSe2/CrI3 heterostructure:(a),(b) MoSe2/CrI3 heterostructure with the AB and AB′ stacking,respectively;(c) the large and small hexagon correspond to the MoSe2 protocell Brillouin region and the heterojunction Brillouin region,respectively.

图2 (a) MoSe2/CrI3, (b) MoSe2/CrBr3 和(c) WS2/CrBr3 体系的堆垛势能面图Fig.2.Stacking potential energy surfaces of (a) MoSe2/CrI3,(b) MoSe2/CrBr3 and (c) WS2/CrBr3.

为分析能量与堆垛的关系,计算了MoSe2/CrI3异质结的自旋电荷密度.如图3(a)和图3(b)所示,可以看出,在CrX3的下方积聚了自旋向上的电荷(黄色部分A).由于CrX3具有磁性,使得不具有自旋极化的MX2在形成异质结时X原子产生了自旋极化,在其上方积聚自旋向下的电荷(蓝色部分B).定义上层自旋向上的电荷中心(黄色部分A)到最近邻下层自旋向下的电荷中心(蓝色部分B)的距离为d.图3(c)给出1/d随堆垛的变化情况,可以看出,其变化趋势与能量随堆垛变化的趋势非常相似,表明堆垛能主要由层间电荷间的库仑相互作用支配.由于层间平移改变了层间电荷中心的距离,从而引起了库仑势的变化,最终导致了能量随堆垛的变化.相似的机理也在双层CrBr3中被发现[41].

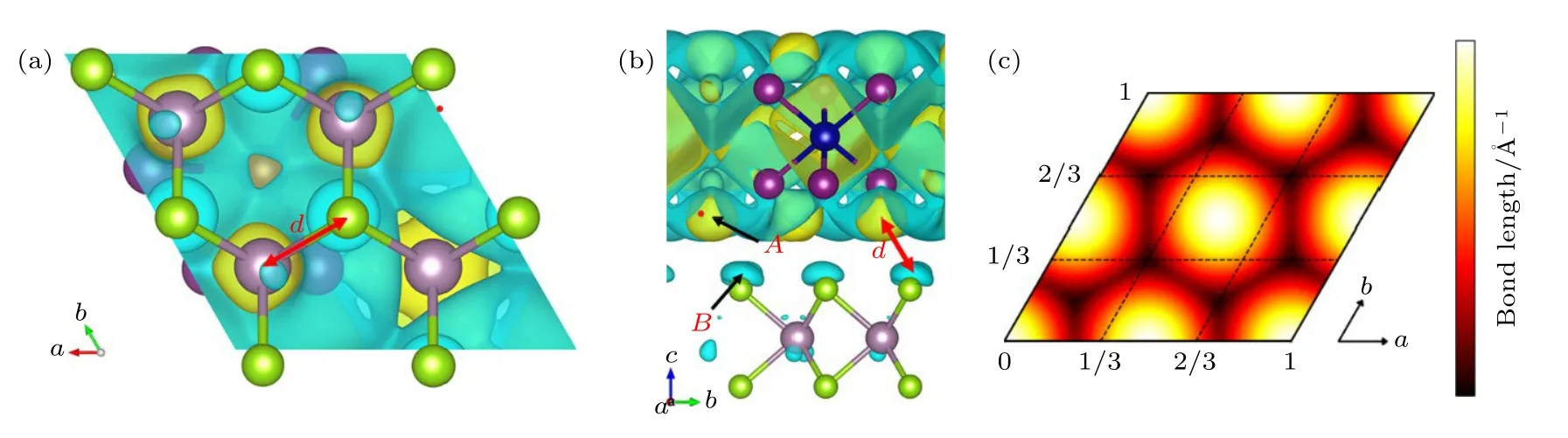
图3 MoSe2/CrI3 的自旋电荷密度分布 ((a)和(b))以及层间1/d随堆垛的变化图(c)Fig.3.The spin density distribution ((a) and (b)) of MoSe2/CrI3,and the variation of 1/d with different stacking (c).

3.2 电子结构

磁性异质结中的铁磁CrX3单层能打破时间反演对称,诱发新奇的能谷物理.由于不同堆垛的磁性异质结具有相似的电子结构和机理,下面以AB堆垛的MoSe2/CrI3为例讨论CrX3对MX2的电子结构影响.如图4(a)所示,不考虑自旋极化与自旋轨道耦合时,单层MoSe2具有直接带隙.由于单层MoSe2是非磁,电子结构受时间反演对称保护.所有能带具有二重自旋简并,导带底与价带顶位于K+/K-能谷,且K+和K-谷的能量相等.考虑自旋极化但不考虑自旋轨道耦合时,由于体系仍是非磁状态,因此K+/K-谷的能带依然简并(图4(b)).考虑自旋轨道耦合(SOC)时,K+谷和K-谷的能带是自旋相反、能量简并,产生自旋劈裂,如图4(c)所示.

图4 MoSe2,CrI3 和AB 堆垛 MoSe2/CrI3 的能带图 (a)—(c)分别对应单层MoSe2 不考虑自旋极化且不考虑自旋轨道耦合时、考虑自旋极化以及考虑自旋极化和自旋轨道耦合时的能带;(d)—(f)对应CrI3 的情况;(g)—(i)对应 AB 堆垛 MoSe2/CrI3Fig.4.Band structure of MoSe2,CrI3 and AB-stacking MoSe2/CrI3 vdW heterostructure:(a)–(c) The energy band obtained without spin polarization and spin orbital coupling,with spin polarization and with spin polarization and spin orbital coupling;(d)–(f) the case of CrI3;(g)–(i) the corresponding energy band of AB-stacking MoSe2/CrI3.

CrI3中的Cr3+具有3d3电子构型,Cr 原子处于有畸变的八面体场中,d 电子将近似分裂成三重简并的t2g和双重简并的eg轨道.不考虑自旋极化与自旋轨道耦合时,能带具有自旋简并,3 个电子将占据三个二重的t2g轨道,形成金属态(图4(d)).考虑自旋极化但不考虑自旋轨道耦合时,体系出现交换劈裂,根据洪特定则和泡利不相容原理,电子将趋向于高自旋排列,三个d 电子将占据三个自旋向上的t2g轨道,形成半导体,自旋磁矩为 3.0µB/Cr(图4(e)).而进一步考虑自旋轨道耦合(SOC)计算时,Γ点能量提高,CrI3仍保持为半导体(图4(f)).

在AB堆垛MoSe2/CrI3异质结中,不考虑自旋极化与自旋轨道耦合时,计算结果显示费米能级附近电子态由CrI3支配,价带顶为K+/K–谷,能带简并且为金属(图4(g));考虑自旋极化但不含SOC 时,计算结果显示能带依然简并,价带顶仍为K+/K–,且主要由MoSe2贡献,异质结表现为半导体(图4(h));进一步考虑自旋轨道耦合时,由于铁磁衬底打破了时间反演对称性,K+K–谷能量简并被打破,产生自旋劈裂和谷劈裂,同时价带顶由K+/K–变为Γ点(图4(i)).

3.3 反折叠能带

如前所述,单层MoSe2的价带顶在K+/K–谷,形成异质结后,VBM 变成了Γ点.为进一步分析VBM 变化的微观机理,研究了MoSe2/CrI3轨道投影能带图.如图5(a)—(d),异质结导带底(CBM)主要由CrI3贡献,MoSe2的导带淹没在CrI3的导带中.而价带顶(VBM)由MoSe2和CrI3共同贡献,其中Γ点附近的价带主要由I-p 轨道贡献,在K+和K–谷主要由Mo-p 贡献.如图5(e)—(h),MoSe2/CrBr3的导带底与MoSe2/CrI3一致,主要由CrBr3所贡献;而价带无论在Γ谷还是K+K–谷都主要由Mo-d,Se-p 贡献,基本没有磁性单层的贡献,因此体系价带顶仍保持在K+和K–点.WS2/CrBr3的结果与MoSe2/CrBr3的结果十分类似(图5(i)—(l)).

图5 磁性异质结轨道分辨的能带图 (a)—(d)分别是MoSe2/CrI3 中Mo-d,Se-p,Cr-d,I-p 的轨道投影能带图;(e)—(h)分别是MoSe2/CrBr3 中Mo-d,Se-p,Cr-d,Br-p 的轨道投影能带图;(i)—(l)对应于WS2/CrBr3 体系Fig.5.Orbital resolved energy band of magnetic heterostructure:(a)–(d) The Mo-d,Se-p,Cr-d,I-p resolved energy band of MoSe2/CrI3;(e)–(h) the correspongding energy band of MoSe2/CrBr3;(i)–(l) the correspongding energy band of WS2/CrBr3.

如前所述,所有异质结的导带主要由铁磁CrX3单层支配,MX2导带被隐藏.另外,MoSe2/CrI3的价带顶也发生了移动.因此很难直接将异质结的能带跟MX2进行对比.为了更加清晰地揭示铁磁半导体对MX2的谷劈裂影响,用k投影能带方法把异质结中超胞波函数反折叠到MoSe2原胞布里渊区.图6 给出了AB堆垛中MoSe2/CrI3中MoSe2的反折叠能带,可以发现异质结中不同组成单层的贡献被完全区分,从而可以跟单层MoSe2的能带直接对比,得到价带和导带的改变情况.从图6(b)和图6(c),可以清晰地看到,由于铁磁CrX3单层打破了MX2的时间反演对称性导致其产生了谷劈裂,K+/K–谷的能带简并被打破,价带和导带的谷劈裂约为1.215 和1.756 meV,自旋劈裂为185—187 meV 和 19—22 meV.更有意思的是,通过与MoSe2单层能带结构的对比,还可以发现异质结Γ点附近由于与CrX3杂化出现新的能带.而AB′堆垛(图6(d))反折叠能带表现出相似的特征,价带和导带谷劈裂值分别为 0.596 和0.940 meV.表1 给出了三种异质结不同堆垛的自旋和能谷劈裂.Zollner 等[42]研究MoSe2/CrI3谷劈裂的扭角、层数和电场依赖性,得到单层无扭角时,MoSe2能谷劈裂为1.13 meV,与本文结果极好地符合.Zhang 等[29]对过渡金属二硫化物/三卤化铬做了比较系统的研究,发现MoSe2/CrI3为3.5 meV.

图6 (a)自旋劈裂和谷劈裂的定义;(b),(c) AB 堆垛的MoSe2/CrI3 中MoSe2 在1×1的布里渊区反折叠能带与单独存在的MoSe2 比较图,其中子图为K+/K–附近的价带和导带情况;(d)—(f)AB′堆 垛 MoSe2/CrI3,AB 堆 垛 MoSe2/CrBr3 和WS2/CrBr3 的反折叠能带图Fig.6.(a) The definition of spin splitting and valley splitting;(b),(c) the comparison between the unfolding band of MoSe2 in ABstacking MoSe2/CrI3 heterostructure and free-standing MoSe2,the VBM (b) and CBM (c);(d)–(f) the unfolding energy band of AB′ stacking MoSe2/CrI3,AB stacking MoSe2/CrBr3 and WS2/CrBr3,respectively.

与MoSe2/CrI3的反折叠能带相比,如图6(e)所示,MoSe2/CrBr3体系价带顶和导带底附近情况基本类似,但可以明显发现Γ点附近没有出现新的能带.AB和AB′堆垛的价带K+自旋劈裂约为184 和185 meV,而对应的价带顶能谷劈裂变为1.852 和2.028 meV.Zhang 等[29]计算的 MoSe2/CrBr3的谷极化为5.6 meV,比MoSe2/CrI3和WS2/CrBr2体系都大,变化趋势跟本文的预测一致.Ciorciaro 等[43]使用共振光学反射光谱在MoSe2/CrBr3异质结中观察到了谷劈裂效应,其谷劈裂为2.90 meV,与本文的计算结果非常接近,表明了本文结果的合理性和准确性.

而对WS2/CrBr3体系,价带自旋劈裂增大为435 meV,对应能谷劈裂变为 0.67 和0.27 meV,比其他体系小.Zhang 等[29]计算的结果为1.4 meV,也比其他两个体系小.另外还跟WSe2/CrI3体系进行了对比.理论计算发现WSe2/CrI3的能谷极化为0.5 meV[44],0.27—0.43 meV[45],0.3—1.04 meV[30]和1.61 meV[42],与本文的计算类似.另外,分析了导带底能谷劈裂的情况,发现三种异质结导带底也存在明显的能谷劈裂,略大于价带顶.值得注意的是,在实验上制备的WSe2/CrI3范德瓦耳斯异质结[27],具有转角莫尔条纹结构,谷劈裂约为3.5 meV,大于本文和文献中的计算结果.近来研究也发现,转角能极大地增加能谷劈裂[42,45].因此实验和理论的差距可能来源于实验上观察到的是具有转角的异质结,而计算采用了晶格匹配的结构.

3.4 层间距和应变调控

为提高MX2的谷劈裂,尝试通过层间距与应力调控体系的能谷极化.图7(a)和图7(b)给出了AB堆垛MoSe2/CrI3的谷劈裂和能量随层间距的变化关系图.层间距为层间最近邻的Se 原子和I 原子的垂直距离.本文计算层间距从2.6 到7.0 Å异质结的能谷劈裂,发现谷劈裂随着层间距的减小而增大,当层间距为2.6 Å 时,谷劈裂值可达到10.713 meV,相当于施加 53 T 的外磁场,是平衡结构的8.8 倍.另外,当层间距小于2.4 Å时,AB堆垛异质结由半导体变为金属.对AB′堆垛,当层间距小于 2.4 Å时,异质结也会发生半导体-金属转变.当层间距约为2.6 Å时,谷劈裂值可达到8.924 meV,相当于施加 45 T 的外磁场.随着层间距的增加,铁磁单层对MoSe2影响减弱,谷劈裂基本保持不变.

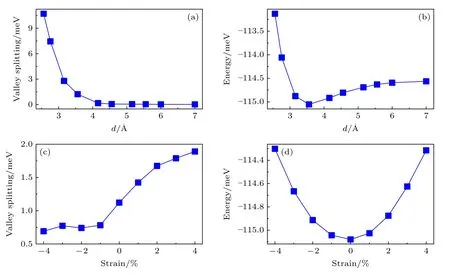
图7 AB 堆垛 MoSe2/CrI3 能谷劈裂和能量随层间距和应力的变化 (a),(b)能谷劈裂和能量随层间距的变化关系;(c),(d) AB堆垛MoSe2/CrI3 的能谷劈裂和能量随应变的变化关系Fig.7.The change of valley splitting and energy with interlayer distance and strain of MoSe2/CrI3:(a),(b) The change of valley splitting and energy with interlayer distance;(c),(d) change with strain.

另外还研究了应变对异质结谷劈裂的调控(图7(c)和图7(d)),应变定义为其中a为面内晶格常数,a0为面内平衡晶格常数.计算了–4%—4%应变条件下异质结的能谷劈裂.结果发现压应变下谷劈裂变小,但随着拉应变而单调增加.4%的应变下,谷劈裂增大到1.8 meV.相比于层间距,谷极化随着应变变化不明显.

4 结论

结合第一性原理和k投影能带反折叠方法,本文定量研究了三种MX2/CrX3铁磁异质结构堆垛和电子结构.堆垛势能面计算发现异质结存在AB和AB′两种稳定的堆垛构型.还分析了MX2,CrX3及磁性异质结的电子结构,阐明了时间/空间反演对称破缺对体系电子结构的影响.为了更清晰地研究铁磁半导体上MX2的能谷劈裂,我们获得了磁性异质结中MX2反折叠能带,定量分析了不同体系的能谷劈裂,并与已有的实验和理论进行了详细对比.另外还发现,减小层间距可以把能谷劈裂提高近10 倍,表明层间距是调控异质结能谷劈裂的有效手段.