氮气分子和b1Πu 电子态的不透明度*

陈晨 赵国鹏 祁月盈 吴勇 王建国3)

1) (复旦大学,现代物理研究所,上海 200433)

2) (嘉兴学院数据科学学院,嘉兴 314001)

3) (北京应用物理与计算数学研究所,计算物理重点实验室,北京 100088)

4) (北京大学工学院,应用物理与技术研究中心,北京 100871)

采用考虑Davidson 修正的多参考组态相互作用(MRCI+Q)方法,计算了氮气分子和b1Пu 电子态的势能曲线、偶极跃迁矩阵元、光谱常数和振动能级,计算结果与其他实验和理论数据符合较好.基于分子结构数据,研究了氮气分子在100 atm (1 atm=1.01×105 Pa)压强下,295—20000 K 温度范围内的不透明度.结果表明,在波长分布范围内,不透明度随着温度的升高而变大;当温度小于5000 K 时,不透明度主要分布在紫外区域,当温度大于10000 K 时,激发态的贡献使得不透明度在红外区域也开始有明显的布居.本文探明了温度效应对氮气分子不透明度的影响,可以为天体物理和核武器领域提供理论和数据支持.

1 引言

辐射不透明度在天体物理、等离子体物理、原子核物理等领域都有重要应用[1-5],对大气分子不透明度的研究有助于了解大气的辐射输运过程[6].氮气分子广泛存在于地球、土卫六和海卫一等天体中[7],在天体物理的研究中有重要的作用.目前,人们对富含氮气分子的大气发射光谱进行了广泛观测[8-10],为了分析观测到的大气光谱数据并建立数学模型,必须探究清楚氮气分子的光谱性质[11-13].例如,高层大气辉光观测中用到的掩日法和辐射转移模型都需要氮气分子的光谱数据[14].并且由于氮气分子广泛存在于地球大气中,通过计算其不透明度有助于研究空气对核武器爆炸后产生的辐射的吸收能力,从而判断核武器的破坏能力.数据库HITRAN(high-resolution transmission molecular absorption database)[15-19]广泛应用于分子不透明度的研究,它不仅提供可靠的光谱参数,而且通过光谱参数可模拟不同温度范围的吸收和发射光谱.

早在20 世纪,人们已经对氮气分子的光谱进行了大量实验观测.1977 年,Lofthus 和Krupenie[20]对观测到的光谱数据进行了综述.1992 年,Stark 等[21]测量了在295 K 的温度条件下氮气分子的吸收截面.2005 年,该实验组在相同温度条件下测量了跃迁过程的吸收截面[14].同年,Haverd 等[22]在室温条件下对跃迁过程的极紫外吸收谱进行了实验测量和理论分析.2006 年,Robert 等[23]测量了295,535 和600 K的温度条件下的振转分辨的振子强度.2015 年,Niu等[24]观测了温度达到900 K 时氮气分子跃迁过程的吸收谱的谱线线移和展宽.2019 年,Heays 等[25]观测了14N15N 的吸收谱.

对于氮气分子,人们还开展了大量的理论研究工作.Spelsberg 和Meyer[26]在2001 年采用耦合簇方法和MRCI 方法研究了电子态的势能曲线、光谱常数和偶极跃迁矩阵元.San-Fabián和Pastor-Abia[27]在2003 年采用完全活性空间自洽场方法(CASSCF)并结合密度泛函理论(DFT)给出了9 个低激发态的势能曲线.Hochlaf 等[28]在2010 年采用MRCI 方法计算了解离极限分别为N(4Su)+N(4Su),(4Su)+N(2Du),(4Su)+N(2Pu)和N(2Du)+N(2Du)的电子态的势能曲线.2012 年Shi等[29]通过MRCI 方法给出了N2体系三重态的光谱常数.Xin 和Ding[30]在2014 年采用CASSCF方法计算了基态和低激发态的势能曲线和偶极跃迁矩阵元.Lavín 和Velasco[31,32]在2010 和2011年研究了室温条件下和跃迁的吸收谱,并且从2016 年到2021 年研究了氮气分子不同跃迁过程振转分辨的跃迁能和振子强度[33-36].Qin 等[37]和Liang 等[38]分别在2019 年和2021 年计算了氮气分子的辐射跃迁几率.

如上所述,虽然已经有大量的实验工作观测了不同温度条件下的氮气分子光谱,但是针对氮气分子的理论工作主要关注的是光谱常数和分子结构的计算.而氮气分子光谱在天体物理和核武器中都有非常重要的应用,本工作选取典型的冷星大气的压强参考值100 atm (1 atm=1.01×105Pa)[39],系统地研究不同温度条件下氮气分子的不透明度,为天体物理和核武器领域提供理论和数据支持.本文第2 节将给出采用的计算方法,第3 节给出计算结果与理论分析,第4 节给出研究结论.除特别提及,本文均采用原子单位.

2 计算方法

分别利用MOLPRO[40]和LEVEL[41]程序计算氮气分子的电子结构和光谱常数.计算中首先使用Hartree-Fock 方法并采用aug-cc-pCV5Z-DK 基组[42],在核间距0.8—6.0 Å范围内计算了氮气的分子轨道,再利用CASSCF 方法[43]得到参考波函数,最后用包含Davidson 修正[44]的MRCI方法[45,46]计算得到电子结构.由于MOLPRO 程序中使用的是阿贝尔点群,因此氮气分子所属的D∞h点群需要替换为D2h子群,其不可约表示转换关系为:,∏g→ B2g+B3g和∏u→B2u+B3u.在CASSCF的计算过程中选取氮原子2s2p壳层的8 个分子轨道(2 个Ag,1 个B3u,1 个B2u,2 个B1u,1 个B2g和1 个B3g)作为活性空间.

在Born-Oppenheimer 近似条件下,双原子分子的哈密顿量可以写为电子和核的哈密顿量之和,即

体系总波函数Ψ(r,R) 可以表示为电子和核的波函数乘积的形式:

Ψe(r,R)和χ(R) 分别由下面的电子和核的薛定谔方程确定:

其中Ee(R) 是由分子核间距确定的势能,µ是分子的约化质量,J是转动量子数,EvJ是振转能级.

分子不透明度的表达式为

式中E′′是两个态间的能级差,是振转激发能,h是普朗克常数,k是玻尔兹曼常数,c是光速,T是热力学温度.

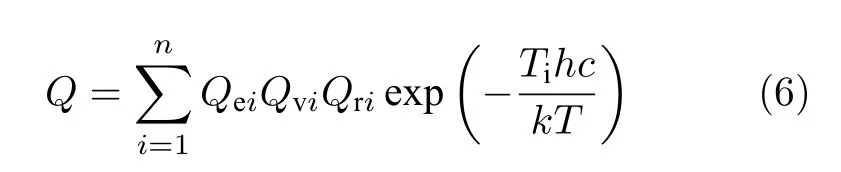
是分子总的配分函数,可以表示为电子、振动和转动配分函数乘积的形式,其中Ti是激发能.

3 计算结果与分析

3.1 势能曲线、光谱常数和振动能级

首先计算势能曲线、光谱常数和振动能级间隔,进而研究氮气分子的不透明度,并将相关数据与可得的其他理论和实验结果进行对比.

基于势能曲线计算氮气分子的光谱常数.表1列出了跃迁能Te、振动常数we和wexe、转动常数Be、平衡核间距Re和解离能De,同时还给出了对应的实验值以及过去的理论结果,其中文献[43,45]的对比数据采用的基组均为cc-pVQZ.与其他理论结果相比,本工作中基态的Be,Re和De与实验结果符合得较好,we和wexe的值2357.1168 cm—1和14.3883 cm—1与实验结果的偏差也仅为0.06%和0.45%.激发态的Te,we,Be,Re和De与实验结果符合得较好,wexe的值11.4479 cm—1与采用MRCI[28]方法计算的结果11.91 cm—1以及实验结果[20]12.1 cm—1基本一致.激发态a1Пg的we,Be,Re和De与实验结果符合得较好,Te和wexe的值69486.425 cm—1和13.6099 cm—1与实验结果的偏差分别为0.77%和2.13%.激发态b1Пu的Te和Re与实验值[51]分别相差0.67%和2.73%,解离能De与实验结果[20]相差3.40%,并且与采用MR-AQCC方法计算的理论结果[43]符合得较好,仅相差0.72%.

表1 氮气分子的光谱常数Table 1.Spectral constants of nitrogen molecular.

表2 氮气分子态的振动能级间隔(Ev—Ev—1)(单位:cm—1)Table 2.Vibr ational level spaceings (Ev—Ev—1) (in cm—1) for state of nitrogen molecular.

表2 氮气分子态的振动能级间隔(Ev—Ev—1)(单位:cm—1)Table 2.Vibr ational level spaceings (Ev—Ev—1) (in cm—1) for state of nitrogen molecular.

表3 氮气分子 a1Πg 和 b1Πu 态的振动能级间隔(Ev — Ev—1)(单位:cm—1)Table 3.Vibrational level spaceings (Ev — Ev—1)(in cm—1) for a1Πg and b1Πu states of nitrogen molecular.

表3 氮气分子 a1Πg 和 b1Πu 态的振动能级间隔(Ev — Ev—1)(单位:cm—1)Table 3.Vibrational level spaceings (Ev — Ev—1)(in cm—1) for a1Πg and b1Πu states of nitrogen molecular.

3.2 跃迁矩阵元和配分函数

为了考虑温度效应对氮气分子不透明度的影响,下面在计算跃迁矩阵元的同时,还给出了配分函数随温度的变化关系.图2 给出了采用MRCI方法给出的核间距0.8—6.0 Å内氮气分子的偶极跃迁矩阵元.图中曲线显示,跃迁矩阵元在核间距大于3 Å时都趋于零,说明氮气分子解离为两个中性的氮原子.氮气分子的配分函数是在上述势能曲线、跃迁矩阵元和振动能级的基础上进行计算的,其随温度的变化关系如图3 所示.配分函数随温度的升高而快速增大,这表明激发态的布居数随着温度的升高而增大.

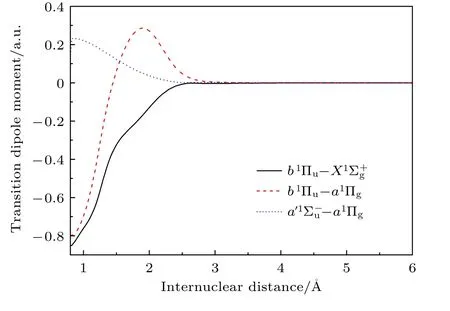
图2 氮气分子的偶极跃迁矩阵元随核间距的变化Fig.2.Transition dipole moments for different states of nitrogen molecular as a function of internuclear distance R.

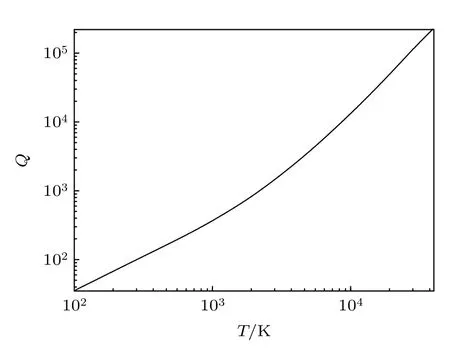
图3 氮气分子的配分函数Fig.3.The partition functions of nitrogen molecular.

3.3 不透明度

基于上述分子结构数据,以及跃迁矩阵元和配分函数,系统研究了100 atm 的压强条件下,不同温度对氮气分子不透明度的影响.在100 atm 的压强条件下,295—2000 K 和2500—20000 K 的温度范围内,氮气分子的不透明度随波长的变化关系如图4 和图5 所示.图4(a)—(d)显示,随着温度的升高,不透明度的最大峰值逐渐减小.例如温度T=295 K 时最大峰值为1.6 × 10—15cm2/molecule,T=2000 K 时最大峰值为2.1 × 10—16cm2/molecule;并且随着温度的升高,不透明度的波长布居范围变大,振动峰值结构变得更加密集.产生这些现象的原因是随着温度升高,分子激发态的布居数将增加,同时更多的氮气分子将解离为氮原子.考虑更大的温度范围,对比图4 和图5 可以发现,温度小于5000 K时,不透明度主要分布在紫外区域,来自的贡献.这是由于这些环境下氮气分子主要布居在基态.随着温度的升高,高激发态布居逐渐增多,特别是当温度高于10000 K 时,不透明度开始在红外区域(来自b1Пu—a1Пg和的贡献)有了明显的分布,如图5(c),(d)所示.另外需要指出的是,温度高于10000 K 时,氮气分子不透明度的谱线强度已经非常小,说明此时大部分氮气分子已经解离为氮原子,在大气分子光谱的研究工作中应该重点考虑氮原子不透明度的贡献.

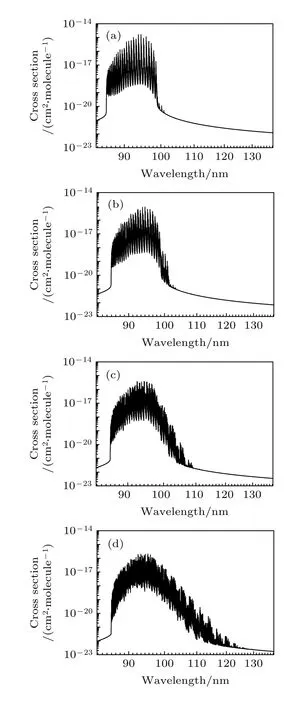
图4 压强为100 atm 时,不同温度下氮气分子的不透明度 (a) 295 K;(b) 500 K;(c) 1000 K;(d) 2000 KFig.4.Opacities of nitrogen molecule at different temperatures under the pressure of 100 atm:(a) 295 K;(b) 500 K;(c) 1000 K;(d) 2000 K.

图5 压强为100 atm 时,不同温度下氮气分子的不透明度 (a) 2500 K;(b) 5000 K;(c) 10000 K;(d) 20000 KFig.5.Opacities of nitrogen molecule at different temperatures under the pressure of 100 atm:(a) 2500 K;(b) 5000 K;(c) 10000 K;(d) 20000 K.

4 结论