地铁车站结构上穿可液化土层地震响应分析

安军海， 闫宏锦， 赵志杰， 蒋录珍

(河北科技大学建筑工程学院， 石家庄 050018)

地震发生时，饱和砂土液化引起的土层大变形是造成地下结构发生震害的主要原因[1-2]。1964年日本新潟地震，引发大面积土体发生液化，致使很多地下管线和铁路隧道结构均出现了不同程度的上浮或破坏[3-4]；1989年美国加州6.9级Loma Prieta地震，致使旧金山港湾地区发生了大面积的砂土液化，例如喷砂冒水、侧向位移、地面沉降及地裂缝等，造成多处地面及地下结构发生严重破坏[5-6]；1995年日本阪神地震，造成了大开地铁车站毁灭性的倒塌，调查发现，由于该车站周围土层比较松散，导致地震时侧向变形很大[7-10]；2011年日本9.0级太平洋近海地震，造成大面积土体液化，很多建筑物发生严重地基沉降，浅埋地下结构甚至出现上浮至地面以上的情况[11-13]。目前，中国正处于城市轨道交通建设的高峰期，越来越多的地铁结构将不可避免地穿越可液化土层，如南京、北京、太原等城市，尤其是太原，穿越可液化地层的轨道交通线路几乎占全部线路的60%以上。因此，开展可液化场地中的地铁地下结构抗震性能研究具有重要工程应用价值。

近年来，相关学者相继开展了一些可液化地层中地下结构的地震响应规律研究。王刚等[14]研究了饱和砂土层中地铁车站结构和周围地层间的动力相互作用，分析了结构埋深对于结构加速度、上浮以及内力的影响。王文章[15]采用有限元软件 DBLEAVES 分析了地震作用下可液化土的动力响应，评估了液化防治措施效果。王建宁等[16-17]、庄海洋等[18]分别对可液化场地中的复杂异形及典型双层三跨地铁车站周围场地进行了模拟，重点分析了结构上浮及周围地基的液化区分布和位移矢量。何剑平等[19]基于FLAC3D软件，验证了液化的隔震作用及碎石排水层法的抗液化效果。刘春晓[20]使用FLAC3D软件，研究了可液化土层位置对地下结构的地震反应。以往研究基本上都把地铁地下结构置于全部的可液化场地中，对上穿一定厚度可液化土层的地铁车站结构地震反应特性还需进一步探讨。此外，《地下结构抗震设计标准》(GB/T 51336—2018)中已明确规定，距结构底部深度10 m内的地层存在饱和砂土时，其抗震设计问题应做专门处理[21]。因此，开展地铁车站结构上穿可液化土层的地震响应规律分析具有重要意义。

基于此，现以北京某典型地铁车站结构上穿厚度为3 m的饱和粉细砂土层的实际工程为研究背景，建立土-地下结构动力相互作用的数值模型，并以相应自由场模拟结果作为对比工况，分析场地液化分布特征、结构应力及上浮特征、周围场地位移沉降及矢量特征等指标，并给出一些有价值的研究结论。

1 数值模型的建立

1.1 结构及场地条件

车站是典型的两层三跨箱型框架式结构，其主体部分横断面尺寸如图1所示。结构覆土厚度为2 m，车站纵梁、中柱及墙板混凝土等级分别为C40、C45、C40，其相应部位的结构参数如表1所示。

图1 地铁车站结构形式及尺寸Fig.1 Structure and size of subway station

表1 结构参数

基于该车站场地的岩土工程勘察报告，选取北京市通州地区含有饱和粉细砂地层的典型场地条件进行适当简化，得到各土层的分布及其物理力学参数如表2所示。

1.2 数值模型及材料本构

基于有限差分软件FLAC3D建立尺寸的长×高=161 m×45 m的数值模型，其顶面取至地表面，下边界取至等效基岩面，模型底部固定；共有3 652个单元和7 820个节点。混凝土结构采用弹性本构模型，场地土层遵循Mohr-Coulomb 强度准则，地铁车站结构下方3 m厚的饱和粉细砂选用PL-Finn模型，结构及土体采用实体单元及局部阻尼，其阻尼系数分别为0.157和0.314。动力计算时，模型底部设置为静态吸收边界，四周施加自由场边界，建立的土-地下结构动力相互作用数值模型及作为对比分析工况的自由场数值模型如图2所示。其中，P1～P4、A1～A11分别为模型土体的孔隙水压力和加速度监测点，Aa～Ae为不同深度处的加速度监测点。

表2 场地土层物理力学参数

图2 数值计算模型Fig.2 Numerical calculation model

1.3 输入地震动

基岩输入地震动选取可最大限度地表征场地土的动力特性的北京人工波，地震动输入时，将其峰值地面加速度(peak ground acceleration，PGA)调整为0.2g(g为重力加速度)，持时为30 s，加速度时程曲线及其相应频谱图如图3所示。

图3 输入地震动的加速度时程及傅氏谱Fig.3 Acceleration time history and Fourier spectrum of input ground motion

2 计算结果分析

2.1 孔隙水压力反应

为分析地震作用下地下结构的存在对饱和砂土层孔隙水压力的影响，图4给出了自由场和非自由场计算工况中距离地铁车站结构左侧墙分别为0.6 m(P1)、5 m(P2)和10 m(P3)的监测点的超孔压比时程曲线。

图4 距离侧墙不同距离超孔压比时程Fig.4 Time history of over pore pressure ratio at different distances from the side wall

由图4可知：无论是自由场还是非自由场计算工况中，在地震动输入的初始阶段(0～7 s)，可液化土层的超孔压比增长缓慢，此时的土体处于弹性状态；随着地震动强度及持时的增加(8～15 s)，超孔压比迅速增加，达到峰值后一段时间内保持平稳。这是由于随着地震动作用的不断累积，使得饱和砂土颗粒之间发生相对滑移导致孔隙体积减小，而这时的饱和砂土地基又处于不排水状态，于是孔压急剧发展；最后，随着地震动强度的逐渐降低(16～30 s)，积聚在饱和砂土地基内的孔压缓慢消散，超孔压比逐渐降低。从输入地震动峰值与孔压发展模式来看，二者达到峰值的时刻接近。

自由场计算工况中，同深度处饱和粉细砂土体(P1、P2、P3)的超孔压比时程曲线几乎完全一致，而非自由场工况中相应位置监测点的超孔压比则明显不同，说明地下结构的存在改变了孔隙水压力的分布规律。从图4(a)中可以看出，距离地铁车站结构越近的土层，其孔压比越大。这主要是因为靠近地下结构的监测点的初始有效应力比较低，而超孔隙水压力需上升至有效应力时才能发生液化。此外，监测点P1接近于左侧墙和底板的连接部位，该部分土体的剪切变形最大，这也在一定程度上促进了孔隙水压力的增加。

11 s时(加速度波峰值时刻)，自由场和非自由场计算工况下场地土的孔隙水压力分布云图如图5所示。

图5 孔隙水压力分布云图Fig.5 Cloud diagram of pore water pressure distribution

由图5可知：非自由场计算工况中地铁车站结构两侧地基的孔压分布区域基本对称分布，靠近侧墙和底板连接范围的土体(区域1)的孔压最大，结构正下方范围土体(区域2)次之，远离结构范围土体(区域3)孔压最小。即地下结构下方存在可液化土体时，从结构远处到近端，孔隙水压力呈先减小后变大的变化趋势。

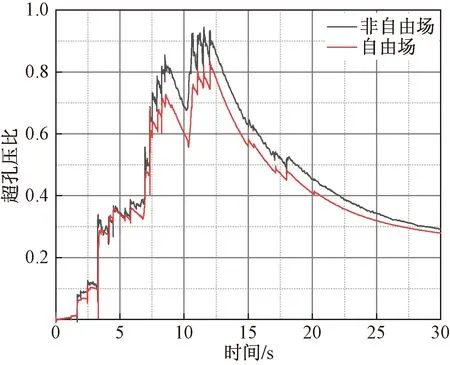
图6 地铁车站结构底板下方超孔压比时程Fig.6 Time history of over-pore pressure ratio under the bottom plate of subway station structure

图6给出了自由场和非自由场计算工况中地铁车站结构正下方监测点P4的超孔压比时程曲线。整体上，不同计算工况下同一监测点的超孔压比增长趋势大体一致，且几乎同时达到峰值，但非自由场计算工况中监测点的超孔压比值大于自由场计算工况中的超孔压比，这是由于同等土体深度处，非自由场中存在地铁车站结构而使得其有效应力比自由场场地中的小，导致土体克服有效应力的能力较低，所以非自由场场地的超孔压比大于自由场场地的。

2.2 模型地基加速度反应

2.2.1 地表峰值加速度

自由场和非自由场计算工况中地铁车站结构上方地表监测点(A1～A4)和距离右侧墙不同水平距离的地表监测点(A6～A11)峰值加速度的如图7所示。

图7 地表不同位置峰值加速度Fig.7 Peak acceleration at different locations on the surface

由图7可知：水平地震动作用下，非自由场计算工况中地铁车站正上方地表峰值加速度较自由场工况中的地表加速度明显较小。其中，距离中心点为18 m处的监测点(A4)的峰值加速度减小幅度最大。此后，非自由场工况中的地表峰值加速度逐渐增加，距地表右侧墙18 m以外时，其加速度反应峰值又超过自由场计算工况的。这说明由于地下结构的存在，使得其上方一定范围的地表地震响应明显降低。

2.2.2 土体加速度反应

自由场和非自由场计算工况中距离地铁车站结构左侧墙5 m位置不同深度处土体的监测点(Aa～Ae)加速度放大系数如图8所示。由图8可知：两种计算工况下土体加速度放大系数自下而上先增大后减小，拐点出现在可液化土层，因此，在地震波的传播过程中，可液化土层具有一定的隔震效应；同时，非自由场工况下土体各监测点的加速度放大系数略小于自由场工况的，但相差很小，说明对上穿可液化土层的地下结构进行抗震设计时，对结构惯性力的施加仍可参照自由场的计算结果。

图8 不同工况下土体加速度放大系数Fig.8 Soil acceleration amplification coefficient under different working conditions

2.3 模型土体位移分析

自由场和非自由场计算工况下的模型土体在不同时刻的位移矢量如图9所示。可以看出：自由场工况中，地震动输入的前期阶段，土体基本为水平向运动，当地震动强度达到峰值以后，饱和粉细砂及以上土体出现上下方向的运动，此时，土体的运动不再仅限于水平向；非自由场工况中，激振初始阶段以水平向运动为主，随着孔隙水压力的不断积累，地铁车站结构两侧的土体开始向车站底部方向发生流动，车站底部土体因受到两侧土体的挤压及下部饱和粉细砂土体上升的孔隙水压力的作用而发生向上的位移，从而使得车站发生上浮。车站上浮的过程中，又会带动紧邻其两侧的土体产生向上的位移，从而地铁车站结构两侧的土体便产生不断的环向位移流动。地下结构上穿可液化土层时结构周围土体位移矢量分析可为提出抑制结构上浮措施提供有价值的参考数据。同时，激振结束后，自由场工况和非自由场工况中的可液化土层的最终水平位移分别为1.13 m和1.10 m，非自由场土体的残余变形稍大于自由场的，且地震波作用过程中亦是如此，说明地震时地下结构的存在可在一定程度上增加场地土层的变形。另外，自由场工况中同一深度处的土体位移基本相同，而非自由场工况中同一深度处的土体位移有一定差异，尤其是结构附近土层。

2.4 地铁车站结构应力反应分析

为分析可液化土层对上穿地铁车站结构应力反应的影响，表3给出了含有可液化土层及一般土层场地条件下的地铁车站结构侧墙和中柱监测点的最大、最小主应力幅值。其中，表中数据以受拉为正、受压为负。

由表3可知：含可液化土层工况中结构应力监测点的最大和最小主应力幅值均比一般土层工况中的要小，这说明可液化土层对上穿的地铁车站结构有一定的隔震效果；车站结构中柱始终处于受压状态，其最大压应力沿高度方向逐渐减小，且负二层中柱的最大压应力明显大于负一层中柱的值；而结构侧墙部分或是受拉、或是受压，负二层侧墙的拉压应力幅值较负一层侧墙的大；同时，侧墙与楼板的连接部位无论是最大主应力还是最小主应力都要大于侧墙其他位置，且侧墙底部的动应力要比顶部的动应力大很多，这是因为越是临近饱和粉细砂的土层，其地震变形越大，而此时结构需要承担的土层变形越大造成的。

2.5 地铁车站结构加速度反应分析

图10给出了含可液化土层和一般土层工况下的地铁车站结构中柱不同位置的峰值加速度沿其高度方向的变化曲线，其中AZ1、AZ2、AZ3、AZ4、AZ5、AZ6分别为负一层柱和负二层柱的柱顶、柱中、柱底的峰值加速度。由图11可知：两种计算工况下的结构柱子的峰值加速度沿柱高方向自下而上逐渐增大，结构此时处于弹性范围，而含可液化土层工况下的加速度变化更为均匀；与结构应力反应结果类似，和一般土层工况中的柱子峰值加速度相比，含可液化土层工况的柱子峰值小。

2.6 地铁车站结构横向变形分析

图11给出了含可液化土层和一般土层计算工况下地铁车站结构沿其高度方向的相对水平变形曲线。由图11可知：两种计算工况下的车站变形基本上均呈倒三角形分布，结构下方可液化土层没有改变其横向变形形式，但含可液化土层工况下的结构变形较一般土层小，其中含可液化土层7.5 mm，一般土层工况9.8 mm，这也从变形的角度证明了地震时结构下方的饱和粉细砂对上穿的地铁车站有一定的隔震效应。所以对该种工况下的地下结构采用传统的抗震设计方法进行设计时，其计算结果偏于保守。

图9 不同计算工况下研究区域位移矢量图Fig.9 Displacement vector diagram of the study area under different calculation conditions

表3 地铁车站结构主应力反应幅值

图10 中柱监测点峰值加速度Fig.10 Peak acceleration of central column monitoring point

图11 地铁车站结构的相对水平变形曲线Fig.11 Relative horizontal deformation curve of subway station structure

2.7 地铁车站结构上浮分析

图12给出了地铁车站结构底板不同位置(B1～B4)的上浮量随时间的变化曲线。由图12可知：在地震动输入的初始阶段，结构有少量的沉降，这是因为位于其正下方的饱和粉细砂震密下沉所致；随着地震动强度及持时的增加，孔压不断积累上升，结构上下方之间的压力差逐渐增大，使得结构开始上浮，并在11 s左右(峰值时刻)，上浮量急剧增加；之后随着地震动强度的减小，车站结构的上浮量逐渐降低。即地铁车站结构上穿可液化土层时，结构的竖向位移变化表现出“起始少量下沉，然后振荡上升，随后急剧上浮，最后缓慢下降”的发展阶段。同时，地铁车站底板不同位置的竖向位移变化量不同，其最大差值为8.97 mm，说明结构在地震过程中发生了一定的倾覆。对类似场地条件下的地下结构进行抗震设计时，应予以重视结构倾覆带来的影响。

地震作用结束后，自由场和非自由场工况下的数值模型的网格变形如图13所示。由图13可知：模型地基中可液化土层的存在，使得土体在激振结束后有一定的残余变形，且最大变形主要集中在饱和粉细砂层附近；模型地基的同等深度处，自由场计算工况中的网格变形大体一致，而非自由场计算工况中的网格变形则明显不同；临近车站两侧一定范围内的土体出现明显沉陷，而结构上方土体则先震密，而后在持续增加的孔隙水压力作用下逐渐上浮，因此，浅埋地下结构附近的土体部分上浮、部分沉陷可能会造成地表土体的开裂；另外，地铁车站上穿可液化土层时，地下结构附近土层的水平变形明显大于自由场工况下的变形，且变形也明显不均匀。所以，模型地基中存在可液化土层时，不宜用常规的反应位移法进行地下结构的抗震设计。

图12 地铁车站结构底板不同位置上浮位移Fig.12 Floating displacement of subway station structure floor at different positions

图13 激振结束数值模型网格变形图(放大200倍)Fig.13 Mesh deformation diagram of numerical model at the end of excitation (magnify 200 times)

3 结论

针对北京某典型箱型框架式地铁车站结构上穿一定厚度的可液化土层的工程实际，建立了土-地下结构相互作用模型，并与自由场工况的计算结果对比，研究了场地液化分布特征、地下结构的动力响应与上浮特征、周围场地位移沉降及矢量特征等地震反应规律，得到如下主要结论。

(1)地下结构上浮的过程中，其两侧土体会产生持续不断的环向位移流动；地震时地下结构的存在加大了可液化土体的地层变形，但会显著降低结构上方土体一定范围的地表地震响应；可液化土层中的孔压发展表现为“起始缓慢增长、最后急速增加至峰值保持一定时间，最后缓慢消散”的规律，孔压达到峰值的时刻与输入地震动的峰值时刻接近。

(2)与一般场地土层工况相比，上穿可液化土层时地铁车站结构的地震响应有所降低，下部可液化土层具有一定的隔震效应。

(3)地铁车站结构上穿可液化土层时，结构的竖向位移变化表现出“起始少量下沉，然后振荡上升，随后急剧上浮，最后缓慢下降”的发展阶段；液化场地中，浅埋地下结构附近的土体部分上浮、部分沉陷是造成地表土体开裂的内因。