随机降雨对滨海盐碱土壤水分分布的影响
郭爱科,武海霞,2,陶 涛,宋福如, 宋利强,宋聚强,王利书,2,程东娟,2
(1. 河北工程大学水利水电学院,河北 邯郸 056038;2. 河北省智慧水利重点实验室,河北 邯郸 056038; 3. 海河水利委员会漳河上游管理局,河北 邯郸 056038;4. 河北硅谷肥业有限公司,河北 邯郸 056038)
盐碱土是一种世界范围内的低产土壤,由于我国水土资源日益减少,实行节水灌溉、改良利用盐碱土是解决水土资源危机的重要措施[1]。盐碱土的水分分布状况直接决定其盐分分布规律,同时其土壤水分状况将影响灌溉制度的制定[2]。降雨作为土壤水分动态变化的重要驱动因素,其随机时程分配特性是导致降雨入渗过程以及作物灌溉需水动态过程中不确定性产生的直接原因[3]。揭示由随机降雨引起的土壤水分变化特征,研究其演变机理,分析降雨特性对其影响程度,对于合理制定节水灌溉制度、掌握盐碱土壤水分分布动态规律等方面具有重要实际意义与理论价值。
降雨对水文循环过程的研究至关重要,尤其是土壤水分空间分布规律的研究。刘汗等[4]通过比较不同降雨强度下的土壤入渗性能,认为土壤水分入渗性能随着降雨强度的增加而降低。葛波等[5]通过分析不同降雨等级下各层土壤含水率对降雨事件的响应,结果表明浅层土壤含水率与降雨量变化趋势具有良好的同步性。白盛元等[6]研究了不同降雨量级对土壤剖面含水率的影响,研究结果认为土壤水分的垂直输送具有滞后性,降雨对土壤水分的补给效果随深度而减弱。目前关于降雨对土壤水分分布影响的研究较多,但学者们通常将自然降雨事件概化为均匀降雨过程,对于考虑降雨事件随机性的研究较少。
通常利用降雨单元的随机时程分配特性描述降雨过程的随机性,Rodrguez-Iturbe等[7-8]提出基于Poisson过程表示降雨事件的随机特性。Rodrguez-Iturbe等[9]首先在日尺度以下的随机降雨模拟中引入矩形脉冲理论,提出Neyman-Scott矩形脉冲降雨模型。Fowler等[10]基于Neyman-Scott矩形脉冲降雨模型,利用蒙特卡洛抽样法预测了英国约克郡30年内的气候变化情况。Mimeau等[11]利用Neyman-Scott矩形脉冲降雨模型模拟了地中海区域土壤含水率对随机降雨的响应。如上所述,目前国内学者对于普通降雨特征对土壤水分的影响进行了诸多探讨,但降雨过程的随机性如何影响土壤水分分布状况,降雨随机时程分配特征对不同土层土壤水分的影响程度,当前研究关注较少。
综上所述,为揭示降雨过程的随机性对土壤水分的影响,以降雨总量、降雨次数与极端降雨量级为降雨特性,采用Neyman-Scott矩形脉冲模型模拟随机视角下的降雨过程,进而驱动HYDRUS模型分析土壤水分分布特征,应用析因设计方差分析方法量化降雨总量、降雨次数、极端降雨量级以及其时程分配特征对土壤水分的影响,并扩展性地讨论了相较降雨特征变化,HYDRUS模型参数的不确定性对土壤水分的影响。
1 研究区概况与研究方法
1.1 研究区概况
研究区域为河北省黄骅市典型盐碱地,地形为滨海平原,气候属于暖温带大陆性季风气候,冬春雨雪稀少,夏季降雨量占全年降雨总量的75%,年均降雨总量为627.8 mm,最大年降雨总量为937.0 mm,最小年降雨总量为303.6 mm。土壤类型主要为潮土、盐化潮土和沼泽化潮土,盐碱地占耕地面积69%。土壤含盐量为0.2%~2%,为硫酸盐氯化物盐土[12]。
1.2 基于Neyman-Scott矩形脉冲(NSRP)模型的降雨模拟
一次完整的降雨事件可划分为若干连续的不同长度的时段,各时段内降雨强度相同,相邻时段间雨强不同。研究表明,该降雨事件的特征可通过若干基本的降雨单元进行模拟[13-15]。鉴于此,Rodriguez-Iturbe等[16]基于点过程理论,引入Neyman-Scott矩形脉冲模拟降雨过程。该模型本质为簇生点过程模型,可采用少量参数表示降雨过程及其潜在的物理现象[17]。模型中随机变量服从的分布、参数及其单位如表1。

表1 NSRP模型随机变量分布及参数Table 1 Distribution and parameters of stochastic variables of NSRP model
1.3 基于HYDRUS模型的土壤水分入渗模拟
1.3.1 HYDRUS模型概述 HYDRUS模型已被广泛应用于分析水流与溶质在非饱和介质中的运移过程。模型在非饱和水流中使用经典的Richards方程来描述一维垂直或水平水流运动:
(1)
式中,h为负压水头(mm),θ为土壤体积含水率(mm3·mm-3),K为水力传导系数(mm·h-1),t为入渗时间(h),z为垂向坐标轴,向上为正(mm)。
土壤水分特征曲线是反映土壤基质势与含水率之间关系的重要水力参数。HYDRUS软件中分别提供了VG(Van genuchten)模型、BC(Brooks and Corey)模型以及Kosugi模型用于拟合土壤水分特征曲线,本文采用应用广泛的VG模型,其方程为:
(2)
(3)
式中,KS为饱和导水率(mm·h-1),θr为土壤残余含水率(mm3·mm-3),θs为土壤饱和含水率(mm3·mm-3),α为进气吸力的倒数(mm-1),n为孔径分布参数,m为水分特征曲线参数。
1.3.2 初始条件与边界条件 本次研究模拟土壤深度为150 cm,为分析逐小时尺度下降雨入渗情况,模型模拟时段设置为72 h,模拟时间步长为小时。为便于分析不同土层深度下降雨综合特性对土壤水分入渗的影响,根据不同土层土壤水分标准差与变异系数将土壤剖面概化为4层,0~20 cm为活跃层(变异系数35%~40%和标准差9~10),20~60 cm为次活跃层(变异系数20%~35%和标准差6~9),60~100 cm为相对稳定层(变异系数10%~20%和标准差1~6),100~150 cm为稳定层(变异系数<10%和标准差<1)[18]。
初始条件:初始体积含水率(θ0)为15.67%(mm3·mm-3)。
θ(z,0)=θ0(z)
(4)
上边界:模型上边界条件设置为考虑积水的大气通量边界,最大积水深度为10 cm。上边界输入变量为考虑随机时程分配的降雨方案。
(5)
式中,K为土体边界层的导水率(mm·h-1);q为入渗补给量,即降雨强度(mm·h-1);hf为土体表层积水深度(mm);dh/dt为土体表面蓄水引起的水量的变化量(mm·h-1)。HYDRUS模型设定入渗率开始减小时刻为积水点,到达积水点后上边界转变为变水头边界,地表积水高度由于降雨而增加,因入渗而降低。
下边界:研究区域地下水位埋深平均为7 m,下边界可概化为自由排水边界。
1.3.3 模型参数率定 基于HYDRUS-1D模型自带的Rosetta模块,输入土壤质地与容重,可初步得到土壤水分特性参数,然后通过一维垂直积水入渗试验实测数据进行参数率定。入渗试验土柱选用厚1 cm的PVC管,土柱内径为7 cm,高60 cm;填装土壤取自黄骅市盐碱地试验田,经风干后过2 mm筛,装填高度为50 cm,装填容重为1.4 g·cm-3,试验重复3次。PVC管侧均匀分布10个直径为2 mm的小孔,插入传感器测定不同时刻下土壤含水率,马氏瓶控制供水水头为5 cm左右。率定后的VG模型参数结果如表2。
为验证模型参数的准确性,以率定后的VG模型参数(表2)为HYDRUS模型的初始土壤水分特性参数并建立模型,模型初始条件与边界条件与反演试验一致。由图1可以看出,率定的模型参数很好地模拟了盐碱土壤水分入渗下土壤含水率的变化,且模拟值与实测值非常接近,其中模拟结束后各土层含水率与对应的实测值的皮尔逊相关系数(R)为0.997,表明经率定后的HYDRUS模型参数可作为随机降雨入渗模型的参数。

图1 HYDRUS-1D模型参数模拟值与实测值对比Fig.1 Comparison of simulation and measurement of HYDRUS-1D model parameters

表2 率定后的Van genuchten模型参数Table 2 Calibrated Van genuchten model parameters
1.4 基于随机时程分配的降雨方案设计
采用三水平析因设计方法设计研究地区降雨方案,研究表明,黄骅市年降雨主要集中在夏季,且极端降雨量级以40~60 mm·h-1为主[19]。本文基于黄骅市2010—2020年实测逐时降雨资料,在Matlab软件环境下,采用Monte Carlo方法以及NSRP降雨过程随机模拟模型,以降雨总量(A)、降雨次数(B)、极端降雨量级(C)为实验因子,每个因子设置高中低3个方案,两两组合形成27个方案。其中,以各个方案中降雨总量、降雨次数以及极端降雨量级为约束条件,采用Monte Carlo方法随机模拟每个方案100次(即重复数为100),以此表征降雨过程的随机性,具体方案设置见表3。

表3 基于随机时程分配的降雨方案设计Table 3 Rainfall scheme design based on stochastic time and degree distribution of rainfall
2 结果与分析
2.1 降雨资料分析与模拟结果
以黄骅地区2001—2010年7月实测的逐时降雨资料为基准,在Matlab软件环境下,采用矩法估计NSRP模型参数,结果见表4。

表4 黄骅地区降雨资料的统计学参数及NSRP模型参数Table 4 Statistical parameters of rainfall data and parameters of NSRP model
基于黄骅地区NSRP降雨模型,采用Monte Carlo法,随机生成不同降雨总量、降雨次数、极端降雨约束下的多场降雨过程。以降雨总量为200 mm(A2方案)、降雨次数为15场(B2方案)与极端降雨量级分别为40 mm·h-1(C1方案)、50 mm·h-1(C2方案)、60 mm·h-1(C3方案)为例,随机模拟5场降雨过程,结果如图2所示。
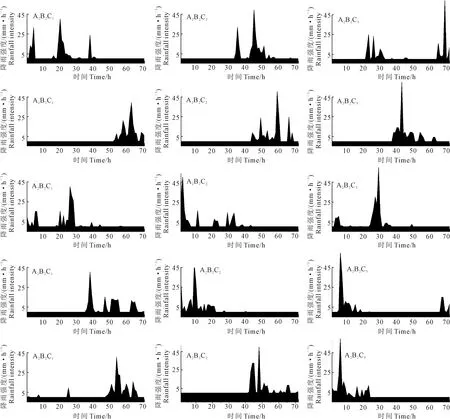
图2 小时尺度下随机降雨实践模拟结果(以极端降雨的3个水平为例)Fig.2 Simulation results of random rainfall practice on hourly scale (taking three levels of extreme rainfall as an example)
2.2 降雨总量、降雨次数、极端降雨及随机时程分配对土壤含水率的影响
表5为采用析因设计方差分析方法分析降雨总量、降雨次数、极端降雨及随机时程分配对土壤含水率的影响结果。由表5可以看出,与降雨过程的随机性影响相比,降雨总量和降雨次数对各土层含水率均存在极显著影响(P<0.01),而极端降雨仅对次活跃层影响显著(P<0.05);对比F值发现降雨总量对除活跃层外的土层含水率影响远大于降雨次数与极端降雨。降雨总量与次数间二阶交互作用对除去表层土壤的其余土层含水率影响显著,而3种因素三阶交互作用(A×B×C)对土壤含水率不存在显著影响。

表5 降雨总量、降雨次数以及极端降雨对各土层含水率的影响Table 5 Effects of rainfall, rainfall frequency, extreme rainfall and their interactions on soil moisture
2.3 降雨次数、极端降雨及随机时程分配对土壤含水率的影响
由于降雨总量对土壤含水率的影响最大,因此有必要在控制降雨总量的影响下,进一步分析降雨次数、极端降雨与降雨时程分配对不同土层土壤含水率的影响。此时,若控制降雨总量,则降雨次数一定程度上可反映雨强的大小。
表6为不同降雨总量下,降雨次数与极端降雨相较降雨过程的随机性对土壤含水率的影响。与2.2节所得结果相似,降雨次数对土壤含水率影响显著,且该影响随着降雨总量的变化呈现一定的差异;极端降雨对土壤含水率的影响则呈一定的随机性,即降雨总量为160 mm时,极端降雨对活跃层土壤含水率影响显著,降雨总量为200 mm时,其对次活跃层土壤含水率影响显著。
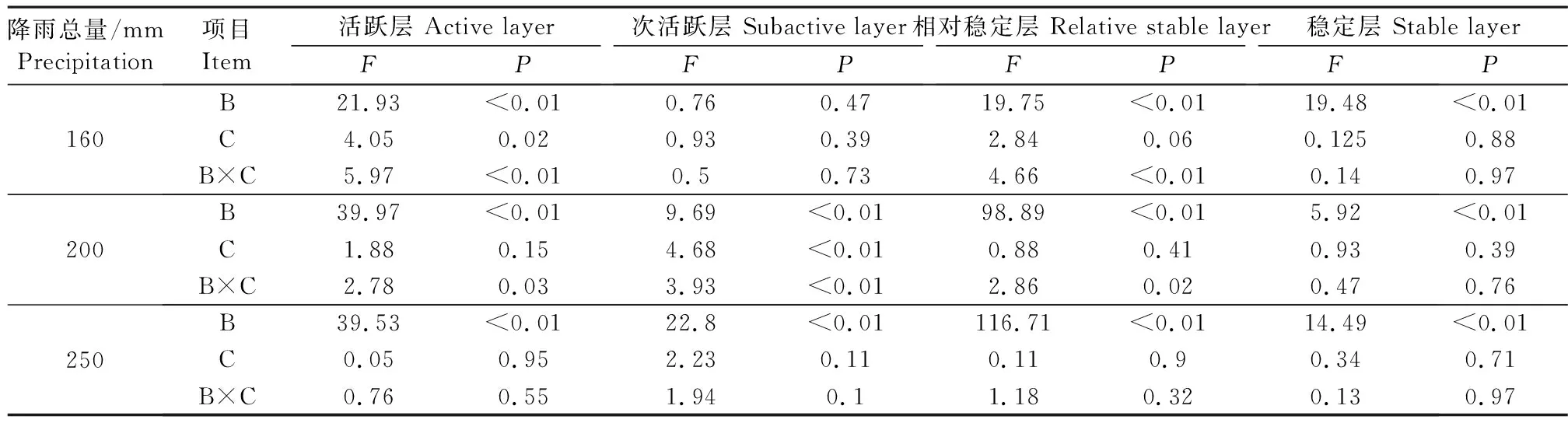
表6 降雨次数与极端降雨对不同降雨量下各土层土壤含水率的影响方差分析Table 6 Variance analysis of influence of rainfall frequency and extreme rainfall on soil moisture content of different soil layers under different rainfall
整体来看,降雨次数对土壤含水率的影响较极端降雨更大。究其原因,土壤含水率在不同土层上的运移是连续的时间过程,单次的极端降雨事件对土壤含水率的空间运移影响小于持续多次的降雨事件。为进一步分析其原因,以降雨总量为160 mm为例,计算了不同降雨次数与不同极端降雨组合下,不同土层土壤含水率情况,结果见表7。
由表7可知,当降雨次数较低(10次)时,其平均降雨强度较大,相较于降雨次数较高时(15、20次),表层土壤含水率增高2.74%~6.23%,而相对稳定层土壤含水率降低5.66%~15.63%,这与鲍彪等[20]的研究结果一致;对于活跃层土壤而言,降雨次数为10次、极端降雨量级为40 mm·h-1时土壤含水率最大,但相对稳定层土壤含水率最小。

表7 降雨总量160 mm时降雨次数与极端降雨对各土层含水率的影响Table 7 Effects of rainfall times and extreme rainfall on water content of soil layer unde 160 mm rainfall
2.4 随机降雨与均匀降雨入渗对土壤含水率影响的对比分析
除去降雨总量、降雨次数与极端降雨对土壤含水率的影响外,仍需明晰降雨过程的随机性相较均匀降雨过程对不同土层土壤含水率影响程度的差异。由此,设降雨总量、降雨次数与随机降雨在相同水平下的均匀降雨方案,即不考虑降雨的随机时程分配,而将降雨总量按降雨次数均匀分布于研究时段内。
如图3所示,均匀降雨的降雨单元均匀分配于整个降雨过程,位于降雨过程后半段的降雨量由于响应时间较短无法及时入渗至土壤深层;而随机降雨的降雨单元可能聚集于降雨过程的前半部分,因此随机降雨在降雨总量为160 mm与200 mm时可入渗至深层土壤。当降雨总量较大(250 mm)时,均匀降雨下的深层土壤含水率相较随机降雨最大可增高39.51%,其原因可能在于:其一,降雨总量增大时,均匀降雨的降雨强度均匀增加,较大的降雨强度缩短了位于后半段降雨的入渗滞后时间,李小璐等[21]研究结果同样表明在一定的降雨总量下,降雨强度越大,入渗滞后时间越短;其二:随机降雨内部由于分配不均引起的极端降雨导致表层土壤较易达到饱和,从而使得水分入渗速率在较短时间内降至饱和导水率,从而使得深层土壤含水率较小。

注:图中活跃层、次活跃层、相对稳定层及稳定层为按照土壤垂向水分变异系数划分的土层深度。Note: The active layer, subactive layer, relatively stable layer and stable layer in the figure are the soil depth divided according to the soil vertical water variation coefficient。图3 不同降雨总量、降雨次数随机降雨与均匀降雨下不同土层土壤含水率Fig.3 Soil water content of different soil layers under stochastic rainfall and uniform rainfall under different total rainfall amount and rainfall frequency
通过比较两种降雨方式下各土层含水率可知(表8),随机降雨与均匀降雨入渗对浅层土壤含水率影响的差异较小,但随着土层深度的增大,两种降雨方式下土壤含水率的差异不断增大。在降雨总量为160 mm,降雨次数为15、20次时,相较于均匀降雨,随机降雨下相对稳定层土壤含水率较大(增量为32.83%、22.91%)。在降雨总量较大时,随机降雨条件下稳定层土壤含水率均相对降低,降低幅度最高达39.52%(降雨总量为250 mm,降雨次数为20)。
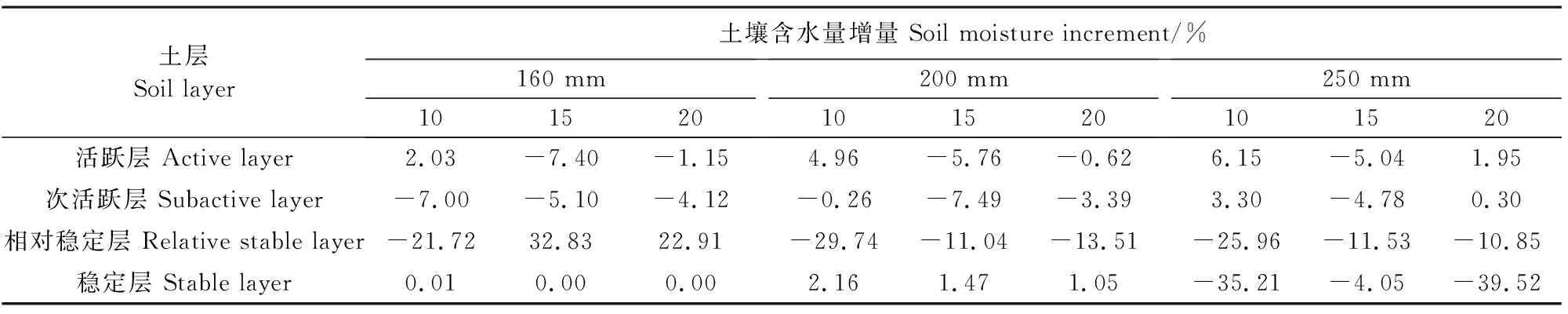
表8 随机降雨与均匀降雨下土壤含水率的差异Table 8 Difference of soil water content under stochastic rainfall and uniform rainfall
3 讨 论
降雨是影响土壤水分入渗变化最为直接的因素。以往众多研究表明[22-24],土壤水分的入渗主要由降雨总量和降雨强度决定,且不同土层水分分布还与降雨时程分配特征有关。本研究采用定量的析因设计方差分析方法分析降雨综合特性对土壤水分的影响,与以往研究结论[25]一致,相较降雨时程分配的随机性,降雨总量是影响降雨入渗后土壤水分分布状况的主要因素,降雨次数(即平均降雨强度)次之,极端降雨影响较小。
此外,有研究表明[26-27],土壤含水率除受降雨影响外,土壤水力特性参数对其影响同样值得关注。为进一步明晰土壤水力特性与降雨特性对土壤含水率的影响差异,且避免模型参数的不确定性对研究结果的影响,笔者扩展讨论了HYDRUS模型中VG模型的敏感性参数土壤饱和含水率(θs)、土壤孔径分布参数(n)与降雨总量对土壤含水率的影响程度。
以率定参数n、θs为基础,对其与降雨总量分别施加±5%的扰动,分析不同土层土壤含水率的变化情况,结果见表9。由表可知,参数θs和降雨总量对所有土层含水率影响均极显著(P<0.01),参数n对于活跃层与次活跃层土壤含水率影响显著,这与张海阔等[28]的研究结论一致。同时,值得注意的是,活跃层土壤含水率受参数θs的影响最大,参数n的影响次之,降雨总量影响最小。综上,土壤水分的运移研究过程中,模型参数的不确定性不容忽视。

表9 降雨总量与VG模型参数(n,θs)对不同深度土壤含水率的影响Table 9 Effects of total rainfall and VG model parameters(n,θs) on soil moisture content at different depths
4 结 论
本文以滨海盐碱土为研究对象,分析了降雨总量、降雨次数、极端降雨量以及其随机时程分配特征对土壤水分分布过程的影响,并讨论了模型参数不确定性与降雨特征相比对土壤水分分布的影响差异,取得了以下结论:
1)整体来看,相较降雨过程的随机性而言,降雨对土壤含水率的影响因素:降雨总量(A)>降雨次数(B)>极端降雨量(C),且降雨总量与次数间二阶交互作用对土壤含水率影响显著(P<0.05)。
2)降雨总量一定时,当降雨次数较低(10次)时,其平均降雨强度较大,相较于降雨次数较高(15、20次)时,表层土壤含水率增大2.74%~6.23%,而相对稳定层土壤含水率降低5.66%~15.63%。
3)随机降雨与均匀降雨对浅层土壤含水率影响的差异较小,但随着土层加深,两种降雨方式下土壤含水率的差异不断增大,当降雨总量为250 mm时,均匀降雨条件下的稳定层土壤含水率相较于随机降雨最大增高39.52%,且相比于均匀降雨过程,随机降雨在降雨总量较小(160 mm与200 mm)时可入渗至稳定层。
4)在较浅的土层尤其表层土壤含水率受到HYDRUS模型参数θs(土壤饱和含水率)与n(孔径分布参数)的影响要远大于降雨总量,因此,在采用HYDRUS模型模拟土壤水分分布时,应重视土壤水力参数的不确定性影响。

