机器学习模型在地下水埋深模拟中的适应性分析

牛欣怡，鲁程鹏，卢佳赟，吴成城，刘 波，束龙仓

(河海大学水文水资源学院，江苏 南京 210098)

1972年，我国地下水开采量为196亿m3左右，至2014年末，地下水开采量已达到1 117亿m3，约为1972年的6倍，在北方一些缺水的地区，如河北、北京、河南等地，其地下水供水量已达到总供水量的70%左右[1]。由于地下水的超量开采，导致很多地区出现海水入侵、地面塌陷、地下水干旱等严重的地质和生态问题[2-5]。准确模拟地下水埋深对于地下水合理开发利用和保护具有重要的指导意义[6]。地下水模拟模型大体分为物理模型和数据驱动模型[7]。基于详细的水文地质资料构建的物理模型主要有具有物理意义的MODFLOW、GMS等数值模型，但是物理模型在求解过程中具有工作量大、时间长、模型校准复杂等缺点[8-9]。人工神经网络等数据驱动模型可以轻松逼近物理系统的复杂行为和响应，并且能够在短时间内优化不同约束集的大量案例场景。相比于物理模型中较多的假设条件、复杂的输入变量和参数精确校准等问题，数据驱动模型的输入变量更易测量和量化，数据限制更低，模型参数适用性更强，而且模拟时间也比较短[10]。因此，机器学习这类数据驱动模型在埋深模拟中前景广泛，尤其是在缺少水文地质勘测资料的地区，是不可替代的。

支持向量机(support vector machines，SVM)、循环神经网络(recurrent neural network，RNN)和长短期记忆神经网络(long short-term memory，LSTM)是目前在地下水埋深模拟方面应用最广泛的机器学习模型，但由于SVM模型和RNN模型是基于不同的理论构建，导致其在模拟效果方面有一定的差异[11-14]。目前国内学者在研究基于机器学习模拟地下水方面主要集中在单一模型的改进和应用，如闫佰忠等[15-16]基于多变量LSTM模型模拟监测井的地下水水位，并与单变量LSTM、反向传播神经网络模拟结果对比；张钧泳等[17]建立不同参数的SVM模型，探讨单因子、多因子建模反演地下水埋深精度问题；张文鸽等[18]结合混沌优化方法，构建基于混沌优化的峰值识别最小二乘支持向量机模型，模拟义长灌区地下水位，并将结果与最小二乘支持向量机模拟结果进行比较。然而，对于同一地区，对基于不同理论方法的模拟效果进行比较，尤其是适应性方面的研究比较少。

本文采用SVM模型、RNN模型和LSTM模型进行地下水埋深模拟，通过模拟京津冀平原地区13个城市地下水埋深情况，比较3种模型的模拟精度和适应性，并将3种模型应用到随机选择的6个测站，以验证更适用于地下水埋深模拟的机器学习模型，以期为今后地下水埋深模拟模型选择以及参数调整提供参考。

1 模型构建

1.1 地下水埋深模拟模型框架

本文气象(降水、平均气温、平均风速)和地下水埋深数据分别来自中国气象数据网记录的24个气象观测站和各地区711个地下水监测站实测的2005—2018年168个月的日观测数据，基于月均值利用普通克里金法插值得到京津冀13个城市的相应月数据。社会经济类要素(人口、经济生产总值)和地下水开采量来源于各个城市相应年份经济年鉴的年值，为了计算方便，均匀分配到各月。随后构建RNN模型、LSTM模型和SVM模型。在输入变量方面，虽然以多变量因素作为输入比单变量好[19]，但是当因素与地下水相关性较弱时，反而会成为一种噪声影响模型的模拟精度[20-22]。为了提高地下水埋深模拟模型的准确性，基于Pearson相关系数去除与地下水位相关性不显著的变量[23-24]。随后将显著因素和上月地下水埋深作为输入变量进入模型训练。为了保证能够得到较好的训练，防止模型对训练数据的过度拟合，将样本按照时间顺序以训练数据与测试数据为11∶3划分。最后在京津冀地区随机选择6个测站的上月埋深和显著因素作为输入变量进入训练好的模型中验证。以上过程通过ArcGIS 10.3.1和Python3.6实现，模型框架图见图1。

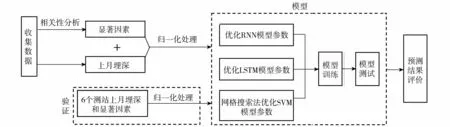
图1 地下水模拟模型框架Fig.1 Framework diagram of groundwater simulation model

1.2 SVM

SVM模型是以统计理论为基础，主要的应用方向是分类、回归。SVM法的特点是在小样本问题及低维空间数据集不可分的前提下，将其映射到高维空间，从而达到可分的效果[25]，该数据处理方式相对于神经网络可以从很大程度上避免学习或局部极值的出现[26]。SVM法的回归计算如下。

首先给定一组训练样本M={(x1，y1)，(x2，y2)，…，(xn，yn)}，(xi，yi)∈R(i=1,2,…，n)。以简单线性式表示：

f(x)=wx+b

(1)

其中x=(x1，…，xn)w=(w1，…，wn)b=(b1，…，bn)

式中：x为特征向量；w为超平面的法向量；b为位移向量。这两个因素决定超平面的方向。

寻找最小的w来保证式(1)的平坦。假设在一定精度的δ下，训练样本所有数据都可以用式(1)拟合，则可将问题转化为凸优化解决：

(2)

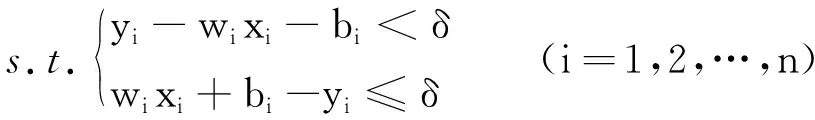
(3)

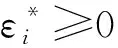
(4)

约束条件：

(5)

式中A为正则化常数，用来衡量回归函数的平坦度。再通过拉格朗日乘数法求解，转化成对偶问题。

(6)

对于非线性问题来说，最后公式表示为

(7)

式中K(xi，xj)表示各种核函数如线性核、高斯核等。

1.3 RNN

RNN模型被专门设计用来捕捉时间序列数据中固有的结构[14]，在模型中是通过传递隐藏层神经元的输出或者状态来实现这一点，这些神经元代表了在之前时间步骤中学习到的东西，并且作为下一个时间步骤的额外输入[27]。RNN模型中的计算式可以写为

ht=tanh(Wxt+Uht-1+c)

(8)

yt=Vht+c

(9)

式中：ht为隐藏状态；yt为输出向量；xt为输入向量；W、U、V分别为输入、隐藏和输出权值；c为偏置。RNN模型的训练采用时间反向传递，基于神经网络的权值和之前隐藏状态的误差梯度来调整网络权值。由于梯度在这一过程可以呈指数变化，因此它们往往会消失或者爆炸[28]。学者们针对这一问题，又对RNN模型进行优化，提出了长短期记忆神经网络模型。

LSTM模型是RNN模型改进的一种类型，LSTM模型架构在不激活函数的情况下，在隐藏单元状态之间强制执行恒定误差流，从而将梯度问题最小化。LSTM单元包含3个作为门的乘法单元：遗忘门、输入门和输出门[29]。因为每个门都是神经元，它可以通过传递输入、反向传播误差和调整权重的过程来学习哪些输入和细胞状态对模拟输出是重要的。

1.4 数据归一化处理

在模型输入和输出中，由于不同类型的数据存在着极端值和较多的噪音，需要进行归一化处理来消除异常值和极端值的影响，以此来使模型中寻求最优解的过程变得平缓，加快梯度下降的速度，并且提高模型精度[30-31]，本文采用线性归一化对数据进行处理：

(10)

式中：z为原始数据；z*为无量纲化后的数据；zmax、zmin分别为原始数据中的最大最小值。

1.5 模型评价指标

本文采用确定系数R2、均方根误差RMSE、平均绝对百分比误差MAPE[32]、纳什效率系数NSE对3种模型模拟效果进行评价。

2 模型实例对比分析

2.1 相关性分析

地下水埋深与影响因素之间的相关性如表1所示。京津冀地区中大部分地区主要影响地下水埋深的因素是人口、经济、开采量和降雨，其中人口、经济、开采量的相关性系数都比较高，大体上都达到0.5以上，而降水的相关系数大多保持在0.3左右，由此可以看出人类活动对于地下水埋深的影响占主导地位，自然因素的影响占比较小。从表1可以看出，除了天津、廊坊、沧州，北京和河北大部分城市地下水埋深和开采量呈现负相关，出现这种情况的主要原因是在研究期间地下水开采量虽然逐年减少，但是总量相对较大。如北京市、河北省年均开采量基本保持在20亿m3、140亿m3左右，且地下水埋深的恢复具有一定的时间滞后性，因此从表面上看开采量逐年减少，地下水埋深逐年增大，但实际上地下水埋深增大的速率在逐渐减小。而天津的年开采量在5亿m3左右，当开采量减少时，地下水埋深恢复效果更显著。

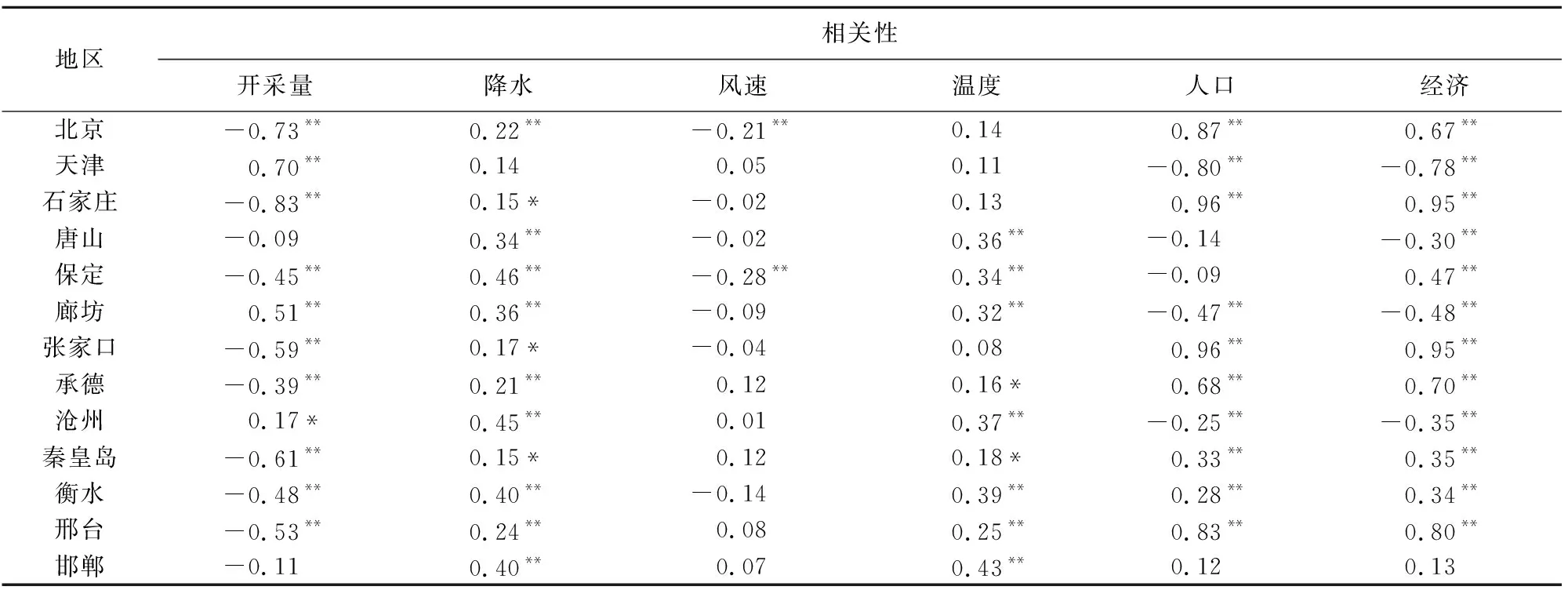
表1 京津冀13个城市地下水埋深与多变量之间的相关性

2.2 模拟结果分析

基于RNN模型、LSTM模型、SVM模型得到的结果用R2、RMSE、MAPE、NSE指标进行评价，结果见表2，相应的4个误差指标箱型图见图2，模型运行时间见图3。

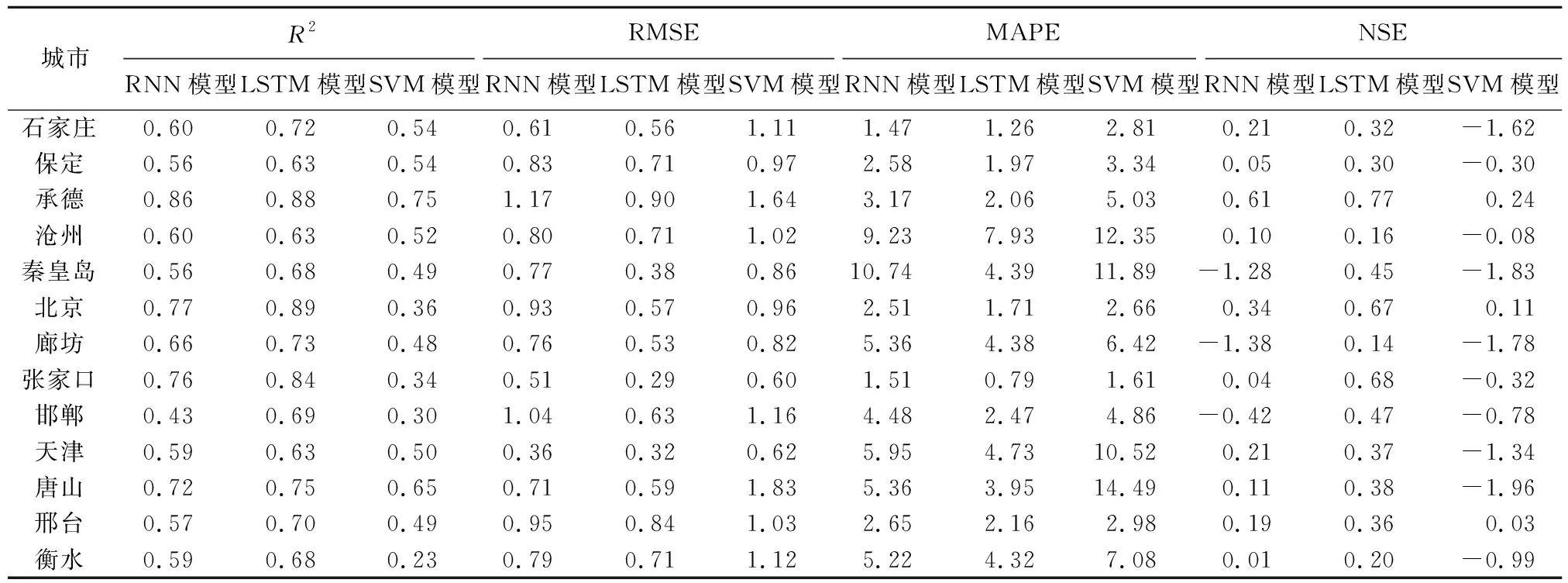
表2 3种模型性能指标结果

图2 不同模型模拟误差指标分布箱型图Fig.2 Boxplots of simulation error indexes of groundwater depth simulation with three models

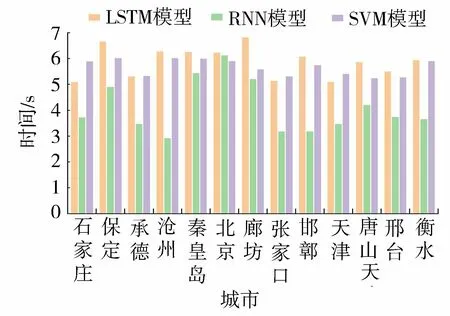
图3 京津冀13个城市地下水模型运行时间Fig.3 Running time of three models applied in 13 cities of Beijing-Tianjin-Hebei

由表2可知，LSTM模型的拟合精度最高，其次是RNN模型，SVM模型表现最差。LSTM模型的拟合精度始终保持在0.6～0.9之间，最大为0.89，最小为0.63，均具有高度相关性，其中有54%地下水埋深数据的拟合度在0.6～0.7，23%的数据拟合度在0.8～0.9之间。利用RNN模型进行模拟的城市一半以上地下水埋深拟合度在0.5～0.6之间，拟合度在0.8～0.9的数据仅占8%。而基于SVM模型进行模拟的城市中，有62%的城市地下水埋深拟合精度在0.2～0.5之间，相关性较低。从图2(a)可以明显看出LSTM模型箱型图分布宽度最窄，SVM箱型图分布宽度最宽，这体现了LSTM模型应用在不同城市的适应性在3个模型中是最好的。

从RMSE、MAPE和NSE 3项指标来看，不同城市模型的误差排序从大到小均为SVM模型、RNN模型、LSTM模型。结合3项误差的箱型图可以明显看出，在不同的指标下，LSTM模型的箱型图分布最窄，SVM箱型图分布最宽。在RMSE和NSE两个指标下RNN模型虽然与LSTM模型分布宽度相差不大，但是均出现异常值，而且异常点的个数比LSTM模型多，这是因为RNN模型存在梯度消失或爆炸问题，而LSTM模型可以克服这些问题，使模型运行得更加稳定，从而误差波动范围也小。在3个指标下，SVM模型箱型图分布宽度均大于RNN模型，这是信息流在模型中传递的方向导致，RNN模型具有记忆功能，信息流在模型中是双向传递，而SVM模型中信息流仅仅只是单向传递。综合上述模型指标的结果显示，LSTM模型的泛化能力明显比RNN模型、SVM模型优秀。

从图3可以看出LSTM模型运行时间和SVM模型运行时间基本一致，保持在5.5 s左右，LSTM模型和SVM模型运行时间长但波动较小，RNN模型运行时间最短但波动范围最大。出现这种情况的原因除了上文提到的LSTM模型可以消除RNN模型中的梯度消失和爆炸问题外，SVM模型运行时间和LSTM模型运行时间基本一致的原因是SVM模型运行时间包括参数调整和模拟两部分，其中由于SVM模型过多的核函数和相应的参数导致参数调整的时间过长，而SVM模型在模拟部分的时间比较短，是其他模型运行时间的1/10。

3 模型参数适应性和稳定性分析

3.1 参数适应性

在模型应用中，针对不同地区的情况需要适当地进行参数调整，对于SVM模型，由于人工搜索参数存在较大的误差，因此本文采用网格搜索法[33]对SVM参数进行搜索，得到模型应用在各城市的参数，见表3。

从表3可以看出，虽然13个城市所处的地理位置和气候条件不同，但是在利用模型模拟时有相似之处。RNN模型模拟13个城市的地下水埋深，除张家口、邯郸、衡水的学习率为0.001外，其他城市学习率均为0.01，隐藏层的神经元数量全部保持在30以内，并且数量为30和10的城市占大多数，共达9个，迭代次数大部分都是1 000和1 500；在LSTM模型下学习率均为0.001，隐藏层神经元除了邯郸、天津、衡水、邢台，其他城市均为30，迭代次数除了保定、天津、衡水，其他均为1 500次。除此之外，也可以明显看出张家口、邯郸的RNN模型和LSTM模型的参数完全一样，但是由于LSTM模型比RNN模型更能消除梯度爆炸等因素，导致RMSE和MAPE都比RNN模型小，使得模拟结果更加精确；在SVM模型下，石家庄、保定、沧州、秦皇岛和衡水5个城市选择的是rbf函数，北京、廊坊、邯郸、天津、邢台选择的是sigmoid函数，承德、唐山选择的是linear函数，仅有张家口选择的是多项式函数。

表3 不同城市地下水埋深模拟的模型参数

综合上述3个方面，在13个城市中，LSTM模型变动参数最少，运用参数为5组；SVM模型运用参数次之，运用的参数共达9组；RNN模型运用的参数最多，达到10组。但是从参数变量上来看，SVM模型参数变量最多，应用的核函数有4个，再包括C和g一共有6个参数，是其他两个模型的2倍，因此虽然SVM模型应用的参数组数少，但是根据其模型运行时间来看，其适应性程度低于RNN模型。所以在考虑模型参数的适应性以及精确程度方面，首选LSTM模型，其次是RNN模型，最后是SVM模型。

3.2 模拟稳定性

为了验证RNN模型、LSTM模型、SVM模型模拟的稳定性，随机选择了京津冀地区6个测站进行地下水埋深模拟，讨论3个模型在新测站的适应性情况，模拟结果如图4所示，随后采用R2、RMSE、NSE指标评价模拟结果，相关参数和指标计算结果见表4。

表4 6个测站埋深模拟参数和误差指标

由图4可以直观看出，基于LSTM模型模拟的地下水埋深和实测值拟合效果最好，其次是RNN模型、SVM模型。对于LSTM模型来说，其基本能够将埋深的每个转折趋势很好地模拟出来。表4结果显示，LSTM模型在6个站的拟合精度都达到0.9以上，RMSE最小，NSE基本都达到0.8以上，表明该模型是可靠的。RNN模型模拟效果相比于LSTM模型来说，转折和峰值表现效果比较差，如宋桥站、高公庄站、郑庄子和捷地站，甚至高公庄和捷地的NSE指标为负值，表明模型的结果不可信。对于SVM模型来说，只能将埋深的变化趋势大致描述出来，在细节方面忽略比较多，这是由于SVM模型中没有记忆功能导致的。而且SVM模型的NSE系数除了宋桥站，其他均为负数，且比RNN模型大得多，表明SVM模型在模拟华北平原大部分城市或测站的浅层地下水埋深时稳定性差。这是因为传统的机器学习方法在模拟地下水埋深与输入变量之间的关系方面有限，当输入变量较多时循环神经网络结构可以更好地整合多特征输入和输出变量之间的非线性关系[34-35]。

从参数的适应性角度来看，6个测站的地下水埋深模拟中，LSTM模型仅利用1组参数，RNN模型利用2组参数，而SVM模型利用了6组参数，这也表明LSTM模型的适应性最优。

4 结 论

a.在京津冀地区13个城市的地下水埋深模拟中，LSTM模型模拟效果最好，其次是RNN模型，SVM模型最差，主要原因在于RNN模型具有保留记忆的功能，可以从隐藏神经元中提取信息，而LSTM模型在此基础上进一步解决了梯度消失的问题，但SVM模型只能从与因变量密切相关的数据中提取特征，当处理稍长的数据集时，无法解决数据间的长期依赖问题。在运行时间方面，RNN模型最短，LSTM模型其次，SVM模型由于参数过多，运行时间最长。

b.在参数适应性方面，不同城市基于LSTM模型进行模拟时调整的参数最少，虽然RNN模型和SVM模型应用的参数组数相似，但是由于SVM模型有过多的核函数，因此RNN模型参数适应性较好。

c.将3个模型分别应用到随机选择的6个测站中进行验证，结果表明LSTM模型适应性最好，不仅R2高达0.9以上，NSE也达到0.8以上，6个测站仅应用了1组参数；RNN模型效果其次，SVM模型效果最差，6个测站中有5个测站的NSE为负值，没有成功应用。