一种相位截断傅里叶变换非对称光学压缩加密系统

郭媛，吴兰兰，敬世伟

（齐齐哈尔大学计算机与控制工程学院，黑龙江 齐齐哈尔 161006）

0 引言

美国学者REFREGIER P 和JAVIDI B［1］于1995年提出双随机相位编码（Double Random Phase Encoding，DRPE）光学加密系统，使光学图像加密技术得到快速发展。最近，JMV A［2］提出一种使用非线性联合变换相关因子来实现双随机相位编码的光学安全技术。TAO Yuanchun［3］提出一种明文关联鬼成像加密系统，将参数密钥用椭圆曲线加密，降低密钥空间且提高系统抗攻击能力。ABD-EL-ATTY B［4］提出一种基于量子游走和双随机相位编码技术的新型光学加密，在两个加密阶段使用替代量子漫游（Alternate Quantum Walks，AQW）抵抗来自数字和量子计算机攻击。WW A［5］提出一种通过相位优化生成可信的纯相位全息图方法，用于隐写光学图像加密；利用菲涅尔域优化随机相位和相位约束下改进的两步迭代傅里叶变换算法，计算出全息图，为光学图像提供了一种全息加密新方法。传统DRPE 系统是线性对称光学加密系统，加密密钥和解密密钥相同，安全性得不到保障。PENG W Q［6］于2010年提出一种基于PTFT 的非对称密码体制，在加密过程中采用相位截断方式得到解密密钥，打破算法的线性运算，实现了加密密钥与解密密钥的分离，系统安全性有了很大提高。2011年WANG X 提出基于PTFT 图像加密算法的安全增强算法［7］，在原来的光学加密系统频谱域中加入一个振幅掩膜。2012年WANG X 等［8-9］利用密文和两个公钥这两个约束条件，仅需两步迭代傅里叶变换，便可恢复PTFT 系统的私钥信息，攻破PTFT 加密系统。针对这个问题，有很多学者对PTFT 系统进行改进，2013年DING Xiangling 等［10］在原来PTFT 系统的输入图像前添加一块不公开的随机相位掩膜，达到扰乱输入图像空间的效果，破坏傅里叶迭代算法的约束条件。2014年WANG X 用一种新的攻击算法振幅-相位迭代恢复算法［11］攻破了2011年的安全增强算法［7］，2015年GAO Xiong［12］针对幅相迭代恢复算法提出对原来的振幅模板的分布进行调整，设计一种特殊的振幅掩膜板，在原来PTFT 加密系统中将调整后的振幅模板放在傅里叶频谱面上来提高抗攻击性。此算法虽然安全性提升了，但密文的直方图和相邻相关性分布图不均匀，系统统计特性不好。同时以上加密算法密文体积大，特别是非对称加密，解密密钥与明文一样大小，且无法运用混沌代替，使得传输量进一步加大。2021年XU Zhao 等针对基本PTFT 系统提出一种深度学习攻击算法［13］，通过以残差网络为基础训练大量的明密文对使神经网络拟合明文和密文之间的对应关系，训练大量手写数字图像后攻破PTFT 加密系统，使密文图像基本恢复。

综上，PTFT 算法提出至今，虽然实现了非线性光学加密，但仍然存在抗攻击性差的问题，特别是随着深度学习算法的出现，使PTFT 系受到了更大的攻击威胁。另外，PTFT 加密系统在信息传输时，除了传输一组密文信息外，还需传输两组截取的振幅（相位）信息，信息的传输量增大三倍，传输效率大大降低，运算时间复杂度高。

针对上述问题，本文设计的系统一方面在原来的PTFT 加密系统第一块相位掩膜后又加了一块特殊阈值设定的振幅掩膜，用部分振幅截断后保留的相位角作为最终密文，破坏了迭代直接得到全部振幅的可能，使加密系统安全性得到了保证，且密文直方图和相邻相关性分布均匀。另一方面本文提出用压缩感知［14-17］对明文图像进行预处理，运用离散小波变换将图像高低频信息分离，将待加密图像压缩至明文图像的1/4，且有效保留高频信息，减小密文密钥传输体积，缩小传输量节省加密时间。

1 压缩加密原理

可加密系统由图像压缩和PTFT 非对称加密两部分构成，如图1。

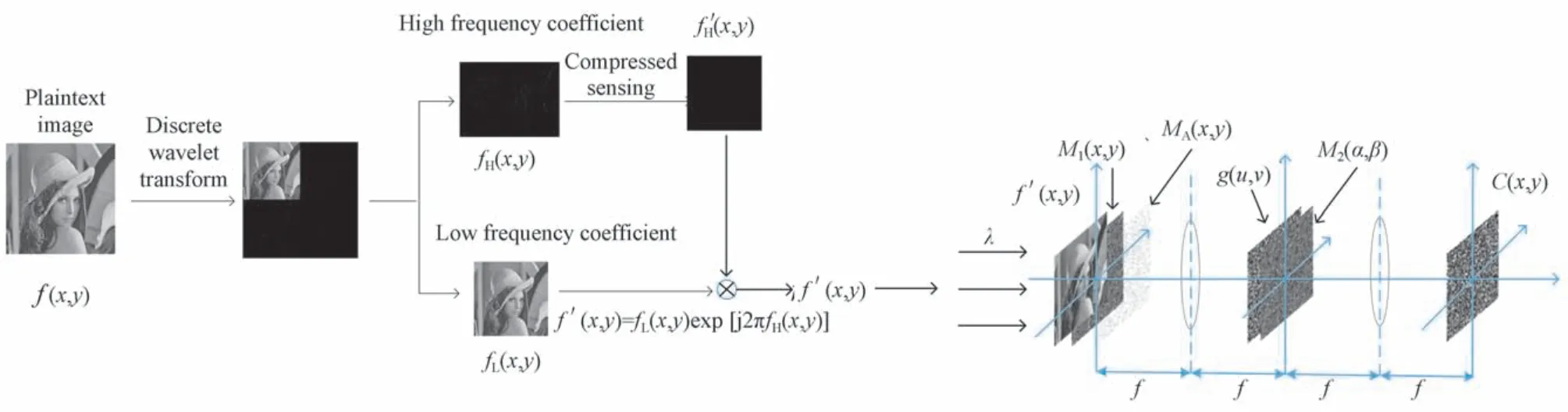
图1 PTFT 光学压缩加密系统工作原理Fig.1 Working principle of PTFT optical compression encryption system

图像压缩部分先将明文图像进行离散小波变换，分为低频系数和高频系数，再将高频部分用压缩感知压缩至原大小的1/3，并以相位形式融入低频系数，构造大小为明文图像1/4 的待加密复数图像。图像高低频的分离及高频信息压缩以相位形式共同构造复图像，不但可以更好地保存明文图像有效信息，高质量重构图像，而且有效减少图像传输量，用时更少、效率更高。

本文PTFT 非对称加密部分在基本PTFT 系统基础上于第一块相位模板后增加一块振幅模板。复数图像经过相位-振幅模板双重调制后经过透镜进行一次傅里叶变换，取得部分振幅用作私钥一，相位角作为中间值受到第二块相位掩膜的调制后再进行一次傅里叶逆变换，取得振幅用作私钥二，相位角作为最终密文，有效抵抗两步迭代傅里叶变换等多种算法攻击，抗攻击性好，灰度直方图及相邻像素相关性分布更均匀。

2 算法描述

本文加密系统工作流程如图2。

图2 基于压缩感知的PTFT 系统加密流程Fig.2 Encryption flowchart of PTFT system based on compressed sensing

1）首先对明文图像f(x，y)进行离散小波变换，将图像分为低频系数fL(x，y)和高频系数fH(x，y)，用压缩感知将高频系数压缩为原来的1/3 并以相位形式融入低频系数，构造一个大小为明文图像1/4 的待加密复图像f'(x，y)，即

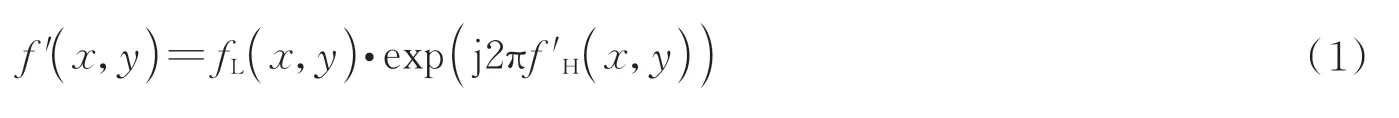
2）设(x，y)为空域坐标系，(α，β)为频域坐标系，f'(x，y)经相位模板M1(x，y)和振幅模板MA(x，y)的双重调制，再进行傅里叶变换后截取部分振幅D1用作私钥给用户保存，保留相位g(u，v)作为中间值进一步调制。

式中，f'(x，y)为压缩后的复数图像，M1(x，y)=exp{j2πφ(x，y)}和M2(α，β)=exp{j2πϕ(α，β)}为两个相位模板，PT{ }为截取振幅操作，PR{ }为相位保留操作，FT{ }表示傅里叶变换，MA(x，y)是根据M1(x，y)而产生的阈值thr再进行赋值而得到的振幅模板，r设定为0.8。

3）g(u，v)经相位模板M2(α，β)的调制，再进行傅里叶逆变换，截取部分振幅D2为私钥二保存，相位保留取其相位角为最终密文C(x，y)。

式中，IFT{ }表示逆傅里叶变换，arg{ }为取相位角操作。

解密流程和加密流程相反，解密流程如图3。

图3 基于压缩感知的PTFT 系统解密流程Fig.3 Decryption flow of PTFT system based on compressed sensing

1）密文C(x，y)转化为相位形式后和私钥二D2相乘，经傅里叶变换后与M2(α，β)的复共轭M2*(α，β)=exp{-j2πϕ(α，β)}相乘保留相位g(u，v)。

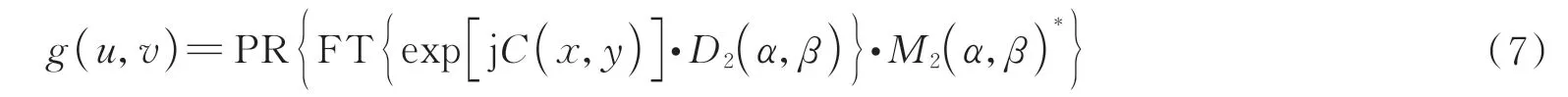
2）g(u，v)与私钥一D1相乘后经傅里叶逆变换，乘以MA(x，y)的逆振幅调制器MA*(x，y)和M1(x，y)的复共轭M1*(x，y)得到正确的复图像f'(x，y)。

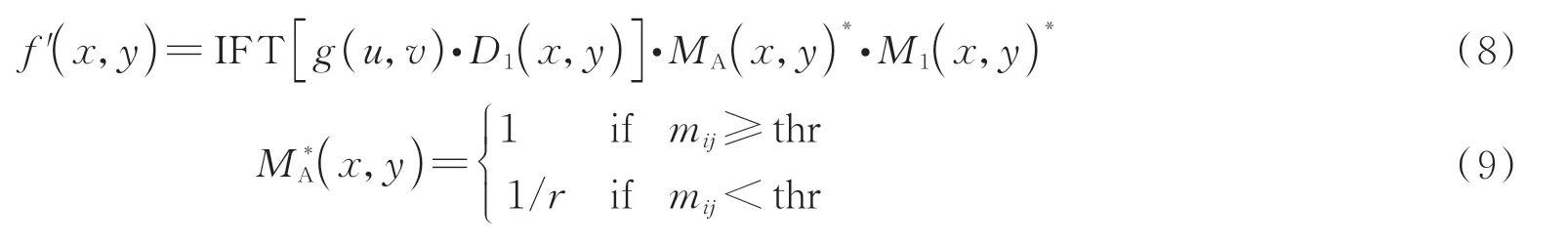
3）复图像f'(x，y)提取振幅和相位，相位角除以2π 后作为高频系数fH'(x，y)，振幅作为低频系数fL(x，y)，高频系数通过正交匹配追踪算法（Orthogonal Matching Pursuit Algorithm，OMP）［18-19］进行重构恢复初始的高频系数fH(x，y)。

4）再将恢复的高频系数fH(x，y)和拆分的低频系数fL(x，y)进行离散小波逆变换，得到明文图像f(x，y)。

3 系统特性实验

为验证加密系统的可行性和安全性，选用不同种类的5 幅灰度图像在Python3.7 和Pycharm 环境下进行实验，加解密效果如图4。

图4 加密系统的加解密图像Fig.4 Encryption and decryption image of the encryption system

由图4可见，无论是二值图像、医学图像，还是对比度不同的其他灰度图像，密文图像大小均为明文图像的1/4，且加密图像完全掩盖明文图像的信息，解密图像恢复质量好。

3.1 统计特性分析

3.1.1 灰度直方图

灰度直方图反映图像像素值统计特性，加密图像直方图应尽量均匀与明文图像直方图分布差异较大。本文对明文图像，截断振幅用作密文图像，及相位角用作密文图像和解密图像对比，如图5所示。

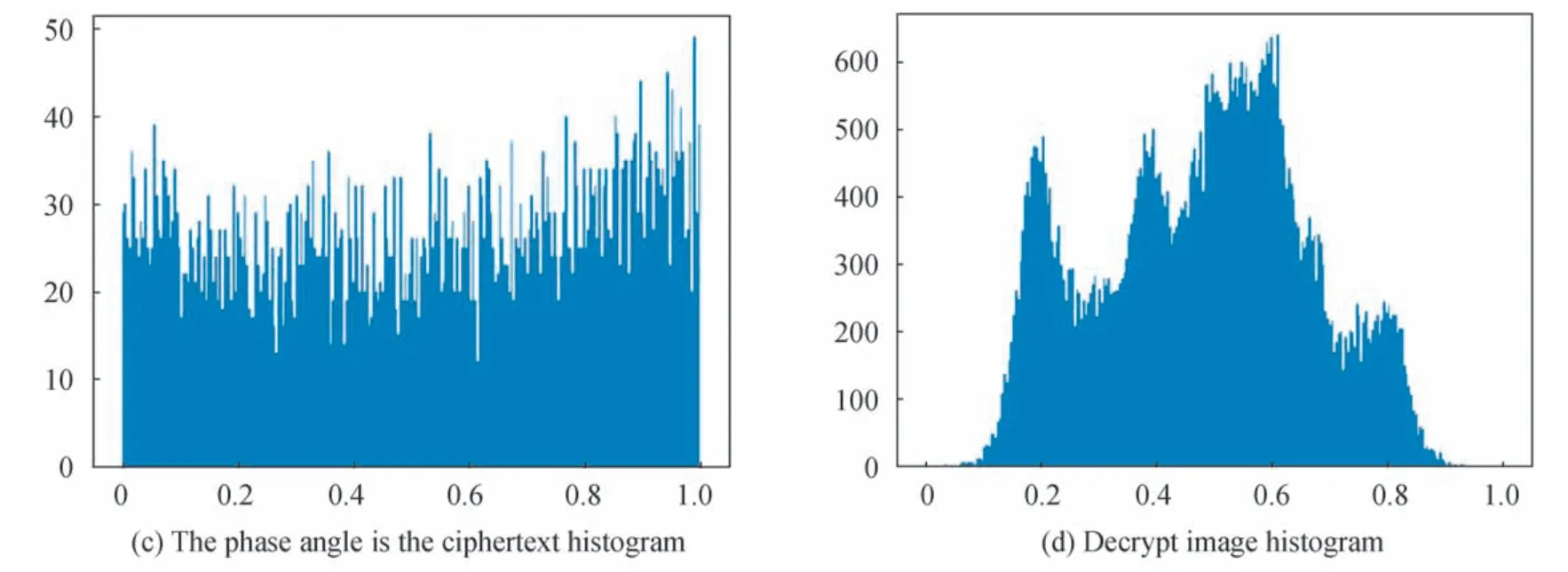
图5 灰度直方图Fig.5 Grayscale histogram

由图5可见，明文图像和解密图像的灰度值分布不均匀，呈现出明显的分布规律，不管是振幅作为密文还是相位角作为密文直方图都和明文直方图差距明显，本文提出相位角作为密文直方图分布更均匀，更好隐藏明文图像信息。

3.1.2 相邻像素相关性

好的加密方法应对相邻像素相关性具有较强的破坏作用，相邻像素相关性越低，相邻像素相关图越散，系统越安全。

图6是水平方向相邻像素相关性分布图，可见明文图像和解密图像明显相关性较强，提出的以相位角作为密文的分布比以振幅为密文的分布图更散，相关性破坏地更彻底。

图6 相邻像素相关性分布Fig.6 Correlation distribution of adjacent pixels

表1中明文图像的水平、垂直和对角的相邻系数都接近于1，而本文提出的相位角作为密文的相关系数更接近于0，效果比振幅作为密文好。

表1 相关系数分析Table 1 Correlation coefficient analysis

3.2 压缩重构质量对比分析

为测试本文压缩后重构质量，与文献［14］压缩方式作对比，具体效果如图7。

图7 不同压缩方式不同比例重构图像Fig.7 The reconstructed image with different compression methods and different scales

由图7可见，压缩相同比例，本文压缩至明文图像1/4 后重构图像比文献［14］压缩至明文图像1/4 后重构图像质量好很多，本文压缩至1/4 甚至比文献［14］压缩至4/5 重构质量更好。

表2可见，本文压缩至明文图像的1/4 后重构图像与明文图像的峰值信噪比（Peak Signal-to-noise Ratio，PSNR）比文献［14］压缩至明文图像的4/5 后重构图像与明文图像的PSNR 更高，说明本文压缩方式图像恢复质量好。

表2 不同方式压缩不同比例的峰值信噪比Table 2 Different methods of compressing different ratios of peak signal-to-noise ratio

3.3 加密时间及传输量对比分析

为测试本文系统加密时间与传输量，选取文献［7，10，12］作对比，结果如表3。

由表3可见，本文加密系统耗时缩短了3～4 倍，压缩加密使加密过程传输量大大减小，存储空间缩小，运算速度大幅提高。

表3 时间以及密钥传输量对比分析Table 3 Comparative analysis of time and key transmission volume

4 抗攻击实验

4.1 抗两步迭代傅里叶变换攻击

传统PTFT 非对称加密系统不能抵御两步迭代傅里叶变换的攻击，当迭代次数为300 次时，加密图像可破解。本文方法和传统PTFT 加密方法抗两步迭代傅里叶攻击结果如图8。

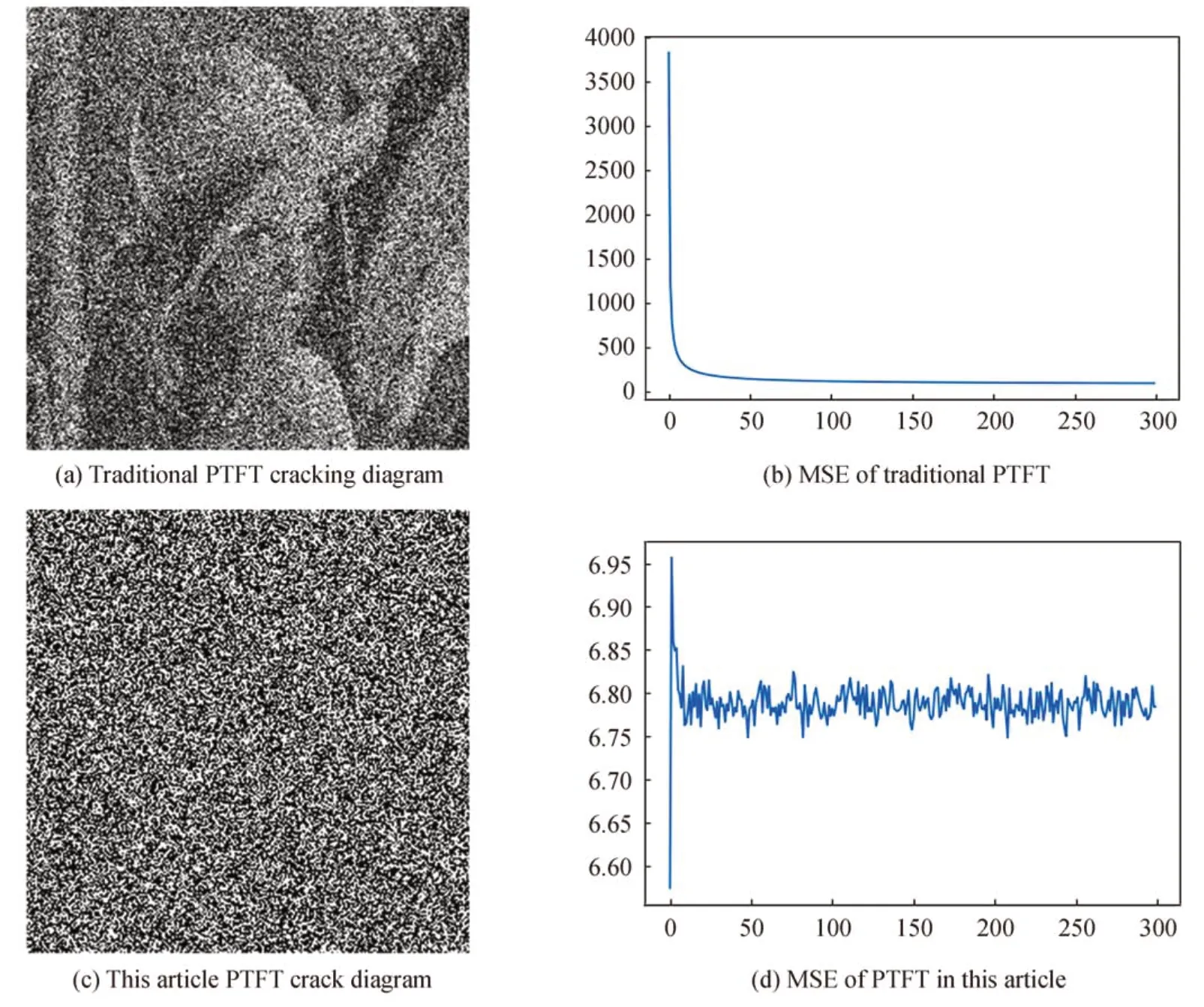
图8 攻击破解对比图和均方误差（MSE）对比图Fig.8 Comparison diagram of attack cracking and Mean Square Error（MSE）comparison chart

图8（a）为传统PTFT 加密系统经300 次迭代攻击的破解结果，可分辨出明文“lena”图像，图8（c）为本文增加振幅掩膜后的PTFT 加密系统，同样经过300 次迭代攻击，无法得到原始图像轮廓，说明本文算法可有效抵御两步迭代傅里叶变换攻击。图8（b）和图8（d）分别是为传统PTFT 加密系统和本文加密系统迭代次数与MSE 值的关系曲线。图8（b）MSE 值随迭代次数的增加而趋向于平行，通过傅里叶变换的迭代运算，逐步逼近私钥信息的近似值，破解图可以看出明文图像“lena”的轮廓，而图8（d）在300 次迭代中MSE 曲线不收敛，获取不到私钥信息，破解图完全看不出明文图像的信息，本文PTFT 系统可有效抵抗两步迭代傅里叶算法攻击。

4.2 抗深度学习方法攻击

文献［13］提出了一种基于深度学习的PTFT 攻击方法，用基于残差网络ResNet 的神经网络训练10 000张明密文对，网络自动学习密文到明文的拟合过程，训练后用手写数字图像进行测试，图像基本恢复，表明可完全攻破传统的PTFT 加密系统。此方法攻击本文PTFT 系统，分别用10 000 张64×64 的二值图像、医学图像和不同对比度灰度图像进行训练测试，结果如图9。

图9中，（a）～（d）为被攻击明文图像，（e）～（f）为密文图像，（i）～（l）为各明文攻击破解图。（i）为传统PTFT 系统经深度学习攻击破解后解密图像，可见，解密图像与明文图像基本一致。（j）～（l）为本文PTFT 系统经深度学习攻击后解密图像，可见，二值图像、医学图像和灰度图像经深度学习方法攻击后解密图像与明文图像相差甚大，解密图像完全看不出明文图像的信息，说明文献［13］的深度学习的攻击方法并不能攻破本文PTFT 加密系统。

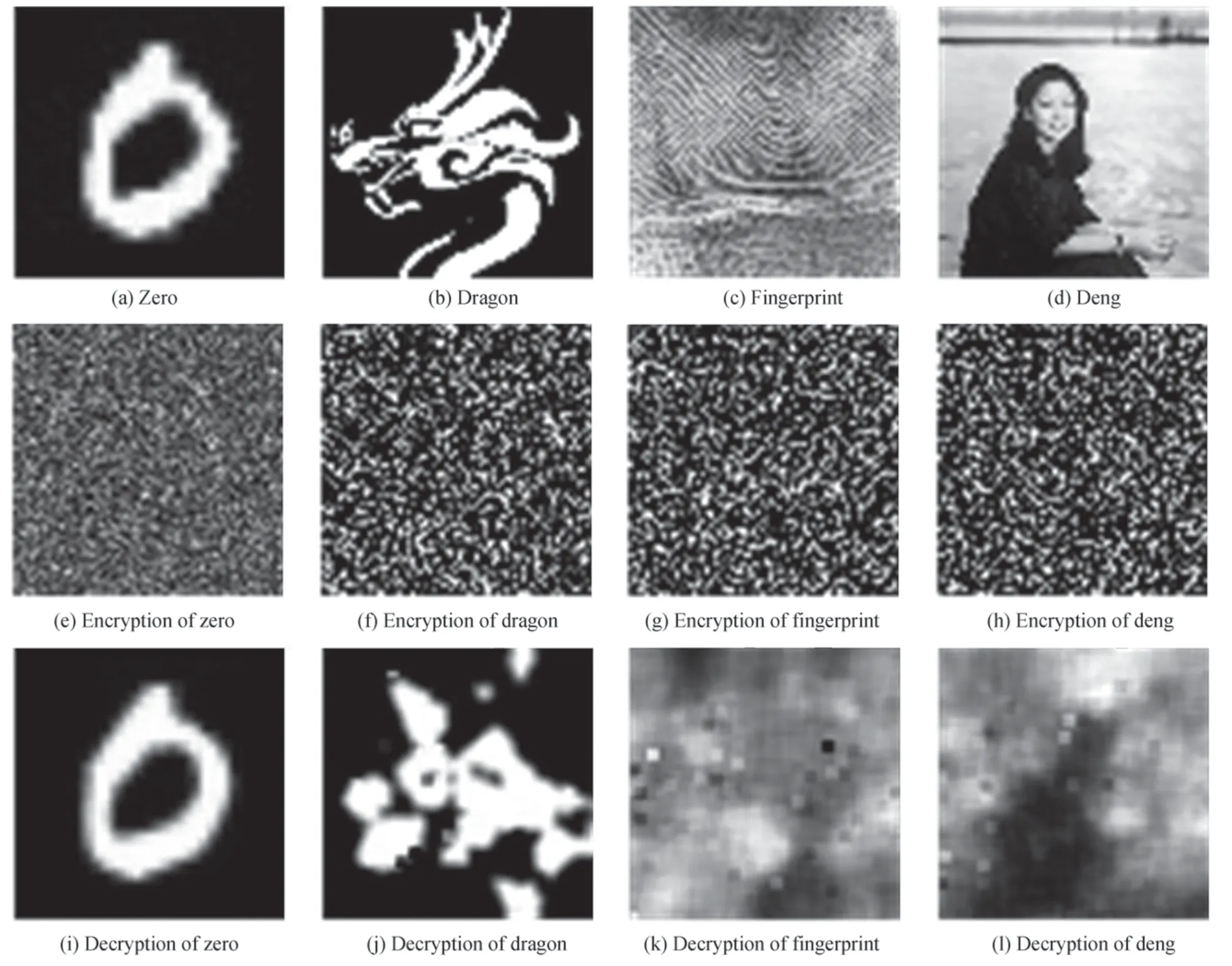
图9 攻击破解图Fig.9 Comparison diagram of attack cracking

4.3 抗噪声攻击

为测试本文加密系统的抗噪声攻击性能力，分别为密文添加不同强度的椒盐噪声和高斯噪声，解密效果如图10～11。

图10四幅图像分别是添加不同噪声比例的椒盐噪声后的解密图像，噪声比例越大解密图像越模糊，图11四幅图像分别是添加均值为0，不同方差的高斯噪声后的解密图像，方差越大，解密图像越模糊，当椒盐噪声比例为0.1 和高斯噪声方差为0.3 时仍能分辨出明文图像，可见本文加密系统抗噪声攻击高。

图10 不同噪声比例下椒盐噪声干扰的解密图像Fig.10 Decrypted images of salt and pepper noise interference under different noise ratios

图11 不同方差下高斯噪声干扰的解密图像Fig.11 Decrypted images with Gaussian noise interference under different variances

4.4 抗剪切攻击

抗剪切攻击也是衡量一个加密系统的抗攻击性能高低的一个指标，本文光学图像加密系统进行抗剪切攻击能力测试，结果如图12。

图12 剪切不同尺寸的加密图像和解密图像Fig.12 Cut encrypted and decrypted images of different sizes

如图12，图（a）、（b）表明图像不同位置任意剪切大小为1/16 或1/4，解密效果依旧好。图（c）尽管剪切密文图像的1/2，但还是能从解密图像看出明文图像“lena”的轮廓，输出图像较好地保留了明文信息，本文的光学加密算法抗剪切攻击能力高。

4.5 选择明文攻击

针对加密系统的攻击主要有选择明文攻击、已知明文攻击、选择密文攻击和唯密文攻击。而选择明文攻击对加密系统最具有威胁性，若本文加密系统能抵抗此攻击，那么完全可以抵抗另外三种攻击。

图13中P1为256×256 全0 的明文图像，P2为只改变P1其中一个像素值的图像，P3=|P1-P2|，C1和C2分别为P1和P2加密后的加密图像，C3=|C1-C2|。从图中可以看出C3完全获取不到明文图像的任何信息，可见本文提出的加密算法完全抵抗选择明文攻击。

图13 选择明文攻击效果图Fig.13 Selected plaintext attack effect diagram

5 结论

本文将压缩感知与PTFT 非对称加密相结合，用压缩感知对明文图像经小波分离的高频信息压缩2/3，使其作为低频信息的相位信息，最终将明文图像压缩至1/4，不仅缩短加密时间、减小密钥传输量，且在相同重构算法下重构质量提高5.2 dB。在原系统第一块相位模板后增加一块振幅模板，并保留相位信息作为中间传输信息且将相位角作为最终密文，将两次截取的部分振幅作为两组私钥，有效提高系统对各种攻击算法的抵抗能力，保障系统安全性。将相位信息作为密文，密文分布更加均匀，抗统计特性更好。