基于统计平均方法实现透过散射介质全息成像
张辉,张在坤,孔德鹏,贺正权
(1 中国科学院西安光学精密机械研究所,西安 710119)
(2 中国科学院大学,北京 100049)
0 引言
散射介质广泛存在于日常生活中,例如生物组织、火灾烟雾、毛玻璃、浑浊的深海、空气中的大雾等。散射介质内部复杂的折射率及反射率分布会使光线改变其原有的传播方向,导致光电成像系统在散射环境下无法正常工作。目前,在智能驾驶、气象学、生物医学诊断、深海探测等领域,透过散射介质对目标物体进行清晰成像的应用需求越来越广泛,透过散射介质成像在医学、安全、民生等方面具有重要的意义[1]。
光束在经过散射介质透射或反射时,由于散射介质折射率的不均匀性,成像光束携带的目标信息在成像面上表现为明暗点随机分布的散斑。但在这一散射过程中,物体的信息并没有丢失,而是重新分布,因此出射散斑场仍然携带着原始物体的信息[2]。通过散斑场获取物体信息以实现物体的图像重建一直是研究人员重点关注的一个问题,各种新技术被应用于解决散射介质成像的问题,例如光学相干断层扫描技术[3-6]、鬼成像技术[7-9]、飞行时间技术[10]、自适应光学技术[11]、相位共轭技术[12-13]、波前整形技术[14-15]、基于光学传输矩阵的测量技术[16]、基于光学记忆效应的散射介质成像技术[17]等。然而鬼成像技术需要将已知的散斑清晰地照在物体上才能恢复在探测端的成像路径上被散射介质破坏的信息。波前整形技术需利用空间光调制器(Spatial Light Modulator,SLM)或数字微镜器件对入射光波前进行相位或振幅上的补偿,扫描和运算较为复杂,且每种整形方案只适用于一种散射场景,普适性较低。后来人们提出了传输矩阵法来弥补波前校正技术的不足,该方法将获取到的散斑场结合散射介质的传输矩阵来实现成像,但是传输矩阵的获取难度大,且易受噪声干扰,严重影响图像的恢复质量。近年来,全息光学的应用为解决散射介质成像问题提供了新的技术方案,目标图像的模糊是由散射介质造成的相位信息损失导致,而全息术可以恢复在传统摄影中因强度记录而丢失的相位信息。2014年,SINGH A K 等[18]提出了一种基于数字全息实现透过散射介质及拐角处成像的方法,该方法只需对CCD 接收到的干涉散斑场进行一次简单的傅里叶变换即可恢复出目标物体图像,但该方法需要旋转散射介质进行散斑平均,应用场景有限。2016年,MICHAEL J 等[19]对该方法进行改进,通过增加一个散射介质实现透过双散射介质成像,但物光与参考光先干涉后透过两个散射介质,导致CCD 接收到的光强很弱,干涉图像获取困难,且易受到环境光等其他因素影响,重建图像质量不稳定。
本文通过统计平均方法和无透镜傅里叶变换数字全息技术从散斑场中检索出物体信息。物光透过散射介质后再与参考光干涉,通过旋转的散射介质平均散斑场,消除由散射介质引入的随机相位,结合傅里叶变换重建物体图像。在旋转的散射介质后加入一个静置的散射介质,使参考光在物光透过两个散射介质后与其干涉,这种方法不仅可以拓展成像系统的应用场景,还可以解决先干涉后透过散射介质成像方法光强不足的问题。实验探究了毛玻璃旋转速度以及CCD 曝光时间对重建图像峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)的影响,以实现最佳成像效果。
1 基于统计平均方法透过单个散射介质成像
1.1 基本原理
透过单个散射介质成像光路如图1所示。由激光器发出的激光经扩束器(Laser Beam Expander,LBE)和衰减片A 后,激光通过分束器(Beam Splitter,BS)分为两束光,一束通过成像目标作为物光,另一束经过反射镜Mirror 入射到凸透镜Lens 上,光束经凸透镜Lens 将平面波转化为球面波后汇聚于P点作为记录参考点光源。其中,物体到BS2 的距离等于P点到BS2 的距离以保证参考光源与物体处于同一平面内,满足无透镜傅里叶变换数字全息的记录条件。参考光和物光散斑光场由合束器BS2 合束后干涉,最终由精确聚焦在BS2 表面的CCD 相机接收散斑干涉图像。
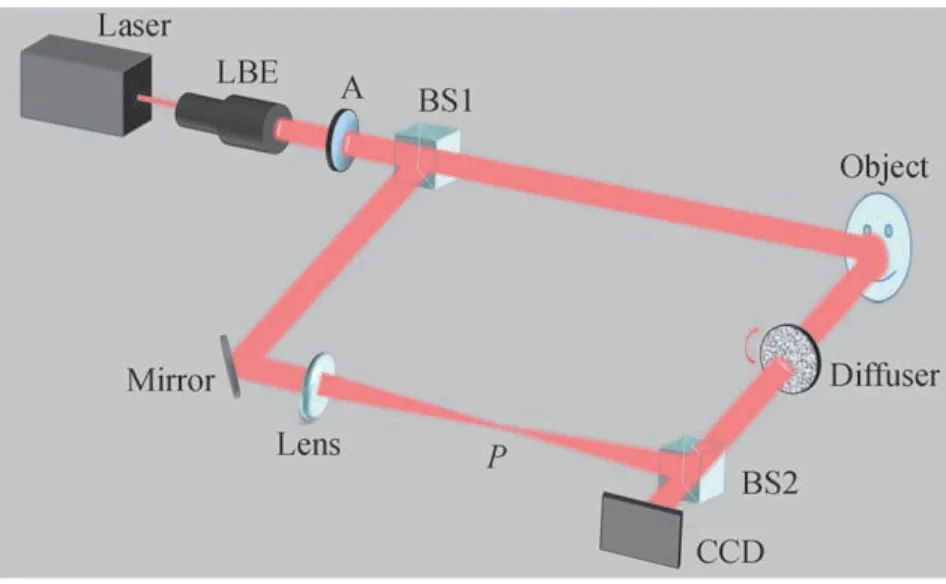
图1 透过单散射介质成像实验光路Fig.1 Optical path diagram of imaging experiment through a scattering medium
当物光场经过散射介质毛玻璃Diffuser 时,成像光束携带的目标信息被扰乱为随机分布的散斑图像,引入的随机相位可表示为ϕr(ξ,η)。设uo(ξ,η)为物光,ur(ξ,η)为参考光,物光与参考光干涉平面为(ξ,η),CCD 所在平面为(x,y),则毛玻璃后表面光场复振幅分布可以表示为
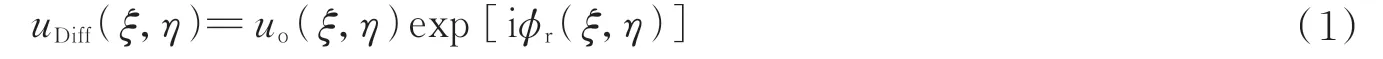
在BS2 处物光与参考光干涉,其复振幅分布可表示为
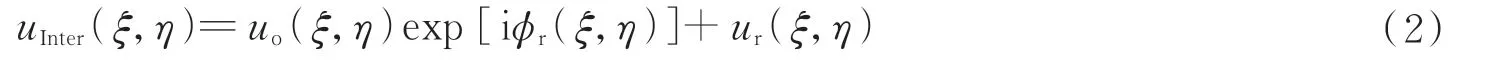
根据衍射理论,CCD 平面上散斑场的复振幅分布由散斑场与镜头的点扩展函数(Point Spread Function,PSF)的卷积得到,即
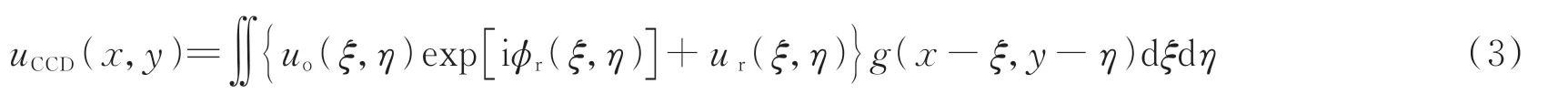
式中,g(x,y)表示CCD 相机上安装的镜头的PSF。由于要远程记录全息图,为了降低散斑噪声,可以通过旋转毛玻璃对散斑场强度进行时间平均。假设散射介质产生了一个平稳的、遍历的场,并且是δ相关的,可以用时间平均值代替集合平均值,即

因为只对物光进行了散斑平均操作,根据δ函数性质可知在这种近似下CCD 平面的时间平均场强可表示为
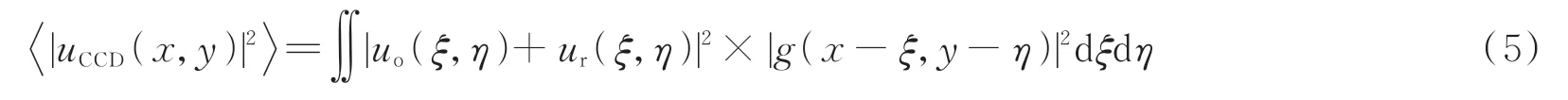
对于无透镜傅里叶变换全息图,利用光强分布的傅里叶变换重建图像,即
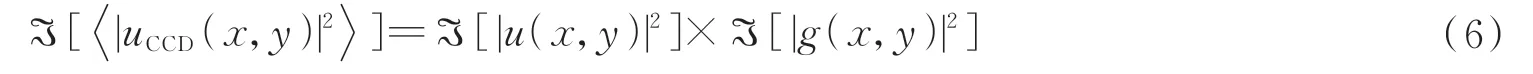
式中,ℑ 表示傅里叶变换,式(6)等号右边第一项给出了由传统无透镜傅里叶变换全息图重构的中央亮斑和共轭的重建图像,第二项为透镜的传递函数。
1.2 探究毛玻璃旋转速度及CCD 曝光时间对成像质量的影响
由分析可知,通过旋转毛玻璃可以对散斑场强度进行时间平均,增强干涉散斑图像的条纹对比度,但旋转速度过快会导致重建图像出现部分信息丢失的情况,所以毛玻璃的旋转速度存在最佳值。CCD 相机的曝光时间同样也会影响重建图像的质量,故需通过实验探究二者对重建图像质量的影响。
实验中,将毛玻璃固定在由电机驱动的中空旋转平台上,置于光路中,由驱动器调节毛玻璃旋转速度。探究不同曝光时间下,毛玻璃旋转速度对重建图像PSNR 的影响。并以同样的方法探究在不同的旋转速度下,曝光时间对重建图像PSNR 的影响,实验结果如图2所示。
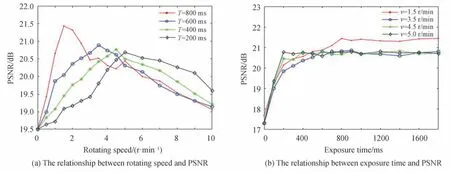
图2 毛玻璃旋转速度及CCD 曝光时间对成像质量的影响Fig.2 Influence of the rotation speed of ground glass and the exposure time of CCD on the image quality
如图2(a)所示,毛玻璃旋转速度对重建图像PSNR 的影响呈现出先升高后下降的趋势,且在不同的曝光时间下,毛玻璃最佳旋转速度有所不同。当曝光时间为800 ms,旋转速度为1.5 r/min 时,取得四组数据中最高PSNR,为21.44 dB。由图2(b)可知,CCD 相机的曝光时间对重建图像PSNR 的影响呈现出先上升后趋于平稳的趋势,且在不同的转速下,重建图像PSNR 趋于稳定所需的曝光时间也不同,旋转速度越快,所需的曝光时间越短,但重建图像PSNR 略有下降。在实际应用中,可根据不同的场景需求选择合适的曝光时间。
1.3 实验结果
实验中所用激光器(Thorlabs-HNL050L)中心波长为632.8 nm,凸透镜焦距为300 mm,CCD 相机(HamamatSU-C13440)分辨率为2 048×2 048 像素,CCD 上安装的镜头(Computar)焦距f=25 mm,光圈为F1.4,散射介质采用220 粒度的毛玻璃,将毛玻璃固定在中空旋转平台上,保证毛玻璃与CCD 相机接收平面垂直,利用驱动器使毛玻璃以1.5 r/min 的速度旋转,同时将CCD 相机的曝光时间设置为800 ms。CCD 相机上安装的镜头需准确聚焦在BS2 表面,保持大光圈以接收到更多光,在CCD 相机获取到干涉散斑图像之后,只需做简单的傅里叶变换即可恢复出物体信息。采用细节丰富的硬币、玩偶进行实验,结果如图3所示。
图3(a)、(d)分别为CCD 记录的玩偶和硬币的部分全息图,图3(b)、(e)为毛玻璃不旋转时的重建图像,由于没有执行散斑平均操作,重建图像噪声大,对比度低,几乎无法辨认出物体。图3(c)、(f)为毛玻璃旋转时的重建图像,此时利用时间平均值代替集合平均值,散斑场得到平均,重建图像对比度和分辨率得到有效提高。通过实验可知,散斑平均操作可有效提高重建图像质量,且适用于多种场景。

图3 不同物体的重建图像Fig.3 Reconstructed images of different objects
2 透过双散射介质成像
由于实际成像问题中很难遇到旋转或带有微小位移的散射介质,在系统中引入一个实际场景中常见的静置散射介质,实现透过两个散射介质成像,从而增强该方法的实用性。
2.1 基本原理
在SLM 上加载随机散斑图像充当第一个散射介质,利用MATLAB 生成0~255 灰度的随机散斑图像,在加载到SLM 上之后每一个灰度都映射为0~2π 之间的不同相位,以此模拟由散射介质引起的随机相位变化,实验光路如图4所示。
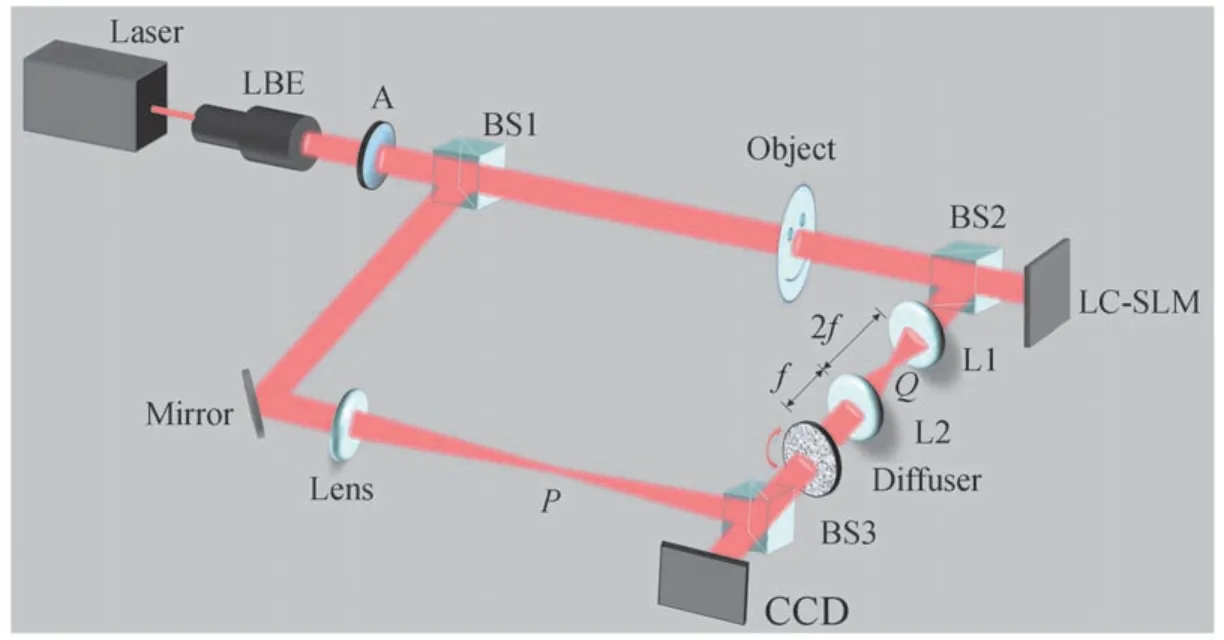
图4 双散射介质实验光路Fig.4 Experimental light path diagram of double scattering medium
设uo(ξ,η)为物光,ur(ξ,η)为参考光,ϕSLM(ξ,η)为SLM 引入的随机相位,则在SLM 表面的复振幅分布可以表示为
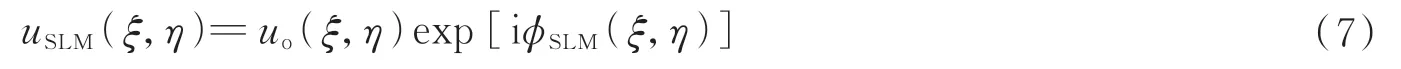
如果SLM 的像素宽度足够大,那么在经过SLM 之后的波长变化相对缓慢,SLM 与透镜L1 之间的距离为f,在Q点处放置一个小孔以选通SLM 的0 级衍射光。经过4-f系统成像后,SLM 表面的物光场信息准确聚焦在旋转毛玻璃前表面上,设4-f系统的PSF 为g(ξ,η)且与δ相关,毛玻璃后表面上光场复振幅可表示为经化简后可得出与式(1)相同的形式,即
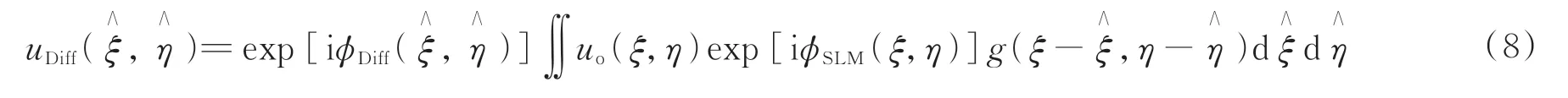
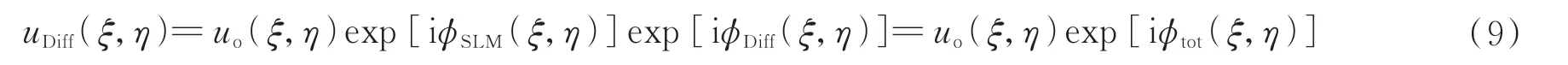
后续推导过程与透过单个散射介质成像理论部分相同,这里不再赘述。因此,对获得的干涉散斑图像进行傅里叶变换即可重建出物体信息。
2.2 实验结果
实验中采用美国空军USAF 1951 分辨率板作为物体,重建结果如图5所示,图5(a)、(b)分别为SLM 上加载的随机散斑图像和CCD 相机记录的全息图的局部,图5(c)为执行散斑平均操作时的重建图像,实验中通过旋转毛玻璃和增加CCD 的曝光时间降低散斑噪声,使得数字全息再现时中央亮斑增大,降低了重建图像对比度,对重建图像进行巴特沃斯高通滤波消除中央亮斑,如图5(d)所示,重建图像对比度和清晰度得到有效提高。值得一提的是,重建图像中圆形亮纹是由于全息再现时,参考光经过傅里叶变换发生自相关导致,亮纹由中央向周围环形扩散,无法通过低通滤波消除。实验验证了散斑平均操作能够有效恢复被两个散射介质遮挡的物体的信息,静置散射介质的引入使得该方法更适用于实际场景。

图5 双散射介质重建图像Fig.5 Reconstruction image of double scattering medium
3 结论
本文基于统计平均方法和无透镜傅里叶变换数字全息技术实现了透过单个散射介质和双散射介质的清晰成像,并研究了成像系统中对重建图像PSNR 有重要影响的两个参数——散射介质旋转速度和CCD 曝光时间。实验表明在不同的曝光时间下,获得重建图像最高PSNR 的毛玻璃旋转速度有所不同,旋转速度越快,达到最高PSNR 所需的曝光时间越短。对获得重建图像可选取合适的截止频率,进行巴特沃斯高通滤波消除中央亮斑以提升其对比度及清晰度。所设计的系统结构简单、紧凑且成本低,不需要连续扫描和数值迭代计算即可重建图像,实验结果很好地验证了该方法的可行性,再加之简单的重建方法,非常有希望应用于实际复杂场景的实时成像。

