基于改进偏振双向反射分布函数的海面场景红外偏振成像仿真

谭畅，王世勇，高思莉，陈丽，陈玮琳，裘莉娅

（1 中国科学院上海技术物理研究所，上海 200083）

（2 中国科学院红外探测与成像技术重点实验室，上海 200083）

（3 中国科学院大学，北京 100049）

0 引言

海面舰船是海上搜救和海岸线监测的重点关注对象，目前海面监测主要采用红外探测［1］，但当海面目标温度与海水温度相近时，基于辐射强度的传统红外探测存在较大的局限性。同时，海面这一特定探测场景对太阳和天空光的强烈反射所产生的太阳耀光进入成像系统，也可能导致目标丢失。红外偏振探测作为一种新型探测技术，可以获得偏振多维信息，在探测目标辐射强度的同时，还能够反映其偏振信息，对太阳耀光也有很好的抑制作用，有针对性地解决了海洋场景下传统红外目标探测的两大难题。针对不同场景对舰船目标进行红外偏振仿真，产生大量数据对红外偏振目标探测与识别系统进行训练，不但有助于提升性能，且大大降低了训练成本。

红外偏振仿真技术作为提升偏振探测技术的重要辅助手段，可为红外偏振探测器的设计提供理论依据与参考。国外对于红外偏振仿真技术的研究开始较早，已有比较成熟的具备偏振仿真能力的仿真平台，如美国罗切斯特理工学院数字成像和遥感试验室开发的仅向美国政府机构和合同商发布的DIRSIG，已具备偏振仿真的功能。GARTLEY M G［2］介绍了DIRSIG 的软件框架与仿真流程，MEYERS J 等［3］阐述了辐射传输矩阵的修正方法，使其具备偏振成像仿真的功能。BOGER J K［4］建立了长波红外偏振探测器的全链路仿真模型，BJÖRKERT S 等［5］改进了传统偏振双向反射分布函数（polarized Bidirectional Reflectivity Distribution Function，pBRDF），使其更适用于场景仿真。

国内对目标的偏振特性研究起步较晚，目前还没有成熟的具备偏振仿真功能的商用仿真软件推出，马帅等［6］考虑了目标的自发辐射，建立了双参数的pBRDF 数学模型；柳祎等［7］基于微面元双向反射分布函数模型，构建出含有遮蔽函数的粗糙表面红外辐射偏振度的斯托克斯解析模型；汪杰君等［8］综合考虑镜面散射和漫散射，构建了一种改进的偏振双向反射分布函数模型，并利用该模型对材料的复折射率进行了反演。

对于成像仿真来说，最精确的方法是光线追迹法，利用全局光照的思想，模拟出所有光线与表面的全部能量交互，但是对于偏振成像仿真来说，在原本海量计算的基础上，又多了偏振态的传输过程，MOBLEY C D［9］曾在2.5 GHz 的计算机上生成105 个表面，追踪大约36×106 条光线，所需时间超过8 h，这一时间成本对于大部分工程来说都是灾难性的。本文结合Pierson-Moscowitz（P-M）海浪谱与Cox-Munk 模型建立了具有粗糙度的海面三维几何模型，设计了适用于红外偏振成像仿真的三维数据存储结构，改进传统Priest Germer（P-G）双向反射分布函数，仿真模型实时性得到改善。

1 三维几何模型建立

1.1 基于海浪谱的海面三维模型建立

选择基于海浪谱的方式构建海面的三维模型，海浪谱反映海面海浪在传播方向和波长上波能的统计分布，即海面高度起伏相关函数的傅立叶变换，是海面的功率密度谱。可通过快速傅里叶逆变换（Inverse Fast Fourier Transform，IFFT）将海浪谱模型转换为高度场，进而建立海面的几何模型［10］。

选择以风速作为唯一参量的PM 谱生成海面三维模型，其公式为

式中，k为海浪波数，δ为大尺度广义平衡参数，取8.1×10-3，U19.5为海面上方19.5 m 处的风速，g为重力加速度。

已知PM 海浪谱随方向变化的分布函数为

则二维PM 谱可表示为

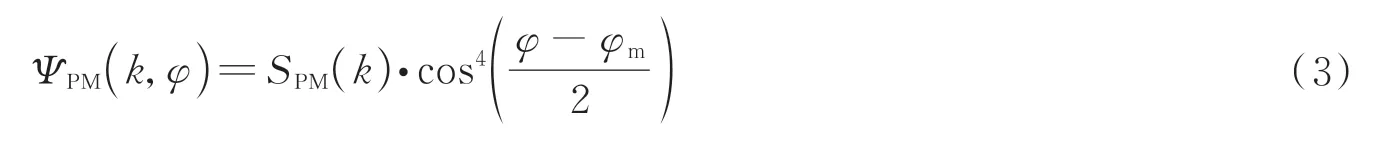
式中，φm为海浪传播方向，φ为风向角。由此可利用二维PM 海浪谱生成海面高度场，首先设定欲仿真的海面尺寸Lx、Ly，并确定空间快速傅里叶变换（Fast Fourier Transform，FFT）网格数目M和N，从而得到波数K=（kx，ky），kx=2πm/Lx，ky=2πm/Ly，m和n的取值为区间［-M/2，M/2］和［-N/2，N/2］内的整数，再根据网格点的坐标（x，y）与波数计算得到对应的频率ω。计算出海面上每一点Ph（K）值，并得到用于生成海浪高度场的振幅(K)，根据其共轭性，通过IFFT 计算出海面某一点的瞬时波高h（x，y），即

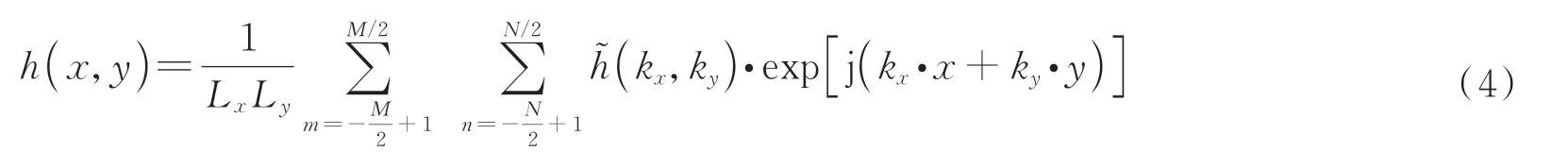
由此可以根据不同风速绘制出海面不同时刻的瞬时波形，但对于偏振仿真来说，还需要获得微面元尺度的海面斜率方差（σ2），即海面粗糙度，可用Cox-Munk 模型来计算，即

式中，W12.5为海面上方12.5 m 处的风速。

由此获得了用于红外偏振仿真的全部海面参数，创建如图1所示的海面三维模型。

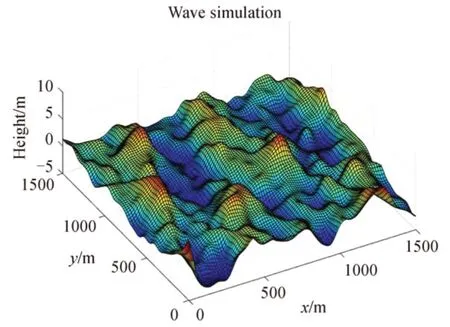
图1 由P-M 海浪谱生成的海面三维模型Fig.1 Sea surface 3D model generated from P-M wave spectrum

1.2 舰船三维模型构建

选择3D MAX 作为构建目标三维几何模型的建模工具，舰船3D 模型如图2所示，用三角面元作为基础面元构建模型表面，选择便于编辑的ASE（ASCII Scene Export）文件格式将模型数据导出［11］，ASE 文件中的面元和顶点数据以最初建立模型时的子模块为单位进行存储，为保证模型的精确性一般会建立较多的子模块，导致仿真时访问顶面和面元数据变得复杂，文件中材质数据一般针对可见光成像，对于红外偏振仿真来说，不需要模型的光照与颜色数据，但对于不同的材质模块，需要添加其复折射率与粗糙度等材质属性，因此，将原始ASE 文件中顶点和面元按照面元所处舰船部位和材质的不同重新划分模块，并对每个模块中顶点和面元重新组合编号，ASE 文件的具体数据结构如表1所示。

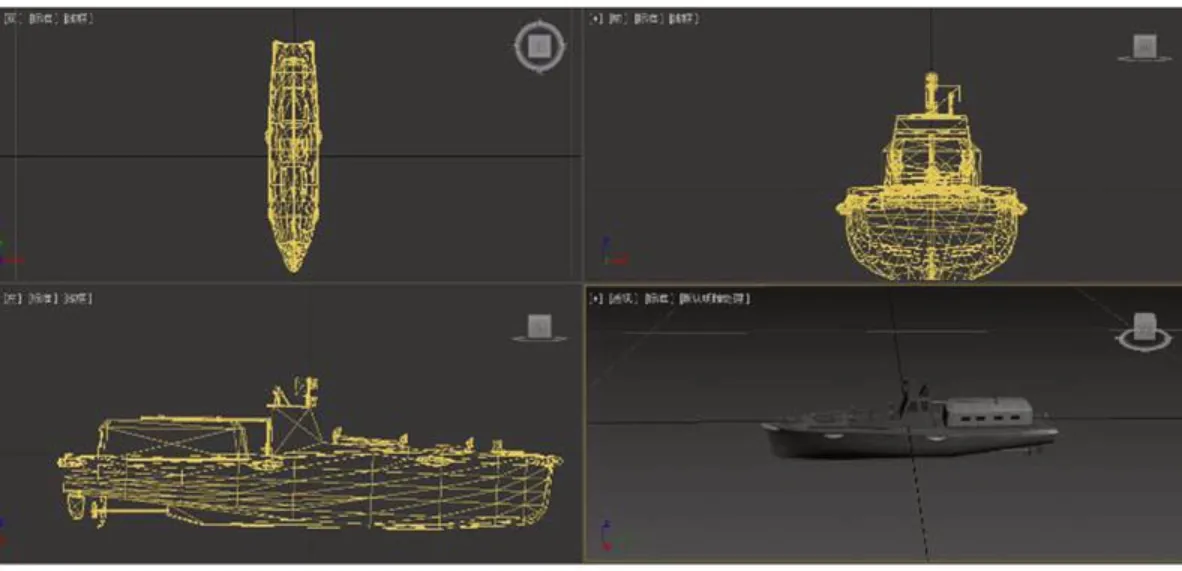
图2 舰船三维几何模型Fig.2 Three dimensional geometric model of ship

表1 模型文件数据结构Table 1 Data structure of model file

2 红外偏振辐射模型

2.1 辐射能量模型建立

到达探测器孔径的总有效辐射可用辐射控制方程表示［12］，根据实际仿真需求得到简化后的公式为

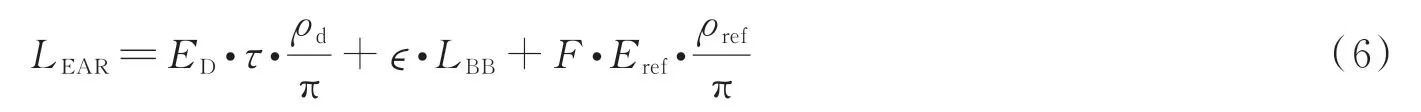
式中，ED为太阳直接辐照度，τ为大气透过率，ϵ为目标发射率，LBB为目标自发辐射，F是取值为0 到1 的缩放因子，Eref为太阳散射辐射辐照度，ρd与ρref为表面对太阳直接辐射与散射辐射的反射率。该控制方程列出了从目标、背景和大气路径向传感器反射或发射的有效辐射，辐射传输过程如图3所示，通过描述其辐射量与偏振态的传输过程，最后得到目标红外偏振成像仿真的理论模型。

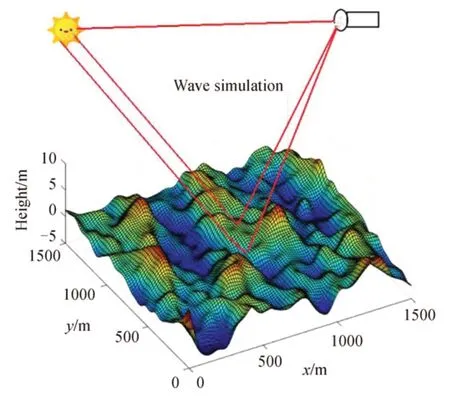
图3 辐射传输示意图Fig.3 Schematic diagram of radiation transmission

舰船与海面接收到的外部辐射主要是太阳的直接辐射与散射辐射［13］，可将这部分入射辐射视作非偏振光，经过介质表面的反射，才会产生偏振效应。太阳直接辐照度计算公式为

式中，E0为太阳常数，取1 353 W/m2，ρt为大气透明度，α为大气质量，θT为太阳光的入射角。

太阳散射辐射辐照度计算公式为

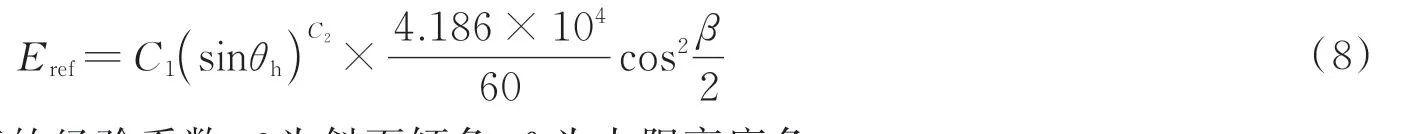
式中，C1和C2是取决于大气透明度的经验系数，β为斜面倾角，θh为太阳高度角。

自发辐射的能量部分由普朗克定律求出，辐射的空间分布率与偏振状态将在2.2 节中讨论。

式中，h为普朗克常数，c为光速，λ为探测波长，k为玻尔兹曼常数，T为目标的表面温度。

2.2 偏振传输模型建立

在偏振光的传输中发生的透射反射等过程，都可以表述为穆勒矩阵与光波Stokes 矢量的作用，假设入射光Stokes 矢量为Sin，出射光的Stokes 矢量为Sout，则有

用pBRDF 模型表征反射过程中的能量传输过程，分析几种常见的pBRDF 模型，他们有相同的一般形式，即偏振的镜面反射分量fpBRDF与非偏振的漫反射分量fvol，而镜面反射部分也都是由菲涅尔反射穆勒矩阵M、材质表面的统计分布P（θN）和阴影与遮挡函数SO（θ，β，τ，Ω）三部分组成，非偏振部分则由体散射项ρd与漫反射项ρv组成，其具体表达式为

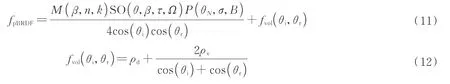
式中，θi，θr分别为入射方向和出射方向与宏观表面法线方向的夹角。

PG 模型的一大优势是参数简单，除入射角与出射角外输入参数只需要材料的复折射率与粗糙度（即材质表面斜率方差σ2）。对于菲涅尔反射过程，主要工作是Mueller 矩阵各参数的计算，不考虑圆偏振光的情况下，S3分量为0，只需求解Mueller 矩阵的9 个分量即可，其具体计算公式在文献［14］中有详细讨论。统计分布函数和阴影遮挡函数的数学公式为

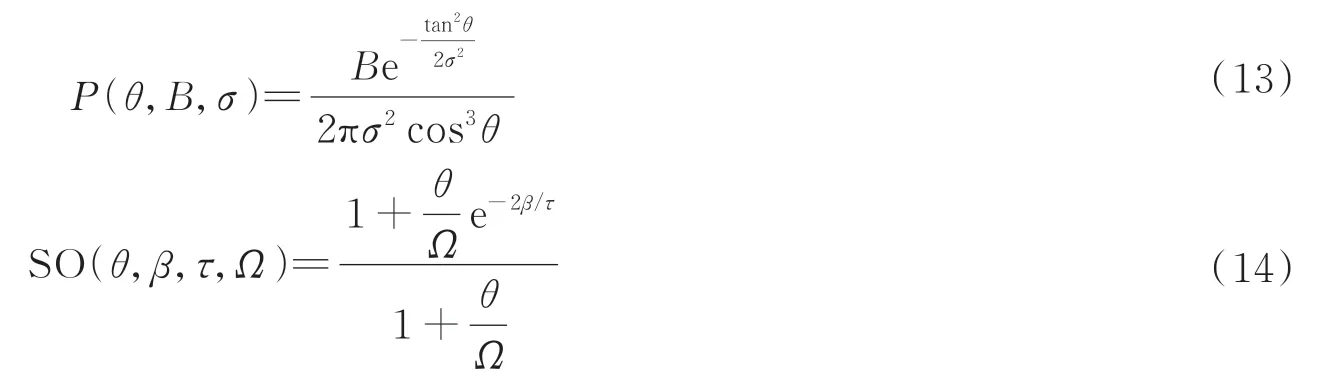
式中，B为偏置参数，σ为粗糙度参数，τ和Ω为描述阴影与遮蔽效果的参数。

为使模型更适应于计算机成像仿真，结合计算机图形学实时渲染中应用最广泛的Cook-Torrance BRDF 模型，对PG 模型的统计分布函数和阴影遮挡函数做出改进。

模型的每一个三角面元都看作由许多不可再逐像素分析的微平面组成，而粗糙度则是反应微平面法线取向的参数，即平面越粗糙，微平面法向排列越混乱，统计分布函数计算的是某一方向向量与面元平均取向方向一致的概率。而阴影遮挡函数则是为了计算微平面之间相互遮蔽的概率。可以将入射方向与观测方向间的中间向量近似看作这些微面元的平均取向，则式（13）、（14）可简化为

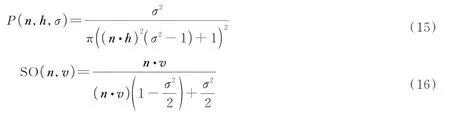
式中，h为微平面平均取向的中间向量，由入射方向向量与观测方向向量求得，n为面元的法线向量，v为探测方向，各向量示意如图4所示。函数的输入参数仍仅为入射方向、出射方向与材质粗糙度，避免了复杂的指数运算，实验表明每一面元对其阴影遮挡函数与统计分布函数改进后，可减少2 ms 的运行时间，对于采用的舰船模型，共1 974 个三角面元，每一场景可减少耗时4 s，对于更大规模的场景，模型将会展现出更大的优越性。

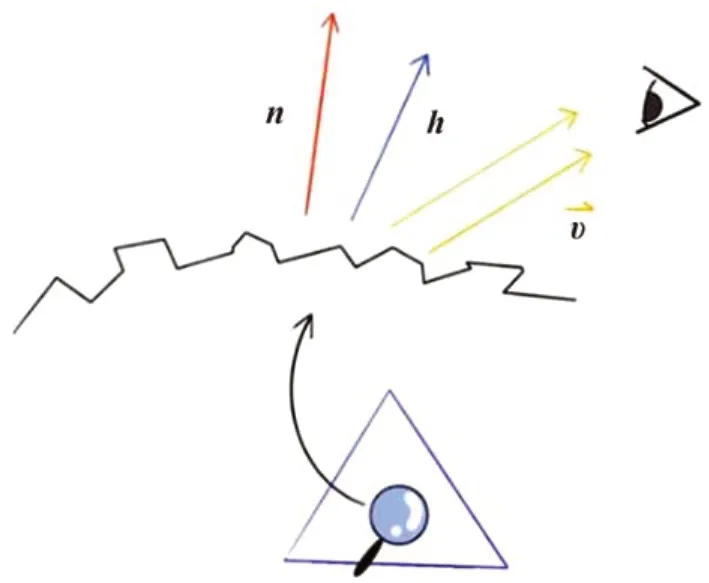
图4 中间向量示意图Fig.4 Intermediate vector diagram

被测平面的方向半球反射率ρDHR可表示为

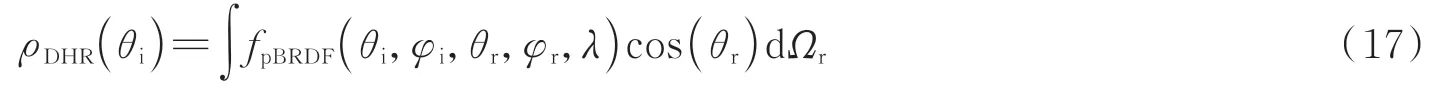
式中，dΩr=sinθrdθrdφr，由此完成了用菲涅尔反射Muller 矩阵及微面元理论改进的PG 模型来表示入射辐射到反射辐射的传输关系。

在建立偏振发射率模型时，假设材料在光谱的红外区域透射率为0，得到该面元的反射率后，根据基尔霍夫定律，可由半球反射率来求解发射率［15］，即

简化后，对应探测角θ，入射到探测器的总红外偏振辐射为

2.3 灰度映射

得到各分量的辐亮度后，计算出探测器接收到的辐照度为

式中，Lsum为面元总的红外辐射亮度，R为探测器与面元之间的距离，Ad为探测器光敏元的有效面积，f为光学系统的焦距。可得到输出的电压信号为

式中，D为光学系统的口径，ρs为探测器的光学透过率，Rv为探测器的响应率，τa为由MODTRAN 计算得到的大气透过率。

经过光电转换后的响应电压最后转换为相应灰度等级中的灰度值，即

式中，B为模数转换对应的灰度量化等级，Vlb为电压的量化精度，VH为电路设置的输出上限电压，VL为电路中输出下限电压。

3 仿真结果

依据文献［2］的实测数据，对舰船与海面的表面材质赋值，见表2。表中σ为材质粗糙度，B为偏置参数，n和k代表了材质的复折射率，ρd与ρv为非偏振的体散射项与漫散射项。

表2 舰船与海面材质属性Table 2 Material properties of ship and sea surface

依据建立的理论模型，对于不同的探测角度，分别对舰船与海面的发射率与反射率的3 个分量进行计算，得到结果见表3～4。由于舰船与海面偏振方向半球反射率的S2分量都接近于0，在此不做计算。

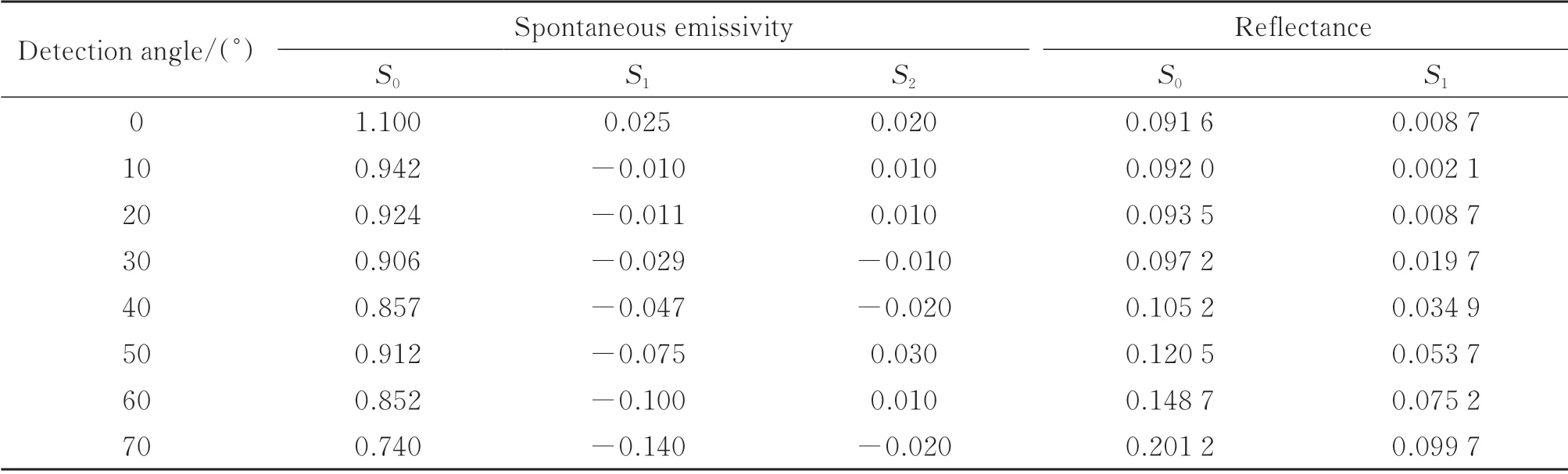
表3 海面定向半球偏振自发辐射率和偏振反射率Table 3 Hemispherical spatially polarized spontaneous emissivity and reflectance of sea surface

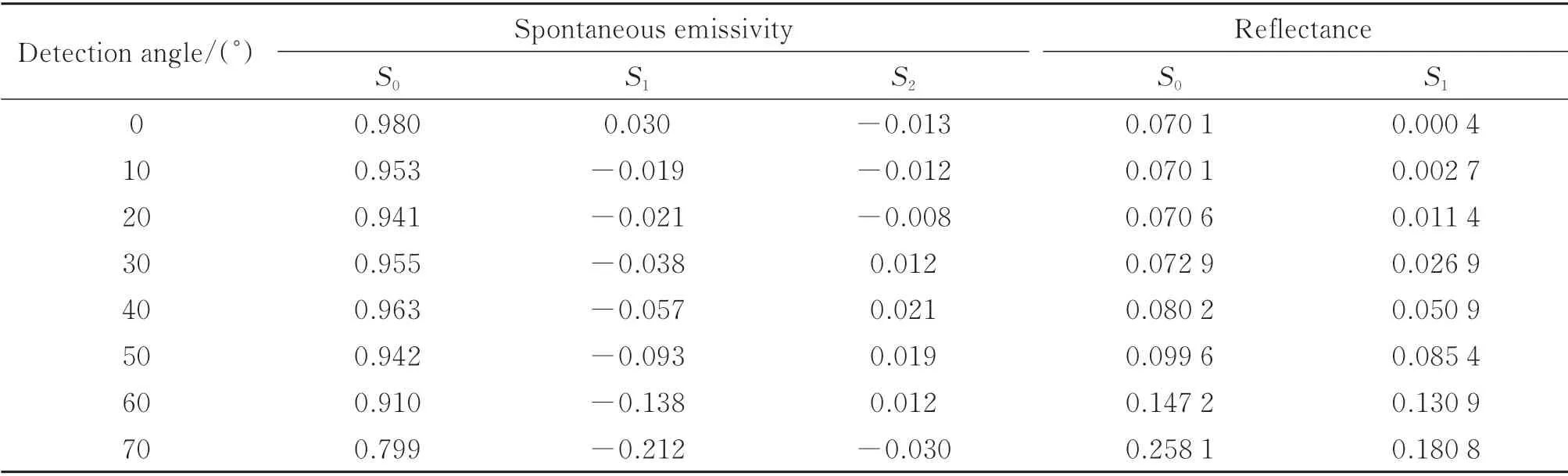
表4 舰船定向半球偏振自发辐射率和偏振反射率Table 4 Hemispherical spatially polarized spontaneous emissivity and reflectance of ship

图5展示了基于改进仿真模型生成的仿真图像，与相近条件下采集的真实图像，具体仿真参数见表5。其中方位角与探测方向角均为与当地正北方向的夹角。

图5 舰船与海面的仿真图像与实测图像Fig.5 Simulated and measured images of ship and sea surface

表5 仿真参数设置Table 5 Simulation parameter setting

对比图6仿真与实测偏振度图像的灰度分布，可以看出二者有较强的相似度，但由于实拍图像中还有落叶、围墙、钢管等因素存在，部分区域存在一定的差异。同时可以看出，对于反射主导的短波红外探测来说，舰船与海面的S2分量都趋近于0，与提出的理论模型相符，在实测图像与仿真图像上也有所体现。

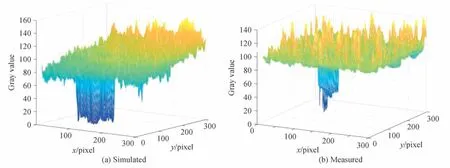
图6 仿真与实测偏振度图像的灰度分布Fig.6 Gray distribution of simulated and measured polarization images

同时，为证明提出模型在仿真实时性方面的优势，对不同风速下不同面元数的海面与舰船目标分别采用传统PG 模型与本文提出的改进模型，在6 核心2.6 GHz，GTX 1660Ti 的计算机上进行成像仿真，耗时结果如表6。

表6 仿真节约耗时对比Table 6 Comparison of simulation time saving

因为提出模型的改进主要针对每一面元的阴影遮挡函数与统计分布函数，因此与目标自身的材质属性如粗糙度关系不大，主要取决于目标的面元数，从结果也可以看出，模型越复杂，面元数越多，改进模型相较于传统模型仿真节约的时间越多，优势越明显。

4 结论

本文根据海浪谱生成了海面的三维几何模型，针对红外偏振仿真的所需参数，设计了合理的数据存储结构。对辐射控制方程进行了简化，提出一种更适用于计算机实时渲染的偏振双向反射分布函数模型，平衡了仿真的真实性与实时性要求，同时建立了舰船与海面的半球空间发射率模型，综合考虑了海面与舰船的反射效应与自发辐射，基于探测器的焦距、孔径、响应率等参数建立了初步的探测器模型。采集了相似条件下真实水面上的舰船图像与仿真图像进行对比，二者偏振度图像的灰度分布较为相似。分别对海面目标成像仿真的耗时结果表明，该仿真模型相较于传统模型，在保证模型正确性的前提下，提升了成像仿真的速度。