基于模糊控制的智能验电接地机器人机械臂运动控制研究

刘益军，李正强，赖建防，吕伟宏

（1.广东电网有限责任公司 佛山供电局，佛山 528000；2.宁波天弘电力器具有限公司，宁波 315700）

验电接地是电力现场作业防止人员触电的必要安全措施。传统架空线路验电接地作业方式存在较高风险：一是需要作业人员登高并人工验电及装设接地线，存在高空坠落和触电风险；二是工器具设备沉重，接地线易缠绕身体，单纯依靠人力执行耗时、耗力，效率低下[1-3]。如今使用机器人代替部分人工作业，降低人员风险成为解决方案之一，但为使验电接地机器人准确完成验电、接地工作，即对机械臂运动进行精确控制，需对机器人控制算法进行研究。

现有的机械臂运动可分为基于模型与不基于模型的方法。基于模型的方法有反演控制、自适应控制、滑模控制等，受限于系统数学建模的建立，多应用于动力学特性简单的系统[4-8]；不基于模型的控制方法有PID 控制、模糊控制等，解决控制中的误差和干扰问题，但参数的选择以经验为主[9-11]。

智能验电机器人机械手具有两个关节，是一个多输入、高度非线性、强耦合的系统，存在负载质量、连杆质心位置、动静摩擦力等不确定参数，使传统控制方法效率降低，难以得到准确数学模型[12-14]。综上所述，综合反演控制、自适应控制、模糊控制的特点，提出了基于自适应模糊反演控制算法，实现对智能验电机器人机械手运动轨迹精确控制。

1 机械臂自适应模糊反演控制模型建立

为使智能验电机器人机械臂运动满足预设轨迹，即通过控制各关节输出力矩，使机械臂位置、速度等变量满足运动要求，需对机械手闭环运动控制算法进行研究，本文建立的闭环控制系统如图1所示。

图1 智能验电机器人机械臂闭环运动控制系统框图Fig.1 Block diagram of closed-loop motion control system of robot arm of intelligent electro-detector robot

结合模糊理论与自适应控制，设计适用于智能验电机器人机械臂自适应模糊控制器，通过实时修正控制系统参数，使控制器适应变换的动态载荷，避免人的经验获得模糊控制规则的主观性。智能验电机器人两自由度机械臂机构简图如图2所示。

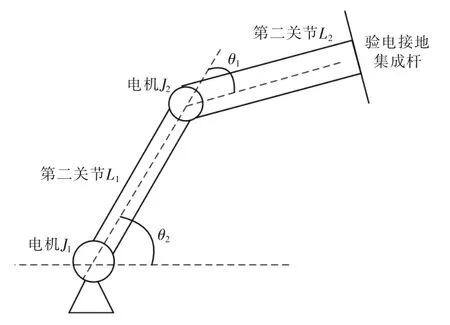
图2 智能验电接地机器人机械臂机构示意图Fig.2 Schematic diagram of mechanical arm mechanism of intelligent electric grounding robot

对机械臂进行动力学分析，动态方程如下：

机械臂转动惯量与向心力和科里奥利力关系如下：

1.1 机械臂反演控制器设计

为便于反演控制器设计，设x1=θ，x2=，式（1）可表示为[17]

式中：d 为外界干扰项，反演控制器的控制目标为关节角度y，定义实际运动轨迹与理论轨迹角度误差为

角速度误差为

式中：λ1为机械臂第一关节控制系数；为估计量一

阶导数。

针对机械手第一关节，取李亚普洛夫函数为

当e2=0 时，第一关节运动稳定。对于机械手第二关节，角速度误差导数可表示为

对于机械手整体，可取控制力矩为

式中：λ2为机械臂第二关节控制系数，φ 为角度误差。

机械臂第二关节李亚普洛夫函数为

对式（10）求导，结合机械手整体控制律得：

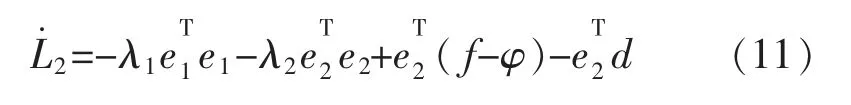
1.2 机械臂自适应模糊控制器设计

本文模糊系统部分由单值模糊化、中心平均反模糊化和乘积推理机模型构成。机械臂第一关节、第二关节转动角度θ1，θ2和角速度为模糊系统输入，定义模糊集：负（N），零（Z），正（P）。机械臂第一、二关节模糊系统为[18-19]

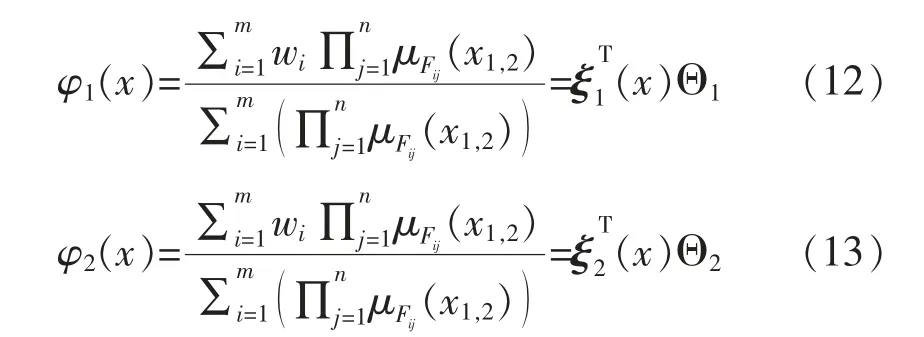
式中：w 为系统输出；μF为高斯分布函数；ξ1T，ξ2T为模糊矢量。Θ1= [w1，w2，…，wm]T，Θ2= [w1，w2，…，wn]T，为系统输出矢量。

2 仿真试验

仿真试验基于MATLA 工具箱Simulink 进行，通过对机械臂双关节控制进行自适应反演模糊控制算法分析。为便于仿真，对机械臂进行坐标设定[20]，结构如图3所示。

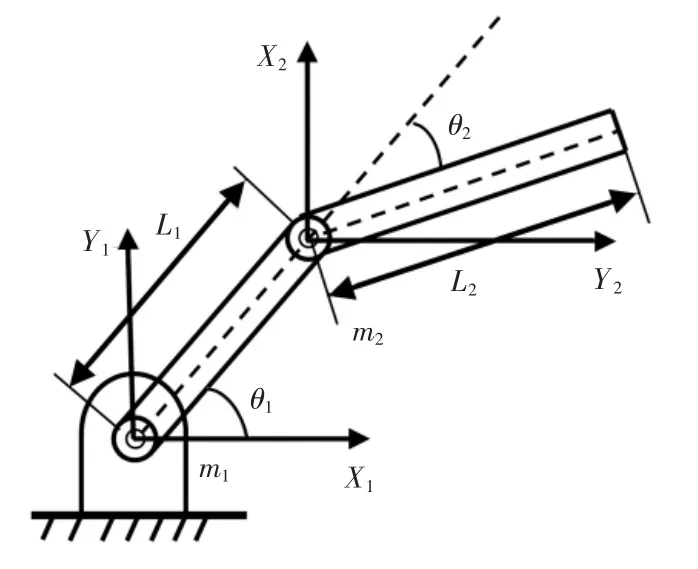
图3 双关节机械臂Fig.3 Double-joint robotic arm

图3中L1，L2为两连杆长度；m1，m2为两连杆重量；θ1，θ2为连杆转动角度。简化后机械臂参数如表1所示。

表1 机械臂参数Tab.1 Manipulator parameter

根据连杆运动方式可将机械臂关节角度表示为

设机械臂初始状态为x（0）＝[1，0 ]T，关节期望轨迹为y=sin（2πt），模糊系统中采用高斯函数作为隶属度函数：

取函数均值ci分别为-1.25，0 和1.25；函数偏移量σ 为0.5。求得隶属度函数如图4所示。

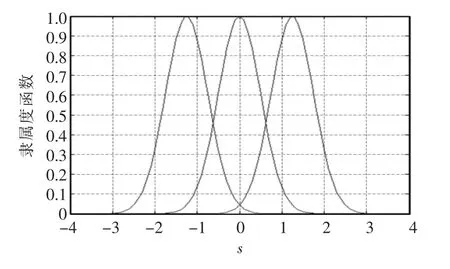
图4 模糊隶属度函数Fig.4 Fuzzy membership function

设自适应模糊反演算法中第一、二关节控制系数分别为：λ1＝6，λ2＝10。因实际控制中机械臂制造及安装精度等外部因素影响，为减小控制算法仿真精度与实际精度误差，设随机干扰误差d=［0.2sint，0.2cost］，误差采样时间周期为0.01 s。则关节一、二位置轨迹跟踪及跟踪误差仿真如图5和图6所示，其中跟踪误差为仿真轨迹与理论轨迹之差。

图5 关节一定位分析Fig.5 Positioning analysis of joint 1

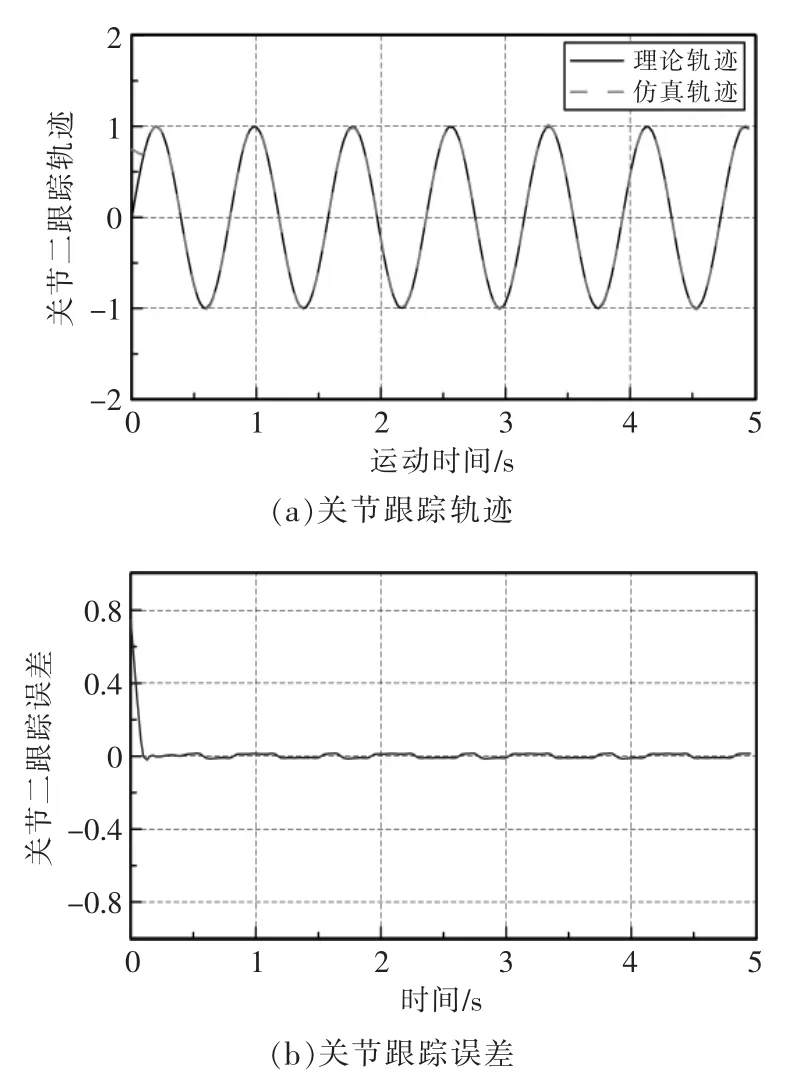
图6 关节二定位分析Fig.6 Positioning analysis of joint 2

由图5和图6可知，自适应模糊反演算法对机械臂双关节控制均具有较高跟踪精度，其跟踪误差均小于0.80 rad，满足工程需求。因存在响应时间，所以关节初始运动阶段，跟踪误差较大，当运动达到稳态时，关节仿真跟踪轨迹与理论轨迹误差较小。稳态时关节一最大跟踪误差为0.0075 rad，响应时间为0.12 s，关节二最大跟踪误差为0.012 rad，响应时间为0.09 s。

综上所述，自适应模糊反演控制算法对验电接地机器人双关节机械臂运动控制具有良好的适用性，解决了机械臂运动过程中的非线性及不确定性问题，较传统的模糊控制算法，响应时间较短，跟踪定位精度有显著提高。

3 结语

本文提出自适应模糊反演算法应用于智能验电机器人机械臂控制，解决了系统中参数不确定、高非线性、强耦合等问题。在自适应模糊反演算法下机械臂双关节响应时间分别为0.12 s，0.09 s，稳态时最大跟踪误差分别为0.0075 rad，0.012 rad。自适应模糊反演算法对机械臂双关节控制均具有较高跟踪精度，其跟踪误差均小于0.80 rad，满足跟踪精度需求。

针对机器人机械臂运动控制难度高、技术复杂的难题，结合反演控制、自适应模糊控制理论，提出了自适应模糊反演控制算法，实现了智能验电机器人机械臂运动轨迹闭环控制。完成了机械臂反演控制器、自适应模糊控制器设计，通过仿真实验验证了跟踪控制的准确性和适用性，对机器人结构设计、工程应用具有重要指导意义。