基于生成对抗网络的强化学习算法的研究

俞君杰

(江苏电力信息技术有限公司， 江苏， 南京 210013)

0 引言

生成对抗网络是最近提出的一类生成模型，其训练了生成器以优化区分器同时学习的成本函数[1]。尽管学习成本函数的概念在生成建模领域相对较新，但长期以来，人们仍然采用强化学习算法模型，导致存在学习效率低下，收敛速度慢等种种缺陷[2-3]。

因此，许多学者不断研究其改进和替换方法。文献[4]公开了ASE学习算法，通过改进样本的采样工序来提高目标函数的精确度。该算法通过人工智能的方式提高了数据应用和训练能力，但数据学习过程和应用能力方法没有提及，无法获取数据训练或者计算的过程，工作效率滞后，也无法解决相关技术问题。文献[5]应用一种通过小计算获取大效果的Q学习算法，应用过程中，计算量比较小，该算法能够输出较佳的数据最优解，对于解决复杂数据问题具有突出的技术效果，能够通过随机的方式实现数据的动态变化，大大提高了数据应用能力。该算法训练样本的过程复杂，且对计算机系统性能要求过高，具有一定的局限性。本文借助生成对抗网络的思想，给出用生成对抗网络实现强化学习算法，下面将具体阐述该算法的结构框架和相关理论内容理论背景、基本思路、算法实现和实验分析。

1 相关理论

1.1 强化学习理论

在具体学习和应用中，该研究构建的马尔科夫决策过程(MDP)能够提高数学建模能力，尤其是在强化学习中，MDP应用在完全可观测的技术环境中具有一定现实意义，观测到的状态内容完整地决定了决策需要的特征，几乎所有的强化学习问题都可以转化为MDP。一个MDP过程受几个重要参数所影响，该重要数据参数因素中存在有限的数据信息状态集s，有限的数据信息动作集A，还能够实现使数据信息进行转移的状态转移概率P，实现数据信息回馈的回报函数R，将数据信息进行折算的折扣因子γ。在MDP从状态到动作的映射过程为

Pss′=P(st+1=s′|st=s,at=a)

(1)

π(a|s)=P(at=a|st=s)

(2)

其中，t表示一个时间间隔，a表示目标函数。根据MDP回报函数R能够得出累计回报为

(3)

其中，G代表累加回报值，k代表回报函数R的自变量。由式(3)得出状态处的期望回报值V为

(4)

由式(4)得出动作处的期望回报值Q为

(5)

综上式得出最有函数解的公式为

(6)

1.2 生成对抗网络理论

在具体应用过程中，将生成对抗网络作为生成建模的一种方法，通过生成模型G和判别模型D两种不同的方式实现数据信息评估与分析。实现数据信息生成对抗网络的判别模型能够将数据信息通过输入分类数据信息，进而将数据信息通过生成模型的方式进行输出，进一步将能够实现的基础数据样本信息通过信息p(x)的形式实现输出。为了提高数据信息的分类与输出，通过生成模型完成。基于上述分析，该研究的生成对抗网络模型结构见图1。

图1 生成对抗网络模型结构图

结合图1对该研究的生成对抗网络模型进行以下介绍，在生成对抗网络模型的过程中，通常将对抗过程划分为极小、极大二元博弈问题。在一种形式上，输出的生成模型具有出色噪音处理能力，在具体工作过程中能够将输出的噪声作为输入信息，并将输入的数据信息转化为样本数据集合x～G，通过判别模型也能够输出数据信息，并将数据样本数据信息集合记作为样本x，然后将样本数据集合x进行数据输入，其中输出样本数据信息通过分布式概率D(x)进行计算。

通过判别模型输出的数据信息损失能够实现正确的信息分类，并通过平均对数概率实现网络数据信息损耗计算。在进一步计算过程中，通过对比真实经验样本以及数据生成模型进而实现均等混合数据信息的评估输出：

(7)

其中，生成模型的优化方向是使D(x)增大，D(G(z))减小。将判别模型输出的真实样本通过大概率取样，进而能够将生成模型样本概率值尽可能小；而判别模型与其理念相反。在明白两个模型的优化方向后，下面将阐述生成模型与判别模型的训练样本过程。

首先，生成模型作为训练样本的概率期望回报值V相关公式为

V=E[logD(x)]+E[log(1-D(x))]

(8)

对式(8)用积分的形式表示出来：

(9)

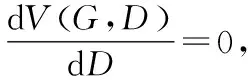
(10)

其中，Pdata表示整个对抗模型训练出数据样本的概率，PG(x)表示生成模型G训练出数据样本的概率。将式(10)带入到式(9)中并进行化简计算得到：

V=-2log 2+2JSD(Pdata(x)|PG(x))

(11)

其中，JSD表示分布相似性的散度。通过式(11)的转换得到生成模型G训练出来的样本为

2JSD(Pdata(x)|PG(x))

(12)

通过式(12)可以得出，通过组合判别模型D与生成模型G，能够进而输出生成的对抗网络模型。这是因为判别模型的优先优化更有利于目标函数快速收敛，对训练样本的速度影响更大，关于生成对抗网络优化过程如图2所示。

(a) 初始过程

(b) 优化判别模型

(c) 优化生成模型

(d) 两个模型收敛图2 生成对抗网络模型的优化过程

1.3 基于生成对抗网络的强化学习算法

1.3.1 算法总体结构框架

针对强化学习在训练样本的开始阶段，训练样本学习效率低下，收敛速度满足不了现有技术的需求，该研究将生成对抗网络模型融入本研究技术中，通过构建和设计强化学习算法提高该研究的计算能力，总体结构框如图3所示。

图3 算法总体结构框架示意图

由图3可知，在训练开始之前，根据强化学习的目标策略进行和历史数据的真实经验样本联合构建真实经验样本集。在训练初始情况下，将生成对抗网络算法模型的数学模型以及样本数据模型作为试验样本数据信息进行训练、分析，以生成新的样本，这种样本数据信息并不是历史数据所得出的真实经验，仅是理论上可行的数据样本，可称为虚拟样本[6]。虚拟样本不能直接并入真实经验样本集中，还需要通过智能体agent进行一次训练，智能体类似于人脑一样，既可以感知环境信息，也可以执行最优决策[7]。它会将好的虚拟样本并入到真实样本集当中，提高训练样本的质量。大量的经验样本不断更新状态动作，以达到全局最优。同时引入关系修正单元，基于生成对抗网络算法模型将经验样本一分为二，并算出两者的相似性[8]，在状态空间大的情况下，能显著提高强化学习的训练速度，并通过相对熵进一步提高训练样本的质量。

在生成对抗网络模型的基础下定义强化学习计算，为了更好地进行描述，需引入真实经验样本集C和奖赏函数r的概念，表示为

C=[(s,a),(s′,r)]=[x1,x2]

(13)

在后续状态函数s中，如何将该函数信息延续也是生成对抗网络模型工作的关键，通常通过生成有限的状态函数s′实现数据信息的分析与计算。在信息分析时，通过将x1、x2两者不同的数据信息产生数据关联具有至关重要的作用，其关联性通过以下公式描述：

I(x1,x2)=H(x2)-H(x2|x1)=P(x2)log2(P(x2))+

P(x2,x1)log2(P(x2|x1))=

(14)

式中，H表示熵，I表示x1、x2两者之间的差异性。通过生成对抗网络算法模型生成经验样本集G：

G=[(s,a),(s′,r)]=[G1,G2]

(15)

其中，G1、G2分别对应x1、x2。由于后续状态函数是延续上一个有限的状态函数，因此G1、G2两者具有相似性，引入相对熵(KL)的概念，用其表示G1、G2两者相似性：

(16)

式中，P数据信息对应G1，Q数据信息对应着G2。其中，p数据值对应P函数值中数据信息，q值对应Q数据信息中的函数值，i表示函数自变量。在状态空间大的情况下，能显著提高强化学习的训练速度，并且通过式(16)的延展推导，还能满足两个关键要素：

(1) 倘若P=Q，则DKL=0。

以上关键要素用文字描述，则表示通过上述函数生成的数据状态与后续数据信息生成的状态相吻合，后续数据信息是通过函数生成的后续状态与奖赏函数进行对比的工作进行对比情况的比较。在这种数据信息的相对熵能够以无限趋近的方式相似时，则表示这种方式生成的数据信息或者通过对抗网络算法模型进行训练的样本数据信息质量比较高，根据式(7)演变得出：

(17)

其中，k为上述算法模型用到的权重参数，W为上述算法模型中能够实现生成对抗网络模型的目标函数。当相对熵比较无限地接近并与0趋近时，能够使对抗网络算法模型输出的目标函数变得较小。

(2) 倘若PG=Pdata，则V(D,G)达到局部最优。

以上关键要素用公式推导，如果PG=Pdata，则根据式(10)得出D(x)=0.5，根据式(11)得出：

(18)

如果PG=Pdata，则P=Q，DKL=0，JSD=0，V(D,G)为最小值-2log2，取得局部最优。

2 实验与分析

该研究构建的实验内容为一辆四轮小车处于两面高中间底的山谷模型，其模型示意图如图4所示。

图4 实验模型

该实验模型的模拟内容为在一个光滑曲面上给四轮小车一个加速度，使其到达五角形标记的位置。但由于四轮小车初始加速度很小，四轮小车不能向左一次出发到达标记位置，需经过利用惯性，多次上下坡才能完成测试条件。在该实验模型中，实验中设置重要参数折扣因子γ=0.99，学习率α=0.001，状态s=[p，v]，动作a={+1，-1，0}。p表示四轮小车所处的水平位置，v表示四轮小车当前位置的瞬时速度。+1表示四轮小车的初始加速度向左，-1表示四轮小车的初始加速度向右，0表示不给四轮小车初始加速度。

数据试验时，通过强化学习算法的工具包OpenAI Gym进行仿真，计算机操作系统为Windows 10，64位，计算机的开发工具为Visual Studio 2019，OpenCV 3.0，该研究采用文献[5]中Q学习算法作为参照，采用基于生成对抗网络的强化学习(GRL)算法与Q学习算法在实验模型上进行训练，初始训练次数为5，两种算法需独立执行10次，得出训练次数与算法执行步数关系曲线如图5所示。

图5 两种算法性能对比图

从图5中可以看出，采用生成对抗网络的强化学习算法收敛所需的训练次数更少，这表明采用生成对抗网络的强化学习算法的系统性能更好，训练样本的速度也更快。分析其原因在于采用生成对抗网络将真实经验样本集C作为模板，生成新的虚拟样本并入到样本集C当中，大量的经验样本不断更新动作a，因此训练样本的速度快。

为了更好地表现出基于生成对抗网络的强化学习算法性能优势，该研究采用在训练次数为1和10的情况下开始生成样本，并且应用网络模型输出的对抗网络进行强化计算后的结果需独立执行10次，得出训练次数与算法执行步数关系曲线如图6、图7所示。

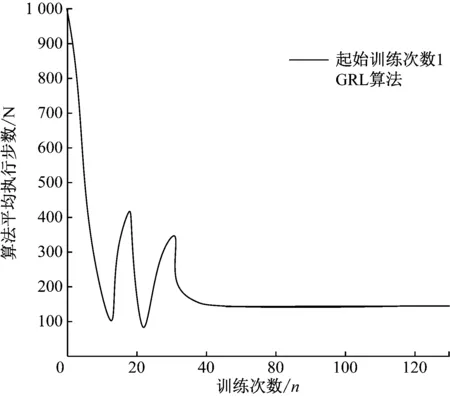
图6 起始训练次数为1的GRL算法性能图

图7 起始训练次数为10的GRL算法性能图

结合图6与图7中GRL算法的曲线图综合来看，其中起始训练次数为1的GRL算法收敛得最快，在训练次数为40左右就已收敛，而起始训练次数5和10的GRL算法分别在训练次数为60与80次的收敛。分析其原因在于采用生成对抗网络将真实经验样本集C作为模板，生成新的虚拟样本并入到样本集C当中，越早的加入生成新的虚拟样本，更新动作a的频率也就越大，因此在起始训练样本次数越低的情况下，用生成对抗网络的强化学习算法的系统性也就会更好，训练样本的速度也更快。

3 总结

该研究利用生成对抗网络模型与执行最大熵强化学习算法之间的等效性，推导使用一种特殊形式的判别模型，该判别模型利用了生成模型的似然值，从而对目标函数收敛进行了无差别估计。上述方法的输出结果表明，该研究方法的输出性能比Q算法的输出性能具有显著的提升，该算法的收敛速度比较快。这种方案也存在其他方面的不足，这仍旧需要进一步探究。