大规模MIMO 系统中基于ΣΔ 调制的一比特低功耗预编码方法

张 毅，蔡 曙，王子竟

（南京邮电大学 通信与信息工程学院，江苏 南京 210003）

在基站（Base Station， BS）上使用大规模多输入多输出（Multiple Input Multiple Output， MIMO）通信系统具有实现高谱效、高可靠性和大规模连接性的潜力，然而大规模MIMO 系统会增加基站的硬件成本和功耗。 解决该问题的一个可行方案是在每个天线单元上采用一比特模数转换器（Analog⁃to⁃Digital Converter ， ADC）／数 模 转 换 器（Digital⁃to⁃Analog Converter， DAC）。 近年来，科研人员对这种一比特MIMO 系统进行了大量的研究。 在上行链路传输场景中，现有文献主要是在信道估计和检测方面展开研究。 文献［1］对使用一比特ADC 的大规模MIMO系统中单载波和正交频分复用传输的频谱效率进行了分析，得出了可达速率下限的闭式解。 文献［2］考虑了单小区大规模MIMO 系统上行链路的信道估计和系统性能，提出一种基于Bussgang 分解的，适用于平坦衰落和频率选择性衰落的信道估计方法，然后得出平坦衰落信道中可达速率的闭式解。 文献［3］提出了一种称为一比特球形解码的低复杂度的近最大似然检测算法，在实现近最大似然检测性能的同时，降低计算复杂度。

针对下行链路传输场景，一类已有方案是通过对传统线性预编码进行量化来获得预编码［4－5］，然后分析量化噪声对系统性能的影响。 该类方案在信噪比（Signal⁃to⁃Noise Ratio， SNR）较高时会出现误比特率（Bit Error Ratio， BER）地板效应。 为改善高SNR 区域的性能，要利用数据的符号级信息。 文献［6］提出了一种对量化预编码加扰的方案，但仅适用于QPSK 信号。 基于更加复杂的非线性预编码方案，研究人员分别针对QPSK 信号［7］、16⁃QAM 信号［8］和PSK 信号［9］提出了一比特预编码方案。 对于任意的PSK 和QAM 星座图，要对QAM 星座图振幅和一比特预编码进行联合设计［10］。 为限制控制信道，QAM 星座图振幅通常用于多个符号的预编码，这种多符号耦合将导致问题维度和复杂度急剧增加。 针对这个问题，Shao 等人提出了一类基于罚函数的一阶非凸优化方法，用来优化接收端误符号率（Symbol Error Probability， SEP）［11］。 而多伦多大学Yu Wei 团队则从接收端平均SEP 与星座图振幅的关系出发［10］，利用大规模MIMO 系统中的“信道硬化”（channel hardening）现象［12］，将星座图振幅和预编码设计解耦合［11］。 这些方法可以显著地提高性能，但一比特约束往往导致需要解决大规模的离散优化问题，使设计的算法复杂度较高。

为了对具有大规模的离散约束优化问题进行简化处理，最近已有文献将时域中的ΣΔ 调制技术引入到空间域的大规模MIMO 系统中。 ΣΔ 调制是时间信号模拟／数字转换中的经典概念［13］，实现空间ΣΔ 调制技术通常由一个过采样调制器和一个负反馈环路组成。 前者产生低通信号样本，而后者将量化噪声转移到高频处。 因此，量化噪声可以很容易地从信号中分离出来。 现有的研究成果表明，将该技术应用于信道估计［14］和接收波束形成中［15］可以获得较好的性能。 Shao 等［16－17］首先考虑了基于空间ΣΔ 调制的一比特、二比特大规模MIMO 预编码方法。 在这两篇文献中，设计了预编码器来优化给定传输功率下的SNR 或SEP，仿真结果表明基于ΣΔ 调制的方法优于直接的一比特量化方法。

受上述研究的启发，本文研究了面向大规模MIMO 系统的一比特低功耗预编码方法。 在研究中，首先建立了一个具有SEP 和一比特约束的预编码和发射功率联合优化问题。 然后，引入空间ΣΔ调制将一比特离散约束转换为连续的边界约束。 然而，在ΣΔ 调制框架下，传输功率与系统的量化噪声存在耦合的关系，导致所得问题比文献［16］中只需要实现预编码器设计的问题更加困难。 为简化该问题，提出了基于空间ΣΔ 调制的迫零（Zero⁃Forcing，ZF）预编码方法，并利用SEP 和SNR 之间的关系，将该问题转化为功率优化问题。 通过推导得到发射功率的闭式解，并对此闭式解进行可行性分析，分析表明可能出现不可解的情况。 针对该情况本文又提出了一种启发式方法。 最后，通过仿真结果验证了所提方案可行性与有效性。

1 系统模型

1.1 一比特预编码系统模型

考虑一个多用户多输入多输出（Multi⁃User Multiple⁃Input Multiple⁃Output， MU⁃MIMO）下行链路通信系统。 其中，基站通过一个N维均匀线性阵列（Uniform linear array， ULA）向K个单天线用户传输信号，系统模型如图1 所示。

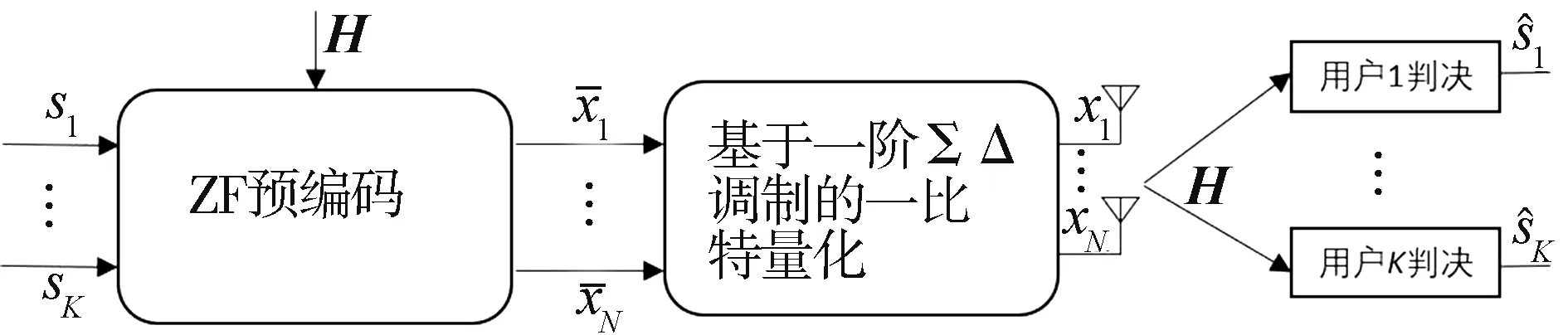
图1 系统模型

在图1 中，基站先利用信道信息H对原始信息符号s进行ZF 预编码设计，得到预编码信号x－。 然后，通过一阶ΣΔ 调制，将所得信号x－转化为一比特发射信号x，并经由平坦衰落信道发送给K个用户。在接收端，用户对接收信号进行判决，得到信息符号s＾。 通过平坦衰落信道后，第k个用户在第t个符号时间接收到的信号可以表示为

1.2 信道模型

该模型适用于多径效应的场景，如基站安装在较高的建筑物上、周围散射的数量受到限制［18］或毫米波系统［19－20］。

1.3 问题设置

式中，εk为系统预先设定的SEP，式（7b）为SEP 约束，式（7c）为一比特约束。 根据文献［21］，式（7b）中的SEP 约束可以写成

式（7d）中除p、xt、dk外，其他参数均为常数，具体推导在文献［21］中可见。

然而在大规模MIMO 系统中，解决此约束的优化问题复杂度较高，同样一比特约束式（7c）也给预编码设计带来了大量的离散优化问题，因此本文利用空间ΣΔ 调制［16－17，22－23］、信噪比和SEP 的转换关系［24］以及ZF 预编码对式（7b）和式（7c）进行转化和简化，其具体过程分别在第2 节和第3 节中给出，且通过ZF 预编码将xt转化为只跟p相关的函数，在第3 节中可见，因而优化的目标函数为p。

2 一阶ΣΔ 调制基础

文献［13，22］详细介绍了ΣΔ 调制的核心概念和技术细节。 此处对其进行简要回顾，以保障论文的完整性。

2.1 ΣΔ 调制器实现

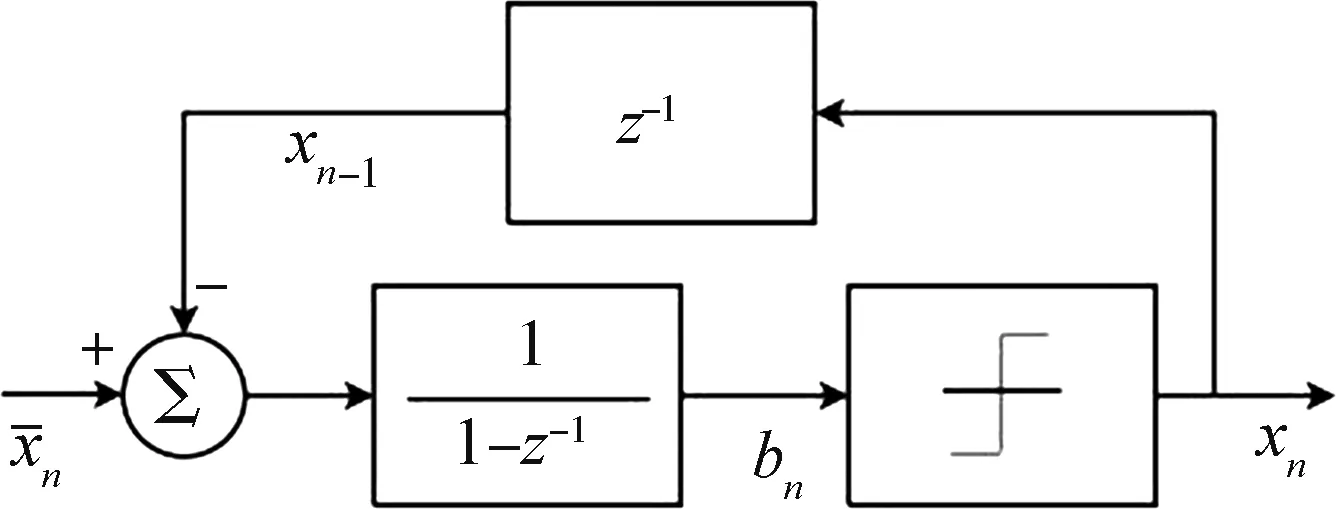
图2 一阶ΣΔ 调制框图

2.2 过载效应

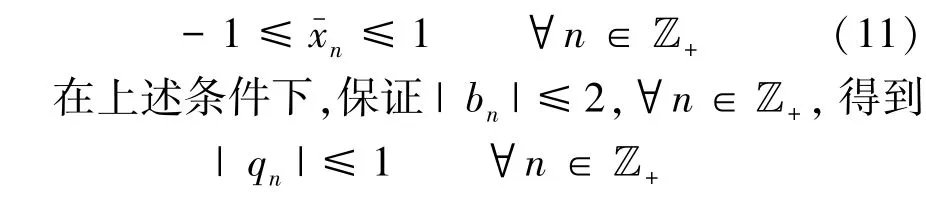
在无过载条件式（11）下，通常假设qn为独立同分布的噪声，且服从均匀分布U（－1，1）［13，16－17］。

2.3 空间ΣΔ 调制量化噪声

3 ZF⁃ΣΔ 预编码

3.1 ZF⁃ΣΔ 预编码方法

基于第2 节中的空间ΣΔ 调制可将信号模型

3.2 ZF⁃ΣΔ 启发式方法

基于上述推导可以看到，与式（19）中p2有关的γ－2可能使式（20）中的约束不可行，导致优化问题无解。 因此，本节提出一种启发式方法，将ZF⁃ΣΔ预编码信号式（14）中的归一化因子γ省略，即

4 仿真分析

图3 显示了16⁃QAM 场景下所提方案的性能情况，左侧图为误符号率性能，图中橙色点画线代表系统预设的误符号率界限，右侧图为对应的发射功率。从左侧图中可以看出在误符号率性能方面，ZF1⁃SD和ZF2⁃SD 的性能均略次于ZF1 和ZF2，原因是后者相当于是采用无限分辨率的DAC。 对于直接使用一比特DAC 量化的ZF3⁃onebit 误符号率性能很差。 从右侧图中可以看出，ZF1 比ZF2 消耗的功率较小，是由于引入了归一化因子γ对原始的ZF1 进行缩放，且ZF1 的最优解p∗小于ZF2 中最优解p～∗，导致前者功率较小。 同理，ZF2⁃SD 中最优解p～∗大于ZF1⁃SD 的最优解p∗，且经过ΣΔ 调制后的功率为2Np2，从而导致ZF2⁃SD 功率大于ZF1⁃SD。 整体上ZF1⁃SD 和ZF2⁃SD 功率大于ZF1 和ZF2，是因为前者经过ΣΔ 调制后的信号模值大于后者。 对于ZF3⁃onebit，虽然发射功率较小，但是误符号率性能很差，远不及使用ΣΔ调制的方案。 值得注意的是，在仿真中问题（21）并不是完全可解，而统计的结果均只取自可解情况下的数值进行分析，从而在一定程度上保障了图3 中ZF1 和ZF1⁃SD 的实际误符号率较低。

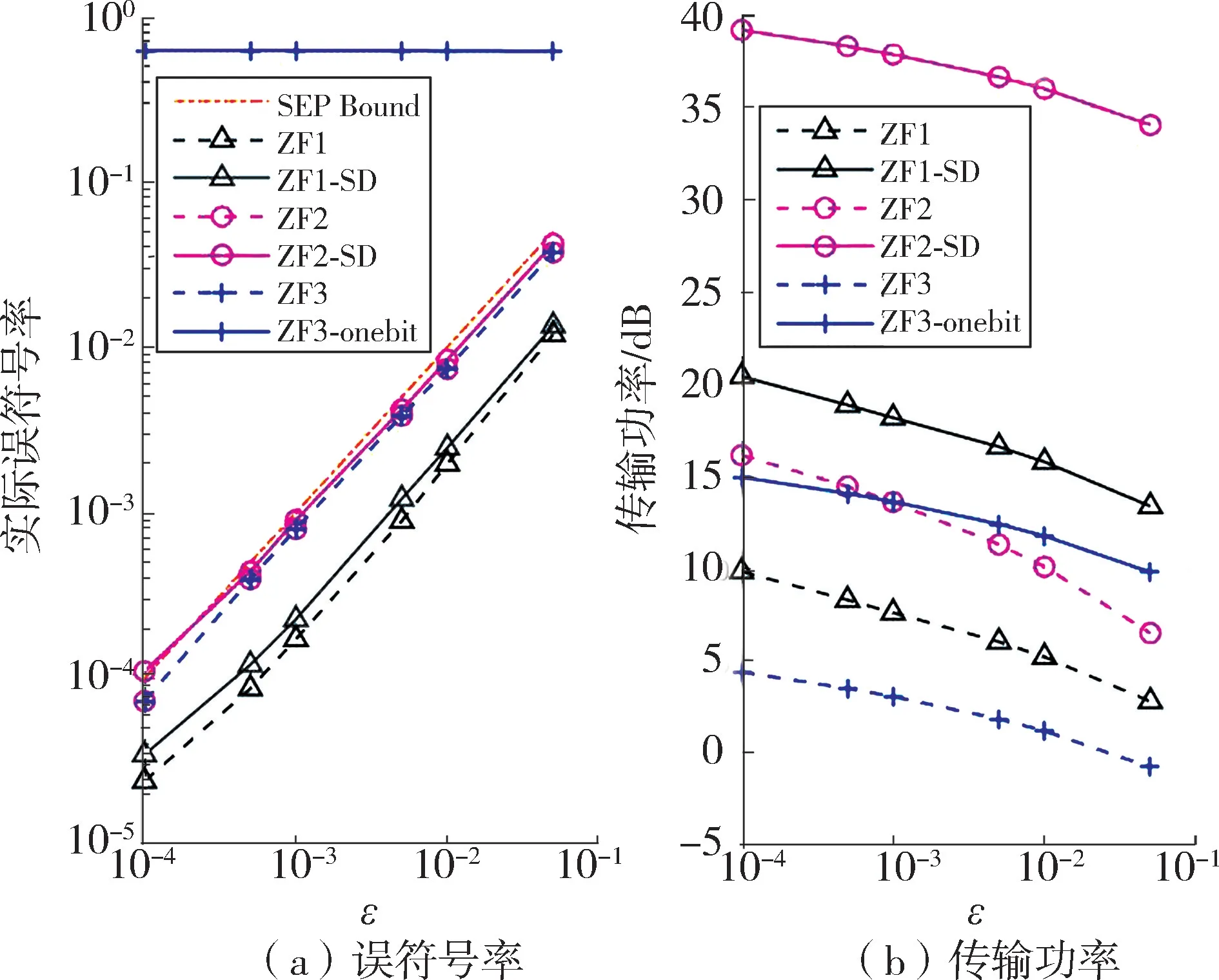
图3 16⁃QAM 场景下预编码方案性能对比

图4 显示了此场景下问题（21）的可解概率情况。 针对不可解的情况，引入的启发式方法ZF2 和ZF2⁃SD 完全可解，且能够满足系统误符号率的要求，代价是更高的发射功率。

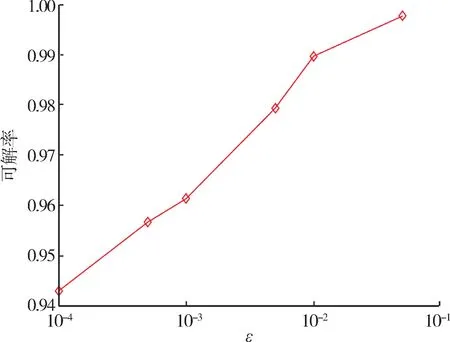
图4 16⁃QAM 场景下问题（21）可解概率

图5 显示了QPSK 场景下所提方案的性能情况，从图中可以看出QPSK 场景下所提方案总体性能与图3 类似，对于直接使用一比特DAC 量化的ZF3－onebit 性能很差，ZF1⁃SD 能够接近使用无限分辨率DAC 的ZF1，提出的启发式方法ZF2 和ZF2⁃SD 也能基本满足系统的误符号率要求，对应所需的发射功率也较高，原因和16⁃QAM 情况下分析相同。 在此场景中问题（21）的可解率为1，此处省略了仿真图。 从式（24）中也可看出，在16⁃QAM 场景下发射天线数量N不仅与用户数有关，还受到QAM 星座图大小的影响，星座图越大，所需的天线数也越大。 而在QPSK 场景下，（M－1）2＝1，发射天线数不受星座图大小影响，可解时所需天线数比16⁃QAM 场景下少，所以在同等条件下QPSK 场景中问题（21）的可解概率较好。

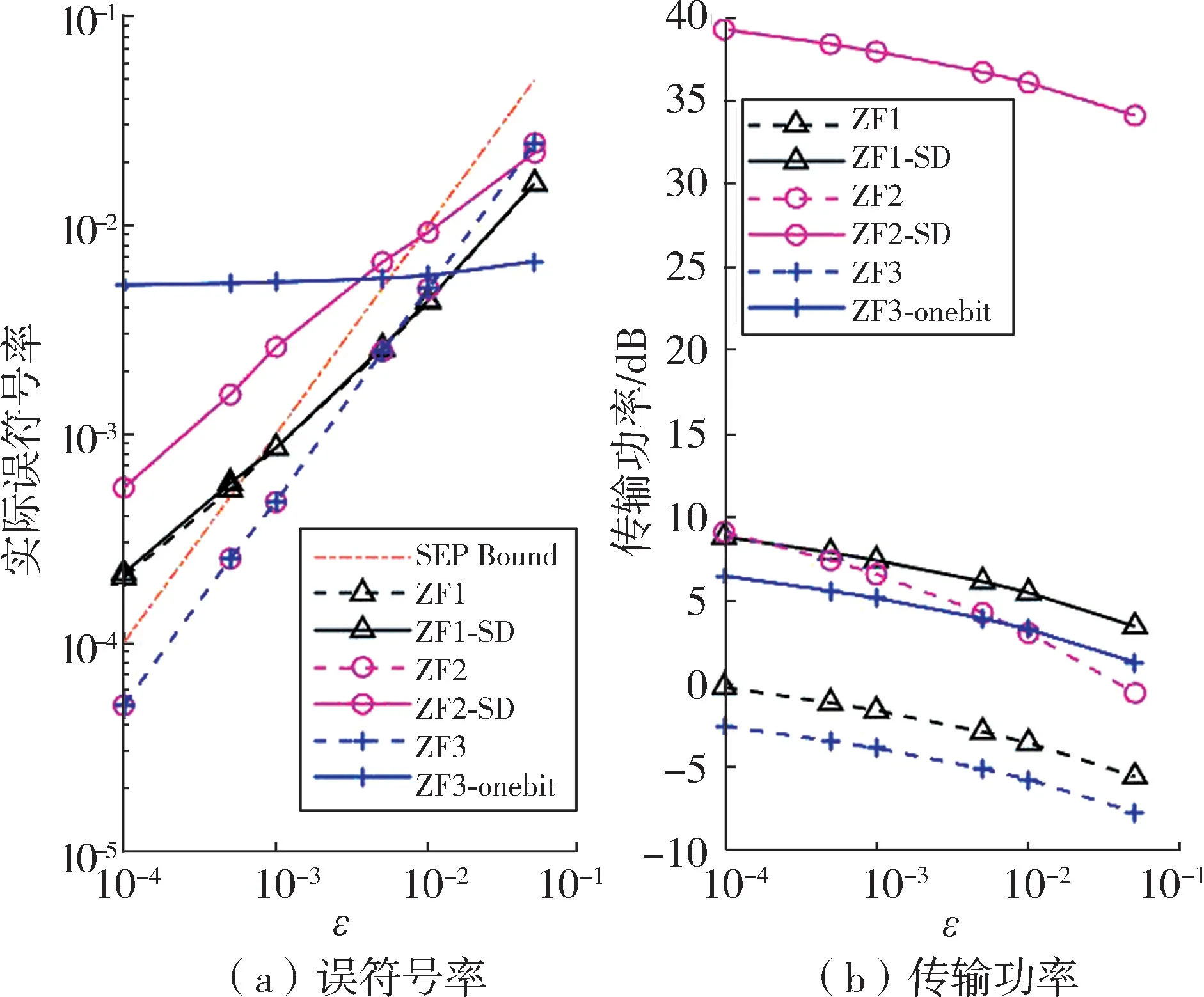
图5 QPSK 场景下预编码方案性能对比

图6 显示了QPSK 场景下问题（21）可行性随发射天线数目变化的曲线。 左侧图显示的是在不同的系统误符号率约束下，对应的问题可解概率。 从图中可以看出，随着发射天线数目和ε的增加，问题的可解概率在逐步的提高，且当发射天线数达到512根天线时，在不同的误符号率要求下问题都是完全可解的。 右侧图显示了对应的ZF1⁃SD 误符号率性能，在统计的可解情况下，实际的误符号率性能均能满足系统的要求，且随发射天线数增加、可解率增大时，曲线逐渐向预设的边界线靠近。

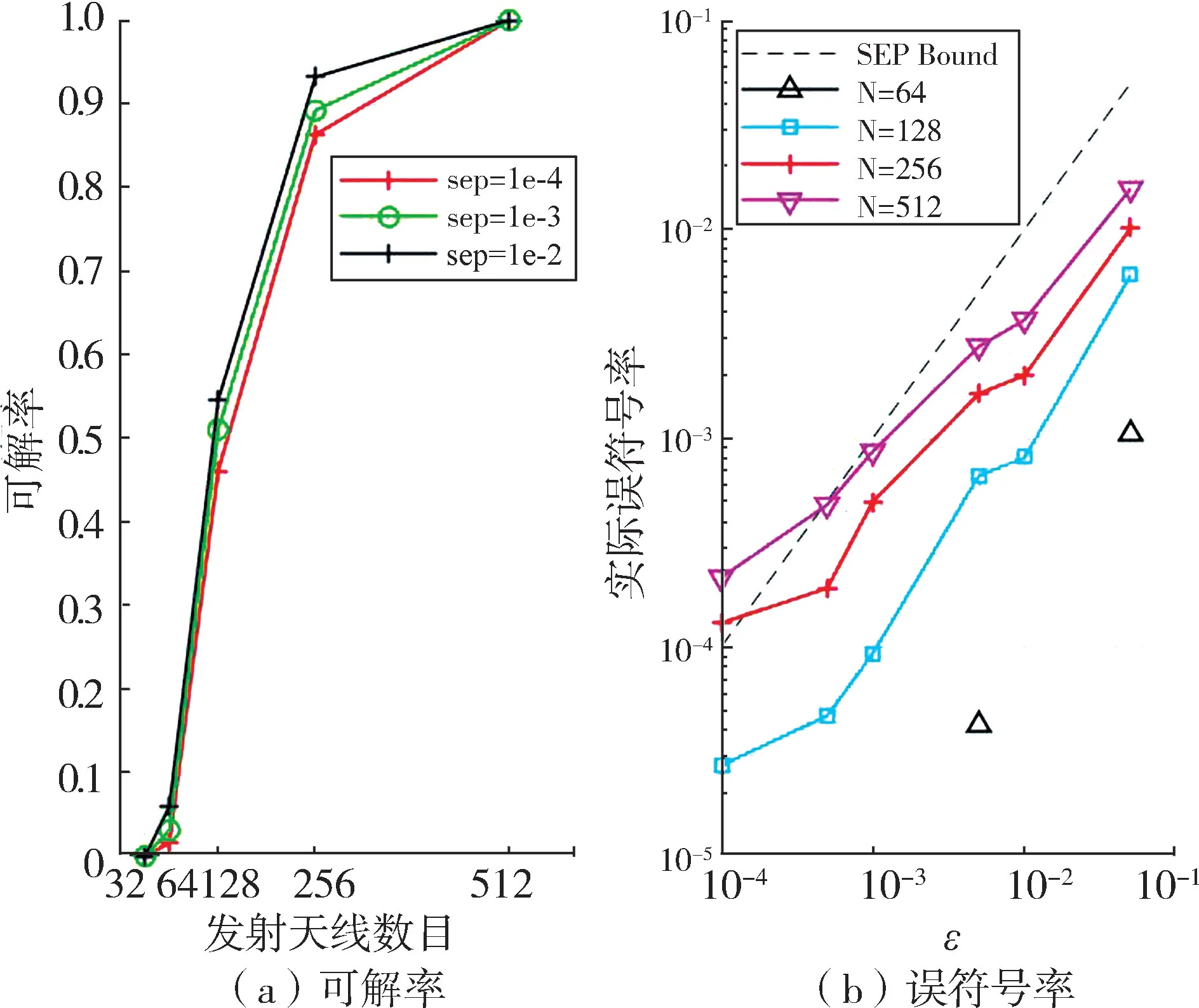
图6 QPSK 场景下问题（21）的可行性分析

5 结束语

本文研究了一种基于空间ΣΔ 调制的一比特ZF 预编码方法。 首先，提出了一个在满足系统预设误符号率约束的前提下，最小化发射功率的一比特预编码问题。 然后，引入空间ΣΔ 调制将离散的一比特约束转换为信号的边界约束，再基于ZF 预编码，结合SEP 和SNR 的关系转换，将原问题转换为发射功率控制的问题，推导出了最小发射功率的闭式解以及一种启发式方法，最后，通过仿真验证了所提方法的有效性。 文中设计的预编码方法复杂度低，对于丰富现有预编码方法，推动低能耗MIMO 通信具有重要意义。

附录