农用灌溉泵站水电转换系数测定及预测研究

钦亚洲，崔延松，钱 晖

（南通大学 交通与土木工程学院，江苏 南通 226019）

目前，我国正大力实施和推行农业水价综合改革，实现农业用水的精细化管理[1-3]。农田灌溉采用滴灌、喷洒式灌溉等高效率灌溉形式，可节约农业用水，从而改变农业用水浪费现象[4-5]。

农业用水量的准确计量是推行农业水价综合改革的重要一环。然而，由于农用小型灌溉泵站太多，对每个泵站都一一实测水泵的流量既不科学也不经济。若采用直接在水泵进水口或出水口安装流量计，往往由于测流条件不满足规定要求，使得测流结果误差很大[6]。基于此，许多地区提出采用“以电折水”的方法来计量用水量，即通过抽水时水泵的耗电量来折算水泵的实际出水量，这种方法相对简单且有效。文献[7-8]从“以电折水”计量特点及系统信息化出发，进行相关的制度设计，包括农业用水组织设计、用水定额分配方法等，形成一些有益的推进建议。

许多学者致力于建立准确的农用灌溉泵站水泵出水量和水泵耗电量关系，即准确测定“以电折水”转换系数的值[9-10]。陈彩明等[11]对浙江嘉兴南湖区1 158 个灌区泵站进行分类，选择典型泵站进行“以电折水”转换系数的率定，结果表明该地区水泵水电转换系数介于[27.79，48.82]区间（单位为m3·（kW·h）-1），且水泵型号对水泵水电转换系数有较大影响。尹世洋等[12]针对北京地区62 处农用机井灌溉区进行监测，讨论了影响“以电折水”转换系数的因素，包括水泵功率、流量、扬程，以及有无变频设备等方面。结果表明：“以电折水”转换系数与这些因素基本无关，而与地下水的埋藏深度和富水层含水量多少相关。由于上述所讨论影响因素不确定性太大，因此文献[12]只能给出水电转换系数的近似值。岳士茹等[13]基于支持向量机，考虑到地下水埋深、泵龄、井龄等因素，采用内插预测“以电折水”转换系数。囿于泵井样本量，机器学习的预测精度不高，因此文章提出了后续的改进办法。可见，“以电折水”转换系数与多个因素相关，且相关性比较复杂，目前尚未形成统一认知。

本研究提出一种新的“以电折水”转换系数的测定和计算方法。首先对测定区域内的农用灌溉泵站水泵进行分类统计，得到各水泵型号、电机额定功率、使用年限等主要参数。随后进行分类，针对典型水泵进行“以电折水”转换系数的实测确定，得到不同类型水泵“以电折水”转换系数的分布规律。此后采用效用分析对“以电折水”转换系数的两个主要影响因素进行权重分析。接着建立3 种回归分析模型，对已知的27 组水泵“以电折水”转换系数进行拟合，建立回归预测模型。最后，采用建立的3种回归预测模型，对同类型水泵的“以电折水”转换系数进行率定，并通过与水泵水电转换系数实测结果进行比较，对预测精度进行分析。

1 水电转换系数的实测

对工程区域内待测定的农用灌溉泵站水泵的型号、功率、扬程、管径、使用年限等特征参数展开调查，并对得到的结果进行统计分类，按每组典型水泵类型总数约40%比例进行“以电折水”转换系数的实测。这里为便于讨论，我们仅以两种水泵型号规格，ZLB（轴流泵）和HW（混流泵），以及水泵电机额定功率30 kW 和55 kW 为例，将灌溉水泵分为4 种类型。

分别采用水文法、容积法、仪表法和集成法等4种实测方法，对上述4 种农用灌溉泵站水泵的出水量进行测定，得到水泵10 min 的平均出水量。通过观察该水泵对应的电表，即可得到该水泵抽水期间对应的耗电量，则定义“以电折水”转换系数（简称水电转换系数）为

式中：Q 为10 min 水泵平均出水量，单位为m3；P 为对应的水泵耗电量，单位为kW·h；r 为水电转换系数，单位为m3·（kW·h）-1。

因此，该问题转化为如何准确测定灌溉水泵的出水量和耗电量。由于目前大多农用灌溉泵站实行“专变专表”，即专用变压器和专用电表，因此耗电量可通过查询电表读数获取。若能准确测定灌溉水泵的出水量，通过公式（1），即可得到精确的水电转换系数。

研究中综合采用上述4 种方法进行农用灌溉泵站水泵出水量的测量，因此能够保障实测结果的准确性。对于这4 种灌溉水泵，进行水泵效用分析时，采用72 组数据，ZLB 型、HW 型水泵各36 组。ZLB 型水泵中，ZLB500 型27 组，ZLB350 型9 组；HW 型水泵中，HW500 型20 组，HW350 型16 组。各类型灌溉水泵实测部分数据如表1 所示。

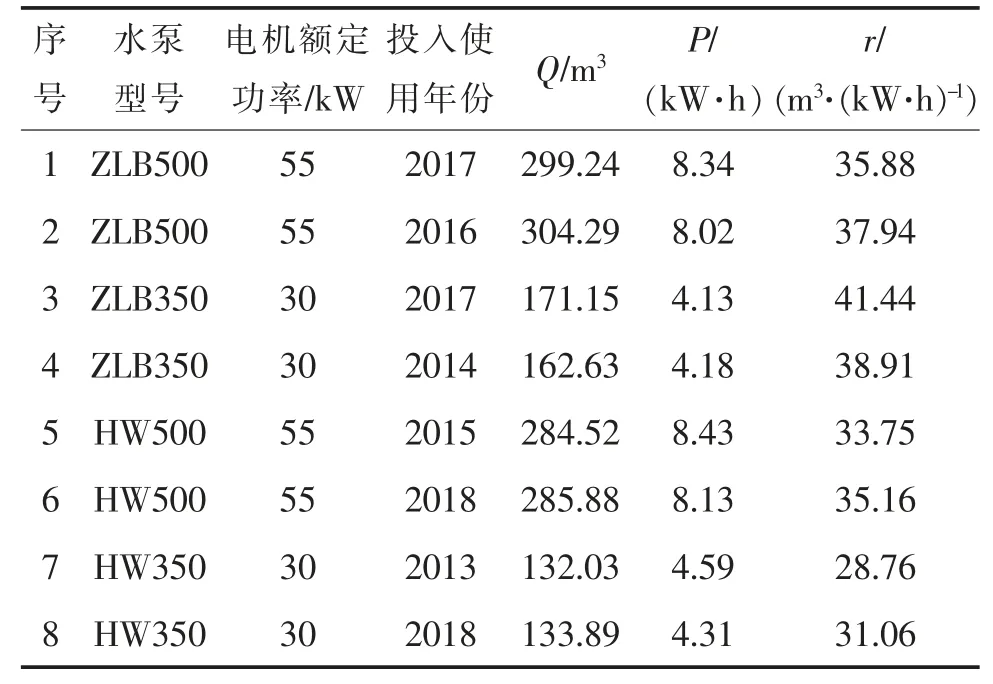
表1 实测4 类农用灌溉水泵部分数据Tab.1 Data of four types of pumps

分别统计ZLB 型灌溉水泵和HW 型灌溉水泵的水电转换系数，其分布特征如图1 所示。

图1 水电转换系数分布箱型图Fig.1 Box-plot of coefficient of"Conversion of Electricity to Water"

由图1 可见，4 类水泵的水电转换系数基本呈正态分布，无极端异常值出现，这也说明综合采用4种实测出水量方法，得到的测试结果比较准确。由图1（a）可见，对于ZLB 型水泵而言，ZLB350 型水泵的水电转换系数总体高于ZLB500 型水泵。ZLB350型水泵的水电转换系数中位数为39.43 m3·（kW·h）-1，而ZLB500 型水泵水电转换系数中位数为37.88 m3·（kW·h）-1。由图1（b）可知，对于HW 型水泵而言，HW500 型水泵，其水电转换系数中位数为36.56 m3·（kW·h）-1，高于HW350 型水泵水电转换系数中位数33.19 m3·（kW·h）-1。

同时，由图1 可获得每种类型水泵水电转换系数的大致分布区间，这为后续的水泵水电转换系数的预测和率定提供基础。ZLB500 型、ZLB350 型、HW500 型、HW350 型水泵水电转换系数的分布区间分别为[35.67，40.63]、[36.66，41.44]、[33.75，41.89]、[28.76，34.95]。若后续同类型水泵的水电转换系数率定值偏离这个分布区间太多，则说明率定值存在问题。

2 水电转换系数的效用分析

效用分析方法是用来研究消费者偏好的一种定量分析方法。它可以用来研究产品的不同属性和各属性在不同水平下，为消费者带来效用多少的一种多元统计分析方法[14-16]，目前在各个领域都有广泛的应用[17-23]。影响农用灌溉泵站水泵水电转换系数的因素目前主要有两个，即型号（包括ZLB 和HW 两个水平）和水泵电机额定功率（包括55 kW和30 kW 两个水平）。因此，主要研究这两个因素对水电转换系数的影响程度，即权重。

总效用的估计值可写为

式中：y 为在第i 个影响因素的第j 水平组合条件下，得到的水泵水电转换系数的总效用估计值；μ为在全部m 个影响因素下、全部n 个水平条件下，实测水泵水电转换系数的总平均值；βij为第i 个影响因素的第j 水平的成分效用值；xij为0，1 值，表达为

本研究中影响因素有两个，因此m=2；每个影响因素又包含两水平，因此n=2。

成分效用值βij的计算公式为

式中，μij为第i 个影响因素的第j 水平水泵水电转换系数的平均值。

对计算得到的成分效用值βij进行归一化，将每个影响因素的成分效用值最小值转化为0，其他成分效用值为与最小值之差，即

由标准化后的成分效用值，计算得到第i 个影响因素的权重为

式中，Wi为第i 个影响因素的权重。

按上述方法，计算得到水泵的水电转换系数效用分析如表2 所示。

表2 水泵水电转换系数的效用分析Tab.2 Utility analysis of coefficient of"Conversion of Electricity to Water"

由表2，计算得到水泵功率的权重为

水泵型号的权重为

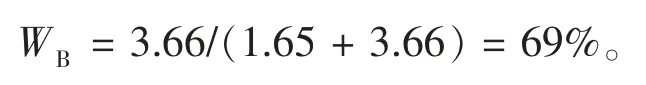
可见，对于水泵水电转换系数，水泵功率的影响所占比例为31%，而水泵型号的影响所占比例为69%，即水泵型号是确定水电转换系数的主要因素。效用分析结论与文献[11]研究结果相符。

3 水电转换系数的率定

如前文所述，工程区域内有300 多座农用灌溉泵站，我们对其中约40%的泵站水泵水电转换系数进行实测确定，对其他60%的同类型水泵，通过已得实测水电转换系数的数据资料，建立回归模型进行率定。这种方法的优点：一是经济性，避免因同类型水泵的重复测定而增加人力、物力花费；二是提高效率，缩短泵站水泵水电转换系数的测定工期。

由于农用灌溉泵站投入使用年限较久存在老化现象，因此可能会影响泵站水泵的出水量及耗电量，从而间接影响泵站水泵水电转换系数的值。因此，考虑水泵水电转换系数与泵站投入使用年限之间的关系，进而采用这种相关关系对同类型水泵（即同类型、同功率）的水电转换系数进行预测和率定，从而大大减少水电转换系数实测的工作量，提高工程经济性。为此，以ZLB500 水泵为例，基于实测的27 组数据，采用3 类函数进行数据的回归分析，包括线性回归、幂函数回归和对数回归。得到的回归方程、判定系数（R2）、系数的概率（p）分别如下所示：

线性回归：

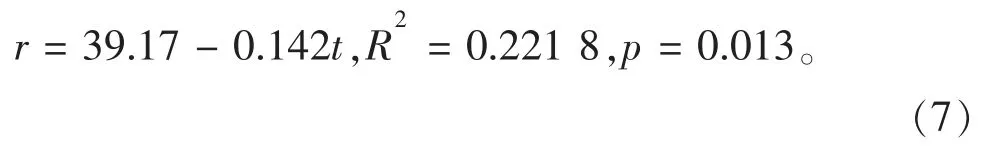
幂函数回归：

对数回归：

回归分析结果如图2 所示。回归分析发现3 种回归模型的判定系数均不高，表明实测值的离散性比较大；但系数p 值均远小于显著性水平0.05，说明泵站水泵的水电转换系数与水泵使用年限之间具有很强的相关性。但可能由于还存在其他未知影响因素，使得判定系数较低。

图2 水泵水电转换系数回归分析Fig.2 Regression analysis of coefficient of"Conversion of Electricity to Water"

采用另外10 组实测ZLB500 型、电机额定功率为55 kW 泵站水泵的水电转换系数数据，检验所得回归模型的准确性。比较水电转换系数的率定值与实测值，并给出相对误差，结果如图3、表3 所示。

由图3 和表3 可见，采用3 种回归模型对另10组农用灌溉泵站水泵水电转换系数进行预测，预测值和实测值最大相对误差为8%，小于规定相对误差设定值10%，能够满足实际使用的要求。

图3 各模型的预测效果Fig.3 Prediction of three regression models

表3 水电转换系数的率定值及相对误差Tab.3 Prediction and relative error of coefficient of "Conversion of Electricity to Water"

4 不足与改进

通过上述研究发现，准确测定和计算农用灌溉泵站水泵水电转换系数是一个比较复杂的问题，涉及各影响因素的确定、影响程度的衡量以及计算方法的选择等。目前针对华北地区的水电转换系数研究较多，但由于华北地区农业灌溉普遍采用机井抽取地下水的方式，因此影响水电转换系数的主要因素为地下水埋深、富水层含水量等。而平原地区如江苏，农业用水主要采用抽取地表水的方式，因此影响水电转换系数的因素与华北地区显著不同。目前对平原地区的农用灌溉泵站“以电折水”的研究主要集中于建立和完善制度建设方面，技术方面的研究比较少。因此，有必要在后续的研究中，进一步积累实测数据资料，分析和发现潜在的影响变量，对水电转换系数从理论分析上进行完善，在预测精度上进一步提高。

5 结论

“以电折水”是目前多地区提出的测定农业用水量的方法，优点在于简便易行、花费较少。采用4种方法，即水文法、容积法、仪表法和集成法，对工程区域内约40%的农业水泵进行实测，并对实测结果进行统计，得到每种型号水泵的水电转换系数整体分布。结果表明：ZLB350 型水泵水电转换系数总体高于ZLB500 型水泵，HW350 型水泵水电转换系数总体低于HW500 型水泵。

对水泵水电转换系数进行效用分析，结果表明：水泵型号、水泵功率两个影响因素对水泵水电转换系数的影响权重分别为69%和31%，水泵型号对水电转换系数有更大影响。

最后，采用ZLB500 水泵实测27 组数据建立3种回归模型，采用另外实测10 组数据进行模型验证。结果表明：3 种回归模型的预测结果最大相对误差仅8%，小于10%的相对误差规定值，能够满足使用精度要求。