不同直径砂管灌土壤水分运移分布研究

许春娟，贾生海，赵 霞，白有帅，曹 睿，王艳琴，杨耀峰

(1.甘肃农业大学水利水电工程学院，甘肃 兰州 730070；2.民勤县给排水管理站，甘肃 民勤 733300)

水资源短缺是影响河西绿洲灌区林果业可持续发展的重要因素[1]。滴灌是目前水分利用最高效的灌水技术之一[2]，有地表和地下滴灌2种，滴灌相比其他灌溉方式有明显的优势，但也存在缺点，例如滴头堵塞、土壤盐渍化、限制根系更好发展等问题[3-4]。有学者对地下滴灌进行了探究，Meshkat等[5-8]在1997年提出了间接地下滴灌，采用专用打孔器取出滴头下方的一部分土壤，形成一个圆柱形的洞装入渗透性更强的材料，如粗砂[9]。因此有了砂管灌(Sand Tube Irrigation，STI)，砂管灌是在滴灌技术的基础上形成的新型地下滴灌技术，主要运用于稀植作物，可以将水分更快更直接地输送到作物根部，即不增加土壤表层含水率也减少了地表蒸发[10]，避免了滴头堵塞。

有学者对砂管灌进行了探究，Meshkat等[5]通过实验测定出灌水后4d内地表滴灌的水分蒸发约有30%，而砂管灌只有3.7%。Meshkat等[6]通过研究得出进行连续灌溉后4d内在0.2～0.55m的深度上，砂管灌下的土壤水分明显高于地表滴灌法。Yanni等[11]采用与Meshkat相类似的方法将垂直砂覆盖(Gravel Vertical Mulching GVM)运用于果树的灌溉试验研究，得出相同的灌水量条件下，灌溉结束后14d内的根层含水量GVM方式要明显高于普通地表滴灌方式。孙三民等[12]试验得出了间接地下砂管灌相比滴灌节水增产效果显著，骏枣的产量随着砂管灌导水装置埋深的增加增大。砂管灌的直径也直接影响水分在土壤中的运移与分布[13]，土壤湿润锋不仅可以反映灌溉水量是否满足要求还可以反映灌溉质量[14]。近几年砂管灌直径参数对土壤水分入渗影响的研究鲜有报道，因此研究砂管灌不同直径参数下的土壤水分运移规律，确定砂管灌的最优参数组合，对于干旱地区林果业节水灌溉提供理论依据以及砂管灌的推广应用具有重要意义。

1 材料与方法

1.1 试验场地与装置

整个试验由土箱和供水装置2部分组成，场地为甘肃农业大学水利水电工程学院土工实验室。土箱为长宽高120cm×55cm×75cm的长方体透明玻璃箱，透明的土箱外壁用来观测和记录湿润锋分布情况，取入渗形成的1/2湿润锋来研究。通过马氏瓶提供恒压稳定水源，滴灌管连接马氏瓶用密封胶密封出口，在其上镶嵌滴头固定在砂管中心点处。滴头流量为固定值4L/h，试验所用土壤取自民勤县勤锋林业试验站枣树种植基地，土壤类型为砂壤土，土壤容重为1.5g/cm3。将土样按实测土壤的干容重过2mm筛之后自然风干分层填入(每层5cm)，在填土过程中将不透水边界PVC管(半圆柱)高20cm填入土箱长边一侧1/4处，待土样装填完毕、平整表面后，将粒径为3～5mm的粗砂填入半圆柱体内捣实随后将PVC管缓慢抽出，形成边界完全透水的砂管导水装置，如图1所示。

图1 砂管布置图

1.2 试验设计

砂管灌入渗试验中，导水装置高度20cm为完全透水边界。为探究砂管灌不同直径大小对土壤水分入渗的影响，设计3个砂管灌直径d=5cm(T1)，d=10cm(T2)，d=15cm(T3)。对T1、T2、T3 3个处理下的砂壤土水分运移进行研究，滴头流量为固定值4L/h，每个处理设置重复。

1.3 观测内容

湿润体形状：砂管灌试验开始后用秒表计时，分别在3、10、30、60、120、180min时记录灌水量，用记号笔在玻璃土箱外侧描出每个时刻对应的湿润锋运移曲线。灌水结束时采用剖面法结合沿湿润线在地表及竖直观测面湿润线特征点处插细针(至少5个)[15]，用直尺测量每个特征点的纵横坐标绘制成图。湿润体土壤水分：入渗结束24h后迅速用直径1cm土钻在砂管外侧固定一侧取土，水平和垂向均以5cm为间隔取土装入铝盒，土壤含水率采用烘干法测定。

1.4 数据处理

用Microsoft Excel进行数据分析，Origin 2018进行绘图。

2 结果分析

2.1 不同砂管灌直径对土壤湿润锋的影响

为方便观测湿润锋变化规律，取1/2实测的湿润体运移曲线对称得出整个湿润体。如图2所示为砂管灌直径为5cm时的湿润体形状，在10min时地表出现了湿润，在3min时没有观察到湿润锋，可能由于滴头附近粗砂和土壤比较干、砂管直径较小。湿润体形状在10min之后近似为垂向作为长半轴扁率比较大的椭球体直至入渗结束。入渗结束后在24h时观察土壤水分再分布情况，地表形成的湿润体长轴为17cm、短半轴为20cm。垂向最大入渗距离为35cm，横向最大入渗距离为21.6cm。

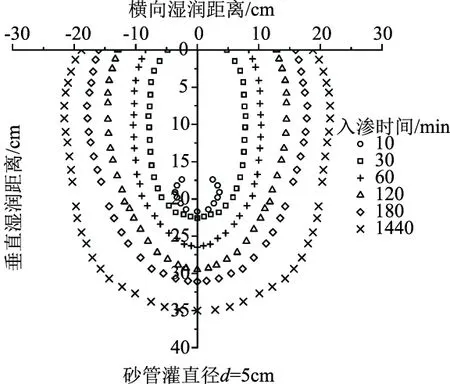
图2 砂管灌直径d=5cm湿润体形状

如图3所示为砂管灌直径为10cm时的湿润体形状，在入渗初期，同一时间间隔内水平入渗距离大于垂向入渗距离，湿润体形状近似为平卧的椭球体且扁率在不断减小。在60min时湿润体形状近似为圆球形，水平入渗距离和垂向入渗距离分别为13cm和13.1cm。60min之后湿润体形状为垂向变为长轴的近似直立的椭球体且扁率有增大趋势。这可能是由于入渗初期土壤基质势起主要作用加上砂管的影响，水没有完全浸润砂管，横向的砂管半径为5cm小于垂向的砂管深度20cm，横向的粗砂透水性大于垂向粗砂透水性和基质势作用，使得横向入渗距离大于垂向入渗距离。在60min之后水分已完全浸润整个砂管垂向的粗砂透水性完全大于横向，基质势逐渐减小重力势增大，出现了垂向入渗距离大于横向入渗距离的情况。直至入渗结束，在24h时观察湿润体再分布情况，垂向入渗距离最大达到44.4cm，水平入渗距离最大达22.3cm，没有出现地表积水。

图3 砂管灌直径d=10cm湿润体形状

如图4所示为砂管灌直径为15cm时的湿润体形状，湿润体的形状和砂管直径为10cm时基本相同，也是在60min时近似为圆球形，之前和之后分别为横向和垂向为长半轴的椭球体。在24h时观察湿润体再分布情况，垂向入渗距离最大达到45.3cm，水平入渗距离最大达23.7cm，没有出现地表积水。停止灌溉后24h内不同直径砂管灌土壤水分运移均有再分布情况，水分再分布后湿润体近似呈直立的椭球体，水平入渗速率均大于垂向入渗速率。分析可能是由于停止灌水后水分再分布过程，主要由水势梯度和重力势决定[16]。

图4 砂管灌直径d=15cm湿润体形状

2.2 砂管灌条件下入渗距离与时间的关系

在砂管灌不同直径条件下土壤水分入渗过程中，将垂向方向和水平方向上的入渗距离与时间进行曲线拟合，如图5所示为砂管灌直径10cm时水平和垂向湿润锋运移距离与时间的关系，入渗初期，水平入渗距离大于垂向入渗距离，在60min时垂向和水平入渗距离基本相同，最终垂向入渗距离大于水平入渗距离，二者与时间均有良好的幂函数关系[17]。由拟合曲线的横向R2=0.99375和垂向R2=0.99447大于0.99可知，直径为5、10、15cm砂管灌土壤水分入渗过程中的入渗距离与时间均有显著的相关性。

图5 入渗距离与时间的关系

横向：x=48512t0.2458R2=0.99375

垂向：y=249034t0.40325R2=0.99447

2.3 砂管灌条件下入渗速率与时间的关系

如图6所示为砂管灌直径为10cm时入渗速率和时间的关系，土壤水分入渗过程中，砂管灌直径为5、10、15cm时水平和垂向入渗速率都随着时间呈现3种变化规律，入渗初期入渗速率快速下降，入渗中期入渗速率缓慢下降，入渗后期入渗速率基本趋于稳定。砂管灌直径为15cm时的入渗速率最大，水平入渗速率最大达2.67cm/min，在入渗开始至60min时水平入渗速率明显大于垂向入渗速率，60min之后垂向入渗速率大于水平入渗速率。砂管灌直径为10cm时最大入渗速率为1.97cm/min。

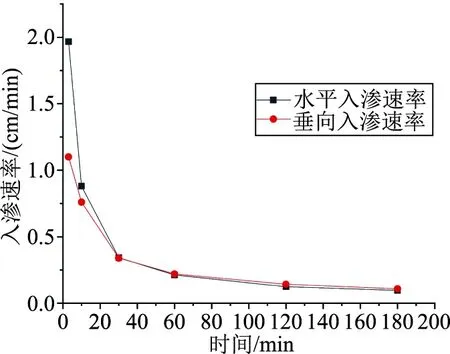
图6 T2处理下入渗速率与时间的关系

2.4 砂管灌条件下湿润体含水率分布规律

取直径10cm砂管灌的含水率数值分析湿润体含水率分布规律。含水率在水平和垂向方向上均采用平均含水率来分析，水平方向平均质量含水率是将竖直方向上的土壤含水率取平均值[18]。将砂管底部垂向向下20cm处作为出水口，土壤含水率的变化与出水口的距离密切相关，如图7所示为含水率随水平距离的变化趋势，随着距离的增大逐渐减小，距出水口越远含水率越小，在出水口处土壤含水率最高为11.47%，距离出水口20cm处的土壤含水率最低为3.08%。将平均土壤质量含水率随水平距离的变化关系进行二次函数拟合，得出：

图7 土壤含水率随水平距离的变化

θm=-0.00529x2-0.30718+11.41483

(1)

R2=0.99801

式中，θm—质量含水率，%；x—湿润锋水平运移距离，cm。

拟合曲线的相关系数R2=0.99801大于0.99表明拟合关系达显著水平[19]，平均土壤质量含水率和湿润锋水平运移距离之间具有良好的二次函数关系。

如图8所示为垂向方向上的平均土壤质量含水率变化曲线图，将水平方向上的土壤含水率取平均值求得。同样将砂管底部垂向向下20cm处作为出水口，出水口向上取为负、出水口向下取为正。垂向的平均土壤含水率的变化与距离出水的位置紧密相关。距离出水口向下5cm处土壤含水率达到了最大值约13.85%，在出水口附近形成了高含水率区，距离出水口越远含水率越小。表面的土壤由于没有地表积水为干土含水率最小约为1.09%，最下侧土壤在距离出水口30cm处为干土土壤含水率也为1.09%，下侧被湿润土壤的最小含水率约为5.36%。垂向向下的平均土壤质量含水率分布规律为距离出水口向下的含水率值整体大于向上的含水率值，这可能是由于重力和砂管的作用，更有利于水分向下扩散，使得距离出水口向下的含水率高于向上且最大值出现在距离出水口向下5cm处。将平均土壤质量含水率随垂向距离的变化关系用二次函数进行拟合，得出：

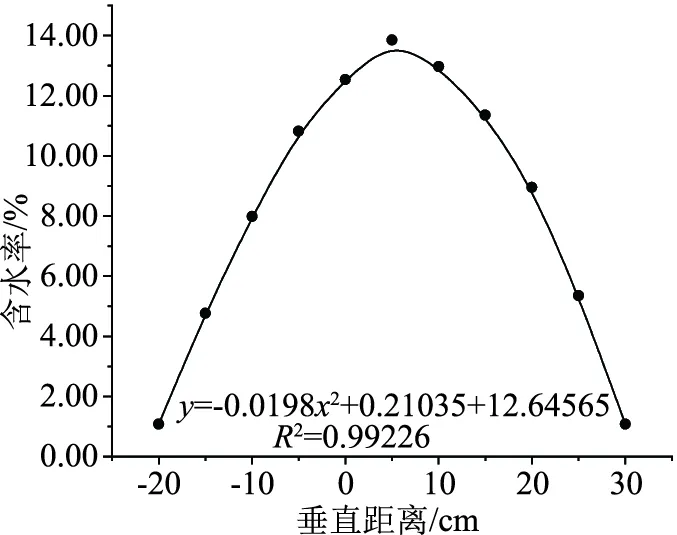
图8 土壤含水率随垂向距离的变化

θm=-0.0198y2+0.21035y+12.64565

(2)

R2=0.99226

式中，θm—质量含水率，%；y—湿润锋垂向运移距离，cm。

由拟合曲线的相关系数R2=0.99226大于0.99表明拟合关系达显著水平，平均土壤质量含水率和湿润锋垂向运移距离之间具有良好的二次函数关系。

3 结语

在滴头流量为4L/h，灌水时间持续3h，不同直径砂管灌土壤水分入渗规律基本一致；且随着时间推移，水分在垂向的运移距离大于水平方向的运移距离。湿润体的形状由最初的近似椭球体变化为近似圆球体再到最后的近似椭球体。最后垂向入渗距离大于水平入渗距离，水平和垂向入渗距离均与时间有极显著的相关性，可表示为幂函数关系。入渗速率为最终的垂向入渗速率大于水平入渗速率。

在砂管灌条件下水平方向平均土壤质量含水率和垂向方向平均土壤质量含水率均与距离有显著的相关性，可表示为二次函数关系。土壤含水率在水平和垂向均表现为靠近水源处最大，距离水源处越远含水率逐渐减小。在垂向方向上从出水口向下的含水率均大于向上的含水率。随着入渗量的增加，垂向向下的粗砂透水性加上水分的重力作用大于土壤的毛细管力，使得垂向向下水分入渗速率大于垂向向上入渗速率，出现了下部含水率高于上部的情况，靠近出水口处各点的含水率比较高。

综上所述，T1处理下在入渗3min时没有观察到湿润锋，在10min时地表出现了湿润锋，造成了土壤表面水分蒸发。T2和T3处理直至入渗结束都未出现地表湿润。T3处理下的土壤水分入渗过程与T2处理基本相似，入渗达到的水平和垂向最大湿润距离略高于T2处理，水平方向增加了6.3%，垂向方向增加了2%，且砂管直径15cm相比10cm增大了工作量和成本，不适宜采用。将砂管直径10cm运用于河西绿洲地区枣树的灌溉中，以期为地下砂管灌在河西绿洲地区枣树种植中的试验和推广以及干旱地区林果业节水灌溉提供理论依据。