求解大规模矛盾方程组的最小二乘支持向量机算法
郑素佩,闫佳,宋学力,陈荧
(长安大学理学院,陕西 西安 710064)
0 引 言
在求解范围内无解(解为空集)的方程组称为该范围内的矛盾方程组。矛盾方程组在实际生活中应用广泛,通常采用最小二乘法求解,其基本思想是寻找一组解,使得方程组两端的偏差向量的2-范数平方最小。近年来,基于最小二乘法的新算法不断涌现,如JIANG[1]系统阐述了最小二乘有限元法;李玉良等[2]依据圣维南原理,提出了基于最小二乘法的复杂局部边界结构载荷误差消减算法。
随着信息技术的发展,实际遇到的矛盾方程组规模都较大。当方程组规模过大时,用传统的最小二乘法求解,计算、存储均较复杂,且误差较大,需要寻找更好的算法。例如,将最小二乘与随机算法相结合[3],运用机器学习改进最小二乘法的计算精度[4]等。
机器学习是一门多领域交叉学科,以计算机为工具模拟人类的学习方式,适用于大规模数据处理,可很好地解决非线性问题。其中支持向量机(support vector machine,SVM)[5-6]因具有出色的泛化能力和较强的样本适应能力应用广泛。SUYKENS等[7]从机器学习的损失函数入手提出的最小二乘支持向量机(least squares support vector machine,LS-SVM)算法,求解精度大幅提高,并不断被用于解决实际问题。例如徐锋等[8]提出了基于LS-SVM积分型辨识样本结构的船舶操纵运动的在线建模。SHARMA等[9]为提高工程造价预测的准确性,提出了基于LS-SVM的工程造价预测模型,该模型预测精度高,结果稳定,相对误差在7%内。赵庆志等[10]应用LS-SVM实现了对未来降雨的预测,可准确预测99%的降雨事件。鲜有报道涉及基于LS-SVM算法求解具有实际背景的大规模矛盾方程组的研究。鉴于此,本文采用LS-SVM算法对大规模矛盾方程组进行数值求解,给出求解过程,将其应用于若干具体算例,并对结果进行分析和比较。
1 矛盾方程组的最小二乘解


2 机器学习法求解矛盾方程组
将最小二乘法运用于SVM,在优化问题的目标函数中使用2-范数,用等式约束条件代替SVM标准算法中的不等式约束条件,得到LS-SVM[7]。SVM与LS-SVM的区别主要表现在:
(1)优化问题的构造不同,SVM采用的目标函数为误差因子的一次项,约束条件为不等式约束;LS-SVM具有最小二乘的性质,采用的目标函数为平方项,约束条件为等式约束。
(2)在求解二次规划(quadratic programming,QP)问题时,SVM的变量维数与训练样本的个数相同,求解过程中矩阵元素的个数是训练样本个数的平方,当数据规模较大时,SVM的求解规模也随之增大;LS-SVM则通过求解线性方程组得到最终的决策函数,在一定程度上求解难度较SVM大大降低,求解速度更快,适用于求解大规模问题。
(3)SVM可通过求解QP问题获得理论上的全局最优解,因为大部分的Lagrange乘子为零,最终的决策函数只能依赖于少量数据,即支持向量,从而体现了SVM中解的稀疏性特点。LS-SVM采用误差平方项以及等式约束条件来优化问题,将SVM中的QP问题转化为求解线性方程组,使得Lagrange乘子与误差项相关,其最终决策函数与所有样本相关。
因此,LS-SVM在计算时间、计算复杂度和精确度上均优于SVM。鉴于此,本文运用LS-SVM求解大规模矛盾方程组。
2.1 LS-SVM


2.2 算法步骤
第1步将矛盾方程组求解问题转化为凸优化问题,建立优化目标函数;
第2步构建Lagrange函数,利用Lagrange乘子法将优化问题转化为对单一参数α的求极值问题;
第3步将求极值问题转化为求线性方程组;
第4步将解代入原始模型即为训练所得线性模型;用φ(x)表示将x映射后的特征向量,得到相应的最终LS-SVM非线性回归函数;
第5步将数据代入模型,得到实验结果,即最终预测值。
3 数值算例
实际问题包括单变量问题和多变量问题,数据一般分为线性和非线性两大类,运用LS-SVM进行算例分析,数据量为1000~7000,以验证算法性能。算例1~算例3中数据是通过随机取样方法产生10-3~10-2的振幅,将原函数值加上或减去该振幅得到的。算例4~算例8中数据集均来自加州大学欧文分校机器学习数据库(UCI Machine Learning Repository,http://archive.ics.uci.edu/ml/index.pdf)。
为便于对比,所有数值算例结果均显示部分数据,且分为上、下两图,上图为训练集预测结果,下图为测试集预测结果,图中纵坐标Yt表示最终预测值。训练集主要用于训练模型,测试集主要用于测试模型的优劣。
3.1 单变量线性矛盾方程组求解
算例1函数上下扰动所得数据为y*。
该算例属于一元线性问题,共5000组数据,随机选取3500组为训练集,剩余1500组为测试集,进行两组实验,实验1和实验2的测试集分别为,(xi,xi/5-600),i=1,2,…,1500。如图1所示,在实验1中,R2达0.962,在实验2中,R2达0.999,拟合效果非常好。结果表明,在大数据量的情况下,拟合度依然较高。
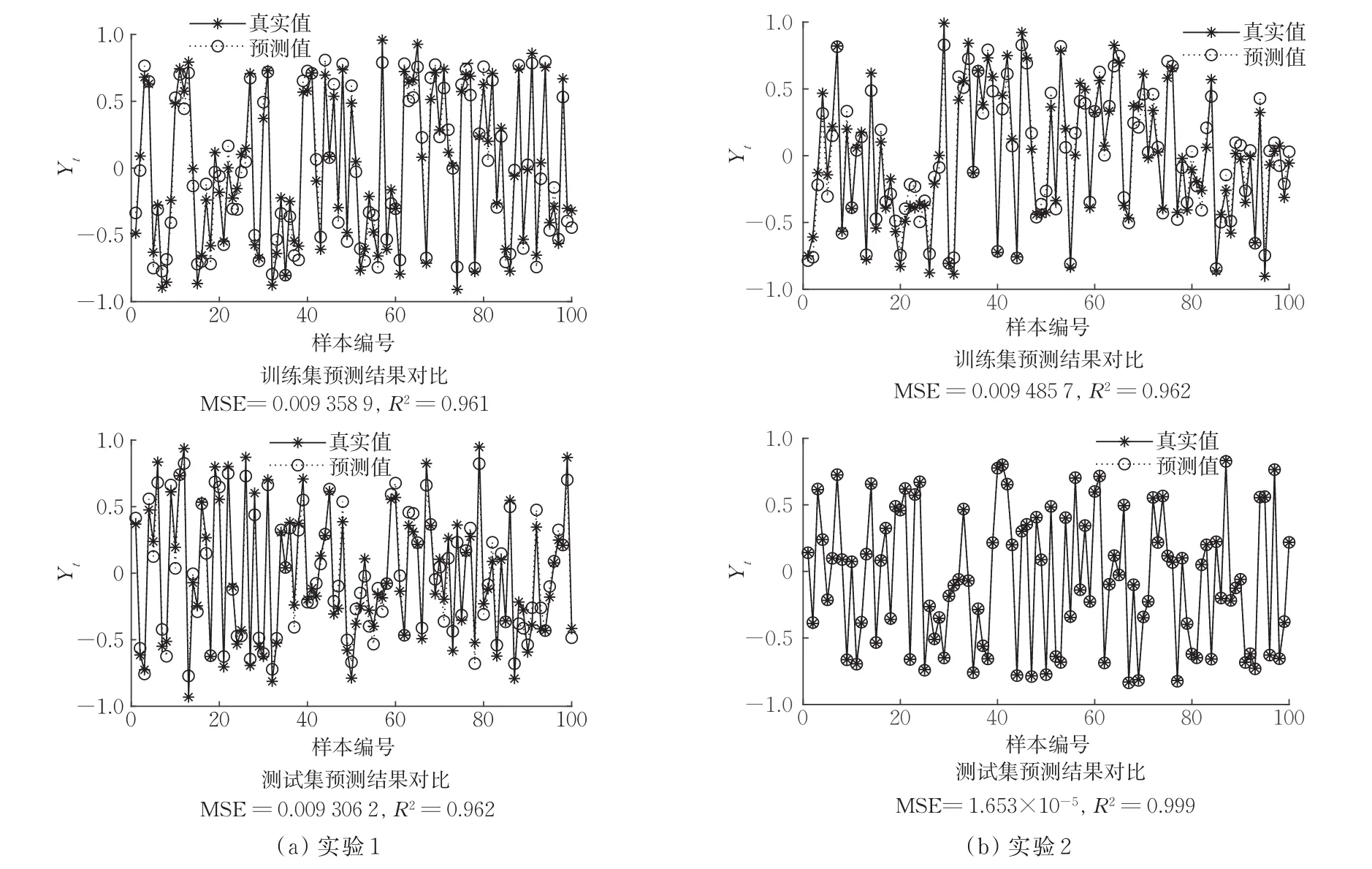
图1 算例1数值结果Fig.1 Numerical results of example 1
3.2 多变量线性矛盾方程组求解
算例2函数y=3|x1|-2|x2|+3x3上下扰动所得数据为y*。
该算例属于三元线性问题,共5000组数据,随机选取4000组为训练集,剩余1000组为测试集。如图2所示,两次实验的R2均为0.990以上,拟合效果非常好。结果表明,大数据量并不影响多元线性问题的拟合效果,可以很好地对原函数进行近似。

图2 算例2数值结果Fig.2 Numerical results of example 2
3.3 单变量非线性矛盾方程组求解
算例3函数y=10 sin(x)上下扰动后所得数据为y*。
该算例属于一元三角函数拟合问题,共6000组数据,随机选取4500组为训练集,剩余1500组为测试集,满足LS-SVM对训练集和测试集的要求。实验1的测试集真实值为y*,实验2的测试集真实值为y,预测结果如图3所示。可知,实验1的R2=0.837,表明三角函数具有较好的拟合效果。实验2的R2=0.845,表明y具有较好的拟合效果。
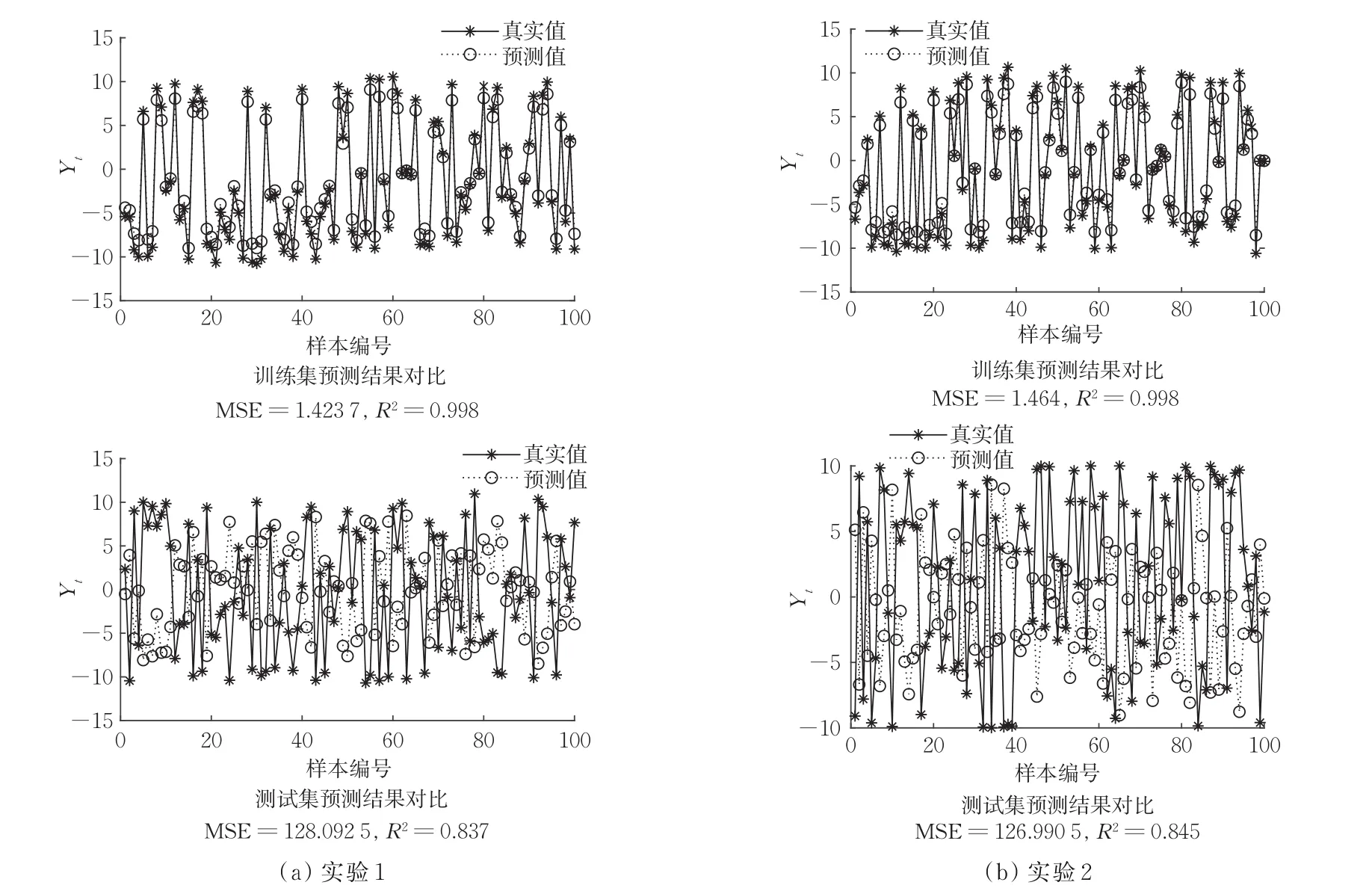
图3 算例3数值结果Fig.3 Numerical results of example 3
3.4 多变量非线性矛盾方程组求解
算例4Airfoil_self_noise数据集预测。
该数据集来自美国航空航天局(NASA)在消声风洞中进行的二维和三维翼型叶片剖面的一系列空气动力学和声学试验。其中,机翼的跨度、观察者的位置不变。共1503组数据,5个属性值,随机选取1150组为训练集,其余353组为测试集。预测结果如图4所示,经过多次实验,最佳R2=0.889,拟合效果较好,本算例数据量较小,实验结果较好,可以采用该模型进行数据预测。

图4 算例4数值结果Fig.4 Numerical results of example 4
算例5gt_2011数据集预测。
该数据集包含由11个传感器测量的36733个实例,是土耳其西北部地区燃气轮机1 h内的数据汇总(平均值或总和),目的是研究烟气排放,即一氧化碳和氮氧化物。本实验仅选取2011年的数据,共7411组,输出值为一氧化碳排放量。随机选取6000组为训练集,其余1411组为测试集。预测结果如图5所示,R2=0.909,拟合效果较好,可以根据此模型预测气体排放量。该算例的数据量较算例4大幅增加,有7000多组数据,但预测结果并未变差。
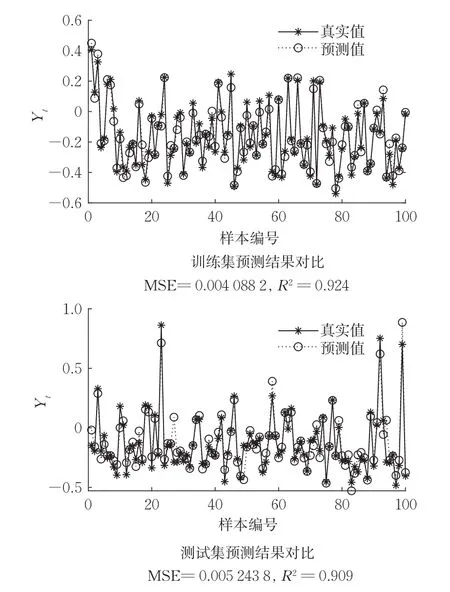
图5 算例5数值结果Fig.5 Numerical results of example 5
算例6parkinsons_updrs数据集预测
该数据集为由Athanasios Tsanas创建、Max Little与美国10个医疗中心、英特尔公司合作开发的远程监控设备所记录的语音信号。最初使用一系列线性和非线性回归方法预测临床医生在UPDRS量表上的帕金森病症状评分。共5875组数据,26个属性值,随机选取4000组作为训练集,其余1875组作为测试集。预测结果如图6所示,R2=0.983,非常接近于1,实验结果表明,属性值的增多并不会改变拟合效果。
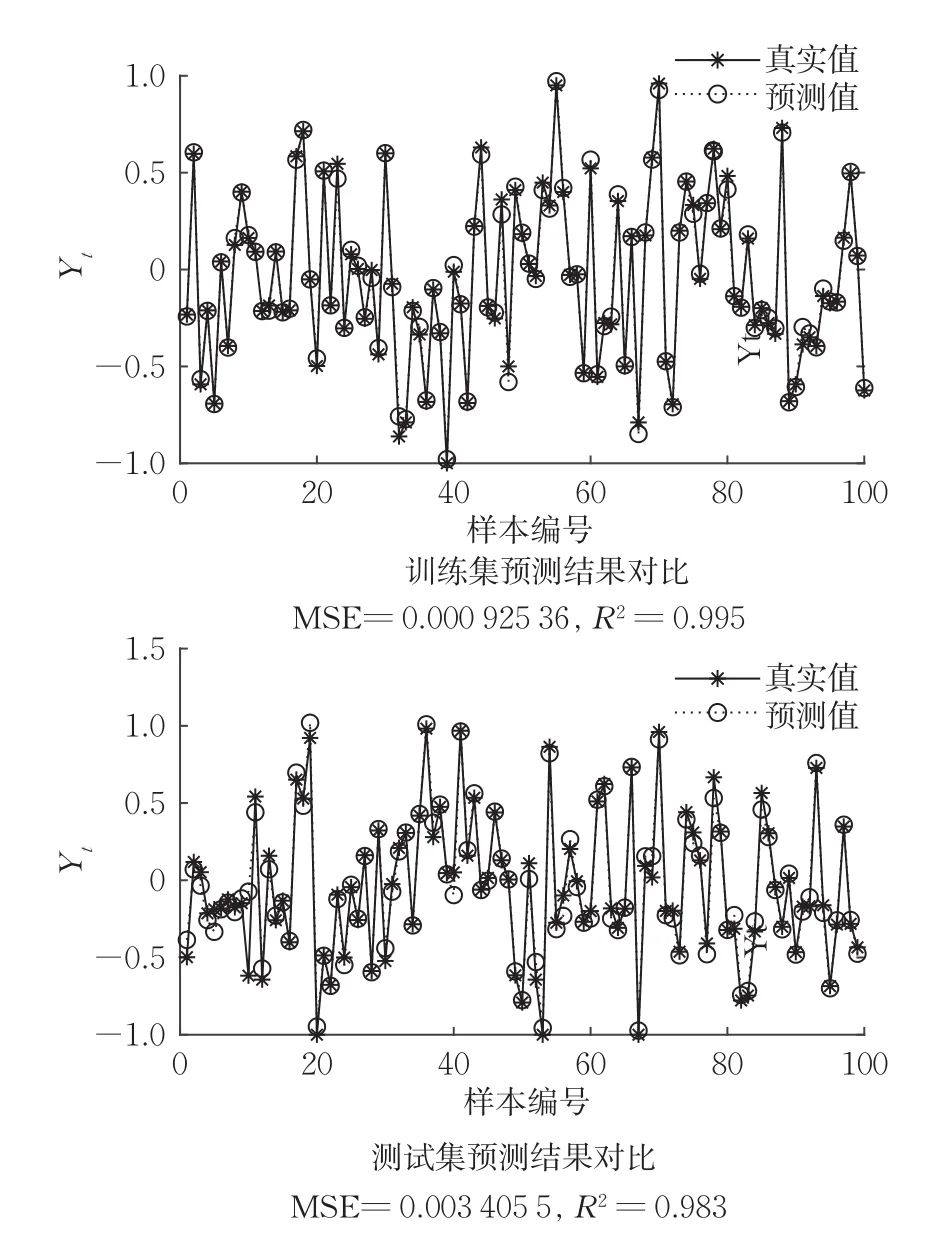
图6 算例6数值结果Fig.6 Numerical results of example 6
算例7SeoulBikeData数据集预测
目前,许多城市引入了共享单车,以提高出行的便捷性。能在合适的时间租到自行车,可减少公众的等待时间。此问题的关键是预测每小时所需的共享单车数。
数据集包含天气(温度、湿度、风速、能见度、露点、太阳辐射、降雪量、降雨量)、每小时共享单车租用数和日期等信息。共8700组数据,包含14个属性值。随机选取6000组作为训练集,其余2700组作为测试集。预测结果如图7所示,R2=0.860,拟合效果较好。结果表明,大规模数据具有较好拟合效果。
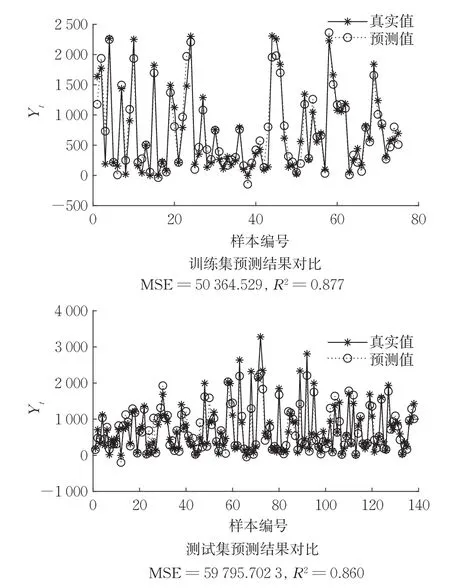
图7 算例7数值结果Fig.7 Numerical results of example 7
算例8kc_train数据集预测
数据集主要包括2014年5月至2015年5月美国King County的房屋销售价格以及房屋的基本信息。数据分为训练数据和测试数据两部分,分别保存在kc_train.csv和kc_test.csv两个文件中。其中训练数据主要包括10000条记录,14个字段,随机选取8000条作为训练集,其余2000条作为测试集。预测结果如图8所示,R2=0.790,非常接近0.8,拟合效果良好,可用于预测房价,结果再次表明,当数据量达到10000时拟合效果仍良好。
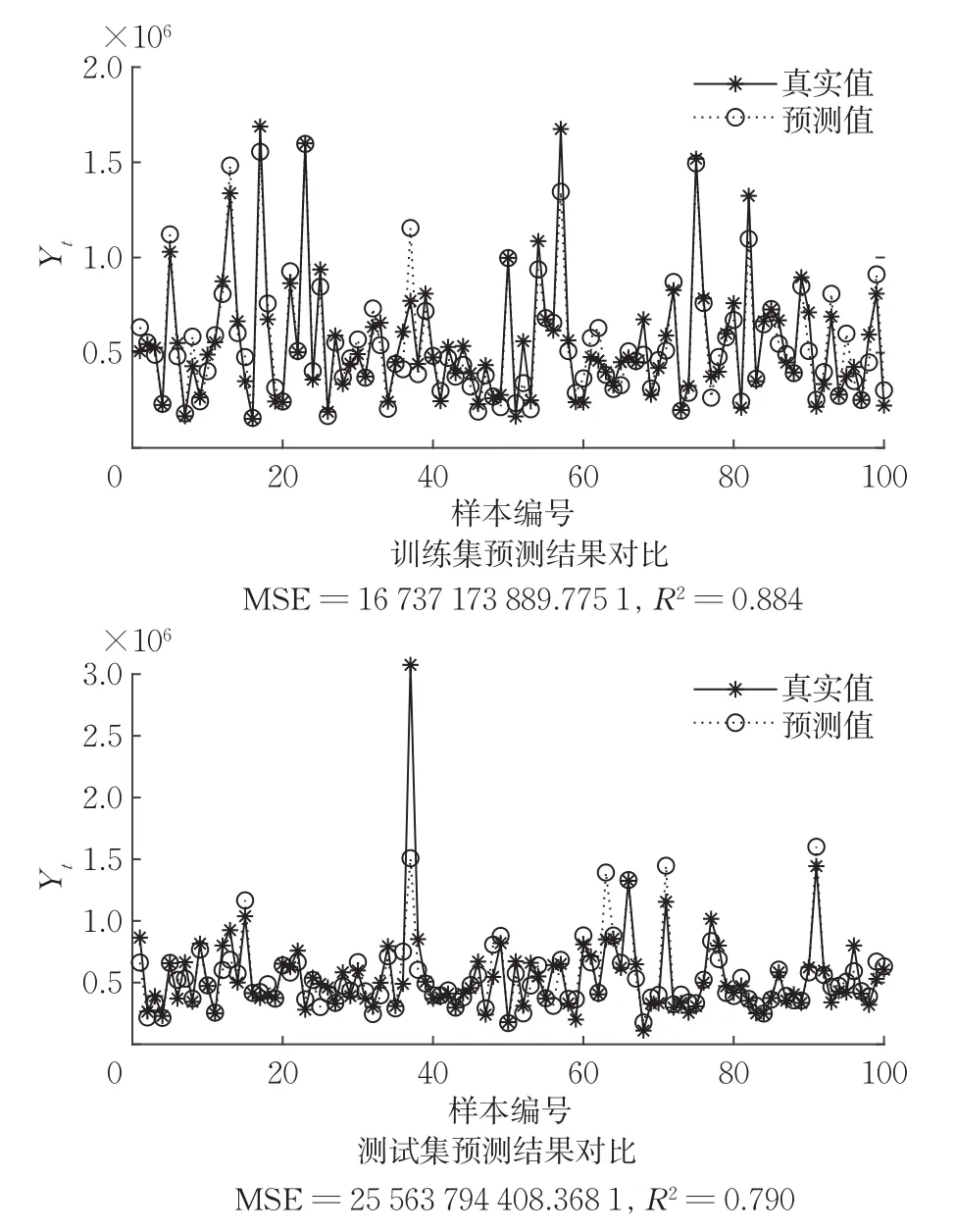
图8 算例8数值结果Fig.8 Numerical results of example 8
4 结 论
研究了如何用LS-SVM求解大规模矛盾方程组,并将其用于预测实际问题。在实验过程中不断修正参数值,使得训练模型更符合实际情况。通过对线性单变量和多变量问题、非线性单变量和多变量问题的研究,得到以下结论:
(1)数据类型,如线性与非线性、一元与多元并不影响数据的拟合度,对于不同类型的数据,只要找到适当的参数值,就可以得到具有良好效果的拟合模型,进行数据预测。
(2)从预测结果看,数据量的增多并不影响数据的拟合效果。

