基于曲边梯形面积刻画毕达哥拉斯模糊数的排序方法

陶玉杰，索春凤

(1.通化师范学院数学学院,吉林 通化 134002；2.北华大学数学与统计学院,吉林 吉林 132000)

0 引 言

自 1986年，ATANASSOV[1]首次提出直觉模糊集（intuitionistic fuzzy set，IFS）概念以来，IFS广受关注。特别是自CHEN等[2]提出得分函数和HONG等[3]提出精确函数后，IFS在多属性信息群体决策（MAGDM）领域得到迅猛发展。其主要原因是IFS在实际问题中能同时刻画支持、反对和中立3种态度，从而克服了传统模糊集仅由隶属度描述事物的局限性。然而，IFS也存在一定缺陷，例如，隶属度和非隶属度之和受小于等于1的限制，导致其无法处理某些实际信息，这对IFS理论的广泛应用提出了挑战。为此，2013年，YAGER 等[4]首次将 IFS的限制条件扩展为隶属度和非隶属度的平方之和小于等于1，拓展了IFS。此外，还提出了在毕达哥拉斯模糊环境下按等级的自然准则排序的规则，并用极坐标形式表示毕达哥拉斯模糊数（Pythagorean fuzzy number，PFN）[5]。近年来，国内外学者对 PFS 理论及其应用进行了广泛研究，尤其在决策分析方面取得了诸多成果，这些工作对进一步将PFN应用于多属性信息决策问题具有重要理论意义。

2014年，ZHANG等[6]采用隶属度和非隶属度平方差形式首次提出得分函数这一概念，但当得分函数相等时却出现了尴尬的局面。2015年，PENG等[7]针对文献[6]的不足，将隶属度和非隶属度平方和作为精确函数对其进行补充，但又面临新的问题：既然PFN是直觉模糊数（intuitionistic fuzzy number，IFN）的推广，那么PFN和IFN的排序结果是否存在矛盾？事实上，矛盾确实存在，例如，设α=(0.5，0.3)，β=(0.4，0.1)，若按文献[2-3]的方法，则其得分值S(α)=0.2＜0.3=S(β)，即α≺β，若按文献[6-7]的方法，则其得分值S(α)=0.52-0.32=0.16＞0.15=0.42-0.12=S(β)，即α≻β，矛盾。为此，出现了很多改进的得分函数[8-10]。然而，这些得分函数及其排序准则虽然克服了已有方法的一些缺陷，但亦带来了新的问题[11-12]。综合看，这些得分函数的构造主要基于代数方法，只对数学公式进行了改进，缺乏对其几何含义的考虑。

2017年，WAN 等[9]通过几何图形面积方法引入了知识测度（knowledge measure）和信息可靠性（information reliability）概念，并分别将知识测度和信息可靠性作为得分函数和精确函数，同时给出了PFNs的排序准则。遗憾的是，作者在推导信息可靠性（精确函数）时所用的三角形面积公式有错，造成精确函数的数学表达式出错，令给出的排序准则不可信。本文针对文献[9]所采用的几何方法，系统分析其在信息可靠性推导过程中出现错误的原因，并在毕达哥拉斯模糊环境下用曲边梯形面积（curved trapezoidal area，CTA）得到了新的得分函数，重新给出了PFN的排序准则，进一步通过与其他3种PFN排序方法对比，说明本文方法的优势。

1 基本定义

IFS作为传统模糊集的拓展，迅速成为决策分析中的主要研究工具。PFS不仅是IFS的推广，而且能在更广泛领域处理多属性模糊信息及其决策问题。两者的共同点是可分别采用隶属度、非隶属度和犹豫度刻画同意、反对和弃权3种态度，全面描述客观事物的模糊现象。

2 问题的提出

文献[9]推导信息可靠性Q(α)的几何示意见图1。

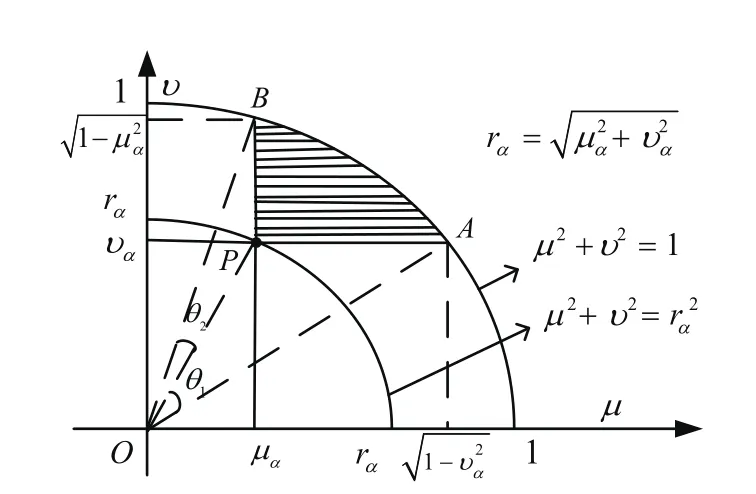
图1 文献[9]推导信息可靠性的几何示意Fig.1 Geometric diagram of information reliability derived from reference[9]

3 排序方法

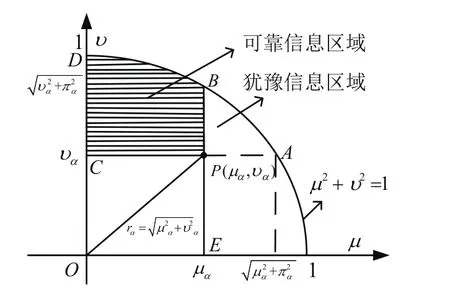
图2 PFNα的可靠信息区域和犹豫信息区域示意Fig.2 Geometric diagram of reliable information area and hesitant information area of PFNα

4 实例分析

为简单和直观起见，本文回避文献[9]而选择与文献[10-12]的方法进行比较。文献[10-12]所涉及的得分函数公式及其排序准则见表1。

表1 4种得分函数公式及其排序准则对比Table 1 Comparison of four ranking function formulas and their ranking criteria

由表1知，虽然经不断改进，得分函数公式有所不同，但排序准则相差不大，其中“～”指“等价于”，“≻”指“强于”。不难看出已有方法存在2个缺陷：不能进行精确比较；与传统IFN排序方法存在矛盾。

表2为4组PFNs下本文方法与文献[10-12]方法的比较，得分函数值根据表1公式计算得到。

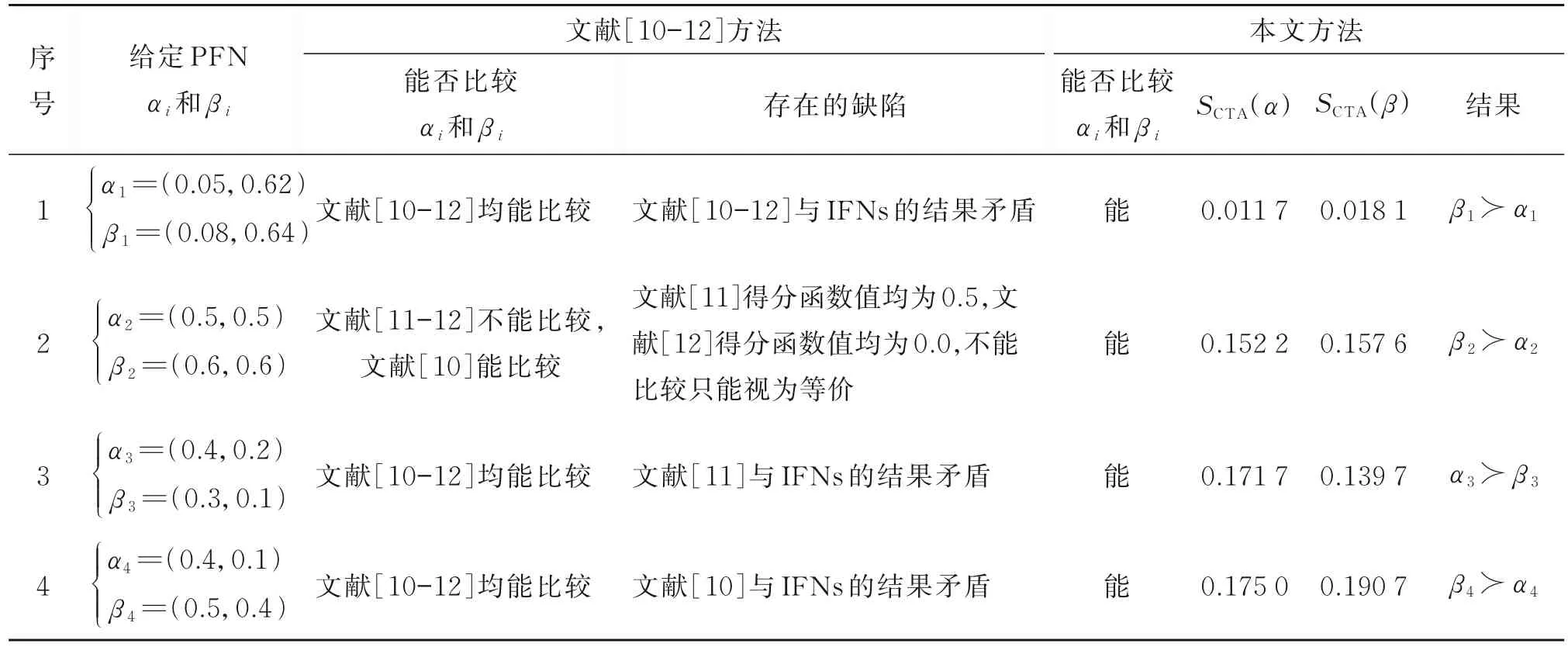
表2 本文方法与文献[10-12]方法的比较Table 2 Comparison of the proposed method and the methods in references[10-12]

从表2的4组PFN数据看，文献[10-12]方法均存在一定缺陷，原因是这些方法仅从得分函数式的代数意义上做改进，忽略了其几何意义。为进一步说明本文方法的优势，在毕达哥拉斯模糊环境下再选取3组PFN进行对比分析，见表3。

表3 本文方法与文献[10-12]方法排序对比Table 3 A comparison of the proposed method and the ranking method in references[10-12]

由表3知，文献[10-12]方法虽然克服了某些缺陷，但同时带来了新的问题。实际上，对α1=(0.7，0.5)和β1=(0.5，0.1)，按本文和文献[11-12]方法均得到β1≻α1，而按文献[10]方法却得到α1≻β1，说明文献[10]方法有缺陷，而本文方法具有合理性。对α2=(0.4，0.4)和β2=(0.6，0.6)，按文献[11-12]方法不能对其进行严格比较，只能视作α2～β2，而本文方法可以比较，且结果与文献[10]一致。说明文献[10-12]方法均在一定程度上存在缺陷，而本文方法克服了这些缺陷，所得结果与传统的IFN排序结果一致。

综上所述，本文方法的主要优势表现为：

（1）将所有PFN和IFN统一在第一象限单位圆内，提出了统一的得分函数及其排序方法；

（2）没有出现等价情况（α～β），实现对α与β的精确比较；

（3）没有出现与传统IFN排序不一致的情况；

（4）考虑了其几何含义，使方法更具一般性和科学性。

毋庸置疑，这些优势不仅克服了已有方法的某些缺陷，而且对进一步扩展PFN在决策分析中的应用具有重要理论意义。

5 结 论

PFS能有效、全面地处理一些具有不确定性和模糊性的问题，近年来被广泛应用于解决多属性指标信息的决策分析问题。通过PFN反映的可靠信息所对应的CTA提出了新的得分函数公式及其排序方法，并证明了方法的合理性。此外，通过选取几组PFN，与文献[10-12]方法进行了比较，结果说明本文方法不仅克服了文献[10-12]方法的某些缺陷，而且实现了将IFN和PFN统一排序的目标。然而，这些优势并不代表本文方法完美无缺，其仍存在其他缺陷，有待下一步重点研究。