立足学生 让数学学习走向深入
叶婷婷


【摘 要】立足学生,让教学围绕学生进行,就需要教师始终站在学生的立场,引领学生求本溯源,围绕知识的出发点,觅其根;巧设疑障,延伸知识,究其因;异中求同,体验价值,悟其真。在“分数的意义”的教学中,笔者不断引领学生深入学习,经历过程,逐步体会、感悟分数的意义。
【关键词】求本溯源 设疑障 抓核心
“分数的意义”是苏教版数学五年级下册的教学内容,理解单位“1”和分数单位的含义是这节课的重点,也是难点。单位“1”到底是什么?谁是单位“1”?为什么要用单位“1”?这是困扰很多学生的问题,也是教师在执教“分数的意义”时非常头疼的问题。在日常教学中笔者发现:学习这节课之前,学生已经对分数有了初步的认识,他们已经能非常熟练地表达——把“一块蛋糕”“一盘桃”等这样具体的对象平均分后得到一个具体的分数,通过这样的表述,基本都能清楚地表达他们自己的意思,此时硬“塞”给他们一个单位“1”,让他们把分的具体对象再重新描述,说成单位“1”,很多学生从心里是很难接受的,更不要说在学习中去主动地应用单位“1”。如何立足学生,从学生的视角出发,遵循他们的学情基础,直面他们在本节课学习中可能遇到的困惑?这就需要教师引领学生求本溯源,从学生已有的知识和经验出发,找到单位“1”的根;巧设疑障,在探索过程中深挖产生单位“1”的需要;异中求同,体悟概念的价值,让学生经历分数意义的抽象概括过程。为此,笔者在教学中进行了如下的思考与实践。
一、求本溯源,复习旧知有新意
“一个物体、一个计量单位或由许多物体组成的一个整体,都可以用自然数1来表示,通常我们把它叫作单位‘1’”,这是教材中对单位“1”的描述,乍一看是一段抽象生冷的文字,如何让这段文字变得鲜活起来,让学生亲切直观地体会这段文字呢?仔细阅读苏教版小学数学的12册教材会发现,这里的一个物体、一个计量单位、一个整体都是学生已经学习过或者接触过的:在三年级上册“分数的初步认识(一)”中,教材以蛋糕为对象进行平均分,这里的蛋糕就是一个物体;在三年级下册“分数的初步认识(二)”中,教材以一盘桃为对象进行平均分,这里的一盘桃就是一个整体;在三年级下册“小数的初步认识”中,教材以1米的直条为对象进行平均分,这里1米的直条就是一个计量单位。不仅如此,学生在之前的学习中,已经可以结合具体的对象用“把 平均分成 份,取其中的 份就是 ”这样规范的语言描述一个具体分数的含义,这段描述也正是本节课分数意义的学习基础。鉴于以上的思考,笔者在教学中唤醒学生对已有知识的思考,在回顾的基础上引导学生去对比发现,聚焦三要素——分的对象、分的方法、分的结果,在旧知的复习中让学生有新的理解、新的感悟,从而达到旧知出新意的效果。为此,笔者尝试了以下教学实践:
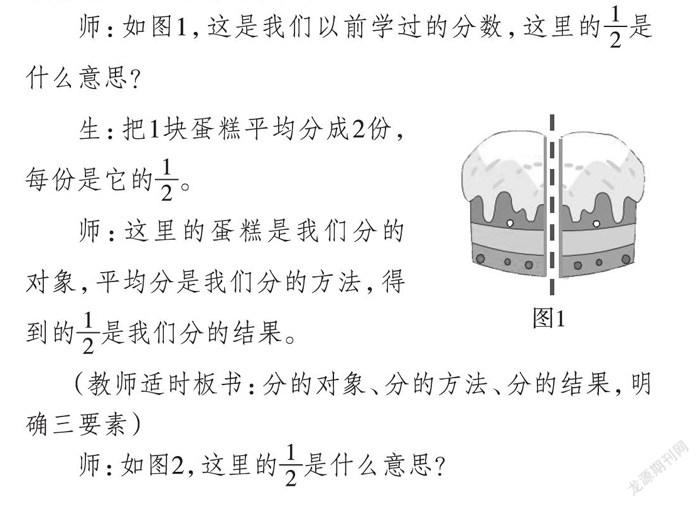
師:如图1,这是我们以前学过的分数,这里的1—2是什么意思?
生:把1块蛋糕平均分成2份,每份是它的1—2。
师:这里的蛋糕是我们分的对象,平均分是我们分的方法,得到的1—2是我们分的结果。
(教师适时板书:分的对象、分的方法、分的结果,明确三要素)
师:如图2,这里的1—2是什么意思?
师:(指三要素)你能分别说一说吗?
师:都是1—2,它们有什么不同?
(学生对比图1和图2,明确这里分的对象不同,蛋糕是一个物体、一盘桃是一个整体,教师适时板书:一个物体、一个整体)
师:如图3,这里的5—10是什么意思?
(出示三年级下册“小数的初步认识”)
生:把1米平均分成10份,取其中的5份就是5—10。
师:这里我们分的对象是(1米),1米也是一个计量单位。
(教师板书:计量单位)
师:比较这里的1—2和5—10,它们又有什么不同?
(屏幕出现图1、图2、图3)
师:同学们,这是我们学习过的有关分数的知识,它们分的对象既有像蛋糕这样的一个物体,也有像许多个桃子这样组成的一个整体,还有像1米这样的一个计量单位。所得的分数既可以表示这样的一份,也可以表示这样的几份。现在我们是五年级的学生了,再学分数会和以前有什么不一样呢?让我们一起开启今天的学习。
二、巧设疑障,学习新知有需要
通过第一环节的旧知回顾,学生可以用规范的数学语言完整地描述一个具体的分数的含义,同时在描述的过程中能抽离出“分的对象”“分的方法”和“分的结果”这三个要素,学生已有的知识积累为新知的探索奠定了非常好的基础。如何充分地利用这些已有的知识基础,为学生的进一步学习提供支架,在轻松愉悦的“我都会”中巧设疑障,让学生产生进一步学习的需要,笔者为此做了三点思考:一是利用小板贴将学生脑海中的分数画出来,以小组推荐的方式汇集不同学生心目中的分数,在对比交流中让学生思考这些分数的相同点和不同点,聚焦到分的对象有的是一个物体、有的是一个整体、有的是一个图形、有的是一个计量单位,利用学生的生成资源丰富单位“1”的内涵;二是引发学生对单位“1”的需要,在学生能规范表述一个分数的意义的基础上,从学生的作品中挑选出相同的分数(如1—2),请学生结合画的图说一说三要素,引发学生思考——都是1—2,为什么每个同学说的却不一样?将学生的目光聚焦到分的对象上,再进一步引发学生思考——你能用一句话概括1—2的含义吗?引发学生产生对单位“1”的需要;三是层层递进,在学生能用单位“1”描述一个具体的分数的基础上,尝试描述一类分数,最终建立分数的模型,完成分数意义的建构。具体教学过程如下:
师:首先我们一起来做一个活动。
活动要求:
①在板贴上写一个分数,画一画,表示它的意思。
②在小组里用三个要素说出它的意思。
③小组交流,推荐一幅作品贴在黑板上,准备全班交流。
师:你想画什么?
(学生在活动之前初步交流,教师适当引导以确保作品的丰富性,学生完成小组活动后将推荐的作品贴在黑板上)
师:仔细观察,你能将黑板上的作品分分类吗?
生1:可以根据分的对象分成4类。
生2:可以分成2类,表示其中的1份,表示其中的几份。
师:这些分类方法都是可以的,请大家仔细观察这些作品,如果老师随便挑一个,你们能用三要素说一说吗?自己准备一下。
【教师选择分数1—2,几个学生画的示意图却不同,呈现他们的作品(如图4),学生结合示意图说一说这里1—2的含义】
师:都是1—2,同样的分数,为什么大家说的不一样?
生:分的对象不一样。
师:你能用一句话概括1—2的意思吗?
小组讨论:
①怎么用一句话来表示1—2?
②你觉得最难解决的是什么?想一想怎样去解决。
生1:把分的对象平均分成2份,每份是它的1—2。
生2:把“1”平均分成2份,每份是它的1—2。
师:(追问)这里的“1”可以表示什么意思?
生:可以表示一个物体、一个图形、一个计量单位、一个整体。
师:真了不起,这个“1”可以把我们讲的所有的“1”都涵盖进来,这个“1”就是我们数学里讲的单位“1”,单位“1”就是我们分的对象。
师:用了单位“1”之后,和三年级学的分数在描述上相比,你感觉怎么样?
生:用单位“1”可以概括所有分的对象。
师:对于下面的分数,你能用单位“1”说一说吗?
1—4 3—5 —8 1— —
三、巧抓核心,理解概念有体悟
学生建构了分数意义的概念后,建构分数单位的概念似乎是水到渠成的事,很多教师在教学中往往也是一带而过。诚然,教师在建构分数意义之后直接给出分数单位的概念,学生接受起来也很顺利,但是,为什么要有分数单位的概念?分数单位又有什么价值?为什么表示其中的1份就是分数单位,而不是2份、3份?学生看似知道了分数单位的意思,但其实对于概念背后的问题并不清楚,呈现出的是似懂非懂的状态。如何让学生在众多的分数中自然地关注到分数单位,并且感受到其他的分数都和它有着密切的关系,笔者为此又设计了下面的活动环节:
分一分、涂一涂,用阴影表示你想表示的分数。
生:1—5、2—5、3—5、4—5。
师:这4个分数为什么分母相同,分子不同?
生:平均分的份数相同,取的份数不同。
师:(追问)你觉得这4个分数中哪一个是最核心的分数?
生:1—5,因为其他的分数都可以看成由几个1—5组成。
师:把单位“1”平均分成若干份,我们把其中表示1份的数叫作分數单位。
师:(追问)4—5的分数单位是多少?3—5呢?1—5呢?
本节课,笔者不断引领学生探寻分数的意义,注重让学习经历循序渐进的“慢”过程,引领学生从表象走向深入。纵观整节课的教学设计,立足学生,从学生的知识基础出发,做到以生而为;巧设疑障,让学生产生进一步学习的需要,激发学习活动的发生;巧抓核心,让学生体悟概念的价值,让学生的学习逐步走向深入。

