MATLAB在线性时不变系统时域求解中的应用

安成锦，杨俊刚，王雪莹，吴 京

（国防科技大学电子科学学院，湖南 长沙 410073）

0 引言

系统的时域分析是指在给定的激励作用下，通过不同的数学方法求解系统的响应。为了确定线性时不变系统对给定激励的响应，需要建立描述该系统的方程，并给出一定的初始状态。如果把对系统的定性和定量分析限定在时域内，这就是系统的时域分析法[1]。

利用手工求解方程，尤其是高阶方程有一定的难度。将MATLAB引入到信号与系统分析中，把常用的求解方法编写成MATLAB代码，供求解实际问题时直接使用。既可以避免烦琐的数学运算，简化问题的求解过程，又可以实现分析结果的可视化[2]。

但目前“信号与系统”方面的书籍，要么没有介绍系统求解的MATLAB实现[3][4]，要么仅介绍了零输入响应求解，缺少完整的连续、离散系统的零输入、零状态响应MATLAB求解方法[5][6]。本文首先介绍了利用MATLAB从时域求解连续系统的方法，接着介绍了求解离散系统的方法，最后对结果进行了一定的分析。

1 连续时间线性时不变系统零状态响应求解实例

连续时间系统的数值求解在MATLAB中可利用控制系统工具箱中的lsim函数，调用形式为：

lsim(sys,u,t,x0)

其中sys是系统的表示，向量u和t分别表示输入信号和时间t的抽样值，向量x0表示系统的初始状态，缺省值为0，返回值为系统的输出。如果调用lsim(sys,u,t)，得到的结果即为系统的零状态响应。

解：MATLAB源代码如下，程序运行结果如图1所示。

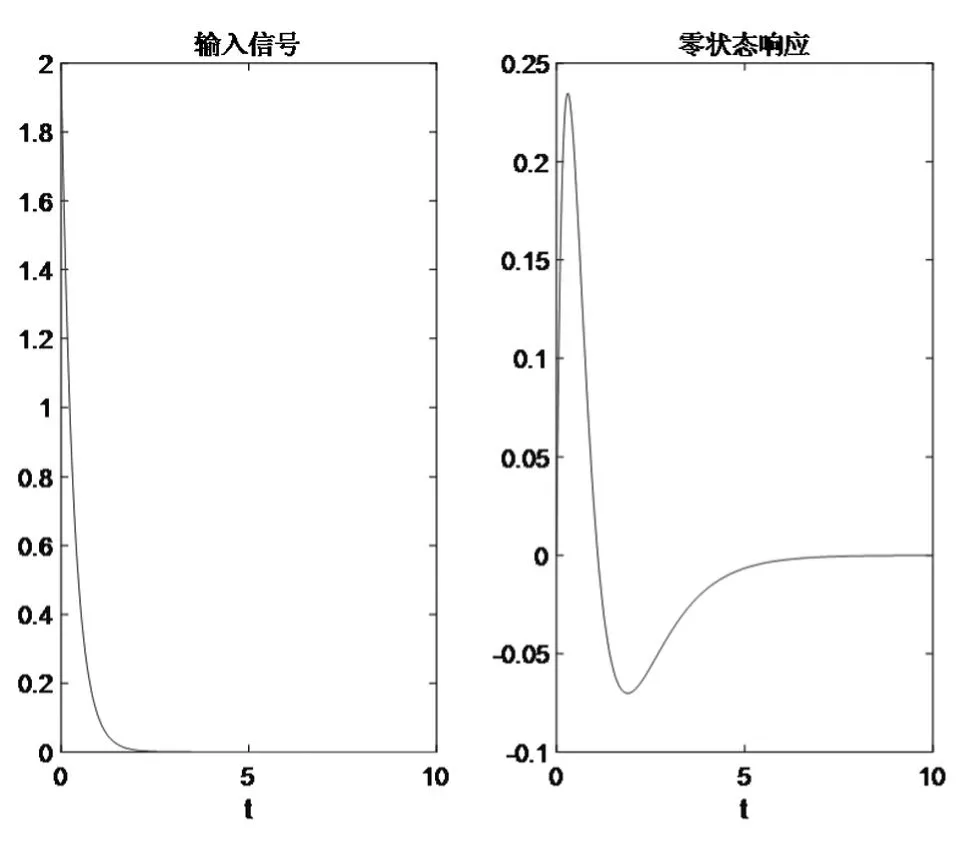
图1 连续时间系统的零状态响应

2 连续时间线性时不变系统零输入响应求解实例

通常认为将lsim函数的输入信号置零，再将初始状态代入x0，则可得到连续时间系统的零输入响应。但事实上lsim函数只能对状态方程描述的系统计算零输入响应，对前面得到的输入-输出系统的表示失效[7]。虽然在MATLAB中没有专门的函数求解连续时间系统零输入响应的数值解，但可利用dsolve函数得出解析解。调用形式为：

S=dsolve(eqn,cond)

其中eqn为方程，cond为初始条件。

解：MATLAB源代码如下，程序运行结果如图2所示。

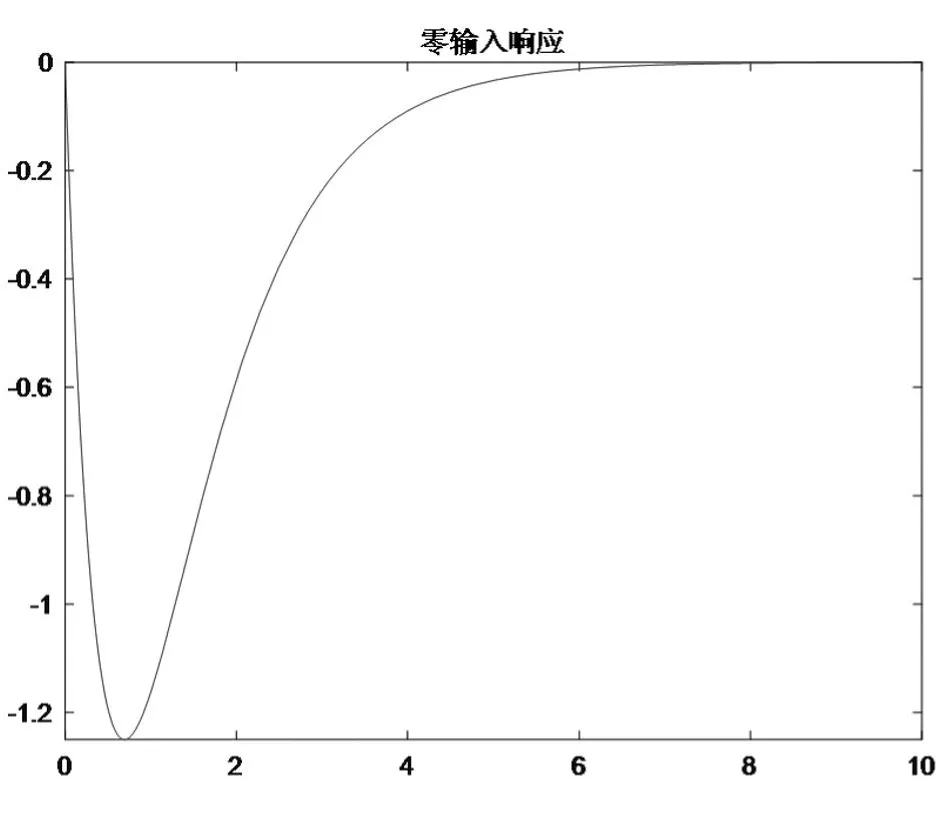
图2 连续时间系统的零输入响应

3 离散时间线性时不变系统零状态响应求解实例

大部分离散时间线性时不变系统可以用常系数线性差分方程表示：

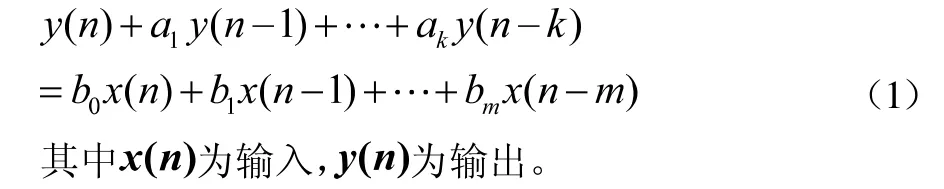
离散时间系统的数值求解在MATLAB中可利用信号处理工具箱中的filter函数，调用形式为：

y=filter(b,a,x,zi)

解：MATLAB源代码如下，程序运行结果如3所示。观察发现，输入有界时，零状态响应发散，该系统为不稳定系统。

图3 离散时间系统的零状态响应

4 离散时间线性时不变系统零输入响应求解实例

通常认为将filter函数的输入信号置零，再将初始状态代入x0，则可得到离散时间系统的零输入响应。但与连续时间系统的lsim函数类似，filter函数只能对状态方程描述的系统计算计算零输入响应。在MATLAB中，有专门的函数将初始状态由传递函数描述的系统转换成状态方程描述的系统，调用形式为：

z=filtic(b,a,y,x)

其中b、a还是输入、输出信号的系数向量；y表示输出；x表示输入，缺省值为0；z表示状态方程的初始状态。

得到z后，再将其代入filter函数，并令输入为零，即可得到系统的零输入响应。

解：MATLAB源代码如下，程序运行结果如图4所示。

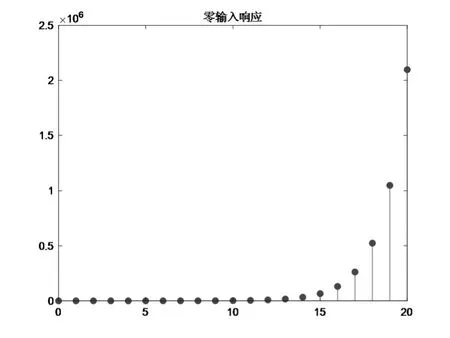
图4 离散时间系统的零输入响应

5 离散时间线性时不变系统全响应求解实例

对于离散时间系统全响应求解，可以利用filter函数，代入输入序列和初始状态直接得出；也可以将差分方程进行一定的整理，将输出y(n)单独放在等号一边，对于例4，即为，然后编程迭代得到。

解：MATLAB源代码如下，程序运行结果如图5所示，比较发现两种方法得到的全响应相等。

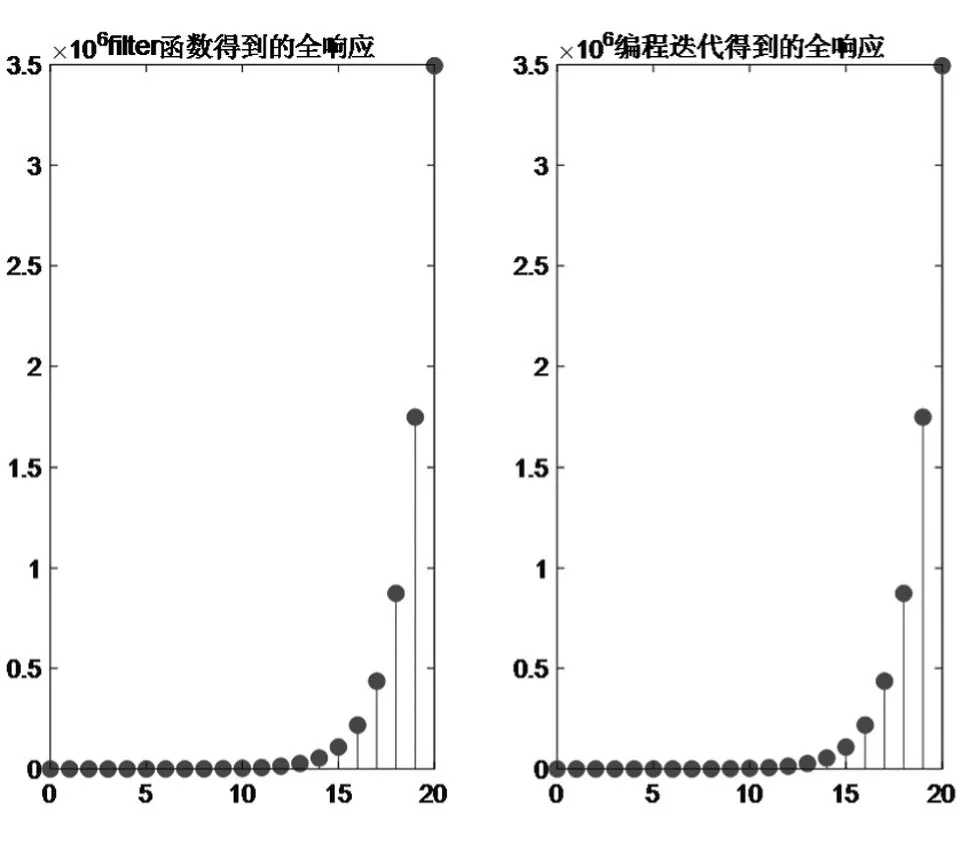
图5 两种方法得到的离散时间系统全响应

6 结语

结果表明，MATLAB的数值计算和符号计算功能可使线性时不变系统的响应求解过程大大简化，并能得到可视化效果。文章涉及的是系统时域求解问题，事实上，MATLAB在频域、复频域、Z域分析和求解中也得到了广泛的运用。