具有时变全状态约束的非线性随机切换系统的自适应神经网络控制

李 争，刘 磊，刘艳军

（辽宁工业大学 理学院，辽宁 锦州 121001）

切换系统是由一系列的连续或离散的子系统以及协调这些子系统之间的切换规则组成的系统。在实际的生产活动中，许多控制系统常常同时含有连续时间动态和离散时间动态，而切换系统作为一种典型的混杂系统解决了许多相应的实际问题，如无人机[1]、互联网流量分类[2]、永磁磁通切换电机[3]等。并且，与非切换系统的稳定性不同，切换系统不能直接继承子系统的稳定性。由于切换系统独特的稳定性特性，切换系统的稳定性问题一直是广受关注的重点内容。研究人员在对切换系统进行控制研究时，系统稳定性是亟需攻克的一大难关。目前，有关于切换系统的稳定性问题可以大致分为如下几种：切换系统在任意切换下的稳定性条件[4-6]、切换系统在受限条件下的稳定性问题[7-8]以及构造切换信号使得切换系统达到稳定[9-10]。除此之外，对切换系统进行稳定性分析的方法主要有：共同Lyapunov函数方法、单Lyapunov函数方法以及多Lyapunov函数方法。值得注意的是，关于非线性切换系统的研究尚处于起步阶段。虽然近几年涌现了很多优秀的研究成果[11-12]，但是由于实际生产活动中存在各种限制以及非线性本身固有的复杂性，为了提高控制品质，关于非线性切换系统的约束控制研究面临了很大的挑战性。

随着实际工程的发展，控制系统在工作时会受到各种限制。当系统违反这些限制而强行工作时，可能会给实际的生产活动带来巨大的财产损失，甚至威胁到生命安全。因此，在进行控制问题研究时，必须将系统的约束问题放在首要地位[13]。尤其在非线性切换系统的控制研究中，为了使所设计的控制策略更好地解决实际问题，就必须考虑其约束控制问题。现有的约束控制研究成果主要涉及到两种类型：常数型约束[14]和时变型约束[15-16]。时变型约束条件随着时间的变化发生改变，控制算法的设计比常数型约束要更为复杂，设计出的控制方案更具实用性，为生产活动提供更为坚实的安全保障。在某种意义上来说，常数型约束也可以看成是特殊的时变型约束。目前，障碍Lyapunov函数是解决控制系统约束问题的一个十分有效的工具，常见的形式主要有以下几种：对数型[17]、正切型[18]和积分型[19]。然而，除了约束控制问题外，随机特征也常存在于实际系统中，是影响非线性系统稳定性的一个重要因素。因此，在对非线性切换系统进行研究时，随机特征也是需要考虑的一个重要因素。

20世纪中期，为了提高系统的运行性能，保证系统的稳定性，随机稳定性的定义首次被提出[20]。之后，一些经典的随机稳定性理论，如随机拉萨尔不变性原理[21]和随机输入−状态稳定(Stochastic Input-to-State Stable)[22]等也相继被提出。在过去的几十年中，随机非线性系统的控制得到了突飞猛进的发展[23-24]。在研究过程中，为了补偿随机特征带来的不利影响，引入了ItÔ随机微分方程。与此同时，由于实际系统中常存在不确定性，采用精确的模型描述实际系统具有局限性。为了获得更好的控制效果，神经网络[25-26]和模糊逻辑系统[27-28]成为处理系统不确定性的重要工具，解决了很多控制难题。之后，有学者针对不确定非线性随机切换系统进行研究，涌现了很多成果，如不确定非线性随机切换系统的跟踪控制[11-12]，不确定非线性随机切换系统的常数型输出约束控制[29]以及不确定非线性随机切换系统的常数型全状态约束控制[30]等。但是，上述成果未对不确定非线性随机切换系统进行时变型全状态约束控制研究。

基于上述成果的启发，为了消除随机因素对系统控制性能带来的不利影响和增强控制策略的实际应用价值，本文以不确定非线性随机切换系统为研究对象，采用神经网络处理系统中的不确定项，研究了其时变型全状态约束控制问题。基于任意切换规则，通过坐标变换技术，实现了对系统所有状态的时变型约束控制。最后，借助随机李雅普诺夫稳定性理论，实现系统稳定性分析。本文所做的主要贡献如下：

(1) 对不确定非线性随机切换系统进行全状态约束控制研究，要求被控系统的所有状态均不违反约束，控制要求更高，控制难度增大。

(2) 对系统状态采用的约束类型为时变型约束。在设计控制策略的过程中，约束条件将随着时间的改变而发生变化，控制算法更难，设计的控制方案更具有实用性。

(3) 与之前采用障碍李雅普诺夫函数解决系统状态约束问题不同，本文采用坐标变换方法，实现对系统状态的时变型约束，设计方法新颖，且能够更好地保证系统的稳定性问题。

1 系统描述和控制目标

2 系统变换和预备知识

为了解决系统(1)的状态约束问题，引入非线性坐标变换

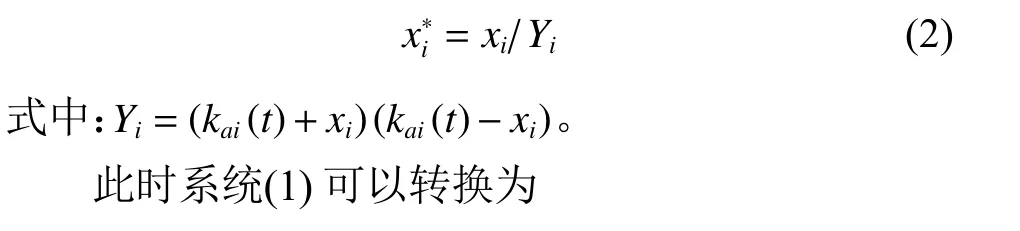
3 控制器设计与稳定性分析

本节借助backstepping控制算法，针对不确定非线性随机切换系统设计一种自适应神经网络控制策略，保证系统的所有状态均不违反时变约束。

首先为了设计控制策略，本文引入如式(11)所示坐标变换。

4 仿真研究

在这一部分，将提供一个数值仿真，验证设计的控制策略对具有全状态时变约束的不确定非线性随机切换系统的有效性。

例1 考虑如下不确定非线性随机切换系统：

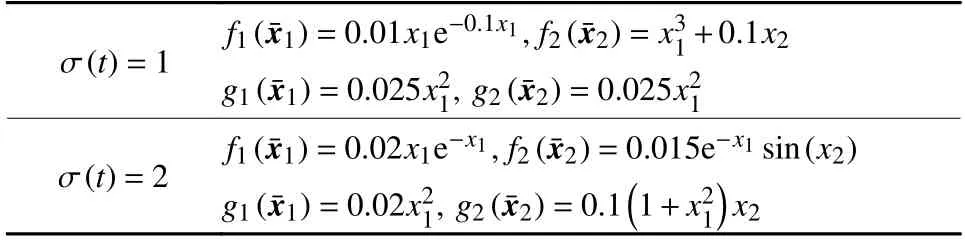
表1 系统(59)中的部分函数Table 1 Partial functions in system (59)

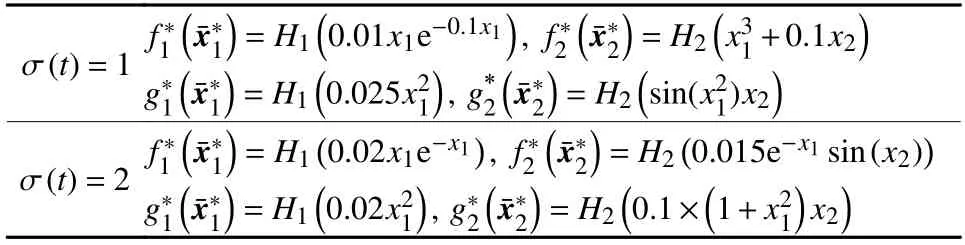
表2 系统(60)中的部分函数Table 2 Partial functions in system (60)

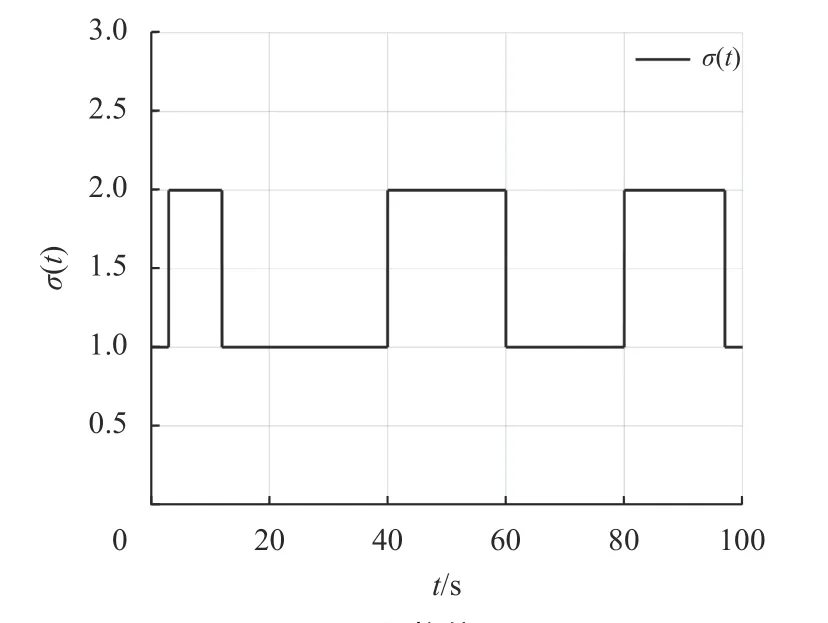
图1 切换信号Fig.1 Switching signal

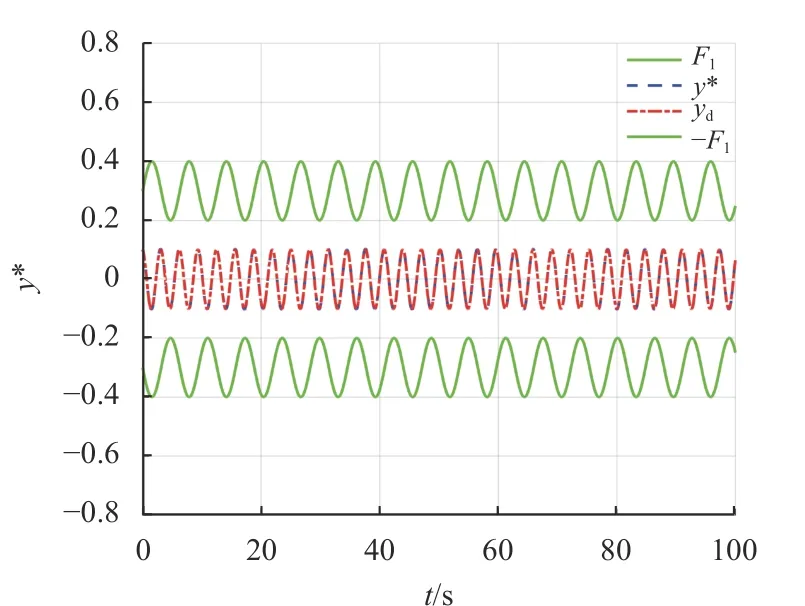
图2 系统输出、跟踪信号和约束条件Fig.2 System output, tracking signal and constraints

图3 系统状态和约束条件Fig.3 System state and constraints

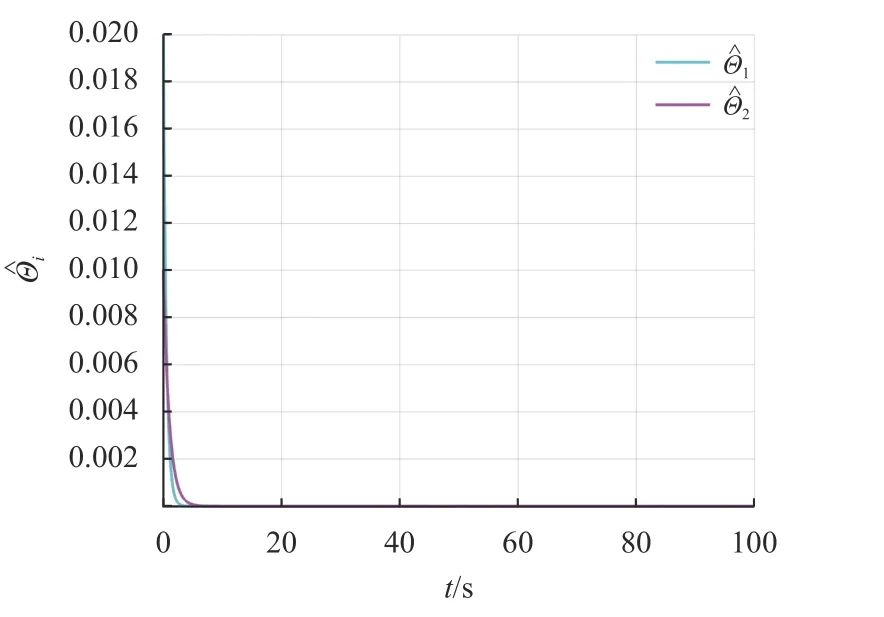
图4 自适应律轨迹Fig.4 The trajectories of adaptive laws

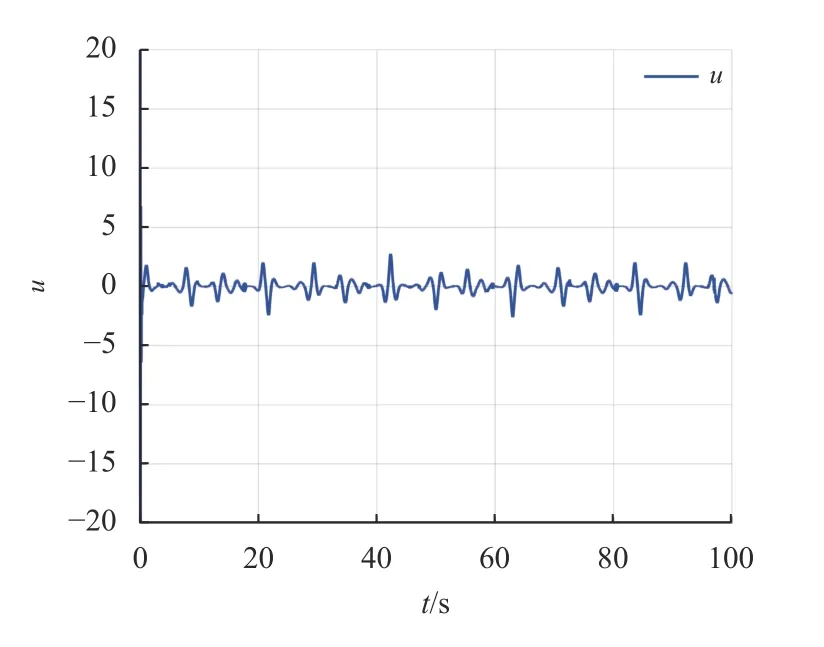
图5 控制器轨迹Fig.5 The trajectory of controller

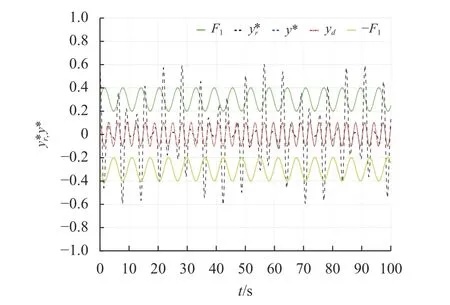
图6 本文输出，[29]中的输出，跟踪信号和约束条件Fig.6 System output in this paper, system output in [29], tracking signal and constraints

5 结论

本文针对一类不确定非线性随机切换系统进行了全状态约束控制研究，基于任意切换规则，设计了一种自适应神经网络控制策略。所针对的约束类型为时变型约束，约束条件将随着时间而发生改变，在设计控制方案的过程中涉及到的控制算法较复杂。除此之外，本文采用了坐标变换技术来解决系统的状态约束问题，方法新颖且更好地解决了系统状态约束问题。最后，通过数值仿真实验可知本文所设计的控制策略能够达到较好的控制效果。