一种考虑多能源互补的电力系统经济调度方法

杨金洲

（华北电力大学 电气与电子工程学院，北京 102206）

0 引 言

我国在2020年联合国大会上明确指出要在2030年前达到碳排放峰值，即“碳达峰”，并努力争取2060年前实现“碳中和”。太阳能、风能以及地热能等可再生新能源由于其污染小、可持续等特点，正逐渐取代化石能源等一次能源的主体地位。然而风光能源本身的波动性与不确定性会在一定程度上威胁局部电网的稳定性，从而对系统运行的调度与操作灵活性提出了更高的要求。为了减少新能源机组并网后短时的电压波动，电力系统在频率控制、电压调节、备用容量以及无功补偿等方面的设备投资成本增加，此外可再生能源远距离输电还会造成线损增加，电网的经济性被削弱。

为解决新能源并网消纳和配电网经济运行之间的矛盾，提出了多能源电力系统经济调度的方法。同时考虑了配电网、环境以及负荷侧三方效益，用主从博弈模型得出最优解。用多胞体法量化了系统灵活性，建立起满足灵活性需求空间分布约束的优化滚动调度模型求解。从宏观角度考虑了政策扶持、技术进步对电网运行成本的影响[1-3]。

1 新能源电力系统经济调度方法分析

1.1 优化调度的基本角度

1.2 多能源互补协调优化的优势

多能源互补协调优化的优势在于以下几点。第一，能够提高能源的发电效率。在资源丰富的非负荷中心建立水光风储互补电站，可以最大程度地外送电能。因为储能可以减少电力波动、削峰填谷，水力发电具有很高的灵活性，可作为备用机组，所以多能互补的发电形式可以弥补各个能源的不足、提高新能源的消纳、创造更多的经济效益。第二，促进了能源结构转型。新能源消纳能力增强会进一步推动清洁能源的发展。第三，加快了智能能源体系的建设。此外，互联网技术也会推进多能互补的应用范围扩大。

1.3 优化方案

多能源互补电力系统创新性地利用了物理层和信息层技术，将常规燃煤煤电、燃气发电、风电、光伏发电等多种可再生能源与大电网整合在一起，以实现各个能源系统间的协调、规划、运行、管理以及补充。考虑到不同能源与复合的对应关系。多能源电力系统的发电出力端如图1所示。

图1 多能源电力系统的发电出力端

2 多能源电力系统分析

2.1 出力端能源特性分析

2.1.1 燃气发电站

郭林等人提出了一种综合考虑储热和电锅炉协同运行的新能源消纳潜力分析模型，主要利用了堆栈去噪自编码器（Stacked Denoised Autoencoder，SDAE）深度神经网络预测的天然气管道流量方程线性化方法，并基于此线性模型构建了电-气综合能源系统经济调度先行优化模型，最后构建了完善的指标体系来定量评估储热和电锅炉对系统弃风与弃光的改善作用[4]。该模型解决了电力网络、天然气网络以及热力网络中潮流方程非线性化程度高的难点，并考虑了综合能源系统对新能源消纳的影响，对综合能源系统的经济调度有很大的借鉴意义。

2.1.2 光伏发电站

由一般硅光电池的电流、照度以及温度关系可得：

式中：U为节电压；I0为二极管反向饱和电流；Iph为与光照强度成正比的光生电流，且与负载等效电阻大小和电池的结构与材料有关；n为理想系数为常数；q为电子电荷；kB为波尔茨曼常数；T为绝对温度。

将U和I与光照强度、温度的关系分别取常见值在Simulink中进行仿真，结果如图2、图3所示。可以看出，无论是在不同温度下或者不同光照强度下，在电压不太高的情况下电流都可以保持约为常值，发电出力能够保持一定的相对线性度。

该项目使用的黑水角阀的阀套与阀芯采用机械紧固连接。由于黑水的高速冲击或流量大范围波动，连接处易出现松动，引起阀芯的震动；而阀芯材质为整体烧结硬质合金，硬度高，脆性大，在该频繁振动的工况下容易出现阀芯震裂、震碎与阀套脱离现象，使阀门失去调节作用。

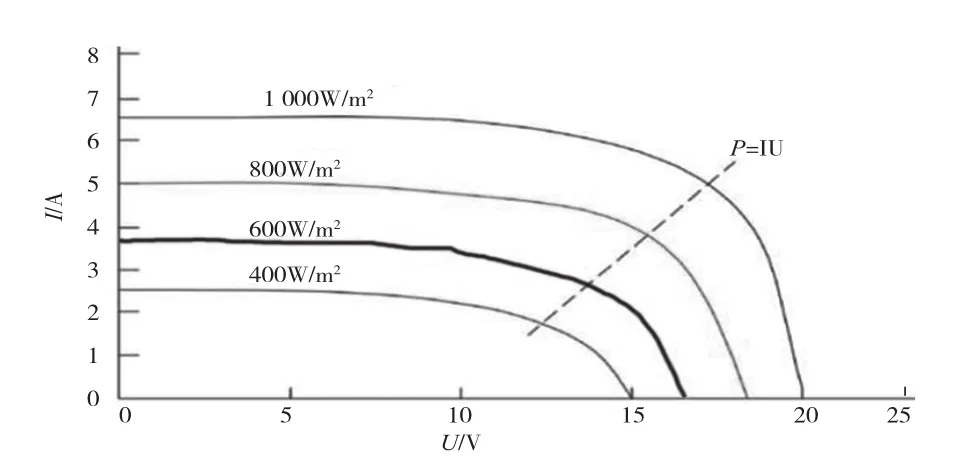
图2 不同光照强度下光伏电池的U-I特性曲线（T=25 ℃）

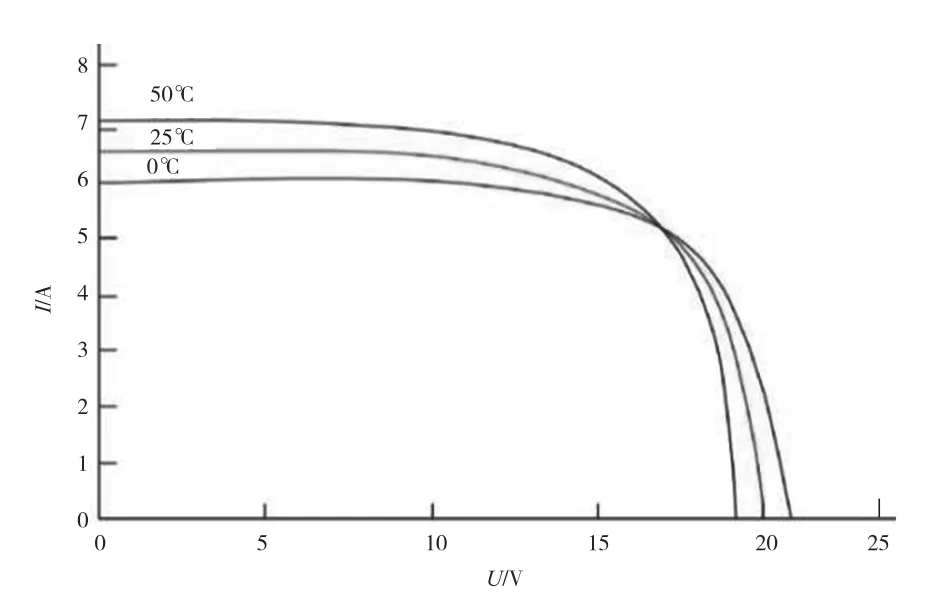
图3 不同温度下光伏电池的U-I特性曲线（S=800 W/m2）

2.1.3 风力发电站

风力机输出功率随着转速的变化而变化，存在一个最佳的转速。当处于最佳转速时，输出功率与风速的关系是最佳叶尖速比。在风速变化时可对机组转速进行调节，使其维持在最佳叶尖速比处，实现线性化控制。

2.1.4 抽水蓄能电站

抽水蓄能电站的优势在于其可作发电、蓄能两用，在用电低谷抽水蓄能，在用电高峰开闸放水发电，并且机组启动迅速，具有较高的灵活性。一方面弥补了常规发电机组启停时间长的缺点，解决了新能源发电机组出力波动大的问题，增强了系统的稳定性；另一方面民用抽水蓄能电站可以借阻塞盈余产生经济效益，缺点是对地理条件和场地要求较高，建设和维护成本巨大。总体而言，抽水蓄能电站循环寿命长、综合运行成本较低，能够在较大程度上保持系统各机组出力的相对线性[5]。

2.1.5 储能装置

在风光电渗透率超过50%的情况下（尤其是风电），反映区域振荡模态的特征根变为正根，新能源电力系统中需配置相应的储能装置，保障电网稳定运行、改善电能质量[6]。现有的储能技术可分为机械储能、电磁储能以及化学储能，其中电磁储能包含超导储能和电容储能，特点是能量密度低、响应速度快。化学储能主要通过铅酸电池、Na2S电池和液流电池等，储能成本低，但寿命短、污染大，相比之下抽水蓄能电站虽然一次投资大，但可长期使用且对环境友好，可在地理条件允许情况下大规模建设，在负荷预测与负荷调节环节中具有重要地位。

2.2 能源互补效果分析

常规煤气能源的灵活性恰好弥补了风能和太阳能时间尺度上显著的随机性与间歇性，同时风光之间又能在一定程度上弥补互相之间的发电不稳定性。对风光互补系统的出力进行评估和规划可以提高新能源并网消纳率，从而提高电网环境效益。杨晓萍等人采用随机模拟技术和改进粒子群算法相结合的方法求解了基于随机规划的风光互补系统准入极限，并考虑了不同季节对功率极限的影响。针对离散变量的约束优化问题，粒子群算法过程简单、易于理解，广泛应用于系统的最优调度问题的求解，但标准粒子群算法早熟、收敛速度慢、易陷入局部最优，故常采用调整学习因子和惯性权重的优化粒子群算法来求解[7]。

3 多能源互补联合发电机组组合优化调度模型

3.1 应用于机组组合的混合整数线性规划

以上的动态规划法只适用于小微电网，为了应用于机组数量较多的电力系统的经济调度可将其扩展并分段线性化处理，提出一种专门应用于多能源互补安全约束机组组合（Security-Constrained Unit Commitment，SCUC）的混合整数线性规划优化数学模型。

3.1.1 目标函数

基于混合整数线性规划的多时段电力系统经济调度的机组优化数学模型的目标函数为：

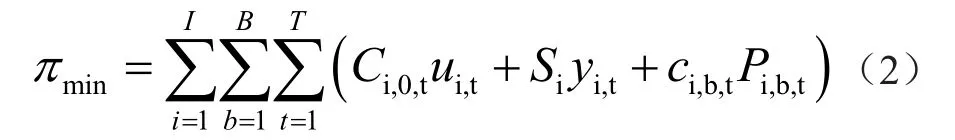
式中：i为机组索引；b为分段索引；t为时段索引；I为机组总台数；B为分段数；T为时段数；Ci,0,t为机组i第t时段最小出力的成本；Pi,b,t为机组i第b段第t时段的输出功率，为待优化的变量；Ci,b,t表示机组i第b段第t时段的边际成本；Si表示机组i启动成本。ui,t表示机组i第t时段运行状态，为待优化的{0,1}二进制变量；yi,t表示机组i第t时段启动状态，也为待优化的{0,1}二进制变量。

3.1.2 约束条件

（1）机组出力约束条件为：

式中：Pi,t表示机组i第t时段输出功率，为待优化变量；Pmin,i,t表示机组i第t时段最小输出功率；Dt表示第t时段负荷；Pmax,i,b,t表示机组i第b段第t时段的功率上限。

（2）机组爬坡约束条件与热备用约束条件为：

式中：Pup,t与Pdown,t分别表示机组i第t时段的上、下爬坡率；Pmax,i,t表示机组i第t时段的最大输出功率；Ht为系统热备用要求。此时应注意，风光发电出力相对于燃气发电出力几乎不可调。

（3）机组状态约束条件为：

式中：Zi,t表示机组i第t时段停机状态变量，为待优化的{0,1}二进制变量。

（4）运行与停运约束条件为：

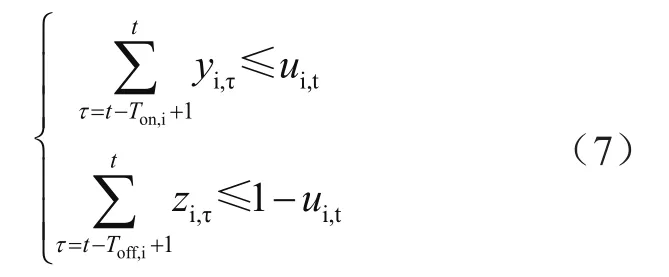
式中：Ton,i表示机组i最小运行时间；Toff,i表示机组i最小停运时间。

（5）潮流约束条件为：

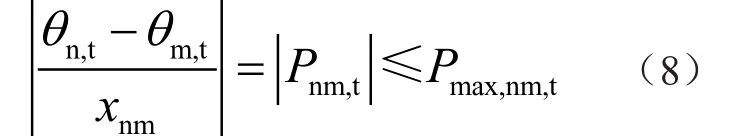
式中：θn,t表示节点n第t时段相角，为待优化变量；Pmax,nm,t表示线路nm第t时段潮流上限。

3.2 多能源互补电力系统机组组合经济调度的评价

基于协调煤、气、风、光分段线性出力的多能源互补经济调度可以在满足系统中各种功能需求的同时，提升能源的利用效率，是未来能源结构改革的主要方向。但综合能源系统的经济调度必须考虑各个能源的调度特性和地区差异，在运算方法上也要解决潮流方程非线性化程度高的问题，秉持安全、经济以及可持续的原则，对调度模型进行进一步的优化。

4 结 论

新能源发电未来会进一步与传统煤、气能源发电有机结合且在多能源电力系统中的占比稳步上升，直至使整个系统发挥最大的经济效益和环境效益。每种能源自身的特性决定了它们相互之间相辅相成、缺一不可的关系，但如何把握多能源的经济调度和改进新能源发电性能是当下亟待解决的问题。未来应更注重新能源消纳潜力的发掘，只有从根本上提高新能源消纳潜力，才能在系统中发挥新能源发电的优势，促进多能源系统的长期发展。