基于启发式强化学习的移动机器人路径规划算法研究
潘国倩,周新志
(四川大学电子信息学院,成都 610065)
0 引言
路径规划是移动机器人完成各种任务的必要前提,也是其进入现实生活的重要环节,还是研究智能机器人的重要组成部分,其主要目的就是要在机器人的运行环境中找到一条从起点到终点的无碰撞路径。根据机器人对环境的已知程度,目前的路径规划方法可以分为环境已知的全局路径规划和环境未知的局部路径规划,如人工势场法、模糊逻辑算法、蚁群算法、粒子群算法、神经网络算法等。由于移动机器人在实际应用中需要应对一些突发情况,因此有必要引入一种自学习的机制使得机器人能够通过学习来实现自主避障。
强化学习是一种基于“试错”方式的学习算法,机器人通过不断尝试动作来与环境进行交互,获得环境反馈的“奖励”,进而选择最佳动作规划路径。其不仅通过结合神经网络、智能控制及运筹学等算法或理论知识在理论和应用方面发展迅速,而且也被越来越多地运用在机器人的自动控制、运动以及智能调度等领域,在人工智能方面成为了学者们研究的热点。其中,Q-learning算法是目前使用最为广泛的强化学习算法。Q-learning算法被应用于机器人路径规划时,由于其不具先验知识,一般会直接将Q值表初始化为全零的矩阵,故往往存在学习时间长、收敛速度慢等问题。目前,已有研究来解决此类问题,文献[7]使用人工势能场虚拟化环境,并通过势能值引入先验知识初始化Q值,进而提高Q-learning算法的收敛速度;文献[8]结合人工势场法,通过重新定义机器人的动作及步长来改进Q-learning算法,提高了算法收敛速度;文献[9]提出部分的Q学习概念,使用花授粉算法改善Q-learning算法的初始化,加快Q-learning算法的学习;文献[10]在传统的Q-learning算法基础上增加一层学习,使得机器人能够提前了解环境,进而加快路径规划效率;文献[11]为了加快Q-learning的学习速度,提出了一种集成学习策略;文献[12]限制了状态数,进而通过减小Q值表的大小提高了算法寻优速度;文献[13]研究了连续的报酬函数,使得机器人采取的每个动作都能获得相应的报酬,提高算法的学习效率。
虽然目前已有许多方法被提出来优化Qlearning算法,但是移动机器人寻找最佳路径依旧是一个值得研究的问题。本文主要针对Qlearning算法进行路径规划时所面临的学习效率低、收敛慢的问题,提出一种基于Q-learning算法的启发式算法(HQL)。首先根据移动机器人在工作环境中当前点和终点的相对位置来选择当前状态下的动作集,使机器人始终朝目标点前进,来提高学习速度;然后,在算法中引入启发式奖励机制,使得机器人在选择靠近终点的动作时收获更多的奖励,进而减少机器人盲目学习。最后在栅格环境中进行仿真实验,验证该算法的性能。
1 Q-learning算法
Q-learning算法是Watkins等提出的一种强化学习算法,也是时序差分算法中最常用的算法之一。其主要采用异策略评价估值的方法,这种方式也在很大程度上促进了Q值的迭代更新。Q-learning算法会根据机器人上一次所处的状态信息和当前学习所获得的奖励,通过式(1)来不断地更新自身维护的Q值表,进而当Q值表收敛时,机器人能从中选出最佳的状态-动作对,得到最优策略。
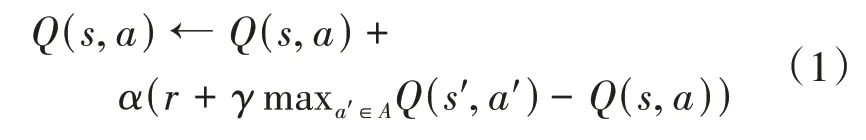
式(1)中,为学习率,表示学习新知识的程度,取值在0到1之间;是状态下采取行动时的奖励;为折扣率,表示考虑未来奖励的程度,取值在0到1之间;为下一个状态,为下一个动作。
2 HQL算法
传统的Q-learning算法在初始化过程中会将值设为均等值或随机值,也就是说,算法在初始阶段属于盲目学习,这在一定程度上降低了算法的学习效率。同样地,传统算法会在固定的动作集中选择动作,由于算法的动作选择策略存在一定的随机性,因此机器人会存在冗余学习,进而出现规划路径不佳的情况。针对这些问题,本文在传统的Q-learning算法的基础上做出如下两种改进,提出了改进的Q-learning算法。
2.1 动态动作集策略
传统的Q-learning算法的动作集是固定的,一般是上、下、左、右四个动作或是增加四个斜向动作的八个动作。根据算法的动作选择策略,机器人在选择动作时,存在一定的概率会随机选择动作集中的动作,故机器人所选的动作可能会使其远离终点,进而影响机器人的学习效率。鉴于常识,当我们出发去目的地时,一般会有意识地朝着目的地前进,这样才会使我们尽快到达。由此,提出动态动作集策略,使得机器人的每一步都能朝着终点前进。
动作集选择策略的主要思想是根据机器人当前所处的位置与终点的相对位置来给机器人分配动作集。本文以移动机器人的终点为参照,将算法的动作集分为如图1所示的八种情况,然后根据式(2)判断,此时机器人应该选择哪一个动作集。

图1 八种动作集

式(2)中,,分别为移动机器人当前位置的横、纵坐标,x,y分别为终点的横、纵坐标。机器人在某一状态进行学习之前,会先将机器人当前坐标与终点坐标进行运算,当(xx )*(-y )>0且-x <0时,即d *d >0,d <0,机器人选择第一种动作集,即图1(a)所示动作集进行学习;当(-x )*(-y )=0且-x <0时,即d *d =0,d <0,机器人选择第二种动作集,即图1(b)所示动作集;以此类推,式(2)中第3至第8条距离条件依次对应图1(c)至图1(h)所示的动作集。
2.2 启发式奖惩函数
Q-learning算法是无模型的学习算法,存在盲目学习的问题。为使机器人刚开始学习的时候就有意识地朝着终点的方向学习,在一定程度上减少盲目学习,进一步加快算法的学习速度,本文从算法的奖惩函数出发,通过使机器人采取不同的动作获得不同的奖励来指导机器人学习环境。若机器人采取的动作使其更接近终点,则获得更多的奖励;反之,则获得的奖励会减少。
本文中传统的Q-learning算法奖惩函数设置如式(3)所示。

引入启发式奖励后的奖惩函数设置如式(4)所示。

其中,r 为Q-learning算法设置的奖惩函数,,分别为移动机器人当前位置的横、纵坐标,x,y分别为终点的横、纵坐标。
2.3 流程设计
运用HQL算法进行路径规划步骤如下:
(1)初始化算法的值表;
(2)判断机器人总的学习次数是否小于5000,若是,进入(3),若否,则结束学习;
(3)初始化状态;
(4)根据策略选择动作集;
(5)从动作集中选出下一步动作并执行;
(6)根据执行动作后的状态得到相应的奖励r;
(7)根据式(1)计算并更新值表;
(8)进入下一个状态;
(9)判断此时机器人所处的状态是否为终点,若是,则返回(2)进入下一次学习,若否,则返回(4)。
3 实验及结果分析
本文实验使用Python进行编译,实验采用30×30的二维栅格地图来表示整个环境信息。其中,左下圆点代表机器人的起点,右上圆点代表终点,实心方格表示障碍物,白色区域表示可移动区域。在仿真实验中,传统Q学习算法和本文算法学习过程中的实验参数值设置如下。折扣因子表示考虑未来奖励的程度,本文采取一个折中的方式,设为0.5。同时经过多次尝试与试验,将尝试次数即机器人总的学习次数设为5000,学习率和探索因子的初始值分别设为0.8和0.3,使机器人能够得到更加充分的学习且算法性能更加稳定。
在栅格地图中对本文所提的改进算法与两种传统Q-learning算法进行验证,证明本文的改进算法在规划路径的长度和学习效率方面的优势。图2(a)、(b)分别为表1中传统Q-learning算法(QL_0)和本文算法(QL_2)在栅格地图中生成的最优路径。
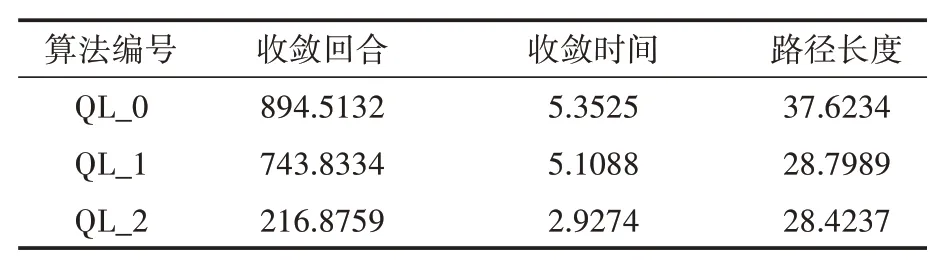
表1 学习算法在路径规划中的性能比较
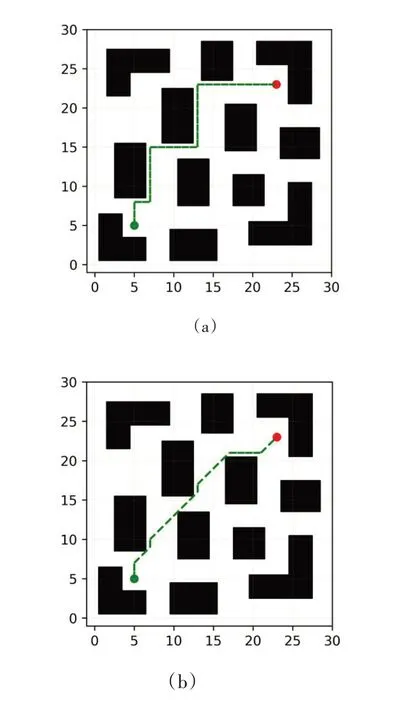
图2 算法规划的路径图
表1中算法的收敛回合、收敛时间和路径长度均为30次实验数据的平均值,QL_0算法表示动作集为上、下、左、右的传统Q-learning算法;QL_1算法表示动作集为上、下、左、右、右上、右下、左上、左下的传统Q-learning算法;QL_2为本文所提算法。在算法收敛的判断中,本文主要根据连续10次尝试回合路径长度标准差小于0.25即视为算法收敛。
从表1可知,将本文所提算法即QL_2与传统的四个动作的Q-learning算法即QL_0进行对比,算法的收敛回合提前了75.8%,收敛时间减少了45.3%,规划的最终路径长度缩短了24.5%。对比QL_1和QL_0可知,仅仅增加算法的动作数,虽然很大程度上缩短规划路径的长度,但是并没有明显加快算法的收敛速度。根据表1的数据,相较于QL_0和QL_1这两种传统学习算法,本文所提算法在不增加动作数的情况下不仅能够缩短规划的路径长度,同时也能达到使算法更快收敛的目的。
4 结语
基于马尔可夫决策过程的Q-learning算法在路径规划应用中一般可以找到到达终点的路径,但是其在复杂环境下进行路径规划时学习效率低、收敛速度慢,由此提出了基于Q_learning算法的启发式算法(HQL)。首先,学习算法是通过选择每个状态下最优动作的方式来完成路径规划,每一次的动作选择都在一定程度上影响机器人的学习效果,故本文从源头出发,通过控制动作集来使机器人进行更有效的学习,提高学习效率;其次,通过在算法中加入启发式奖励,机器人的每一个动作都能得到不同的奖励,使得机器人能够朝着终点运动,进一步加快其学习。最后从仿真实验结果可以看出,相较于传统的学习算法,本文所提算法性能更优。

