电梯价格预测中的数据预处理方法研究
胡 昱,胡兆勇,何汉武,张 研,林穗贤
(1.广东工业大学机电工程学院,广州 510006;2.广州广日电梯有限公司,广州 511441)
0 引言
价格预测是一种为了做出更好价格决策的辅助方案,企业通过研究历史交易数据得出价格的变化规律和影响因素,从而实现价格的预测。在电梯行业,定制电梯的价格预测主要是通过分析用户在驱动系统、材质、工艺、性能、部件质量、品质感等方面的需求,再结合电梯设计、制造以及安装的成本与历史数据进行对比和评估,进行一个粗略的价格预测;而在其他行业,传统的价格预测也是通过市场调研、人工统计的方法实现,这种方式不仅费时费力,还可能出现人为误差甚至错误。随着数据挖掘和人工智能技术的发展,价格的预测打破了传统预测方法的局限性,通过神经网络学习数据中的规律完成预测,这种方法不仅能够提高价格预测的效率,还能够提高预测的准确性。
1 数据预处理技术
在基于机器学习的价格预测中,数据的预处理是最重要的一步,其中特征表示能够决定预测结果的好与不好。数据预处理通常分为数据清洗、数据集成、特征表示和特征选择。数据清洗就是通过一定规则与标准将原始数据中的脏数据删除或转化为干净数据;数据集成将多源复杂数据按照一定的属性规律集中起来,便于处理;特征表示就是找到特征最合适的表示方式提取数据中的特征信息;特征选择是提取与结果具有高度相关性的特征,去除冗余无关特征,提高机器学习的效率。不少学者对预测中的数据预处理方法开展了研究,文献[7]在数据预处理中通过特征历史趋势的空间变换表示特征,通过卡方分析和相关系数选择影响价格的主要特征,通过主成分分析法去除冗余特征,通过LSTM模型实现中短期电煤的价格预测。文献[8]在数据预处理中通过Pearson相关系数去除特征之间具有强相关性的冗余特征,通过主成分分析法对特征降维,通过基于粒子群的SVM实现电动车价格预测。文献[9]在数据预处理中通过相关系数去除冗余特征,通过基于密度最大值聚类算法处理特征的离群值,通过最小基尼指数提取特征,通过HMM模型实现股票价格行为预测。文献[10]介绍数据预处理的常用方法,可以通过函数变换、函数映射和归一化实现特征变换,通过LVF、MIFS、mRMR、Relief和PCA算法实现特征降维,通过MDLP、ChiMerge、CAIM实现连续数据的离散化。
当前在数据预处理方法的研究中,数据主要聚焦在数值型、类别型和时间型数据,往往不涉及对空间型和矩阵型数据的处理,同时对于参数繁多且特征复杂的电梯设备价格预测的数据预处理方法研究甚少。所以以电梯设备作为研究对象,电梯交易数据作为数据源,对电梯价格预测的数据预处理方法进行研究。主要研究内容包括:①基于类型聚类的特征标准化表示,根据不同类型特征的特点对数据进行聚类,并根据这些特征特点采取不同的方法对特征进行有效的表示,最大程度提取数据中的信息;②基于信息增益的特征选择,从大量特征中精确提取出关键特征,去除相关度较低或者无关的冗余特征,从而提高神经网络的训练速度和预测的准确性。
2 电梯价格预测的特征表示和选择
2.1 基于类型聚类的特征标准化表示
电梯合同中的参数包含地区、控制系统、梯种、额定速度、轿厢净高、层门板厚等共515个参数,其中包含必选参数(梯种、额定速度等)和可选参数(数字视频监控功能等),电梯参数数据表如表1所示。

表1 电梯参数数据表
由表1可知,电梯价格预测的影响因素复杂,尽管这些特征能够为机器学习模型提供有效的信息,但对特征不合理的表示会适得其反,降低预测准确率,所以需要实现更合理的特征表示,从而使价格的预测更加准确可靠。通常在数据预处理中会采用数据轮询的方式对特征进行表示,这样处理的效率较低,所以可以通过聚类的方法来加速处理过程。依据不同的特征特点,采取与之相对应的表示方法。首先通过聚类的方法将特征分成五类,即数值型特征、类别型特征、时间型特征、空间型特征和矩阵型特征,再对每一种特征进行标准化表示。
数值型特征是只包含数值的特征类型,例如额定速度、梯种台数、安全门数量等。在基于机器学习的价格预测中,数值型数据是可以被机器学习模型接受和理解的数据,所以对于数值型数据的表示,可以通过数据变换的方法,将所有数值映射在一个区间内,小数值被相对扩大,大数值被相对压缩,使所有数值分布更加均匀,避免取值范围过大的特征影响训练速度和精度。
类别型特征指的是具有不同性质和特点能够代表不同类别的特征,由字符组成,如层门材料、吊顶型号等。对于字符格式的特征,需要通过编码的方式将字符转化为数值。对于无序的类别型特征,采用的是独热编码。通过N位状态寄存器来对个状态进行编码,每个状态都有独立的寄存器位,在任意时候只有一位状态寄存器有效,从而使机器学习模型在计算具体特征间的欧氏距离更加合理,独热编码如表2所示。

表2 独热编码
对于有序的类别数量较大的特征列使用独热编码会增加特征的总维度,并使特征变得稀疏,从而降低机器学习训练的效率和预测准确度,所以需要引入不同的编码方法-标签编码,即通过将不同类别映射为不同的自然数,以停站层数为例,其标签编码如表3所示。

表3 标签编码
时间型特征指的是按其发生的时间先后顺序排列而成的具有时间序列特点的特征,由字符组成,可以是年份、季度、月份或者其他任何时间形式,例如签订日期。对于该类特征,采用切分提取时间的方法对时间进行切分,转化为年、月和日,从而将字符转化为数值类型,时间型特征的表示如表4所示。

表4 时间序列特征表示
空间型特征指的是对具有定位意义的事物的定量描述,由字符组成,例如地区。空间型特征不能直接通过独热编码和标签编码处理,因为这不仅会极大地增加特征维度,还会出现表示不准确的问题,所以对于该类特征,采用映射再编码的方式。对于广东省内的地区,映射为类“省内”;对于广东省外以及中国内的地区,映射为类“省外”;对于国外的地区,映射为类“国外”,然后再通过独热编码进行表示,空间型特征表示如表5所示。

表5 空间特征表示
矩阵型特征指的是按照矩阵形式存储的特征,由字符组成,矩阵内的元素是数值型特征或类别型特征,例如“int,int...”或“category,category...”。对于矩阵型特征,假设每一个单元格内的一维矩阵中有个元素,可以将一维矩阵特征按行合并为多维矩阵,同一索引位置的元素属于同一个子特征列,采用降维的方法将个子特征列变为(<)个子特征列表示原特征。矩阵型特征表示的步骤如下:
(1)若矩阵特征共有行,沿行方向合并矩阵特征中的所有数据,若矩阵内的元素为字符,将字符映射为数值,合并后得到一个N×M的矩阵;
(2)对矩阵的列向量去中心化;
(3)对矩阵进行转置,得到矩阵;
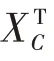


(7)对特征值按从大到小的顺序排序,并设定方差贡献率,通过方差贡献率筛选排在前的个特征向量作为线性变换矩阵;
(8)由=,线性变换矩阵右乘以矩阵,得到变换后的新矩阵,使用新矩阵替换原矩阵。矩阵型特征表示如表6所示。

表6 矩阵特征表示
2.2 基于信息增益的特征选择
特征标准化表示后,特征中仍然包含冗余非关键特征,为了进一步提高神经网络训练的速度和价格预测的准确性,需要使用特征选择方法。特征选择从已有的W个特征中选取S个特征,去除冗余非关键特征,减小特征总维度,避免相关性小和无关特征影响机器学习训练过程,从而提高算法性能。
提出一种基于信息增益的特征选择方法进行特征选择,步骤如下:
(1)特征子集构建。利用Xgboost算法计算每个特征的重要程度,即每个特征的信息增益。该算法在构建树的过程中,通过对参与构建的特征的平均信息增益值(AverageGain,AG)进行统计,得到不同特征的平均信息增益值,如式(1)所示。
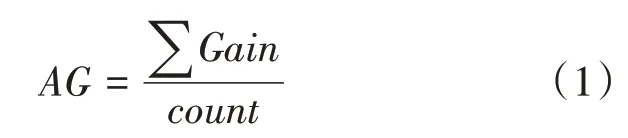

将增益值从大到小进行排序,设定一个特征重要度阈值,通过该阈值划分为高重要度和低重要度的特征子集;若在低重要度的特征子集中存在与高重要度子集中的特征互为系列的特征(独热算法得到的系列特征),则加入到高重要度特征子集中去,构成局部最优的特征子集。
(2)最优子集选择。通过更新重要度阈值,可以得到不同的特征子集,再根据不同特征子集得到不同的预测结果,比较和选取最优的特征子集。
基于信息增益的特征选择流程图如图1所示。

图1 基于信息增益的特征选择流程图
3 实验验证
3.1 实验设计
3.1.1 数据集选用
数据集采用企业的电梯交易数据,为客观验证算法的整体性能,选取两份较完整的数据集进行实验。数据集的描述如表7所示。

表7 矩阵特征表示
3.1.2 预测模型
在价格预测中常用的算法有:LSTM、Ada⁃boost、DNN、KNN等。通过大量实验发现深度神经网络在上述数据集上有较好的表现,所以选用深度神经网络作为实验的机器学习模型。对上述数据集进行预处理后再训练深度神经网络,进而完成价格的预测。
3.1.3 评价指标
数据质量的高低直接影响预测结果的准确性。对于数据预处理方法有效性的判断,可以转化为对模型性能的评价。通常模型表现较好,即预测结果较准确,可以反映出输入的数据质量较好。对于回归预测模型,使用决定系数(Rsquare)、解释方差分数(Explained Variance Score)、平均绝对误差(Mean Absolute Error)、均方根误差(Root Mean Square Error)等指标对模型性能进行评价。
(1)决定系数(R-square,)表示在回归关系中,因变量的变异中可由自变量解释部分所占的比例。从机器学习的角度来说,就是因变量与自变量间的线性相关程度,即模型对预测值的拟合程度,定义为:


(2)解释方差分数(Explained Variance Score,EVS)表示在给定数据中的变异能被模型解释的部分,与决定系数相似,定义为:


(3)平均绝对误差(Mean Absolute Error,MAE)表示观测值与真实值的偏差与观测次数的比值,描述预测值和真实值的差值,定义为:


(4)均方根误差(Root Mean Square Error,RMSE)表示预测值与真实值偏差的平方与预测次数比值的平方根,用于衡量真实值与预测值的偏差,定义为:


上述评价指标中决定系数与解释方差分数的取值范围通常为[0,1],越接近1说明模型拟合效果越好;平均绝对误差、均方根误差的取值随y值大小变化,无固定取值范围,但是其值越小,拟合效果越好。
3.1.4 实验内容
为了验证特征表示和特征选择方法的有效性,设计了如下实验:①基于类型聚类的特征标准化表示;②基于信息增益的特征选择的验证。
3.2 实验结果与分析
3.2.1 基于类型聚类的特征标准化表示的验证
通过采用类型聚类特征表示方法和文献[15]特征表示方法分别处理数据后建立预测模型进行对比实验,使用的数据集为“整梯1”和“整梯2”。为了避免结果的偶然性,对数据集按不同比例进行划分后实验,实验结果如表8和表9所示。

表8 不同特征表示方法在整梯1上的评价指标对比
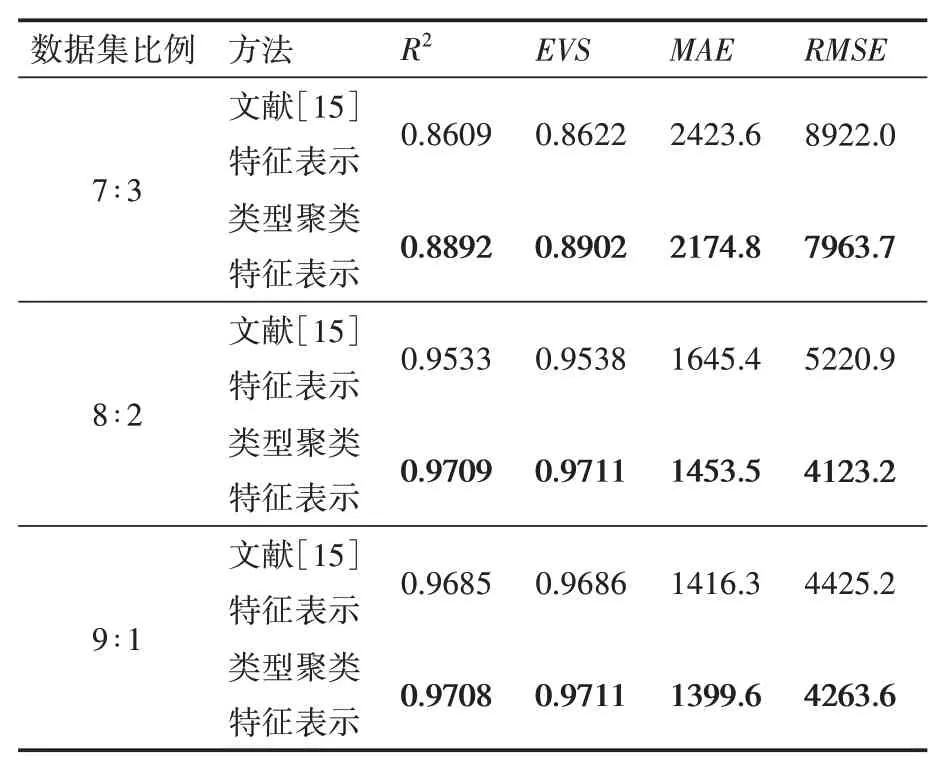
表9 不同特征表示方法在整梯2上的评价指标对比
由表8和表9可知,对于数据集整梯1和整梯2,在按不同比例划分数据集的实验中,类型聚类特征表示方法相较于文献[15]特征表示方法,、、、都有不同程度的改善。经计算,对于数据集整梯1,和平均都提高了1.4%,、RMSE分别平均下降了2.3%和7.2%。对于数据集整梯2,、平均都提高了1.8%,、分别平均下降了7.7%和11.8%。
为了进行更直观的对比,将上述实验中得到的评价指标平均化,分别计算整梯1、整梯2中、、、的平均值,并使用柱状图展示对比,如图2和图3所示。

图2 不同特征表示方法R 2与EVS对比

图3 不同特征表示方法M AE与RMSE对比
由上述结果可知,类型聚类特征表示方法优于文献[15]中通用的特征表示方法,在按不同划分比例的不同数据集上的评价指标均有所提升,所以该实验证明了基于类型聚类的特征标准化表示方法的有效性。
3.2.2 基于信息增益的特征选择的验证
分别对是否通过特征选择处理特征表示后的数据建立模型,并进行对比实验,使用的数据集为“整梯1”和“整梯2”。对数据集按不同比例进行划分后实验,实验结果如表10~表13所示。
由表10~表13可知,对于数据集整梯1和整梯2,在按不同比例划分数据集进行特征选择的实验中,不论是决定系数、解释方差分数等评价指标,还是维度缩减和训练时间等其他指标,都有不同程度的改善。对于数据集整梯1,、平均都提高了4.8%,、分别平均下降了6.8%和53.6%,训练时间平均下降了47.3%,特征数也由599个缩减到129个。对于数据集整梯2,、平均都提高了3.5%,、分别平均下降了1%和45%,训练时间平均下降了61.2%,特征数也由732个缩减到92个。

表10 整梯1特征选择前后的评价指标对比

表11 整梯1特征选择前后的其他指标对比

表12 整梯2特征选择前后的评价指标对比

表13 整梯2特征选择前后的其他指标对比
为了进行更直观的对比,将上述实验中得到的评价指标平均化,分别计算整梯1、整梯2中、、、的平均值,并使用柱状图展示对比,如图4和图5所示。

图4 特征选择前后R 2与E V S对比

图5 特征选择前后M A E与RM S E对比
由上述结果可知,当数据量较大时,该特征选择方法不仅可以去除冗余和无关特征,降低了模型的计算复杂度,减少了训练耗时,还提高了模型预测的准确率,所以该实验证明了基于信息增益的特征选择方法的有效性。
4 结语
通过改善数据预处理中的特征表示和特征选择方法提高价格预测的准确率,提出了一种基于类型聚类的特征标准化表示和基于信息增益的特征选择的数据预处理方法。该方法通过对不同类型的特征进行聚类,根据不同特征的特点采用不同且合适的方法进行特征表示,其中利用方差贡献度和降维的思想提取矩阵特征的信息;之后通过特征的信息增益选择关键非冗余特征,最后在两份数据集中进行对比实验。实验结果表明,提出的基于类型聚类的特征标准化表示方法和基于信息增益的特征选择方法能够使价格预测准备率提升。由于文中涉及的数据集不包括信号波形与图像等非结构化数据,所以提出的数据预处理方法不适用于非结构化数据的预处理,这是该数据预处理方法的不足之处,今后还需要针对非结构化数据的预处理问题进行研究。

