基于银行动态多层网络的系统性风险防控政策效果研究

李守伟 王 虎 刘晓星

(东南大学 经济管理学院,江苏 南京 211189)

0 引言

2007-2009 年的全球性金融危机直接催生了巴塞尔协议III。巴塞尔协议III 在原有标准基础上对流动性监管提出了更高的要求,第一次将监管约束和市场约束机制纳入到资本框架中,对金融系统的监管逐渐从关注单一金融机构的微观审慎理念向整个金融系统的宏观审慎理念转变,防范系统性风险的发生成为监管的重点[1]。基于此,中国银监会依据巴塞尔协议III,针对我国商业银行监管发布了《商业银行资本管理办法》。党的十九大报告和中央经济工作会议提出了“守住不发生系统性金融风险的底线,将防范化解金融风险和服务实体经济更好结合起来”的要求,并提出了“货币政策+宏观审慎政策”的双支柱政策框架。通过稳健的货币政策和宏观审慎政策相结合,这能够在保持经济平稳运行的同时,有效地防范和化解系统性风险。

历次金融危机表明,银行间市场在风险传染中扮演了重要角色[2]。在我国金融体系中,由于银行部门在间接融资方面的主导作用,我国金融系统中大部分风险都集中在银行系统中[3]。近年来,我国逐渐放开衍生品市场,但我国的金融衍生品交易主要集中在银行间。根据《银行间市场运行报告》,利率衍生品和外汇衍生品市场交易规模分别从2010 年的1.5 万亿元和1.3 万亿美元增加到2018 年的21.6 万亿元和17.3 万亿美元。2007-2009 年金融危机的直接原因就是信用违约互换(CDS),衍生品市场的高风险性使得其在防范银行系统性风险发生的过程中具有重要作用,忽视衍生品市场会严重低估银行系统性风险[4]。时间维度上,银行系统和实体经济部门之间的加速器机制形成了风险反馈效应;空间维度上,不同银行间通过不同金融市场形成复杂金融关联放大了系统性风险[5]。由于银行系统在时间维度和空间维度与实体经济和金融市场的关联性,在宏观审慎监管约束下,货币政策工具对金融系统调节会产生溢出效应[6]。虽然宏观审慎政策和货币政策分别在稳定经济系统和降低系统性风险中具有重要作用,但两者结合并不一定能够起到一加一大于二的政策效果,宏观审慎监管政策可能会改变货币政策的传导机制,造成“政策冲突”和“政策叠加”,降低政策效果和增加政策实施成本[7-9]。基于此,本文有必要从银行系统多层金融关联的角度分析宏观审慎政策和货币政策相结合对银行系统的影响。

本文在Wolski 和van de Leur 同业拆借关联模型的基础上[10],引入衍生品交易关联和持有共同资产关联,构建了银行动态多层网络模型。文献[10]中的银行间市场模型仅考虑银行间的同业拆借交易关联以及同业拆借交易的直接风险传染渠道。而本文构建的银行动态多层网络模型,包括同业拆借交易形成的同业拆借关联、衍生品交易形成的衍生品关联以及持有相同资产形成的持有共同资产关联,并且同时考虑同业拆借和衍生品交易两种关联的直接风险传染渠道以及持有共同资产关联的间接风险传染渠道。实际中,银行风险往往产生于少数金融机构或者单一金融市场,风险通过不同传染渠道在不同金融市场间传染,而不同传染渠道和金融市场间的相互作用会放大最初风险对整个金融系统的影响[11]。本文的研究可以较为全面准确地分析风险在不同传染渠道和金融市场间的传染机制以及不同监管政策和货币政策工具对银行系统的影响。本文的主要贡献为:(1)现有对银行系统性风险监管的研究主要集中于单层网络,并忽视了衍生品市场对风险在银行系统中传染的影响,本文构建的银行动态多层网络模型将衍生品交易网络纳入到整个银行系统中,从多层网络的角度对银行系统性风险防控进行研究。(2)考虑了银行的流动性囤积行为以及证券抛售导致资产价格下跌过程,包括了直接和间接两种风险传染渠道。(3)分析了宏观审慎政策和货币政策工具以及两种相结合通过不同金融市场作用于整个银行系统的传染机制,以及如何综合利用宏观审慎政策和货币政策工具保证整个银行系统的平稳运行。

1 文献综述

金融危机后,从宏观审慎角度对银行系统性风险监管进行研究成为关注的热点。如Gai 等建立了一个以无担保债权、回购活动和抵押物折价冲击为中心的银行同业拆借网络模型。模型结果表明,银行网络的复杂性和集中度可能会放大银行系统的脆弱性,而更严格的流动性监管、宏观审慎政策,以及对具有系统重要性的银行收取附加费,能够增加银行系统的稳定性[12]。Kiema 和Jokivuolle 研究了非风险加权杠杆率要求(LRR)对贷款策略和银行稳定性的影响,认为如果非风险加权杠杆率要求低于银行平均的内部评级的资本金要求,可能会降低银行系统的稳定性[13]。Hałaj 和Kok 通过构建内生银行网络系统,分析了信用风险评估调整(CVA)和大额风险敞口对银行间网络结构以及风险传染机制的影响[14]。Hugonnier 和Morellec 基于构建的动态银行模型,指出强制实施流动性监管要求会降低银行的违约损失,但是会增加违约概率,而同时实施流动性和杠杆监管,既降低了违约概率,也降低了银行违约损失[15]。除了通过构建银行网络模型分析银行系统性风险外,也有一些学者从实证的角度进行了研究。如黄敏等基于2002-2014 年中国127 家商业银行数据,分析了资本监管、信息披露质量对银行风险承担影响,认为严格的资本监管和高质量的信息披露可以抑制银行风险承担行为,并且信息披露质量对资本充足性较低的银行影响更加显著[16]。王连军利用我国120 家银行的面板数据分析了去杠杆化对银行稳定性的影响。结果表明,虽然去杠杆化在短期内会对银行经营稳健性产生影响,但长期来说,去杠杆化降低了银行破产率和提高了经营稳健性[17]。杨子晖和李东承通过对中国177 家银行的系统性风险的研究,发现股份制商业银行是银行业系统性风险的主要诱发者,并提出建立以资本充足率为核心,以杠杆率、风险暴露和银行间负债为重点的银行业风险监管方法[3]。

上述研究从风险资本监管、杠杆水平、流动性、大额风险暴露和市场约束等宏观审慎监管角度进行了分析。此外,巴塞尔协议III 增加了对衍生品资产信用估值调整,提出应通过中央对手方进行衍生品交易。国内针对衍生品市场的研究较少,国外对衍生品市场风险监管的研究主要集中在中央对手方的中央清算和保证金制度两个方面。如Duffie 和Zhu 构建了包含中央对手方(CCP)的场外衍生品交易模型,认为对某一类衍生品进行集中清算可能会降低净效率,通过单一中央对手方清算组合衍生品会比在多个中央对手方中清算组合衍生品更加有效[18]。Cont 和Kokholm 基于Duffie 和Zhu 的思路研究了集中清算对交易对手风险敞口的影响,认为中央对手方对预期交易对手风险敞口的影响由交易商之间的多边净收益与资产类别之间的双边净收益共同决定,并且当存在利率衍生品时,增加中央对手方会降低风险敞口[19]。也有研究认为,极端情况下,中央对手方可能会增加银行系统流动性风险[20-21]。在保证金制度对银行系统的影响方面,Gibson 和Murawski 通过构建动态银行均衡模型,认为保证金增加了违约风险,减少了衍生品的总交易量[22]。Glasserman 和Wu 基于GARCH 波动率模型,指出波动性的持续性和突发性越强,避免顺周期性所需的保证金水平越高[23]。Bakoush 和Gerding认为保证金顺周期性所造成的困境会蔓延到银行间市场,会导致系统性的流动性风险,并且银行间的相互联系进一步放大了银行间市场内系统性风险的影响[24]。

货币政策不仅能决定宏观经济稳定,而且会对银行系统性风险产生影响。很多实证研究表明,货币政策会通过风险承担渠道对银行系统稳定产生影响。如张强等和金鹏辉等从银行信贷行为的角度证实了货币承担渠道的存在,并且货币政策会对银行风险承担产生显著影响[25-26]。Dell′Aricci 等基于美国商业银行数据,证实了短期利率下降会增加银行的风险承担,进而对银行系统稳定产生影响[27]。项后军等通过渠道识别分析了利率追逐机制对银行风险承担的影响,认为实际利率越低于政策利率,银行利率追逐的激励就越大,银行风险承担越高[28]。邓向荣和张嘉明从流动性创造的角度分析货币政策通过银行风险承担对银行系统的影响,认为不同类型的货币政策工具对银行风险承担都具有显著影响,而且通过银行风险承担的中介作用,对银行流动性创造产生显著影响[29]。此外,也有很多基于DSGE 模型和复杂网络理论,从网络结构、担保机制、互联网金融和货币政策传导机制等角度对货币政策对银行系统稳定的影响进行了研究[10,30-33]。

巴塞尔协议宏观审慎的监管理念提出后,学者从宏观审慎政策和货币政策相结合的视角对银行系统稳定性的影响进行了大量的研究。很多研究证实了两种政策结合能形成互补,有利于金融系统的稳定。如Rubio 和Carrasco-Gallegob研究巴塞尔I、II 和III 规则与货币政策之间的相互作用,认为与巴塞尔I、II 相比,宏观审慎的监管政策和货币政策相结合更有利于金融稳定[34]。Malovana 和Frait 通过对5 个欧元区国家的数据分析,发现宽松货币政策加剧了金融系统脆弱性的累积,推高了信贷周期,而宏观审慎的资本监管有助于缓解货币政策对金融系统的风险累积[35]。Popoyan 等基于主体的模型分析,认为货币政策和宏观审慎监管在增强银行系统稳定和改善经济表现是相辅相成的,并且资本充足率和反周期资本缓冲的监管框架效果最好[36]。Garcia Revelo 等指出限制性货币政策增强了宏观审慎紧缩对信贷增长的影响,并且有助于减少宏观审慎政策行动的传导延迟[37]。在国内的研究中,文献[9,38-40]均发现两种政策结合更有利于维持金融系统和宏观经济稳定。也有研究指出两种政策结合可能会造成政策重叠,并且政策效果取决于两者的协调。如马勇和陈雨露基于内生性金融体系的DSGE 模型框架分析了货币政策和宏观监管政策的协调搭配问题,分析认为需要避免“政策冲突”和“政策叠加”问题,前者会削弱政策效果并增加政策实施的成本,而后者则可能导致经济系统以一种非预期的方式进行调整[7]。Borio 和White 指出货币政策和宏观审慎监管会导致目标冲突,造成经济波动,并且货币政策工具在防范化解金融风险上的效果有限[8]。Angelini 等认为宏观审慎政策和货币政策由于作用目标的不同,如果不能很好地协调,宏观审慎政策可能会降低金融系统稳定[41]。李建强等认为经济周期与金融周期不同步时,宏观政策调控存在政策工具冲突和叠加隐患,当财政部门与中央银行缺乏协调合作时,“非预期效果”会降低社会福利水平[42]。

纵观上述研究发现,针对银行系统性风险监管的研究主要通过实际数据进行实证分析和构建银行系统模型。但现有银行系统模型主要集中在单一金融市场,并且多为单层银行网络,而现实中银行主体通过不同金融市场形成复杂的金融关联,风险通过不同金融关联在银行系统中传染。基于多主体的银行系统模型可以通过模拟微观主体行为之间的相互作用而反映出系统整体的宏观特征,并且能有效地评估政策工具对银行系统的影响和提高决策者对政策工具的理解[14]。因此,本文通过构建银行动态多层网络模型分析银行系统性风险多渠道传染机制,有效地弥补了单层银行网络模型的缺陷。

2 模型

本文基于资产负债表刻画银行行为,假设银行资产负债表组成如表1 所示。其中,资产部分包括债券资产①债券是指政府发行的国债,用以表示基准利率。假设在债券市场中,债券供应量为无限,与其他投资相比,债券投资风险最低。设定初始债券利率为,利率波动范围服从均值为零标准差为γB 的正态分布。、同业资产、衍生品资产、证券资产②证券资产表示除债券之外的股票、基金等较高风险证券资产。假设证券市场中所有证券均为同质的,证券收益遵循几何布朗运动:,其中预期收益πt=-1 和波动σt=σmin·分别由抛售证券比例和违约银行比例dt 决定[45],α 表示市场流动性水平,∂t 服从标准正态分布,σmin 和σmax 分别表示证券收益波动的最小值和最大值。、其他投资资产③其他投资市场可以看作是对实体经济投资,是由大量投资项目组成。投资项目的平均收益和风险水平分别为在区间(0,ψ) 和区间(0,γS) 内均匀分布,并假设收益和风险成正比关系。在进行资产分配之前,每家银行会随机选择投资项目,并且知道投资项目的平均收益和风险的具体分布。和现金,负债部分包括储蓄、同业负债、衍生品负债、其他负债和净资产。银行主体行为涉及债券、证券、同业拆借、衍生品和其他投资五个金融市场。通过同业拆借、衍生品交易和持有共同资产,银行间形成了同业拆借交易关联、衍生品交易关联和持有共同资产关联。将银行作为节点,银行间关联作为边,则形成了银行多层网络结构,具体为同业拆借网络、衍生品网络和持有共同资产网络三层。而银行主体行为在不同时刻是变化的,进而导致银行间关联是在变化的,而此形成了银行动态多层网络,如图1 所示。下面从同业拆借交易机制和衍生品交易机制刻画银行动态同业拆借和衍生品交易行为以及基于同业拆借和衍生品交易的直接风险传染渠道,证券市场投资刻画了持有共同资产的间接风险传染渠道,中央对手方为衍生品交易提供中央清算,投资决策机制刻画了银行动态预测策略和资产分配行为,进而形成了银行动态多层网络模型。

表1 银行资产负债表Table 1 Banks′ balance sheets

图1 银行动态多层网络Figure 1 Dynamic multilayer network of banks

2.1 同业拆借交易机制

在同业拆借市场中,本文借鉴Delli Gatti 等提出的优先交易匹配机制来刻画银行间同业拆借交易行为[43]。在Delli Gatti 等的研究中,银行更换交易对手的概率取决于交易利率,而本文与此不同,本文假设银行更换交易对手的概率同时受到之前交易次数和交易利率的影响。并假设银行进行借款和贷款所提供的利率与其预期一致[10]。首先,借款银行会随机选择一定数量潜在的贷款银行,并观察这些随机选择的贷款银行提供的利率。一般情况下,银行会倾向于与旧的交易对手进行交易,但由于银行的趋利性,如果有的新的潜在交易对手提供了更低的贷款利率时,则有一定的概率与新的银行进行交易。这个概率proI为:

其中B(i,j)表示银行i和银行j在同业市场的交易次数,更换交易对手的概率取决于两者之前交易次数和新的交易利率,并且满足υ1+υ2=1。如果观察到的潜在新交易对手设定的最低利率rnew大于或等于前交易对手的利率rold,则借款银行将继续与当前贷款银行进行交易。如果不是这种情况,则新银行以proI的概率替换之前的交易银行。

借款银行根据优先交易对手匹配机制向贷款银行申请贷款,如果其借款需求不能得到满足,则借款银行继续向其他贷款银行申请贷款,直至其对借款需求完全得到满足或者银行市场无多余流动性可供分配。如果贷款银行的贷款金额能满足其所有的潜在的借款主体,潜在的借款主体成为其真实的借款主体。相反,如果贷款银行的贷款金额不能满足所有的借款主体的贷款申请。此种情况下,银行随机选择借款银行进行贷款需求分配。

银行提供或要求的每一时期利率等于债券利率加上给定市场预期风险溢价[10]。通过违约风险和市场流动性风险的折现数来调整对风险溢价的预测,风险溢价包括违约风险溢价和流动性风险溢价。则t时刻的折现数可以表示为qt=≥0,nb表示破产银行数目,α表示市场流动性水平。

2.2 衍生品交易机制

Vuillemey 和Breton 与Heath 等对银行间的一般性衍生品交易机制进行了刻画[20,44],本文借鉴他们的思想刻画银行间衍生品交易。但本文的研究与他们不同之处在于以下三个方面:(1)本文中银行间衍生品交易为以同业拆借利率为标的物的期权交易,银行的衍生品交易行为取决于同业拆借利率的实际变化和对同业拆借利率的预期,并随同业拆借利率的实际变化而动态变化的。(2)银行间的衍生品交易对手选择遵循优先交易匹配机制,并且更换交易对手的概率同时受到之前交易次数和交易收益的影响。(3)根据每个时期交易结束时银行衍生品双边总名义头寸矩阵,计算得到每个时期衍生品市场风险敞口。本文中,每家银行对衍生品交易的投资由之前时刻对同业拆借利率波动的预测决定,同业拆借利率波动越大,则银行越倾向于通过衍生品交易来对冲同业拆借利率波动带来的风险。同时,衍生品交易获利的概率越大。银行i和银行j之间的衍生品交易定义为{wij,pij},wij表示交易合同的名义价值,pij＞0 表示合同买方所需要支付的单位费用,wij＞0 表示银行i卖出合同,wij＜0 表示银行i买进合同,并且wij=-wji,pij=pji。因此,合同买方银行i需要支付给卖方银行j的费用为-wijpij。假设银行i违约概率为λi。则交易{wij,pij} 的效用为:

U 为常数相对风险厌恶(CRRA)函数,并且连续可微,U(0)表示银行i违约时获得效用收益为0。设定风险期为10天,初始保证金为覆盖99%置信度条件下的风险敞口[46]。Ei,tri,t+1表示银行i在t时刻预测t+1 时刻的同业拆借利率,初始保证金和追加保证金在wij＜0 时均为0,表示只有合同卖方才会提交初始保证金和追加保证金,β表示初始保证金缴纳比例,ζ表示99%置信度对应均值的标准差个数,表示之前同业拆借利率波动率的平均值。当预期同业拆借利率上涨时,合同卖方需要支付追加保证金给买方。

假设任何衍生品不能被无限制的买卖,银行i所能买卖的合同数量取决于银行j所能提供的数量和购买的数量。任何机构都可以根据所提供的价格作为买方或卖方。在任意交易{wij,pij} 中,目标函数是具有同等议价能力的双方效用收益的纳什乘积。此外,两家银行都受到预算和参与限制。

第一个约束是银行i作为合同买方的预算约束,表示银行i购买合同的费用小于等于其分配给衍生品市场的资产。第二个约束是银行j作为合同卖方的预算约束,表示银行j卖出合同需要支付的初始保证金小于等于分配给衍生品市场的资产。第三个约束是银行i的参与约束,第四个约束是银行j的参与约束。衍生品价格是由所有交易的加权平均得到。每个时期交易结束后,可以得到双边总名义头寸矩阵W,通过双边总名义头寸矩阵与其转置矩阵的差值得到双边净名义头寸矩阵N=W-W′[20],则衍生品市场的风场敞口为∑i∑j|Nij|。

银行间的衍生品交易规则与同业拆借交易类似,每家银行会选择一定数量的潜在交易对手,并随机选择一家潜在的交易对手进行交易。交易完成后,若分配给衍生品市场的资产仍有剩余,则继续与其他潜在交易对手进行交易,而没有剩余资产的则不再进行交易,直到没有银行可以进行交易为止。同时,衍生品交易的约束条件根据交易而改变。在下一个时刻,每家银行更换新交易对手的概率proD为:

其中,C(i,j)表示银行i和银行j在衍生品市场的交易次数,更换交易对手的概率取决于两者之前交易次数和新的交易收益,并且满足υ1+υ2=1。如果前交易对手的收益Rold大于或等于观察到的潜在新交易对手Rnew的收益,则该银行继续与当前银行进行交易。如果不是这种情况,则新银行以proD的概率替换之前的交易银行。

2.3 中央对手方

中央对手方在衍生品市场中充当每一个买方的卖方以及每一个卖方的买方,进而对交易对手间的衍生品合约进行干预。追加保证金是根据同业拆借利率波动而对金融机构进行流动性资产的追加担保,通常是在一天内完成[20]。当同业拆借利率剧烈波动时,金融机构需要提供大量的流动性资产作为担保,就有可能造成金融机构和金融市场的流动性风险。中央对手方通过多边净额结算的方式可以有效降低整个衍生品市场的风险敞口和追加保证金数量[5]。因此,本文在衍生品市场中考虑中央对手方的作用。本文在计算追加保证金时,借鉴了Vuillemey 和Breton 的方法[44]。但不同在于:Vuillemey 和Breton 是通过风险资产获得收益的概率的变化计算追加保证金,而本文则根据同业拆借利率的实际变化计算银行需要缴纳的追加保证金。实际中,追加保证金反映了衍生品交易标的物价格或利率变化导致的名义价值的变化。因此,本文的这种计算方式更加符合实际情况。中央清算存在时,银行的追加保证金通过多边净额结算的方式计算。因此,中央清算存在和不存在时,银行i对中央对手方和银行j的追加保证金数量分别为:

遵循买入看涨,卖出看跌规则。wij为正值表示银行i为空头,银行j为多头,当利率上涨时,银行i则需要付给银行j追加保证金。ρ为中央清算比例。只有卖方才会支付追加保证金,中央清算中心不向银行支付追加保证金,银行i支付的追加保证金为银行i对银行j和中央清算中心的保证金之和。此外,通过中央对手方进行衍生品交易的银行会缴纳相当于其初始保证金一定比例的违约基金给中央对手方,设置违约基金比例为0.1。中央清算存在条件下的风险敞口为∑i|∑jρNij|+∑i∑j |(1-ρ)Nij|。本文不考虑中央对手方违约,通常情况下,中央对手方违约概率极低,并且金融危机中政府往往作为最后贷款人,以防止中央对手方违约对整个金融系统产生冲击。

2.4 银行投资决策机制

2.4.1 预测策略

关于银行对预期收益的预测,本文采用了Wolski 和van de Leur 的方法,Wolski 和van de Leur 将预期收益的预测规则分为适应预测规则(ADA) 和趋势预测规则(TF) 两种[10,47]。适应预测规则表示个体认为市场利率会回归到基本利率水平,对利率的预测是由过去时期所有利率的平均值和上一时期对利率的预测决定:

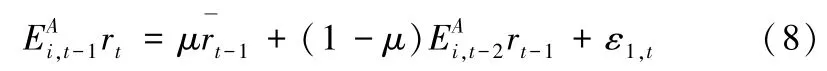
其中,ε2,t为服从N(0,δ2) 的误差项,g(rt-1-rt-2) 表示下一时期的利率预测会受到之前时刻的影响,并且g∈(0,1)。在初始时刻一半个体选择适应预测规则,一半个体选择趋势预测规则。在下一周期,银行根据预测误差的平方在预测规则之间进行转换。预测误差的度量为:

其中,τ∈[0,1]表示记忆参数,则改变策略的概率为:

φ＞0 表示选择强度参数,该参数决定银行选择性能更好的预测规则的速度。

2.4.2 资产分配

每个时期,每家银行会对不同市场的收益预期进行预测,基于投资组合理论,得到在不同市场的最优投资组合策略。对于在不同市场的具体投资额度,本文是采用Campbell和Viceira 提出的最大化改进的常数相对风险厌恶(CRRA)效用函数计算得到的[48]。

其中,xt=表示每个市场的投资比例,分别为债券市场、同业拆借市场、衍生品市场、证券市场和其他投资市场。每个市场的分配比例满足x∈[0,1],在同业拆借市场满足[-1,0]≤xI≤1,表示可以通过同业交易借入资金和借出资金。此外,银行在进行投资时,要同时满足流动性和资本监管要求①巴塞尔协议Ⅲ提出了流动性覆盖率(LCR),由于LCR 不容易量化,为了体现流动性监管要求,本文设置流动性资产比例为储蓄、同业负债、衍生品负债和其他负债总和的一定比例,流动性资产为现金资产。资本监管要求通过对不同资产的风险加权计算得到:,其中,Rei 和分别表示净资产和最低资本充足率。。由于同业拆借利率是债券利率加上风险溢价得到,对同业拆借利率的预测实际上是对风险溢价的预测。rt=表示五个市场利率或收益和同业拆借市场利率波动,圆圈表示哈达玛乘积。η表示风险规避程度,η=(ηs,ηl,ηl,ηl,ηl) 表示不同市场的投资周期,ηs和ηl分别表示短期投资和长期投资的风险规避程度,ηs∈[ηmin,ηmax],ηl=ξηs/2 表示不同投资周期风险规避程度的关系,本文中除债券市场周期为1 个时期,其他市场周期均为3 个时期。∑表示五个市场投资收益和利率波动率的方差-协方差矩阵,矩阵中的每一个元素可以表示为:

其中,θ∈(0,1) 表示记忆参数。

2.5 风险传染路径和模型演化过程

2.5.1 风险传染路径

银行多层网络中风险传染过程如图2 所示。在同业拆借市场,通过同业拆借关联,债权银行为了获得流动性会进行流动性囤积,提前收回同业贷款,进而造成债务银行的同业资产减少。债务银行破产无法偿还同业借款,也会对债权银行的同业资产产生影响。在衍生品市场,通过衍生品交易关联,同业利率的波动会导致期权卖方向中央对手方或买方支付一定的追加保证金,进而增加了卖方银行的衍生品负债。同时,合同到期时,如果买方行使期权,则会降低卖方银行的收益,衍生品交易对银行资产负债表的影响随着同业利率波动的增大而增大。在证券市场,通过持有共同资产关联,银行会通过抛售证券资产获得流动性,证券抛售导致资产价格下跌,其他持有相同证券资产银行的证券价值减少。在其他投资市场的投资可能会因为亏损而导致其他投资资产减少,向中央银行的借款则需要支付高额的利息。同业拆借交易关联和衍生品交易关联是直接风险传染渠道,持有共同资产关联是间接风险传染渠道。银行在不同金融市场的风险通过不同路径对银行资产负债表产生影响,当银行无法偿还债务、满足流动性和资本监管要求以及净资产为负时,则银行破产。

图2 银行动态多层网络模型风险传染过程Figure 2 Risk contagion process of bank dynamic multilayer network model

2.5.2 模型演化过程

在每个时期的开始,银行观察上一时刻不同市场的利率,根据预测误差选择预测策略,并进行储蓄①为了便于资产负债表处理,每个时期储蓄规模为净资产的倍数Dep 加上随机噪音N(0,σdep),储蓄到期返还给储户并支付无风险利率的利息。假设存在储蓄保险计划,短时间内大量储户提取存款而导致银行出现流动性短缺的概率极低。更新。债券以及部分证券和投资到期后,其中,相应收益添加到净资产中,相应的成本和收益添加到现金中,资产负债表的净资产和现金进行了更新。

在下一步,银行根据同业交易和衍生品交易的收益和损失更新资产负债表。银行首先用他们的现金来偿还部分同业债务、中央借款利息、追加保证金、衍生品债务以及满足流动性和资本监管要求。当现金不足以偿还债务和满足监管要求时,银行会通过流动性囤积,即提前收回同业贷款,同业贷款按比例分配给借款银行。而同业贷款也不足以满足上述要求时,则会通过抛售证券资产获得流动性,同时抛售证券会导致资产价格变化②证券抛售会导致证券资产价格下跌,参照Cacciolietal.(2014)的研究,证券抛售数量与资产价格关系为:pt+1=,α=1.0536 表示证券抛售数量与价格变化近似为线性关系[49]。,如果证券被全部抛售到总资产等于总负债时,并且抛售数量不能超过持有的证券资产数量,仍不能抵扣借款和追加保证金以及满足监管要求,则该银行破产。这时,如果该银行从多个交易对手那里借入资金时,偿还金额将按比例分配给债权银行,相应的债权银行由于不能完全收回资金而遭受资产损失。证券抛售引起资产价格下跌,会导致其他所有持有该证券的银行的证券资产价值减少。如果银行净资产为负,则该银行破产。同时,一家资产负债表规模为0.8～1 的银行替换该破产银行。

下一阶段,银行根据预测规则对不同市场的利率和风险溢价进行预测,在保持流动性监管要求的基础上,根据最优组合理论选择最优的投资组合配置。假设债券、证券和投资项目供应量没有限制,然后通过上述交易规则实现银行在同业拆借市场和衍生品市场的交易。如果在同业交易和衍生品交易结束后一家银行在同业拆借市场或者衍生品市场分配的资金仍有剩余,那么剩余的资金就会按比例投资于证券、债券和投资市场,这个比例为当期确定的投资比例;如果借款银行在同业市场上的流动性需求未得到完全满足,会以较高的利率rC向中央银行借钱,并作为该银行的同业资产,同时添加到其他负债中,实际同业拆借利率为所有同业交易的加权平均。在衍生品市场,卖出衍生品合同获得的资金为衍生品收益,衍生品合同买方根据到期时同业拆借利率波动决定是否行使期权。一般情况下,买方为衍生品资产方,卖方为衍生品负债方,并对资产负债表进行更新,所有资产负债表变量将被存储并进入下一个周期。

3 结果分析

本文构建的经济系统包括100 家银行,并根据我国实际经济情况以及参考相关文献对模型参数初始值进行校准,如表2 所示。债券利率参照2002—2019 年我国十年国债收益率的平均水平,债券利率标准差设置为10 bp,表示无风险利率水平。参照《商业银行资本管理办法》,银行最低资本充足率设置为8%,同业资产、衍生品资产、证券资产和其他投资资产的风险权重分别为20%、100%、100%和100%。根据惠誉评级发布的《中国企业债市场蓝皮书》,银行违约概率设置为满足贝塔分布Beta(5,1000),银行平均违约概率与2014—2019 年中国企业违约概率平均值相一致。其他投资收益最大值设置为债券利率的两倍,其他投资收益最大标准差设置为介于证券收益波动最小值和最大值之间,表示投资项目较高的收益和风险水平。存款净资产比率根据近五年我国主要商业银行存款与净资产比值的平均值得到。交易对手匹配权重均为0.5,表示假定之前交易次数和交易利率或交易收益对银行更换交易对手概率的影响同样重要。初始保证金比例为1,通过改变初始保证金比例分析保证金制度对银行系统的影响。流动性水平参照文献[49]设置为1.0536,表示证券抛售数量和价格变化近似为线性关系。证券收益波动、风险规避程度和流动性资产比例分别参照文献[45]、[50]和[51]进行设置。折扣因子、中央借款利率、方差协方差矩阵记忆参数、初始方差协方差矩阵标准差以及预测规则的相关参数与文献[10]保持一致。初始时刻所有银行的资产负债表均为1,在初始时刻一半个体选择适应预测规则,一半个体选择趋势预测规则[10]。在下一周期,银行根据预测误差的平方,在预测规则之间进行转换。在初始的前三个周期内,没有同业拆借和衍生品交易,银行在满足流动性监管要求后将剩余现金按照最优投资组合理论投资于债券、证券和投资三个市场。初始时刻的方差协方差矩阵的每一个元素服从均值为0 方差为h的正态分布。本文首先分析巴塞尔协议III 的流动性监管和市场约束的宏观审慎监管对银行系统的影响;然后结合上述监管约束和货币政策,分析宏观审慎和货币政策双支柱以及单独货币政策对银行系统的影响;最后从衍生品市场的角度分析保证金制度和中央清算机制对银行系统的影响。

表2 参数设置Table 2 Parameter setting

3.1 宏观审慎监管

2007—2009 年的金融危机直接催生了巴塞尔协议Ⅲ。与前两部相比,巴塞尔协议Ⅲ提出了流动性覆盖率的概念,以提高银行应对流动性风险的能力,并通过逐年提高流动性覆盖率的方式达到流动性覆盖率要求[1]。同时,引入了市场约束机制,要求银行提高资产信息的透明度,及时披露资本结构、风险敞口等,以降低信息不对称带来的系统性风险。在市场约束条件下,市场信息完善,银行能够准确知道系统中其他银行的资产相关信息,并且通常会选择净资产较大的银行进行交易以降低交易对手银行违约对自身造成的资产损失。因此,本文将银行的流动性资产比例设为15%,以反映更严格的流动性监管要求,并假设银行在进行同业和衍生品交易时,会优先选择资产净值较大的银行进行交易,以分析流动性监管和市场约束机制对银行系统的影响。运行周期为500,结果为运行50 次的平均值,如表3 所示。

表3 监管前与监管后对比Table 3 Comparison between pre-regulatory and post-regulatory

表3 结果为500 个周期的平均值。从表3 可以看出,提高流动性监管要求使得银行将更多的资金留作储备,用于投资的资金减少,进而减缓了银行扩张速度,导致银行资产总规模降低。中央借款规模的降低反映了同业拆借市场规模的萎缩,银行对债权方银行和中央银行的负债减少。流动性资产比例的增加使得银行有充足的资金偿还同业、追加保证金以及衍生品等负债,减少了证券的抛售比例,缓解了证券的大量抛售对银行资产价值下跌的影响。在市场约束条件下,银行优先与风险水平较低的银行进行同业和衍生品交易,降低了银行系统的逆向选择风险。同时,衍生品市场风险敞口的减少也在一定程度上减少了违约银行的数量。这一结果表明,对银行系统更高的流动性监管要求和市场约束要求虽然在一定程度上抑制了银行系统的发展,但同时也降低了银行系统的风险水平。

3.2 宏观审慎监管和货币政策工具

公开市场操作、存款准备金率和直接注资等是当前金融市场调节最常用的货币政策工具,央行通过实施货币政策工具来调节货币供给和市场流动性以达到降低金融系统性风险和保持金融系统稳定运行的目的。由于债券利率作为基准利率,债券市场的变化往往会对其他金融市场产生影响。本文通过改变债券利率、债券利率波动率γB和市场流动性水平α的参数值来模拟不同情境下,宏观审慎监管政策和货币政策结合以及单独货币政策条件下,整个银行系统的变化情况。输出结果包括银行平均总资产、破产银行数量、证券抛售比例、中央借款、衍生品风险敞口和追加保证金数量。运行周期为500,结果为运行50 次的平均值,如图3～图5 所示。

图3 债券利率敏感性Figure 3 Bond interest rate sensitivity

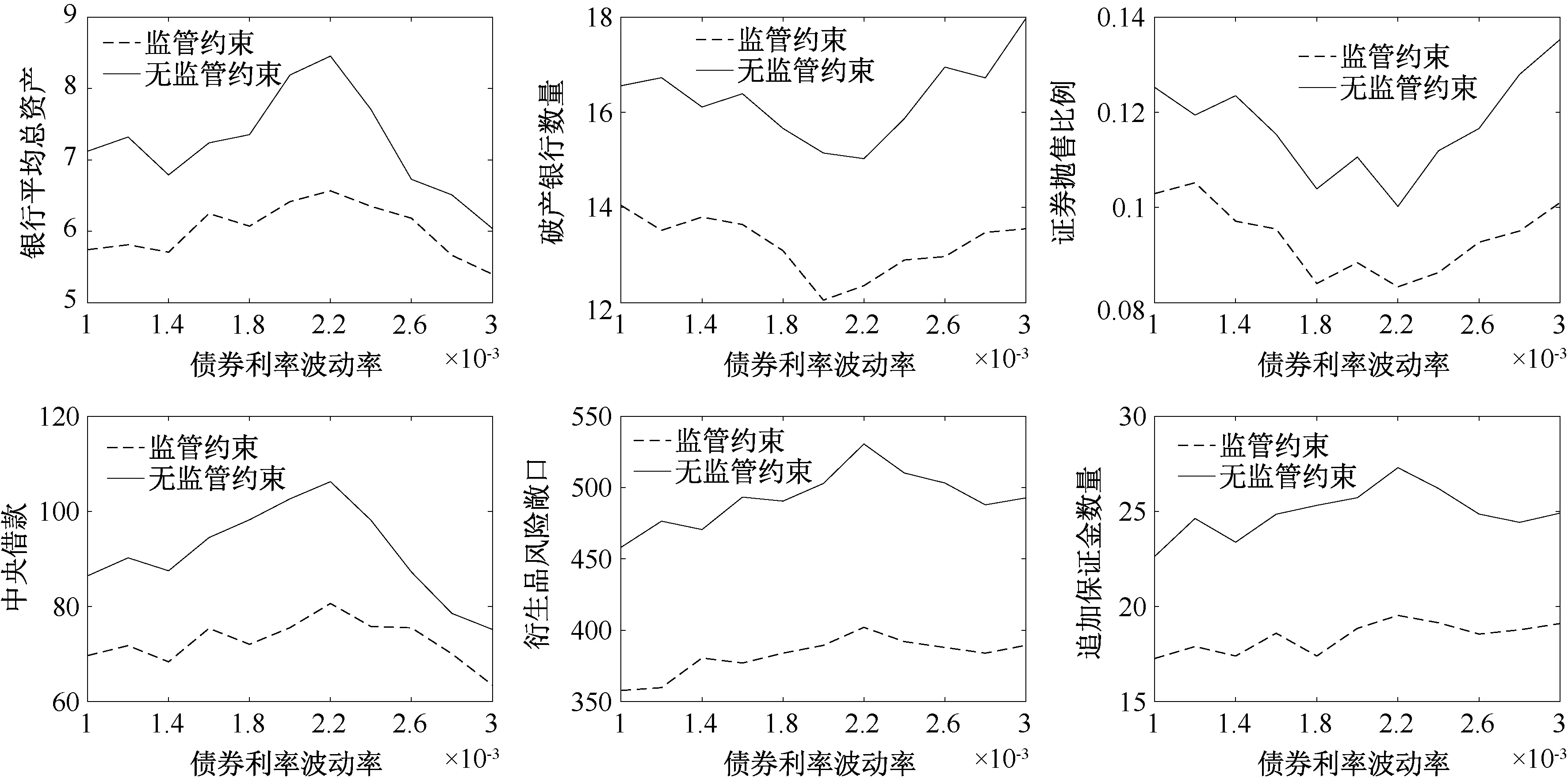
图4 债券利率波动率敏感性Figure 4 Bond interest rate volatility sensitivity

图5 市场流动性水平敏感性Figure 5 Market liquidity level sensitivity

债券利率的变化对银行系统产生了显著的影响,图3 中较高的债券利率增加了银行现金和净资产规模,同时银行资产规模呈上升趋势。较低的债券利率水平传导到同业拆借市场,导致流动性供给降低,银行从中央借款规模增加。因此,在较低的利率水平下,中央借款规模保持较高水平。银行资产规模的增加,使得中央借款规模和衍生品风险敞口增加。同时,较高的债券利率也会对同业拆借利率产生影响,进而导致追加保证金规模增加。中央借款和追加保证金的增加,使得很多银行的流动性资产可能不足以偿还负债,不得不通过抛售证券进行偿还,而证券抛售又进一步恶化了银行的资产负债表,违约银行数量也相应的增加。在宏观审慎监管约束下,证券抛售比例、追加保证金和违约银行数量等均小于没有监管约束,并且债券利率的变化对银行系统的影响显著降低。

图4 中债券利率波动率的增加,导致债券市场风险增加,银行资产从债券市场向同业、证券和投资等收益更高的市场转移,进而使得总资产规模增加。但当波动率增加到一定程度时,银行资产规模呈现下降趋势,说明一定程度的债券利率波动有利于银行系统的稳定发展,但过高的债券利率波动反而会降低银行系统的稳定。受债券市场利率波动的影响,同业拆借市场利率波动也随之增加,为了对冲同业拆借利率波动带来的风险,银行会增加对衍生品市场的投资,造成衍生品市场风险敞口的增加。此外,同业拆借利率的波动也引起了追加保证金数量的大幅增加,证券抛售比例和违约银行数量也随之增加,进而增加了银行系统性风险,导致银行资产规模降低。通过对银行平均资产规模、证券抛售比例和违约银行数量的对比,可知宏观审慎监管约束降低了过高债券利率波动对银行系统的负面影响。

图5 反映了市场流动性水平变化对银行系统的影响,横坐标为参数α值,α越大表示市场流动性水平越低。可以看出,市场流动性水平的增加,能有效的降低银行系统性风险水平,主要体现在证券抛售比例和破产银行数量的减小。可以理解,较高的市场流动性水平有效吸收市场中抛售的证券,抑制了证券价格的大幅下跌,降低了证券抛售对银行资产负债表的影响。同时,较高的流动性水平也降低了流动性风险对同业拆借市场的影响。当市场流动性水平较低时,市场流动性水平对银行系统的负面影响显著增加,流动性水平越低,市场对抛售证券的吸收能越差,证券抛售会导致资产价格的大幅下跌。部分银行由于净资产小于零而破产,对其债权银行造成资产损失,债权银行为了偿还负债又会进一步抛售证券,违约级联效应导致证券抛售比例大幅上升。同时,破产银行数目增加。

3.3 衍生品市场监管

衍生品市场监管主要体现在保证金制度和中央清算机制。通过对衍生品交易双方设置保证金制度以降低衍生品资产价格波动带来的交易对手风险,中央清算机制则是中央对手方充当每一个买方的卖方以及每一个卖方的买方,通过多边净额结算的方式降低整个衍生品市场的风险敞口。本文分别通过改变初始保证金比例β和中央清算比例ρ的参数值来分析保证金制度和中央清算机制对整个银行系统的影响,结果如图6 和图7 所示。

图6 初始保证金比例敏感性Figure 6 Initial margin ratio sensitivity

图7 中央清算比例敏感性Figure 7 Central clearing ratio sensitivity

图6 中较高的初始保证金比例增加了衍生品交易成本,导致衍生品交易规模的萎缩,相应的衍生品风险敞口和追加保证金也降低了。同时,证券抛售比例和破产银行数量呈下降趋势。大量研究验证了中央对手方在降低衍生品市场风险中的作用,图7 中的结果也表明,对衍生品交易实施中央清算能够显著降低银行系统性风险。随着中央清算比例的增加,通过对所有衍生品交易的多边净额结算,衍生品市场风险敞口和追加保证金均逐渐降低。对比图6 和图7,可以看出,与保证金制度相比,中央清算机制在降低银行系统性风险中的效率更高。

4 结论

本文构建了银行动态多层网络模型,包括同业拆借网络、衍生品交易网络和持有共同资产网络,同时考虑直接和间接两种风险传染渠道。衍生品市场对银行系统稳定具有重要影响,以往对银行系统性风险监管的研究往往忽视了衍生品市场在整个金融系统中的作用,将衍生品市场纳入到整个金融系统中,可以较为准确全面的分析不同市场间的相互作用所呈现出的宏观特征。基于构建的模型,本文通过参数设置模拟了宏观审慎监管和货币政策工具对整个银行系统影响,研究结果如下。

更高的流动性监管要求和市场约束要求虽然在一定程度上抑制了银行业的发展,但同时也降低了银行资产过度扩张带来的系统性风险,有利于维持银行系统的稳定。建立完善的信息披露机制能够充分发挥市场约束机制的作用,减轻银行交易的逆向选择风险。虽然较高的流动性资产比例能够有效抵御外部冲击,降低银行系统性风险,但过高的流动性资产比例会造成资本冗余,导致资本效率低下。因此,应该有针对性的实施监管策略。巴塞尔协议Ⅲ中也确定了系统重要性金融机构,这些金融机构的违约能够对整个金融系统产生严重影响,并对系统重要性金融机构提出了附加资本的要求,以避免系统性风险的发生。

债券利率及其波动均会对银行系统产生显著影响。紧缩的货币政策导致市场流动性水平降低,流动性风险增加,银行为了获得流动性资金通过流动性囤积、出售证券以及支付高额利息向中央银行借款,从而进一步恶化了银行的资产负债表,很多银行由于不能及时支付借款而破产,并引发银行系统的连锁反应。较低水平的债券利率波动有利于银行系统的稳定发展,但过高的波动会对银行系统带来负面影响。债券利率波动传导到同业拆借市场,银行会通过增加衍生品投资以降低同业拆借利率波动带来的资产损失,导致风险敞口和追加保证金的大幅增加,降低了银行系统的稳定性。市场流动性水平对银行系统具有重要影响,央行一般会通过直接注资、公开市场操作以及准备金率等来调节市场流动性水平,但货币政策的效果并不是针对单一市场,不同市场间会相互作用对整个金融系统产生影响。在市场流动性水平低于一定程度时,市场流动性水平对银行系统的负面影响会显著增加。过于频繁的政策操作会降低银行对市场前景的预期,增大了利率的波动和市场的不稳定性,进而对银行系统产生影响。可以综合运用宏观审慎监管政策和货币政策工具,以降低不同市场间相互作用所导致的风险放大效应,保持银行系统的平稳运行。

保证金制度和中央清算机制在降低衍生品市场风险中具有重要作用。初始保证金通过增加交易成本,降低了衍生品交易规模,进而降低衍生品风险敞口,较高的初始保证金比例也促使更多地场外衍生品交易通过中央对手方进行。中央对手方通过多边净额结算的方式将不同交易对手间的风险集中到中央对手方身上。与双边结算方式相比,多边净额结算降低了对交易双方的保证金要求,进而降低了流动性风险,但这也增加了极端情况下中央对手方的违约风险,可以通过适度提高初始保证金和违约基金的缴纳比例以应对极端情况。

对于银行系统性风险,本文重点研究了同业拆借交易和衍生品交易的直接风险传染渠道,以及持有共同资产抛售导致资产价格下跌的间接风险传染渠道。而银行股价波动也是银行系统性风险的重要来源之一。银行股票价格受宏观经济环境、政策干预以及银行自身经营业绩等多种因素影响,银行股票价格的波动会对银行资产负债表产生影响。银行股票价格上升会优化银行的资产负债表,有利于增强银行风险抵抗能力;股票价格下降会恶化银行的资产负债表,会造成银行更加脆弱。同时,银行资产负债表的变化也会反过来对股票价格产生影响[52]。因此,纳入股票市场研究银行系统性风险值得未来进一步深入研究。