基于自组织映射网络的电力最短巡检路径问题求解

倪 俊，李 锋，赵 芳，韩明冲，钟建伟

（1.国网湖北省电力有限公司恩施供电公司，湖北 恩施 445000；2. 湖北民族大学 信息工程学院，湖北 恩施 445000）

0 引 言

伴随着我国经济的快速增长，社会各方面的发展对于电力供应的可靠性提出了更高的要求。电力系统运行过程中，需要对其线路上的各种电力设备进行定期巡检，以保证电力系统运行的可靠性。在以往进行电力巡检时，普遍采用人工巡检的方式，但随着人们对于电力供应方面需求的提升，巡视效率就急需进一步提升，同时还应尽可能降低进行相关工作时的成本。从全局优化的角度出发，对输电网络中的最优化巡检方案进行分析，并通过有效的巡检方案的制定提升电力资源的配置能力。电力巡检可分为常规巡检、临时巡检以及保障巡检三方面。其中常规巡检主要是管理人员通过获取方案的第一手资料，进而对其线路中的变电站、架空线、电杆以及杆上的设备进行整体性巡查。在此过程中需要配备专业人员对其路径的选择进行合理的规划，但在进行巡检车辆的调遣过程中需要充分依靠巡检人员的工作经验，故此工作的开展具有较大的主观性。现阶段，为了能进一步提升电力巡检效率，需要集合电力巡检实际业务特征对其进行抽象化分析；并结合当地实际线路巡检需求，得出相应最优化电力线路的巡检路线。而巡检的最短路径问题可以简单看作旅行商问题（Travelling Salesman Problem, TSP）。TSP可被简单描述为已知某一地区上的地点以及各点之间的距离，求出遍历所给地点的最短路径。虽然该问题描述起来很容易，但它是一个NP完全问题。地点数目越多，求解难度越大，并且这类问题没有通用解法。由于现在基本很难验证当地点数量过多时模型求得的解是否最优，所以目前认为任何次优解都是足够好的。本文利用SOM解决TSP问题，将地点的二维坐标作为网络的输入，将地点位置之间的关系作为其学习模式，而其输出则是一个环形结构。

1 自组织映射

1.1 基本原理

1981年学者TeuvoKohonen从人类大脑中神经元自组织和侧抑制现象中寻得了灵感，并结合无监督学习的方法提出了自组织映射网络（SOM）的概念。SOM的结构主要由如图1所示的输入层、输出层（特征映射）以及全连接（权值矩阵）组成。

图1 SOM结构

大脑皮层分为很多区域。对于外界的刺激，大脑皮层根据刺激种类使不同的区域发起反应。与之类似，SOM会根据其所接受到外界不同的输入模式选择不同的应对区域并作出不同的响应。所涉及分区的对应关系是在不断的训练学习中明确的。另外，生物的神经元间有着侧抑制现象：其他神经元离自身较远则相互抑制，反之则相互激励。这些神经元中对刺激响应最强的称为获胜神经元，以获胜神经元为中心向周围辐射一个范围，距离越近则激励越强，反之越弱。激励作用示意图如图2所示。

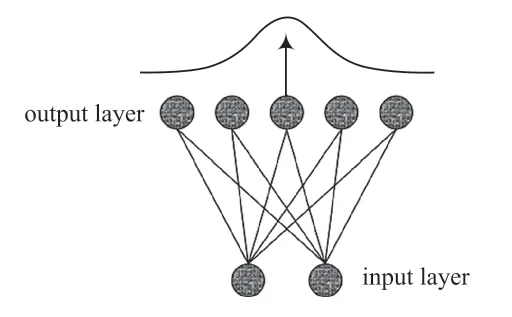
图2 激励作用示意图

上述提及的范围在SOM中被称为优胜邻域，这种范围可以促使周围神经元兴奋。SOM有两层神经网络，分别是输入层（IL）和输出层（OL）。网络中的OL一般为一个二维神经元网格，而代表现实世界中模式的数据作为IL的输入，SOM的任务就是将输入数据的模式在OL中映射出来。在模型训练过程中，OL神经元中的权值向量会不断更迭变化，从而使得OL神经元“学会”输入至IL中数据所蕴含的模式。对旅行商问题而言，将地点的二维坐标作为网络的输入，将地点位置之间的关系作为其学习模式，而其输出则是一个环形结构。

进行训练时首先应选择出获胜神经元，选择依据就是输入向量和神经元权值向量之间的相似程度。之后根据式（1）对获胜神经元附近的神经元权值向量进行更新，从而使其值逐渐接近IL的输入向量与获胜神经元的权值向量。

式中：n和n+1分别为更新前和更新后的神经元；为获胜神经元对其优胜邻域内的神经元作用大小的邻域分布；为神经元距离其附近获胜神经元的长度。

近邻神经元为处于获胜神经元优胜邻域中的神经元，用表示两种神经元间的距离，则获胜神经元对其近邻神经元的作用强弱近似为正态分布。

优胜邻域如图3中所示气泡部分，气泡外的神经元则不会更新，而气泡内的神经元将会更新。当OL神经元的排列情况为二维网格状时，属于优胜邻域这个“气泡”内的神经元的权值向量值将会得到更新。

图3 近邻神经元

图4为SOM训练过程的示意图。训练数据的分布情况用阴影表示，从该分布中选出目前的训练数据并用白色斑点表示。首先如图4左侧部分随机在数据空间中定位SOM节点，然后将最靠近训练数据的节点定为获胜节点并将其标记。该节点网格上的相邻节点与其自身将逐步向训练数据移动，多次迭代后结果如图4中右侧图所示，网格已接近数据的分布。

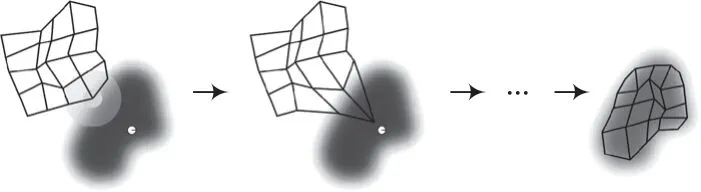
图4 自组织映射训练示意图

1.2 利用自组织映射解决旅行商问题

由式（1）已知神经元的更新方式，下一步还须明确哪一个神经元为获胜神经元。首先应测出输入向量与神经元权值向量之间的欧氏距离，若与某一神经元距离最小，则说明两者之间最接近，将其定为获胜神经元。由于本文对于SOM模型的输入数据为地区地点二维坐标，所以地图中地区地点应与获胜神经元的位置最为接近。

在每次训练过程中获胜神经元与其近邻神经元的权值向量都将不断更新变化，SOM经过足够次数的竞争，会逐渐学会输入数据的模式，在本应用中即为地区各地点之间的空间关系，这种关系将会被保存为神经元权值向量的形式。图5为路径计算过程示意图，神经元和地区地点分别用圆圈和正方形表示，神经元不断接近地区的地点直至与其重合，最后形成的环状结构就是利用SOM所求得的最短路径。

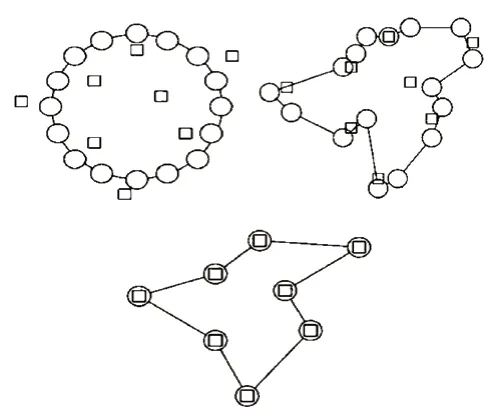
图5 路径计算过程

将SOM应用于TSP问题的关键在于优胜邻域的调整。本文将SOM的OL神经元排成环形阵列的形式，使每个节点只与其前后的两个神经元进行竞争。然后SOM的输出路径一边控制路径总长，一边向地区地点靠近，最终得到一条最短的路径。

本文的SOM算法因在时间上不会自动进行收敛，但又需要算法不断地对优胜邻域进行调整，所以需要设置学习率，用控制算法模型的探索过程以保证模型良好的收敛性。同时，还需要让和邻域值随着时间而衰减，以达到模型探索充分的目的。前者会使模型计算过程收敛，后者能使离地区地点相对较远的神经元也加入探索的过程。将算法收敛考虑进去，模型OL神经元的权值将按式（2）进行更新。

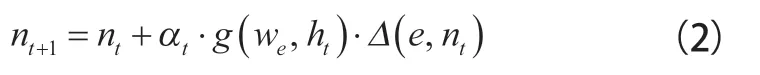
式中：为学习率；为获胜神经元的优胜邻域，它是以更新前的优胜邻域为标准差，同时以获胜神经元作为中心的高斯函数。

式（3）和式（4）分别表示学习率和优胜邻域随时间衰减。

其中，γ和γ分别为学习率和邻域值的衰减率。

对SOM模型设置初始的优胜邻域和学习率以及两者各自所对应的衰减率，之后按上述步骤运行。优胜邻域和学习率都会随着模型的不断迭代而减小，最后收敛。

将某一地区地点与其相应的获胜神经元连接起来，随机选择一点开始，然后按照获胜神经元的顺序对地区地点排序。另外，若SOM没有考虑穿越某些地区地点的顺序，或者因为穿越顺序与总距离的相关性太低，又或者因为精确度太低，以至于在这个过程中可能会出现若干个地区的地点映射到了同一神经元的情况。这时就需要考虑这些地区地点的各种可能的排序情况。

2 实例研究

2.1 仿真条件

本文实验程序采用Python语言编写，所编写程序于PyCharm软件Python3.8环境下进行。实验数据源自如图6所示的滑铁卢大学在“National Traveling Salesman Problem instances”项目中的数据库，其中的数据包含地区地点的位置以及目前得到的最短路径。

图6 实验数据来源

另外，评估过程中对所用的参数做了调整。首先，SOM网络规模（神经元数量）是地区地点总数的8倍；其次，初始学习率设置为0.8，衰减率设置为0.999 97；最后，初始优胜邻域值为地区地点总数，且将衰减率设置为0.999 7。

2.2 实验结果

对于SOM模型中的某些参数本文设置了阈值，在计算过程中若其参数数值低于本文所设置的有效阈值时，模型将停止迭代并输出结果。虽然SOM模型可以为实验选取的五个实例寻到更精确的参数，但本文还是采用了统一的方法对这五个地区进行了测试。表1为使用模型对每个实例计算五次所得的数据。

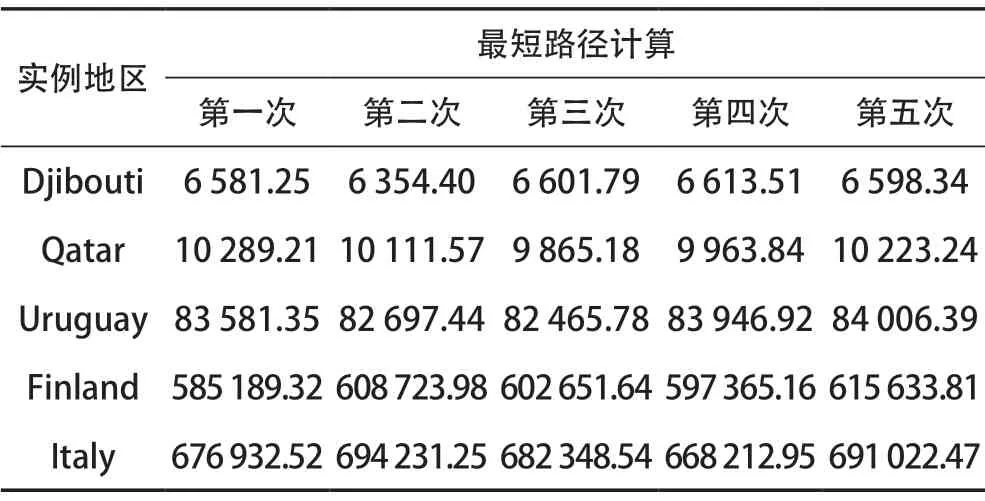
表1 实例计算数据

图7为对卡塔尔地区194个地点的最短路径计算分别迭代1 000、5 000、11 000次以及最终的输出情况。

图7 卡塔尔地区路线变化情况

表2中的运行结果是对每个实例计算五次后去掉最大和最小数值后所求取的平均值。

表2 实例数据详情

从表2中的数据可以发现，模型运行时间随着地区地点数目的增加而增加。除了Uruguay地区外，当地区地点数目较低时，误差通常会更小；反之，误差将会变大。但Uruguay地区比Qatar地区多了五百多个地点，其误差反而更小，猜测Qatar地区总距离和穿越顺序的相关性不高，因此对计算的精度有了影响。

3 结 语

电力巡检过程中的巡检点可以近似看作TSP问题中的地点。为求出各地点间的最短路径，提高电力巡检效率，本文将SOM应用于该问题中，并通过五个地区的实例验证了该方案的可行性。实验数据表明，该方法收敛速度较快。同时，当地点数目较少时模型计算结果误差较小，反之则较大。又因巡检任务中的巡检点数量一般不会太多，所以使用该模型求解电力巡检最短路径问题有着较高实用价值。