基于改进布谷鸟算法的配网故障定位研究

李梦媛，史 辉，宋艳争

(国网冀北电力有限公司技能培训中心，河北 保定 071051)

近年来，随着居民用电量的大幅上升，以及受天气、环境、配网线路老化等影响，配网故障频发，如何保障居民用电的稳定性成为电力领域思考和研究的重点。由于配网网络结构复杂，且配网运行影响因素较多，因此给故障的定位带来不便。目前常用的配网故障定位方法有阻抗法、行波法等。杨定乾等[1]提出了基于扫频阻抗法辨识的电力变压器绕组变形智能检测技术；柴鹏等[2]基于双端行波法实现了对电缆线路短路故障的定位。虽然上述方法可实现配网故障定位，但不能对伪故障点进行判断，且故障定位精度低。由此人们引入智能算法对配网故障进行定位，如王禄海等[3]基于Fibonacci搜索对含DG配网故障进行定位；蔡朕、陈磊等[4-5]提出了改进矩阵算法和灰狼算法对配网故障进行定位。由以上研究可以看出，进行智能化配网定位成为当前的趋势。本文基于布谷鸟算法的特点，提出一种改进布谷鸟算法的配网故障定位方法，以期在提高定位精度的同时，为配网定位提供新的可借鉴的方法。

1 基本算法与改进

1.1 布谷鸟算法

布谷鸟算法是一种模拟布谷鸟寄生育雏特点和利用Le'vy飞行搜索机制解决最优化问题的搜索算法[6]。在布谷鸟算法中，一个鸟巢为一个候选解，N个候选解即组成了可行解空间。在可行解空间内，根据Le'vy飞行搜索机制，布谷鸟可依据式(1)寻求最优解的路径，并更新位置。

(1)

(2)

(3)

式中：μ，v为两个服从正态分布的随机数；β为飞行指数，β=1.5；Γ(·)为跳跃函数。

布谷鸟在进行Le'vy飞行中，随机搜索路径与飞行时间t1的关系如式(4)，服从Le'vy分布。

(4)

式中：λ为幂次系数。

1.2 改进布谷鸟算法

布谷鸟算法在搜索寻优过程中，利用Le'vy飞行大步长和小步长交叉使用的特点，可以实现在整个空间内高效寻优。但由于其更新步长大小的方式是依据Le'vy飞行机制随机变化的，由此导致寻优结果具有很大的随机性。如果步长较小，容易导致算法收敛速度缓慢，求解精度低；如果步长较大，容易导致算法忽略局部最优解，降低算法精度。故选择合适的步长有利于提高算法精度。

研究认为，步长和迭代次数相互影响，是影响算法全局搜索精度和局部搜索精度的两个关键因素[7]。本文结合步长和迭代次数对布谷鸟算法进行改进，具体改进思路是：设置较长的初始步长，由于较长的初始步长可加快算法迭代速度，实现全局优化，因此设置较长的步长有利于加快算法收敛速度；迭代到一定次数后，缩小步长，实现对向量解的微调，进而提高算法的搜索精度。当迭代达到一定次数后，算法得到的解越来越接近最优解，降低搜索步长，可提高算法全局寻优的准确性。

改进的布谷鸟算法步长计算公式为：

(5)

式中：r为步长控制量；iter为当前迭代数；NG为最大迭代数；Ub，Lb分别为变量的上限和下限。

2 基于改进布谷鸟算法的配网故障定位

2.1 编码方法

通常认为配网只有正常和故障两种状态[8]。针对闭环的多电源配网，故障状态又包括故障电流方向与电流方向一致和故障电流方向与电流方向相反两种情况。因此，根据上述描述，本文将多电源闭环配网故障状态编码如下：

(6)

式中：Ik为配网开关k的实际故障状态。

2.2 评价函数

评价函数即算法的目标函数。本文构建评价函数的目的就是求取目标函数的最小值。同时在实际故障预测中，由于配网中的智能配电终端上传的信息可能丢失，因此当评价函数取最小值时，可能对应多种故障状态，进而导致定位存在误差。为解决上述问题，引入最小集概念构建评价函数，具体为：

(7)

2.3 基于改进布谷鸟算法的配网故障定位流程

基于改进布谷鸟算法的配网故障定位流程如图1所示。

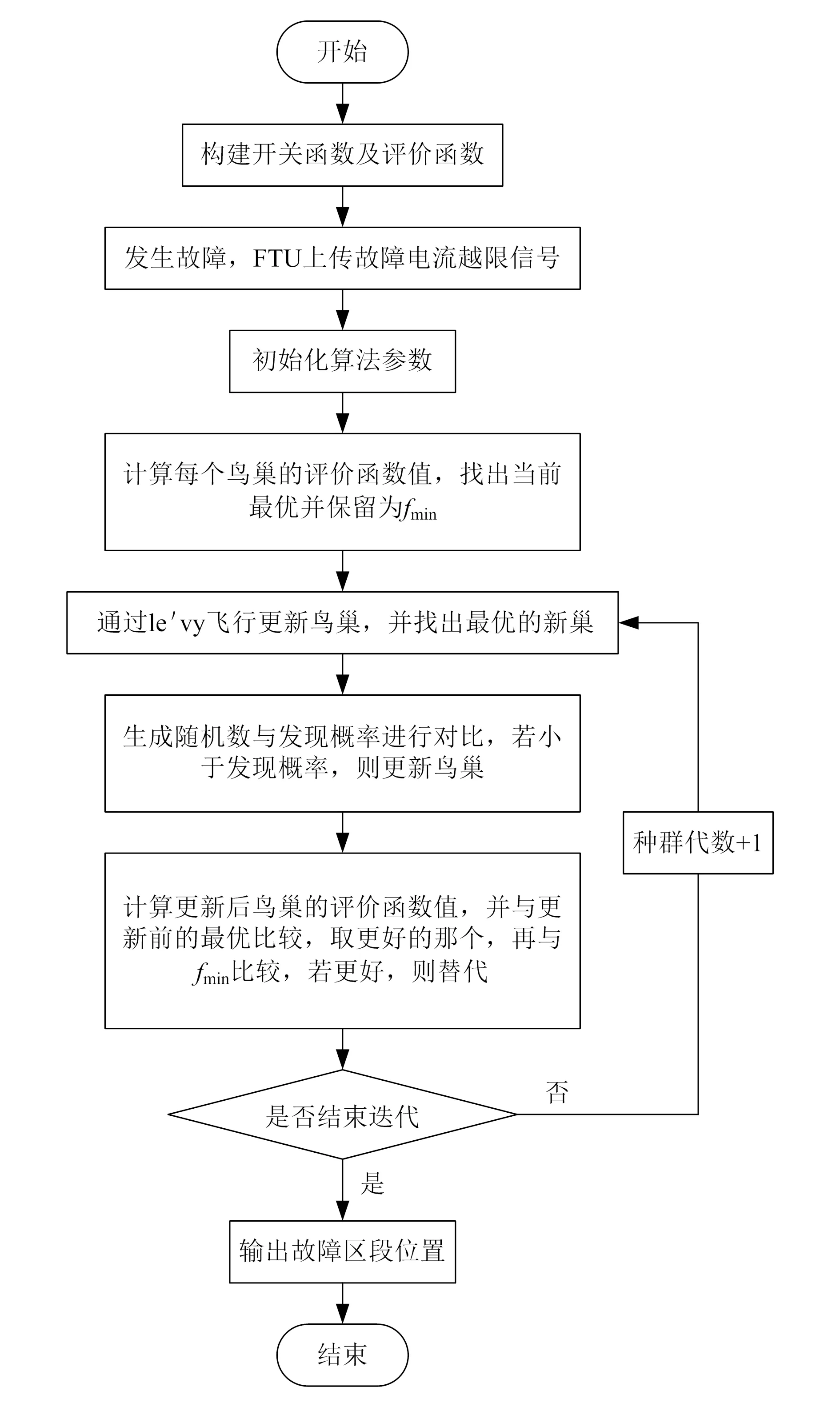
图1 基于改进布谷鸟算法的配网故障定位流程

3 仿真验证

3.1 改进布谷鸟算法性能验证

为验证改进布谷鸟算法的性能，设置种群大小为40，最大迭代次数为200，变量数为2，发现概率Pa为0.25，最优值保留代数为15。分别采用cross-in-tray函数、eggholder函数、holder table函数对改进前后的布谷鸟算法性能进行测试。

在进行50次仿真后，其平均最优值及标准差见表1。由表可知，在相同条件下，改进的布谷鸟算法求得的最优解优于标准布谷鸟算法，且该算法求得的最优解稳定性更好。

表1 布谷鸟算法改进前后最优解及标准差

3.2 多电源配网故障仿真

以某三电源配网为研究对象，其拓扑图如图2所示。图中，A、B、C为电源，KL1、KL2为联络开关，k1、k9、k15为进线断路器，其余为分段开关。设置单故障、双故障、三故障3种故障类型。设定改进布谷鸟算法种群数量为500，最大迭代次数为50，变量数为18，发现概率为0.2，变量上界为200，变量下界为0，最优值保留代数为25。

图2 三电源配电网拓扑图

3.2.1单电源故障定位仿真结果

假设KL1=KL2=1，x4区段出现故障，则配电开关监控终端(feeder terminal unit，FTU)上传到数据采集与监控(supervisory control and data acquisition，SCADA)系统每个开关的实际故障状态为Ik=[1 1 1 1 -1 0 0 -1 1 1 1 1 1 1 0 1 1 1 1]。由式(7)得到评价函数最优值为：

(8)

采用改进布谷鸟算法进行故障定位，得到如图3所示的结果。由图可知，评价函数值为0所对应的最优个体中值为1时，其对应的是x4区段，表明x4区段存在故障，与实际情况一致，说明基于改进布谷鸟算法的配网故障定位模型可进行单电源故障定位。

图3 单电源故障算法收敛图

3.2.2双电源故障定位仿真结果

假设KL1=0，KL2=1，x3和x11段同时出现故障，则FTU上传到SCADA系统每个开关的实际故障状态为Ik=[1 1 1 -1 0 0 0 -1 1 1 1 0 0 0 1 1 1 1]。由式(7)可得到评价函数最优值为：

(9)

用改进布谷鸟算法进行仿真定位，得到如图4所示的结果。由图可知，评价函数最小值为0.6所对应的最优个体中值为1时，其对应的是x3和x11区段，表明x3和x11区段存在故障，与实际情况一致，说明基于改进布谷鸟算法的配网故障定位模型可用于双电源故障定位。

图4 双电源故障算法收敛图

3.2.3三电源故障定位

假设KL1=KL2=1，x6,x12和x16区段同时出现故障，则FTU上传到SCADA系统每个开关的实际故障状态为Ik=[1 1 1 1 1 1 0 1 1 1 1 1 -1 0 1 1 -1 -1]。由式(7)可得到评价函数最优值为：

(10)

采用改进布谷鸟算法对故障定位进行仿真，得到如图5所示的结果。由图可知，评价函数最小值为1.2所对应的最优个体中值为1时，其对应的是x6,x12,x16区段，表明x6,x12,x16区段存在故障，与实际情况一致，说明基于改进布谷鸟算法的配网故障定位模型可定位三电源故障。

图5 三电源故障算法收敛图

3.3 算法比较

为验证改进布谷鸟算法定位的准确性，采用本文改进布谷鸟算法与标准布谷鸟算法、自适应遗传算法(adaptive genetic algorithm, AGA)对图3所示拓扑结构的配网故障进行100次仿真。仿真实验前，设置3种算法参数，设定种群数量都为500，最大迭代次数为100，最优值保留代数为10。改进布谷鸟算法变量数为18，发现概率为0.2，变量上界为200，变量下界为0；AGA算法交叉概率Pc1=0.9，Pc2=0.6，变异概率Pm1=0.20，Pm2=0.15，变量数为18。仿真结果对比见表2。

由表2可知，改进布谷鸟算法准确率均高于98%，且在多个故障定位中，准确率高达100%；标准布谷鸟算法准确率在93%以上，在T4类故障中的识别定位准确率为100%；AGA算法准确率较低，均在60%以下。由此可知，本文提出的改进布谷鸟算法在配网故障定位中具有更好的准确性，优于传统的标准布谷鸟算法和AGA算法。

表2 不同算法定位的仿真结果

从迭代次数看，无论是单个故障(T1～T2)，两个故障(T3～T4)，还是3个故障(T5～T6)，随着故障点的增多，3种算法的平均迭代数均增加，效率逐渐降低，但改进布谷鸟算法的平均迭代数最小，说明其定位效率最高，优于标准布谷鸟算法和AGA算法。

4 结束语

本文提出的改进布谷鸟算法无论是效率还是准确率都更具有优势，能准确定位配网故障，这是因为与标准布谷鸟算法相比，改进布谷鸟算法提高了算法的寻优性能，进而在一定程度提高了配网故障定位识别的准确率。但本文的改进只是从改变步长方面进行的，还可以从其他方面入手，因此未来研究还有较大的探索空间。