基于Petri网的购物储值卡流程模型优化
杨 璨,陶小燕
(安徽理工大学 数学与大数据学院,安徽 淮南 232001)
购物储值卡是现在常见的付款方式之一,一张购物储值卡可以拥有不同的面额.因在办理时通常采用不记名、不挂失的方式,所以持卡人在使用的时候会一旦丢失购物储值卡,则无法挂失,从而损失持卡人利益.为了能让持卡人在丢失卡的情况下利益不受到损害,构建购物储值卡模型,运用Petri网对购物储值卡进行业务流程建模,解决丢失卡情况下利益的保护问题.Petri网是在20世纪60年代由Petri发明的用来描述异步并发的计算机系统模型,越来越多的人使用Petri网这个工具建模.李巧丽[1]等调查了小商户的储值卡/会员卡使用现状,以及消费者对储值卡/会员卡使用的看法,深入研究其中存在的风险.何华莎[2]等调查了当下储值卡面临的一些情况,对于现在存在的问题提出了建议.本文针对购物储值卡无法实名和挂失、一旦丢失会损害持卡人利益的情况,基于Petri网提出一种优化模型,实现了购物储值卡的实名化和可挂失,方法具有适用性.
1 基本概念
定义1[3-5]满足以下条件的六元组N=(S,T;F,W,K,M)称作一个网:
(1)S∪T≠Ø;
(2)S∩T=Ø;
(3)F⊆(S×T)∪(T×S);
(4)dom(F)∪cod(F)=S∪T.其中,
(5)W∶S→{1,2,3,…}称为权函数,满足条件∀f∈F∶W(f)=1;
(6)K∶S→{1,2,3,…}称为容量函数,满足条件∀s∈S∶K(s)=∞;
(7)M∶S→{0,1,2,…}是∑的一个标识,满足条件∀s∈S∶M(s)≤K(s).
定义2[3](变迁发生规则)一个网系统(net system)是一个标识∑=(S,T;F,M)并具有下面的变迁发生规则(transition firing rule):
(1)对于变迁t∈T,如果∀s∈S∶s∈·t→M(s)≥1;

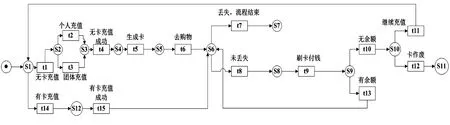
定义3[6](弱序关系)令(N,M0)是一个变迁集T上的网系统,其N=(P,T,F),弱序关系⊆T×T包含所有变迁对(x,y),存在一个发射序列=t1,∧,tn当>,j∈{1,∧,n-1},j (1)严格序关系→,当且仅当x>y,y≯x; (2)排他序关系+,当且仅当x≯y,y≯x; (3)交叉序关系‖,当且仅当x>y,y>x. 基于Petri网对购物储值卡建模,根据其内部结构优化分析购物储值卡流程模型.Petri网的运行规则能够反映在给定初始标识下流程模型的运行状态. 图1是现在市面上大多数储值卡使用的流程模型.当持卡人充值时可以选择使用已有的卡进行充值发生t14,或者充值新卡发生t1.持卡人只能选择一种方式办卡,所以t1和t14是排他关系,记作t1+t14.充值新卡有两种充值方式,即t2个人充值或者t3团体充值,t1和t2,t1和t3是严格序关系,记作t1→t2,t1→t3,持卡人只能选择一种方式,所以充值t2和t3是排他关系,记作t2+t3;发生t4无卡充值成功,接着发生t5生成卡,t4和t5是严格序关系,记作t4→t5;发生t6进行购物,t5和t6是严格序关系,记作t5→t6.持卡人在付款之前储值卡有两种状态,即t7卡丢失流程结束和t8卡未丢失继续购物,显然持卡人只能在两种状态中选择一种,所以t7和t8为排他关系,记作t7+t8.假如t8发生,发生t9刷卡付钱,t8与t9是严格序关系,记作t8→t9.发生t9之后,卡中余额出现两种状态,一种是t10无余额状态,一种是t13有余额状态,显然t10与t13只能发生一种,所以,t10与t13是排他关系,记作t10+t13.假如发生了t13,然后回到s6继续判断在刷卡前卡是否丢失.假如发生t10无余额状态,那么将会出现两种选择,一是t11继续充值,二是t12卡作废,显然t10与t11,t10与t12是严格序关系,t11与t12是排他序关系,记作t10→t11,t10→t12,t11+t12.如果选择t11,那么回到初始状态s1,假如选择t14之后,发生t15有卡充值成功,t14与t15为严格序关系,记作t14→t15.接着继续到s6,判断在刷卡之前卡有没有丢失.如果丢失发生t7卡丢失,流程结束. 在现实生活中,经常会发生卡丢失的状况.由于储值卡在办理的时不记名,不挂失,所以一旦丢失尤其是金额较大的储值卡损失非常大.笔者基于Petri网对图1的模型进行优化,优化后的模型见图2. 图1 优化之前的购物储值卡模型 在图2优化的模型中,引入了电子会员制度,且在t4无卡充值成功后,t5生成卡的同时系统中生成一个卡号,然后在s5进行一个选择,如果持卡人选择传统方式购物就发生t6,如果想要防止丢失就选择t16绑定电子会员购物,显然t6与t16是排他关系,记作t6+t16.持卡人选择t16之后进行一个选择,已有电子会员的话发生t17,如果没有电子会员就发生t18,t17与t18是排他关系,记作t17+t18;发生t19在电子会员中输入卡号,将储值卡与电子会员绑定.t17与t18分别与t19都是严格序关系,记作t17→t19,t18→t19.同样在s15做一个有没有丢失卡的判断.如果是t20未丢失,那么就直接发生t9刷卡付钱.但是如果t21丢失发生,那么持卡人就可以在电子会员中挂失,即发生t22.t21与t22是严格序关系,记作t21→t22;发生t23去前台补办,t22与t23是严格序关系,记作t22→t23;发生t9刷卡付钱. 图2 优化之后的购物储值卡模型,虚线框中为优化区域 优化模型一定程度上减小了丢失卡情况下的损失.同样,在t13储值卡有余额发生之后进行一个判断,在付款时储值卡是否与电子会员绑定.如果是t24未绑定的情况下,回到s5重新进行选择:是继续选用t6传统方式付款还是t16绑定电子会员方式付款.回到初始标识,如果选择t14有卡充值的话,发生了t15有卡充值成功之后进行一个选择,即有没有绑定电子会员.如果t26未绑定的话,转到s5可以重新选择是否绑定.如果是t27已经绑定的情况下,那么转到s15,同理在t9付款之前进行卡是否丢失的判断. 定义5[3](库所的有界性和安全性)设 ∑=(S,T;F,M0)为一个Petri网,s∈S.若存在正整数Z,使得∀M∈R(M0)∶M(s)≤Z:则称库所s为有界的(bounded),并称满足此条件的最小正整数Z为库所s的界,记为Z(s).即 当Z(s)=1时,称库所s为安全的(safe). 根据图2给出的优化后的购物储值卡Petri网模型,观察该Petri网,由于对各库所没有容量限制,在给定初始标识的情况下,变迁t1和t14都可以发生.通过观察其在Petri中的运行,可以求出各个库所的界为Z(s1)=Z(s2)=…=Z(s17)=1,存在Z=1.根据定义5,得出库所s1,...,s17都是安全且有界的结论. 用软件PIPE验证优化之后的模型,仿真结果表明,该优化之后的Petri网满足有界性和安全性. 本文针对购物储值卡无法实名和挂失、一旦丢失会损害持卡人利益的情况,基于Petri网提出一种优化模型,证明优化之后的模型满足有界性和安全性.PIPE软件的仿真验证结果表明,模型具有有界性与安全性,实现了购物储值卡的实名化和可挂失,本文的方法具有适用性.本文仅从控制流的角度进行分析,未来还需要在其他方面进行分析.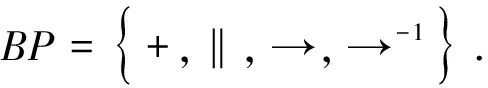
2 购物储值卡模型优化分析
2.1 构建购物储值卡流程模型分析
2.2 优化之后的流程模型分析
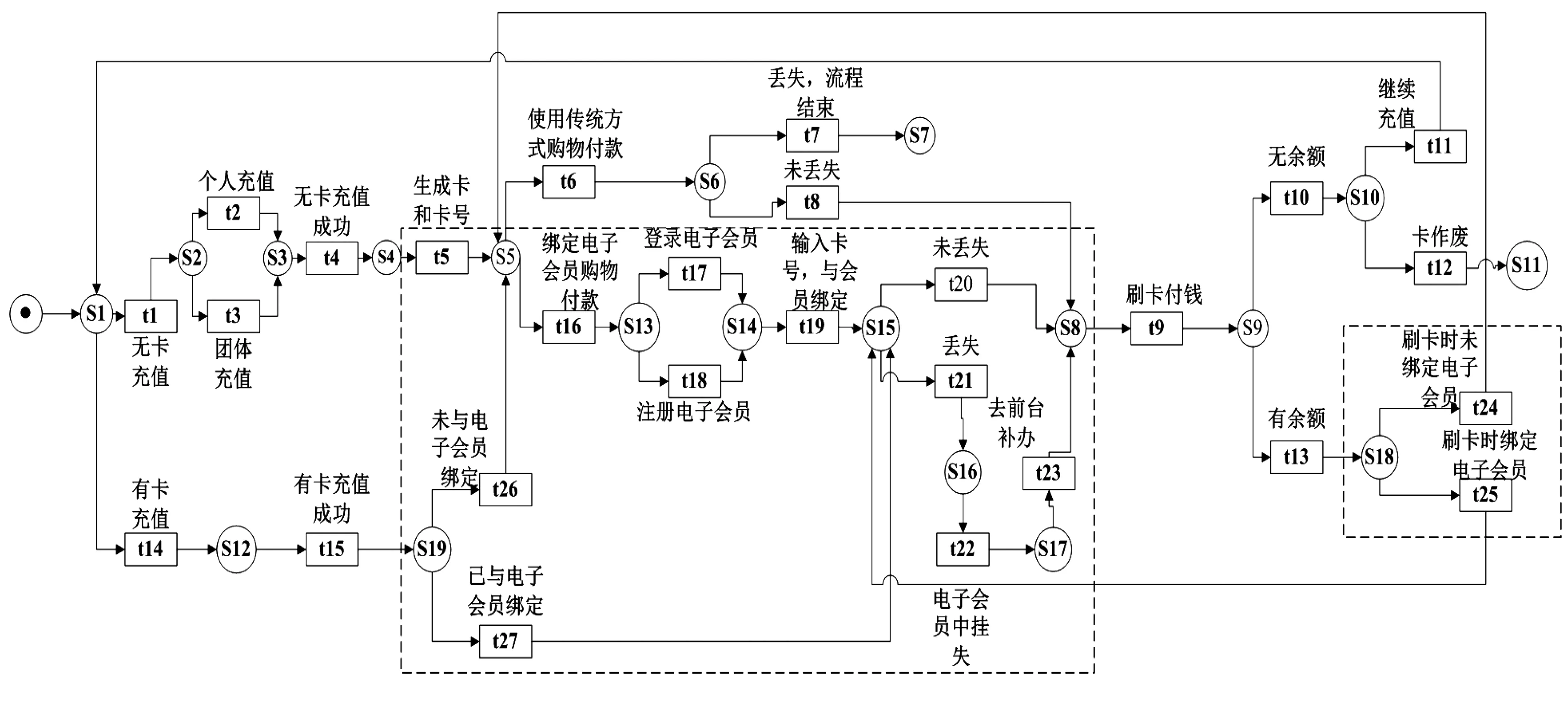
3 优化后模型Petri网的性质
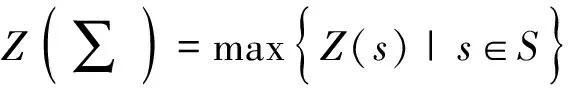
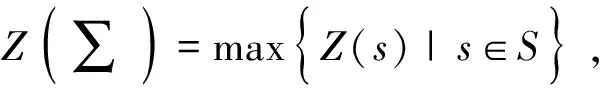
4 结束语
——以恶意透支信用卡诈骗为例

