二维半导体材料中激子对介电屏蔽效应的探测及其应用*

胡倩颖 许杨

1) (中国科学院物理研究所,北京 100190)

2) (南开大学物理科学学院,天津 300191)

二维过渡金属硫族化合物作为二维半导体材料领域研究的重要分支,凭借较强的光-物质相互作用和独特的自旋-谷锁定等特性,吸引了广泛而持久的关注.单层的二维过渡金属硫族化合物半导体具有直接带隙,在二维的极限下,由于介电屏蔽效应的减弱,电荷间的库仑相互作用得到了显著的增强,其光学性质主要由紧密束缚的电子-空穴对—激子主导.本文简单回顾了近年来二维过渡金属硫族化合物光谱学的研究历程,阐述了栅压和介电环境对激子的调制作用,之后重点介绍了一种新颖的激子探测方法.由于激发态激子(里德伯态)的玻尔半径远大于单原子层本身的厚度,电子-空穴对之间的电场线得以延伸到自身之外的其他材料中.这使得二维半导体材料的激子可以作为一种高效的量子探测器,感知周围材料中与介电函数相关的物理性质的变化.本文列举了单层WSe2 激子在探测石墨烯-氮化硼莫尔(moiré)超晶格势场引发的石墨烯二阶狄拉克点,以及WS2/WSe2 莫尔超晶格中分数填充的关联绝缘态中的应用.最后,本文展望了这种无损便捷、高空间分辨率、宽适用范围的激子探测方法在其他领域的潜在应用场景.

1 引言

自2004 年由Novoselov 等[1]在石墨中用机械剥离的方法分离出单原子层的石墨烯开始,二维材料由于具有方便易得的制备方法、独特的物理性质、多样的调控手段以及丰富的应用前景而激发起了广泛的研究兴趣.例如石墨烯就具有独特的无质量狄拉克费米子的色散关系[2,3],以及超高的电子迁移率[4],优秀的力学性能[5]和高热导率[6]等特性.由于石墨烯的零带隙特征限制了其在电子器件及光学等方面的应用,人们开始了对于具有本征半导体性质的二维材料的探索.作为二维半导体材料的代表,过渡金属硫族化合物(Transition metal dichalcogenides,TMDCs)可以与光发生直接而强烈的相互作用,带隙范围涵盖近红外到可见光波段,在光电子器件上有广阔的应用前景[7].此外,单层TMDCs 晶格本身的空间反演对称性破缺和自旋-谷锁定的特性,赋予了人们用光操控能谷自由度的可能,这种谷对比及其衍生的谷电子学,也使得TMDCs 成为近年来的研究热点[8,9].

当TMDCs 的厚度减小到原子层级别,除了间接带隙到直接带隙的能带结构转变外,还伴随着介电屏蔽效应的改变.单层二维半导体材料的光学性质由激子主导.这种由于长程的库仑相互作用结合而成的电子-空穴对,在二维极限下所受的介电屏蔽作用显著降低,电子-空穴对之间的相互作用(激子结合能)大大增强[10,11].激子的吸收光谱和发射光谱会受到电荷掺杂[12−14]和所处介电环境[15−17]的调制.因此可以利用该特点,将激子作为探测器,观测周围环境的物理性质变化.特别地,对于激发态的激子来说,其玻尔半径是单原子层厚度的数倍.这些电子-空穴对间的电场线广泛地延伸到周边的电介质中,可以对材料附近几纳米内的介电环境变化产生显著的响应,为二维材料中的量子态提供了一种新型的探测手段.

本文将介绍一种基于单层TMDCs 的激子探测方法.该方法利用上文提到的介电响应机制,将待测二维体系样品放置在与单层TMDCs 距离几纳米的范围内,通过一系列调控手段,使待测样品的物理性质发生变化(如电子态密度的变化、金属-绝缘体相变等),引发样品介电函数的改变.这种改变会影响TMDCs 中的库仑作用力,进而改变激子的束缚能及TMDCs 的带隙,并最终反映在TMDCs的光谱上.利用这种方法,可以灵敏地探测出石墨烯-氮化硼莫尔(moiré)超晶格势场引发的石墨烯二阶狄拉克点[18],以及WS2/WSe2莫尔超晶格中分数填充的关联绝缘态[19].相比其他测量方法,激子探测具有接近衍射极限的空间分辨率和不限定样品欧姆接触的广泛应用场景,可以便利地推广到其他材料体系,用简捷无损的光学方法实现对样品中与介电函数变化相关的物理过程的探测.

2 TMDCs 简介

对于TMDCs 的研究已有相当长的历史.早在1923 年,Dickinson 和Pauling[20]就首先给出了MoS2的晶体结构;19 世纪60 年代晚期,已有接近60 种TMDCs 被发现,其中大多都是层状结构[21];对MoS2的胶带法减薄,可追溯至1963 年[22];直到2004 年,单层石墨烯的成功解理以及一系列相关的技术,又为层状材料TMDCs 的研究带来了新的活力[1].特别是在2010 年,Splendiani 等[23]和Mak等[24]发现单层的MoS2是一种直接带隙半导体,使该体系收到了广泛关注.目前,对于最受关注的4 种二维半导体TMDCs(金属原子为Mo,W,硫族原子为S,Se),其直接带隙半导体的特征,以及独特的谷对比特性,使它们既可以作为基础科学研究的绝佳平台,又具备广阔的应用前景,本节将主要关注这几种TMDCs 的热力学稳定相,介绍它们的晶体结构及能带特征.

图1(a)展示了TMDCs 的3 种常见的晶体结构,分别对应着2H相、1T相和1T'相[10].单层的TMDCs 由3 个原子平面层(硫族元素-金属-硫族元素)构成.其中,2H相对应着ABA 堆叠次序,即不同层中的硫原子处于同一位置,上层的硫原子处于下层硫原子的正上方.1T相则具有ABC 的堆叠次序.而1T'相是由1T相晶格畸变造成.不同的晶格对称性决定了3 种相可以具有不同的物理性质.根据过渡金属原子和硫族原子种类的不同,TMDCs 有不同的热力学稳定相.对于常见的4 种TMDCs (MoS2,MoSe2,WS2和WSe2),其热力学稳定相一般为2H相.处于该相时,这4 种TMDCs都是半导体,能带结构也具有一定的相似性.

图1(b)展示了基于密度泛函理论计算的MoS2厚度依赖的能带结构[23],这种能带结构特征后续也被角分辨光电子能谱实验观测到[25].随着从块材减薄到单层,价带顶和导带底的位置不断改变,在单层的情况下,价带顶与导带底处于k空间的同一波矢上,具有相同的动量,由多层情况下的间接带隙半导体,演变成为直接带隙半导体.这种转变的一个显著表现就是单层MoS2的光致发光强度远强于双层和块材[24].图1(c)罗列了6 种常见的TMDCs 的能带排布[26],其光学带隙分布在红外至可见光波段[10,27],为常用波段的光电应用提供了可能.除了在发光器件和光探测器件上[28−30]的应用以外,在一系列新兴领域,如柔性光电器件[31]、可调激子器件[32]、量子点单光子源[33,34]中都有一定的前景.

TMDCs 能带结构中的另一个重要特点,赋予了它能谷依赖的物理性质.单层MoS2能带中的低能能谷分布于布里渊区两个不等价的高对称点,K点和K'点处,这种特征也存在于其他几种TMDCs和石墨烯中.然而石墨烯的对称性较高,在天然的情况下缺乏谷依赖的物理量,导致对谷的调控十分困难.与石墨烯不同,单层2H相的TMDCs 的A和B 子晶格分别由过渡金属和硫族两种原子占据,无需额外的掺杂或调控就天然地破坏了空间反演对称性,其价带和导带存在自旋-轨道耦合带来的自旋劈裂.这种劈裂在价带上尤为明显,例如MoS2的价带劈裂值约为150 meV,而WSe2的价带劈裂则达到了460 meV[35].时间反演对称性保证了在K点和K'点的自旋劈裂方向相反.以图1(d)中所画的MoS2为例,K谷的价带顶总是自旋向上,而K'谷的价带顶自旋向下,这种性质被称为自旋-谷锁定,即某一种谷总是对应着一种确定的自旋.在K和K'谷的带间跃迁符合手性光学选择定则.通过施加某一种旋性的圆偏振光,可以选择性地只激发其中的一个谷,实现对能谷自由度的有效调控.这种特性为利用谷自由度进行存储和运算提供了可能,是实现与自旋电子学相类比的谷电子学应用的基础[8,9].

图1 TMDCs 的结构和电子性质 (a) TMDCs 2H,1T,1T'相的晶体结构和层间堆叠序示意图;(b) 基于密度泛函理论计算的2H-MoS2 块材,四层、两层和单层的能带结构[23];(c) 6 种常见TMDCs 的能带排布[26];(d) 单层MoS2 的价带劈裂示意图,其中红色代表自旋向上,蓝色代表自旋向下;(e) TMDCs 中的激子示意图Fig.1.Structure and properties of TMDCs:(a) Atomic structure and stacking order of TMDCs in their trigonal prismatic (2H),distorted octahedral (1T) and dimerized (1T') phases;(b) calculated band structure evolution for 2H-MoS2 with decreasing thicknesses[23];(c) calculated band alignment between monolayer TMDCs[26];(d) schematic spin splitting of the bands at the K and K' points on the corners of the Brillouin zone of monolayer MoS2,where red and blue colors indicate up and down spin polarization,respectively;(e) schematic illustration of the exciton formation in TMDCs.

3 TMDCs 的激子光谱

作为一类半导体材料,当TMDCs 吸收一个光子,价带的电子就被激发到导带,而在价带留下一个空穴,如图1(e)所示,电子-空穴对之间由于库仑力相互吸引,形成束缚的电子-空穴对—激子.在通常的体材料中,由于电子-空穴对处于材料内部,所受的介电屏蔽作用很强,电子-空穴对之间的结合能较小.而在单原子层厚度的材料中,由于电子-空穴对之间的电场线延伸到周围的介电环境中,对库仑作用的屏蔽效应减弱,束缚显著增强.无论是前文中提到的大大增强的光发射[23,24],还是最近报道的接近百分之百的光吸收[36],都反映了单层TMDCs 在激子能量附近,光与物质之间强烈的相互作用.这为研究二维极限下的半导体光学性质提供了前所未有的平台.本节将沿着TMDCs 光谱研究的发展历程,重点介绍TMDCs 激子光谱中的层数依赖,谷光学选择定则,激子激发态及激子束缚能.

2010 年,Splendiani 等[23]和Mak 等[24]发现单层的MoS2是一种直接带隙半导体,这种直接带隙特征反映到光谱上,就对应着大幅提高的光致发光强度和量子产率.如图2(a)所示,单层MoS2的光致发光光谱由一个激子峰主导.当把单层MoS2的光致发光光谱与双层MoS2的发光光谱放在同一坐标系中对比时,会发现相比于单层的发光强度,双层的发光弱到可以忽略不计.插图中的曲线是不同层数的MoS2发光的量子产率,相较于块材,单层的量子产率大约高了4 个数量级.量子产率的提高源于间接带隙到直接带隙的转变,当价带顶与导带底处于k空间同一波矢位置,导带中的电子可以直接向价带跃迁,并释放出光子;而当导带顶与价带底在k空间不处于同一波矢位置时,由于动量守恒的需要,这种辐射跃迁过程还需要晶格振动(声子)等过程的参与,使得量子产率大幅度降低.图2(b)给出了不同层数的MoS2的光学带隙,即激子共振峰的能量.正如图1(b)显示的一样,随着层数增多,光学带隙逐渐变小,由单层的接近1.9 eV下降到块材的1.3 eV 左右,层数依赖的光致发光光谱很好地反映了MoS2能带结构的变化.类似的能带结构转变后续也在其他种类的TMDCs 中被发现[37].

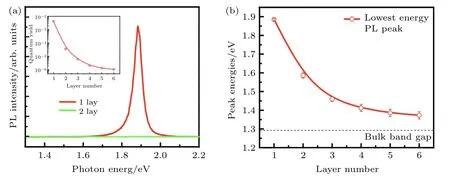
图2 层数依赖的MoS2 光致发光光谱[24] (a) 单层和双层MoS2 的光致发光光谱,插图是1—6 层MoS2 发光的量子产率;(b) 1—6 层MoS2 的激子共振峰(光学带隙)能量变化Fig.2.Thickness-dependent PL of MoS2[24]:(a) PL spectra for mono-and bilayer MoS2 samples,where the inset is PL quantum yield of MoS2 ranging from 1 to 6 layers;(b) energy variation of exciton resonance peak (optical band gap) energy of 1–6 layers of MoS2.

光对能谷的调控是TMDCs 最吸引人的特性之一.如图3(a)所示,2012 年Cao 等[38]和Xiao 等[39]预言,特定旋性的圆偏振光会选择性地激发K谷或K'谷之中的一个,进而产生谷对比.这种谷光学选择定则的第一个表现是,当给样品某一个旋性的圆偏振入射光,如果它只选择性地激发其中的一个谷,那么发射的光也应具有与入射光相同的旋性.图3(b)展示了用这种实验思路测得的光谱,用右旋圆偏振光作为入射光源,出射光中左右旋圆偏光所占的比例大不相同,大部分出射光都具有与入射光相同的旋性,体现出明显的谷对比特性,这种特性已被多个研究小组在实验上证实[40−42].在这种情况下,尽管两个谷会被某种旋性的偏振光选择性激发,两个谷的自旋遵循时间反演对称性,K谷和K'谷在能量上依旧是简并的.而当存在一个面外垂直磁场时,这种对称性就会被打破,两个谷之间将会存在图3(c)所展示的由塞曼效应导致的能量劈裂.这种劈裂带来了谷对比的第二个表现,外加磁场下左右旋圆偏光所对应的激子共振能量的不同.如图3(d)所示[43],在65 T 的垂直面外磁场下,左旋圆偏振光和右旋圆偏振光的激子共振峰相对零磁场下的共振峰分别向两侧偏移,偏移的程度与外加磁场的大小成正比[12].这种特性可以使人们将两个谷所对应的光学响应在能量上很好地区分开来.类似的行为也在其他种类的TMDCs 中被多个研究小组观测到,在磁场下都显示出了相似的谷对比特征[44−46].

图3 TMDCs 的谷光学选择定则 (a)零磁场下的能带示意图及谷光学选择定则[41];(b)谷对比的MoS2 偏振光致发光光谱;(c)面外垂直磁场下的能带示意图;(d)外加磁场下谷对比的WS2 反射谱[43]Fig.3.Optical selection rules of TMDCs:(a) Schematic illustrations of energy band and selection rules for valley-selective optical transitions at B=0;(b) polarized photoluminescence spectra of valley-contrasted MoS2 [41];(c) schematic diagram of the energy bands under the out-of-plane vertical magnetic field;(d) valley-contrast reflection contrast spectra of WS2 under external magnetic fields[43].

前文中所展示的TMDCs 反射谱和发光光谱,都是由一个明显的激子峰所主导.这个激子是价带顶的电子跃迁到导带底,并与价带顶的空穴由库仑作用力束缚在一起而形成的电子-空穴对.如图4(a)左侧插图所示,作为束缚的电子-空穴对,TMDCs中的激子能级可用氢原子模型来理解,其中n=1态对应激子的基态,n=2 及以上的态对应激子的激发态(因此也称为里伯德态)[11].图4(a)描绘了理想二维半导体的吸收光谱,由于电子-空穴间库仑相互作用的存在,激子的共振能量要低于准粒子带隙.为了与自由载流子所对应的准粒子带隙相区分,通常把光谱中能量最低的激子,即n=1 的基态激子共振峰能量称为光学带隙,这也是早期人们在实验中观测到的唯一一个激子共振峰.得益于样品质量的不断提高,更加高能量的激发态激子也陆续被实验观测到[47].图4(b)展示了实验测得的微分反射谱[48],从图4(b)可看到与图4(a)类似的激子激发态特征.这些激发态的能量更加接近准粒子带隙,激发态激子的共振强度以及相邻两激发态之间的能量间距随着n增大而减小.

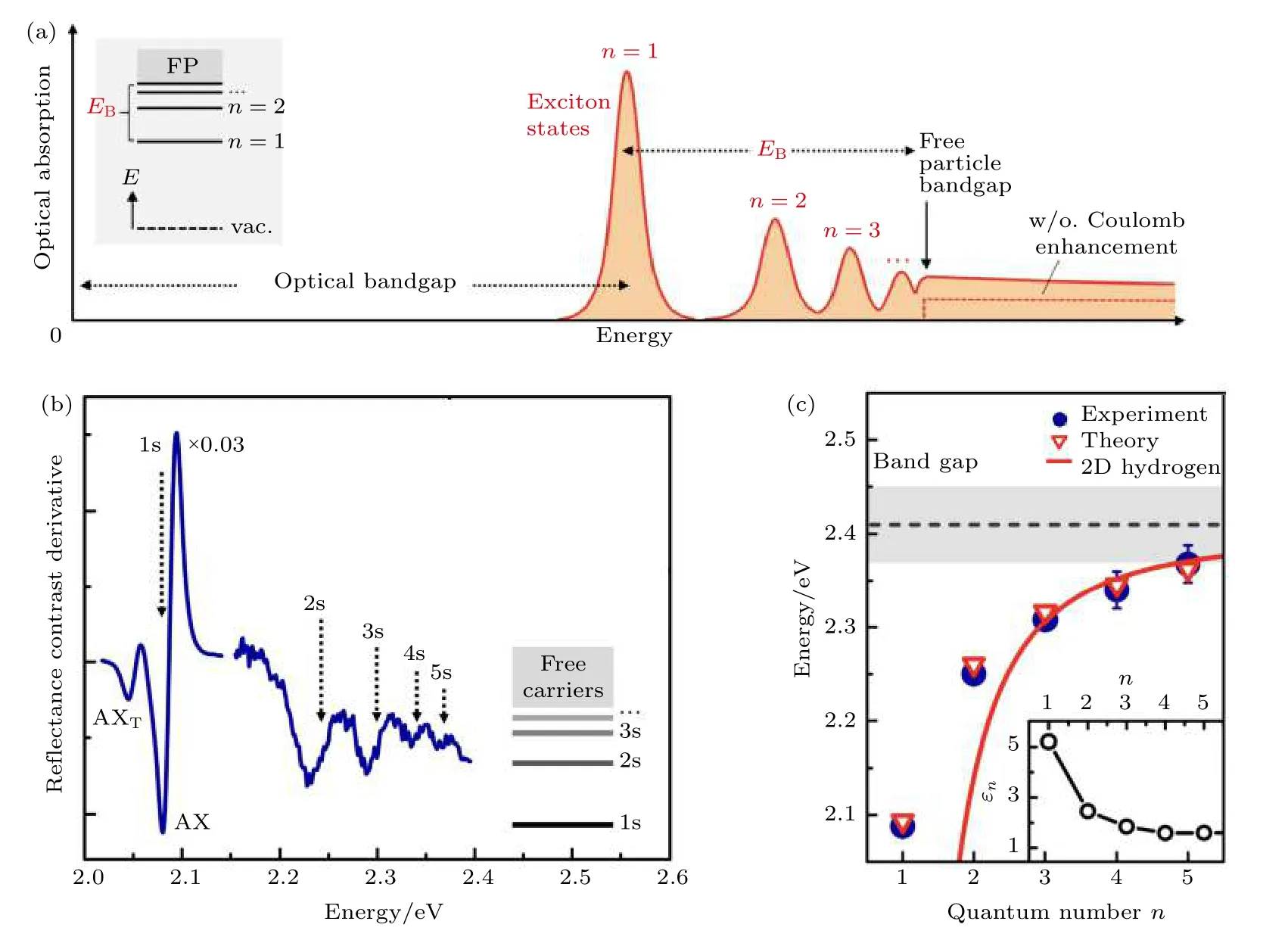
图4 TMDCs 的激子里德伯态 (a)理想二维半导体的光吸收示意图[11];(b)单层WS2 的微分反射谱[48];(c)实验及计算的WS2 激子里德伯态共振能量[48]Fig.4.Exciton Rydberg states of monolayer TMDCs:(a) Schematic illustration of light absorption of ideal 2D semiconductors[11];(b) reflection contrast derivative of monolayer WS2 [48];(c) experimentally extracted and calculated resonance energies of exciton Rydberg states[48].

激子束缚能是指激子共振峰与准粒子带隙之间的能量差,来源于导带电子和价带空穴束缚在一起的库仑作用能.相较于块材,二维TMDCs 具有非常大的激子束缚能,原因主要有以下几点:首先,维度的降低将所有的电子和空穴限制在只有几埃的平面内,这使他们之间的有效距离减小;其次,单层TMDs 的电子和空穴有效质量较大,在0.5 倍电子质量的量级;最后,由于三维到二维的转变,电子-空穴对之间的电场线得以广泛地延伸到面外的低介电常数的介质(如真空)中,介电屏蔽效应显著降低.测量激子束缚能的一种方法是用扫描隧道电子显微谱估测出准粒子带隙,再减去光谱测量中得到的激子共振峰能量[15].但这种方法较为繁琐,较简便的方法是将多个激子激发态的共振能量代入二维类氢原子模型,从而估计出激子束缚能.如图4(c)所示,从微分反射谱中提取出的激子共振能量与类氢原子模型估测的有一些偏差,尤其是对于n较小的情况[48].这是由于单层TMDCs 内部的介电常数远大于周边的介质,总的库仑相互作用势需要考虑这两种介电常数的综合作用.此时的势在电子-空穴间距很小的时候不再与距离成反比,转而与距离的对数成正比,可以用Keldysh 势来较为准确地描述.由于激发态激子的玻尔半径比基态的1s 激子大得多,大部分的电场线都延伸到了空气中,因此受TMDCs 自身介电函数的影响较小,更接近二维类氢原子模型描述的性质,等效的介电常数也小于1s 激子.另外,远大于材料自身厚度的玻尔半径,也使得激发态激子对材料附近的介电环境非常敏感,后文将阐述这种敏感性在激子探测上的应用.

4 栅压对TMDCs 光谱的调控

当一个半导体中掺入了多余的自由载流子,前文中所提到的激子将与这些自由载流子发生相互作用,这种相互作用在光谱上通常表现为激子共振峰位的移动和共振强度的增减.多余的自由载流子可能有多种来源,例如入射光提供的光生载流子,两种界面间的电荷转移,以及人为施加的栅压.本节将主要介绍栅压调控引入的自由载流子对于激子态的调控.

栅压调控的示意图如图5(a)所示.将电极与样品通过介电层隔开,将样品接地,在样品与电极之间施加一个栅压.此时该系统类似于一个平行板电容器,与电极所带电荷相反的自由载流子将由于两个平行板之间的电荷感应从地线注入样品中.早期研究认为,当掺杂多余载流子后,通过与自由载流子的非弹性散射,激子可以捕获额外的电荷,形成束缚的三粒子态,即带电激子/三子[13,14,49].与之相类似,两个激子也可结合在一起形成双激子态[50].而在近几年的研究中,Sidler 等[12]和Efimkin 等[51]认为这种三粒子或四粒子态仅适用于非常低的载流子浓度区间,当自由载流子浓度稍高时,极化子的物理图像更加合理.如图5(b)所示,当自由载流子注入到样品中后,原本的激子处于一个自由载流子组成的费米海的背景之中,费米海将与激子发生相互作用而偏离原本所在的位置,按照偏离的方向可以分为吸引极化子和排斥极化子两种情况,费米海的这两种偏离将对激子的行为产生不同的影响.图5(c)展示了按照这种图像计算的光电导谱.当考虑了费米海的作用时,光电导谱如图所示,分为了能量高的一支和能量低的一支,分别对应着排斥极化子和吸引极化子,图中虚线代表带隙的能量.图5(d)和图5(e)是实验测得的单层WSe2的光致发光光谱和反射谱.在栅压为零附近的区域,光谱由中性激子X0主导.在反射谱的中浓度电子/空穴掺杂区,可以观察到原本的中性激子发生蓝移,同时随着载流子浓度升高而逐渐消失,这就对应着能量较高的排斥极化子分支(RP).而在较高浓度的电子/空穴掺杂区,还出现了非常明显的红移支,即图中所标注的X+与X–,X–',这3 支与理论计算预测的吸引极化子(AP)分支行为类似.这种激子-极化子图像也可以理解为激子受到样品自身费米海的动态屏蔽效应,与栅压调控下的光谱特征较好地吻合,目前在学界受到了较为广泛的认可.

从图5 可以看到,光致发光光谱与反射谱之间存在一些明显的区别.其中,光致发光光谱反映的是被激发到高能级的电子跃迁回到低能级的过程,也称为辐射复合过程.然而由于样品中的缺陷和杂质散射的存在,为高能级到低能的跃迁提供了许多额外的非辐射复合通道,产生在低能量区的发光光谱上的杂峰,为研究样品的本征性质带来了干扰,如图5(d)中的发光光谱所示,这个效应在低温下会变的尤为明显.而反射谱所反映的是样品的光吸收过程,即低能级的电子吸收能量跃迁到高能级的过程,与弛豫过程无关.因此少量的杂质能级并不会对反射谱产生太大的影响.对于没有介电层影响的单层样品来说,反射谱近似地与样品的介电函数虚部(或光电导率的实部)成正比,即与光吸收成正比.当样品上下叠加了氮化硼封装层后,介电函数的实部也会对反射谱的峰形产生一定的影响.此外,反射谱还能有效捕捉带隙以上光学吸收过程,能够较为全面地探测材料的本征光学性质.

图5 栅压对二维激子的调控 (a)栅压调控的示意图;(b)吸引极化子和排斥极化子的示意图;(c)理论计算的忽略费米海(上)和考虑费米海(下)情况下的光导谱[51];(d)实验测得的1.6 K 下栅压调控的单层WSe2 光致发光光谱;(e)实验测得的1.6 K 下栅压调控的d 单层WSe2 反射谱Fig.5.Electrostatic charging effects of 2D excitons:(a) Schematic illustration of electrostatic gating;(b) schematic diagram of attractive polarons (AP) and repulsive polarons (RP);(c) calculated optical conductivity of excitons without (top panel) and within(bottom panel) Fermi sea[51];(d) photoluminescence (PL) of monolayer WSe2 as a function of gate voltage and photon energy at a temperature of 1.6 K;(e) reflection contrast of monolayer WSe2 as a function of gate voltage and photon energy at a temperature of 1.6 K.

5 TMDCs 光谱对介电环境的敏感性

前文中提到,由于激子的玻尔半径大于单原子层的厚度,电子-空穴对之间的电场线会延伸到原子层之外,这意味着激子会受到原子层之外的介电环境的影响.本节将介绍几种常见衬底上的单层TMDCs 光谱,以及同一衬底中变化的载流子浓度对TMDCs 光谱的调制.

对比以二氧化硅为衬底的和被两片氮化硼封装的MoSe2光致发光光谱时,会发现氮化硼的封装使得MoSe2光谱的线宽变小,发光峰变得更加锐利,这种对比在低温下更加明显[27],体现了氮化硼的封装对样品质量的提高.这主要有两个方面的原因.首先,在氮化硼封装的过程中,范德瓦耳斯力会使氮化硼和MoSe2紧紧吸附在一起,两种材料的一侧首先接触,之后在接触面不断增大的过程中,移动的接触线会将表面原本附着的部分污染物挤压出去.其次,相比于表面凹凸不平的二氧化硅,氮化硼的封装提供了一个原子级平整、没有悬空键、厚度均匀、介电常数一致的介电环境.这两种效应的结合,很大程度上避免了光谱的展宽,得到了质量更高的测试结果.图6(b)展示了没有覆盖双层石墨烯和覆盖了双层石墨烯的WS2的反射谱[16].就像图6(a)所描绘的那样,在覆盖了石墨烯的WS2中,由于石墨烯比空气的介电屏蔽能力更强,该区域的激子束缚能变得更小,电子-空穴对之间间距变大,同时WS2的带隙宽度也会受到介电环境的调制.从图6(b)可以看出,增加双层石墨烯后,激子共振峰的能量减小,说明带隙宽度减小量大于激子束缚能的减小量,最终使得激子共振峰红移.图6(c)总结了WS2的1s 和2s 激子能量间距对石墨烯的层数的依赖关系.随着叠加的石墨烯层数变多,1s 和2s 激子的能量间距减小,这也印证了激子束缚能随着石墨烯厚度增大而不断减小的趋势.图6(d)列举了处于几种常见的介电环境中,WS2的激子共振能量及激子束缚能,展示了介电环境对于单层TMDCs 激子光谱的显著调制.

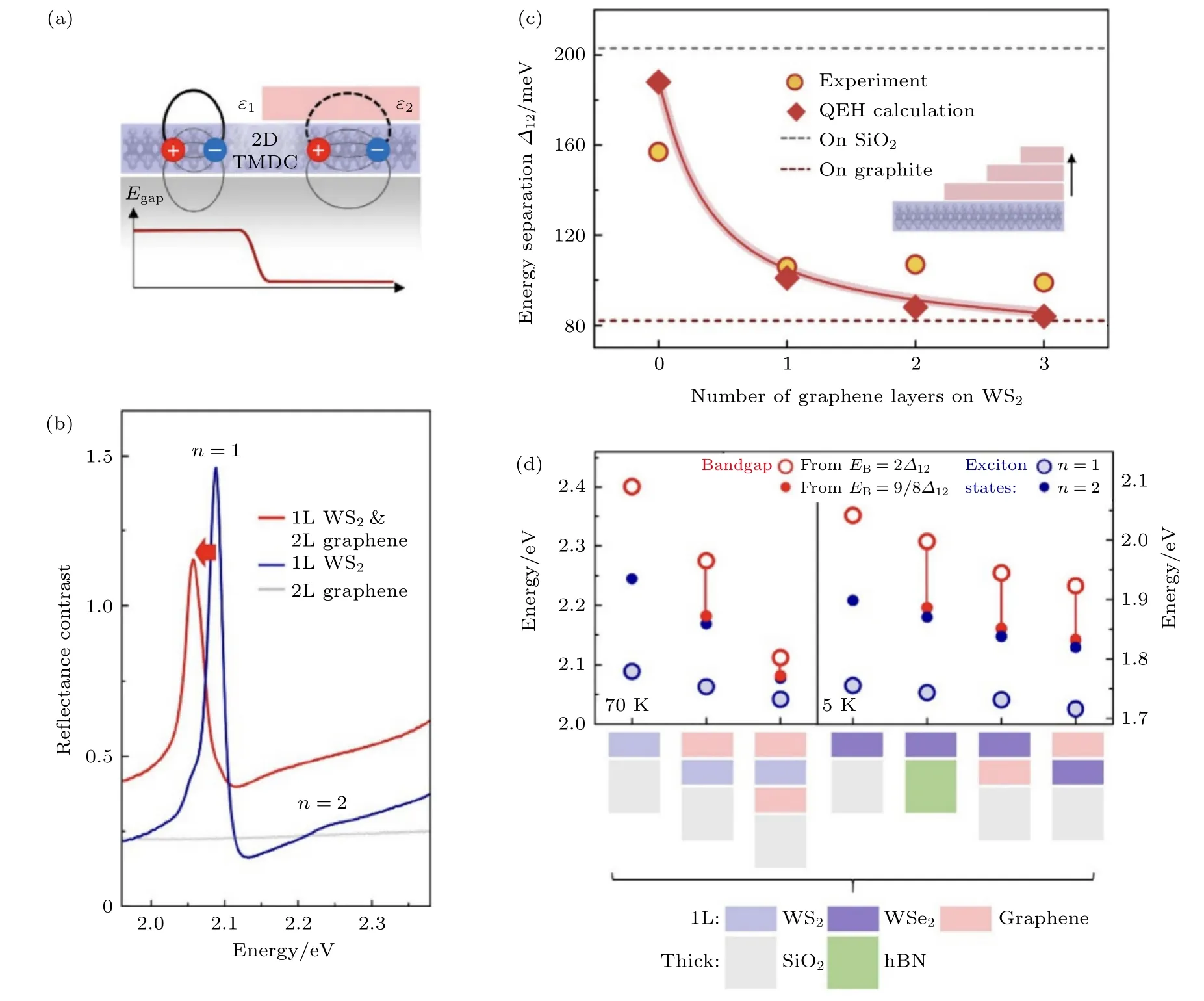
图6 TMDCs 在不同介电环境下的反射谱[16] (a)介电环境对二维TMDCs 带隙的调制示意图;(b)双层石墨烯对单层WS2 反射谱的调制;(c) 1s 和2s 激子能量间距与石墨烯层数的关系;(d)不同衬底组合下的1s 激子共振能量及激子束缚能Fig.6.Reflection contrast of TMDCs in different dielectric environment[16]:(a) Schematic illustration of bandgap renormalization of 2D TMDCs;(b) reflection contrast spectra of monolayer WS2 with and without the neighboring 2-layer-graphene;(c) energy separation between 1s and 2s excitons with increasing thickness of the neighboring graphene;(d) 1s resonance energy and exciton binding energy with different neighboring materials.

TMDCs 激子对介电环境的敏感性不仅体现在不同衬底之间,即便对于同种衬底,当衬底的状态发生改变,这种改变影响到衬底的介电函数时,TMDCs 的激子束缚能和带隙宽度也会受到显著的调制[17].图7 展示了不同栅压下的ReSe2-石墨烯的激子共振峰和准粒子带隙.需要注意的是,这里的栅压调控与第4 节所提到的栅压调控的效果完全不同.此处TMDCs 与石墨烯叠在一起,考虑这两种材料的能带结构排布,石墨烯的狄拉克点处于TMDCs 的带隙之中,所以当对ReSe2-石墨烯外加栅压时,无论流入的载流子是电子还是空穴,所有的载流子都会注入到石墨烯之中.而ReSe2始终保持电荷中性,载流子浓度不会被栅压所调控,栅压只改变它所处的介电环境.图7(a)给出了用扫描隧道谱测得的ReSe2价带顶和导带底随栅压的变化.值得一提的是,由于界面处的电荷转移,这里的石墨烯在外加栅压之前就是电子掺杂的,即栅压为零的时候载流子浓度不为0.对于这个样品来说,电荷中性点在–60 V 以下,因此,栅压从–60 V变为40 V 的过程,是石墨烯中自由电子浓度不断增高的过程.从图7(a)可看出,随着石墨烯电子浓度不断增高,ReSe2价带顶(VBM)和导带底(CBM)的能量都在降低,由于导带底降低得速度更快,ReSe2的准粒子带隙单调递减.图7(b)给出了不同栅压下,即石墨烯不同载流子浓度下,ReSe2的反射谱.与准粒子带隙展现出的栅压依赖不同,反射谱中的激子共振能量,即光学带隙,几乎保持不变.图7(c)总结了准粒子带隙、光学带隙与激子束缚能随栅压的变化,这种变化可以用图7(d)来定性地解释.随着石墨烯中的自由电子浓度不断增高,石墨烯的介电函数增大,对上方的ReSe2中激子的介电屏蔽作用增强,这使得ReSe2激子束缚能减小,电子-空穴对间距变大.与此同时,石墨烯介电函数的变化也调制了上方的ReSe2的能带,使准粒子带隙减小.对于图7(b)中所观测的1s 激子,激子束缚能的减小量恰好等于准粒子带隙的减小量,因此光谱中的1s 激子共振能量几乎保持不变.

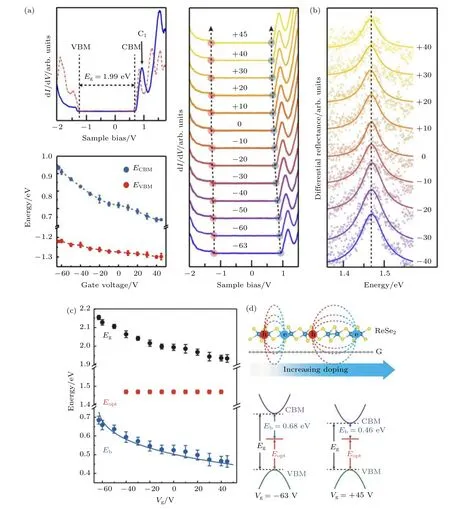
图7 动态介电屏蔽下的TMDCs[17] (a)扫描隧道谱测量的ReSe2 带隙随栅压的变化;(b) ReSe2 反射谱中随栅压几乎不变的激子共振能量;(c)扫描隧道谱测得的准粒子带隙(Eg),反射谱测得的光学带隙(Eopt)以及由此计算出的激子束缚能(Eb)随栅压的变化;(d)石墨烯不同掺杂程度下ReSe2 的激子和能带示意图Fig.7.TMDCs under dynamic screening[17]:(a) Bandgap evolution of ReSe2 with gate voltages obtained by scaning tunnelling spectroscopy;(b) nearly gate-independent exciton resonance energy of ReSe2;(c) evolution of bandgap (Eg),optical resonance energy(Eopt) and binding energy (Eb) with gate voltage;(d) schematic band structure of dynamically screened ReSe2 with the neighboring graphene at different doping levels.

6 基于TMDCs 激子的介电环境探测及其应用举例

考虑到第5 节中介绍的TMDCs 激子对介电环境变化的敏感性,Xu 等[19]设计了一种基于单层TMDCs 激子的介电环境探测方法.本节将简要介绍这种激子探测方法的原理,及其在探测石墨烯/氮化硼莫尔超晶格引发的石墨烯二阶狄拉克点[18],和WS2/WSe2莫尔超晶格中分数填充的关联绝缘态[19]中的应用.

莫尔超晶格是两层在角度或晶格常数上轻微失配的材料叠在一起后,所形成的周期比原本材料大的多的准周期性结构.这种简单的堆叠带来了更大的晶格尺寸以及对原本能带结构的显著调制,使该体系中涌现出非常规超导[52]、关联绝缘态[53−56]、量子磁性[57−59]、莫尔激子[60−62]等新奇的物理现象.但与此同时,对莫尔超晶格体系的探索也面临着许多挑战,例如小角度堆叠的样品中经常出现的样品性质在空间分布上的不均匀性[63−65],以及半导体莫尔超晶格中过大的接触电阻对电输运和扫描隧道谱学测量的限制等.这些阻碍引发了对原有探测手段的改进和对新测试方法的探索.

从图7 可以看到,ReSe2附近的石墨烯中载流子浓度的变化显著地调制了 ReSe2的准粒子带隙和激子束缚能.尽管这种调制可以通过结合扫描隧道谱和反射谱得到,但扫描隧道谱对所测样品有导电性的要求,且测试过程较为繁琐耗时.如果能够仅通过对TMDCs 激子的测量观察到这种调制,那么就可以用光学方法来快速便捷地探测介电环境的变化.对于激子的基态(1s)来说,介电环境的变化对于准粒子带隙的修正和其对结合能的修正几乎相同,使得1s 激子峰的能量保持不变,因此1s 激子共振能量无法直接反映出介电环境的变化.但对于激子的激发态(n>1)而言,其激子束缚能对介电常数的依赖关系与基态激子不同,激子激发态的束缚能变化并不会与带隙的变化相抵消,介电环境的变化会反映在激发态激子的共振能量上,可以用光学方法直接观测到.此外,由于激发态激子更大的玻尔半径,能够探测到附近几纳米范围内的介电函数变化.其中,2s 激子在共振强度和探测灵敏度上达到了一个较好的平衡,非常适合作为一种量子探测手段,感知周围材料中与介电函数有关的的物理量的变化.

如图8(a)所示,石墨烯/氮化硼异质结样品层被放置在单层WSe2探测器附近,通过底部的石墨电极可以调控石墨烯中的载流子浓度[18].由于WSe2激子的电子-空穴对之间的电场线穿过样品层,样品层的介电函数变化将反映在WSe2激子的共振能量上.图8(b)给出了石墨烯中载流子浓度的变化对WSe2反射谱的调制.与石墨烯-ReSe2类似,由于其能带排列,栅压调控注入的载流子会全部进入石墨烯中,而WSe2始终保持电中性.类似于图7 的结果,1s 激子的共振能量几乎不随栅压调控而变化.而能量更高的2s 激子随着载流子浓度的升高而发生显著的红移.在载流子浓度更高的区域,石墨烯中的载流子对激子的屏蔽效果大幅增强,2s 激子的束缚能急剧减小,2s 激子逐渐淹没在带边吸收中.图8(c)给出了从反射谱中提取的带隙宽度随栅压和载流子浓度的变化关系,高载流子浓度下的带隙宽度大致与载流子浓度的平方根成正比.由此可以看出,在该器件的调控范围内,WSe2的带隙变化量可以近似地正比于石墨烯中的电子态密度,这可能与石墨烯的介电函数在长波极限下正比于其电子态密度有关.而在石墨烯与氮化硼零度堆叠后,由于二者有轻微的晶格失配,形成了比原本晶格周期大得多的莫尔超晶格结构.这种周期性结构将给WSe2提供一个介电常数周期性变化的衬底,进而周期性地调控WSe2的带隙宽度.图8(d)展示了用WSe2激子探测石墨烯-氮化硼莫尔超晶格得到的栅压依赖的反射谱.当氮化硼与单层石墨烯形成了莫尔超晶格后,光谱在空穴掺杂区出现了一个新的类似于电中性的单层石墨烯狄拉克点处的特征,以及两条更高能量的伴线,这两种特征都来源于超晶格的作用.首先,在石墨烯-氮化硼的莫尔超晶格势场的作用下,石墨烯的能带结构由于AB 子晶格对称性被打破,在价带打开了一个二阶狄拉克点.这个位置的电子态密度变小,使得介电屏蔽效应减弱,WSe2带隙蓝移[66].其次,超晶格势场使WSe2中产生了新的被允许的光学跃迁,两支伴线对应着WSe2迷你布里渊区边界M点和K点的跃迁.

图8 石墨烯-氮化硼异质结的激子探测[18] (a) WSe2 激子探测石墨烯-氮化硼莫尔超晶格的器件结构(上),探测原理示意图(中)及周期性衬底对WSe2 带隙宽度的调控(下)示意图;(b) 石墨烯中载流子浓度变化对WSe2 反射谱的调制;(c) 图(b)中的带隙能量与栅压和载流子浓度平方根(插图)的关系;(d) 当石墨烯与上层氮化硼零度排列形成莫尔超晶格时,石墨烯中载流子浓度变化对WSe2 反射谱的调制;(e) 石墨烯二阶狄拉克点(左)和伴线(右)的来源示意图Fig.8.Dielectric sensing of graphene/hBN heterostructures[18]:(a) Device structure of the graphene/hBN heterostructure with WSe2 dielectric sensor (top),illustration of creating spatially periodic electronic band structure in monolayer WSe2 by dielectric screening(middle),and bandgap (Eg) of WSe2 modulated by a substrate with periodic dielectric constant (bottom);(b) gate-dependent reflection contrast spectrum of WSe2 sensor under dynamic screening of the neighboring graphene;(c) the extracted quasiparticle band gap Eg of monolayer WSe2 in (b);(d) gate-dependent reflection contrast spectrum of WSe2 sensor with graphene/hBN moiré superlattice;(e) origin of the secondary Dirac point (left panel) and replicas (right panel) in (d).

图9 展示了利用激子激发态探测到的二维半导体WSe2/WS2莫尔超晶格中丰富的关联绝缘态[19],器件结构示意见图9(a).待测样品是WSe2/WS2,探测器是一层单独的WSe2.探测器与样品层分别接地,且探测器与样品之间用氮化硼隔开.由于探测层和样品都是TMDCs,不具备TMDCs/石墨烯的能带排列,如果不隔开样品层和探测层,无法保证探测层始终处于电中性的状态,样品与探测层之间的相互作用也可能会使测到的光谱无法独立反映样品的性质.将样品层接地后,通过调节顶电极的栅压,可以调控样品中的载流子浓度,将探测层接地,底电极也接地,就可以保持探测层始终处于电中性,这样探测层的光学响应随栅压的变化,所反映的就是样品层介电函数的变化.图9(b)和图9(c)给出了没有探测层的区域和有探测层的区域的反射谱.1.65—1.70 eV 的信号来源于样品层的激子共振峰,而1.72—1.85 eV 是探测层的1s与2s 激子共振峰.探测层的2s 展现出了一系列的精细特征,反映了样品层随栅压变化而变化的介电函数.图9(d)放大了图9(c)中2s 激子的精细结构,可以发现,这些特征的出现是由于某一些栅压值所对应的激子共振峰发生了蓝移和增强.在某些特定的栅压值所对应的载流子浓度下,每一个莫尔超晶格恰好被整数或分数个电子/空穴填充,这个数字称为填充数.填充数为2 时,每个超晶格填充的电子恰好填满迷你布里渊区能量最低的子带,因此出现一个绝缘态,对应平庸的能带绝缘体.填充数为1时,子带被半填充,即每个超晶格中填充一个电子,由于在位(on-site)电子间的强库仑排斥作用占主导,出现了莫特绝缘态.而在某些特定分数填充时(如1/2,1/3,1/4 等),电子与电子之间的相互作用由位间(inter-site)的库仑相互作用主导,自发地按照总库仑势最低的方式排列,如图9(e)所展示的几种情况.此时的电子波函数被局域化在相应的格点上,破坏了超晶格本身的平移对称性,形成了电荷密度波,也被称为广义的维格纳晶体[54,55,67].这种电子相互作用产生的在特定载流子浓度下的关联绝缘态,降低了样品的介电函数,改变了探测层激子的束缚能和带隙,进而反映在探测层的光谱上,使得2s 激子在这些载流子浓度下发生蓝移和共振强度的增强.与此同时,该方法还可用于确定不同关联绝缘态的相变温度,相变温度与2s 的峰位移动显示出正相关的特性,反映了不同分数填充态的能量关系.此后,这些分数填充态也被其他研究小组通过扫描微波显微术探测局部微波阻抗[68]和光致发光谱的方法探测到[69].从图9(e)可以看到,样品层本身的莫尔激子(1.6—1.7 eV)也在整数填充和某些分数填充的位置体现出了强弱或峰位的变化,但相比之下,探测层2s 激子的变化特征要清晰和锋利许多.同时,莫尔激子本身和费米海中载流子的相互作用也较为复杂和难以理解.因此,探测层的加入对于分数填充关联绝缘态的探测依旧是十分必要的.

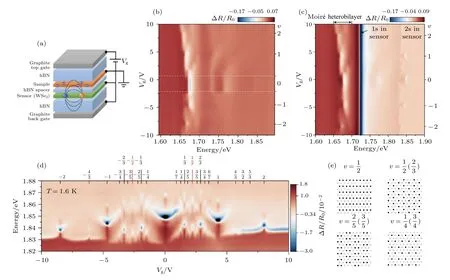
图9 WSe2/WS2 莫尔超晶格的激子探测[19] (a) WSe2 激子探测WSe2/WS2 样品的器件结构示意图;(b)在没有WSe2 探测层的区域,WSe2/WS2 样品自身的反射谱;(c)有WSe2 探测层区域的反射谱;(d)图(c)中2s 区域体现出的一系列关联绝缘态;(e)几种分数填充的示意图Fig.9.Dielectric sensing of WSe2/WS2 moiré superlattice[19]:(a) Device structure and electric circuitry of the WSe2/WS2 moiré heterobilayer with WSe2 dielectric sensor;(b) optical response of the WSe2/WS2 moiré heterobilayer without WSe2 dielectric sensor;(c) optical response of the WSe2/WS2 moiré heterobilayer and WSe2 sensor;(d) abundance of correlated insulating states in WSe2/WS2 moiré heterobilayer revealed by 2s resonance of WSe2;(e) schematic illustration of charge-order configuration in correlated insulating states.

7 激子探测法的总结与展望

本文简单回顾了与TMDCs 中激子相关的光谱学研究的发展历程,重点介绍了单层TMDCs中的激子受到介电屏蔽效应的调制作用.这种介电屏蔽效应的调制可以来自于样品本身的掺杂改变(通过施加栅压)或是周围材料介电环境的变化.后者提供了一种基于单层TMDCs 激子的介电环境探测方法,文中介绍了几个利用这种方法来研究与莫尔超晶格相关的物理现象的应用实例.最后,本节将简要总结这种激子探测方法的优势,及其在探测其他体系和其他物理现象中的潜在应用.

首先,激子探测方法是针对TMDCs 探测层的光学测量,并不是直接探测样品层,而是通过TMDCs 探测层光学响应受样品层的调制,来反映样品层中的介电常数变化.这种测量光强低(一般等于或小于纳瓦量级),对样品层的扰动和破坏非常小,可以得到样品本征的、低能的性质.该方法继承了光学测量的简便性和快捷性,测试手段常规,不需要额外的测量技术.其次,激子探测方法具有接近衍射极限的空间分辨率,在空间分布不均匀的样品中也依旧适用.以莫尔超晶格样品为例,小角度堆叠的样品中常常会存在超晶格周期在空间分布上的不均匀[63−65].对于传统电学输运测量,测得的是整个样品区域的平均信号,如果样品空间分布不均,从不同区域测到的不同信号会叠加在一起,对分析处理数据产生干扰.而激子探测的方法在一定程度上避免了这一问题.入射光斑的大小可以很容易地达到1 µm 左右,不仅可以测量到样品中各个区域的独立的信号,还可以通过比较不同区域内信号的差别,对这种空间不均匀性进行表征.最后,激子探测的适用范围非常宽,这种宽范围表现为:1)它是一种光学测量,但探测的样品并不局限于与光相互作用较强的半导体;2)它能探测到与输运相关的费米面附近的电子态密度的信息,但又不像输运测量那样对样品导电性有较高的要求;3)它能探测到样品介电函数的变化,而不局限于电子态密度的变化,凡是能改变样品介电函数的物理量的过程(如金属绝缘体相变,乃至超导转变等),都可能被探测层感知.这是由于对于激子的屏蔽效应并不完全是静态的,需要考虑到介电函数中一定频率范围内带内和带间跃迁的贡献.总的来说,这种激子探测方法结合了光学测量与输运测量的优势,无损便捷,空间分辨率高,测试范围广,可以推广到更多的材料体系和物态变化的测量中去.

但同时也需要认识到,对于该测量方法理论模型的构建还不完善,很难从实验中直接提取与待测系统相关的定量的物理信息.要建立起一套统一的理论模型,就需要考虑到:1)探测层激子受到附近样品层费米海的动态屏蔽效应;2)二维半导体中的准粒子带隙受非局域化的屏蔽效应的影响;3)探测层和样品层间距的变化对于测量的结果的影响.与此同时,对于样品中发生的多体相互作用(如激子-极化子)和激子受到单纯的介电屏蔽效应如何理解与区分也是理论工作需要关注的内容.因此无论是在实验或是理论方面,都有很多具体的工作可以开展,我们期待能够看到这一领域的蓬勃发展.